Similar presentations:
Теорема об изменении момента количества движения
1.
Новосибирский Государственный Архитектурно-СтроительныйУниверситет (Сибстрин)
ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.
ДИНАМИКА
ЛЕКЦИЯ 5.
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
МОМЕНТА КОЛИЧЕСТВА
ДВИЖЕНИЯ
Кафедра теоретической механики
2. 1. План лекции
Введение1 Момент количества движения точки и механической
системы
2 Теорема об изменении момента количества движения
(теорема моментов)
3 ДУ движения твердого тела
4 Законы сохранения момента количества движения
5 Движение точки под действием центральной силы
6 Физический маятник
7 Решение задач с использованием теоремы моментов
Заключение
3. 2. На предыдущей лекции
Изучили первые две теоремы:- Теорему о движении центра масс
- Теорему об изменении импульса
Дали рекомендации к решению задач на применение
общих теорем динамики
Рассмотрели примеры решения задач
4. 3. Цель лекции
Изучить теорему об изменениимомента количества движения
механической системы (теорему
моментов)
5. 4. Введение
НАПОМНИМ: МЕРЫ ДВИЖЕНИЯ1 – центр масс системы
rC ( mk rk ) / M
2 – количество движения (импульс) системы
Q mk v k
3 – момент количества движения
(момент импульса) системы
KO M O (mk v k )
4 – кинетическая энергия системы
1
2
T ( mk v k )
2
6. 5. Введение
Напомним:Движение механической системы мы будем
изучать по поведению ее характеристик (мер
движения) - центра масс, количества
движения, момента количества движения,
кинетической энергии
Поведение же этих характеристик будет
определяться теоремами об их изменении со
временем.
На этой лекции мы изучим третью теорему:
Теорему об изменении момента количества
движения
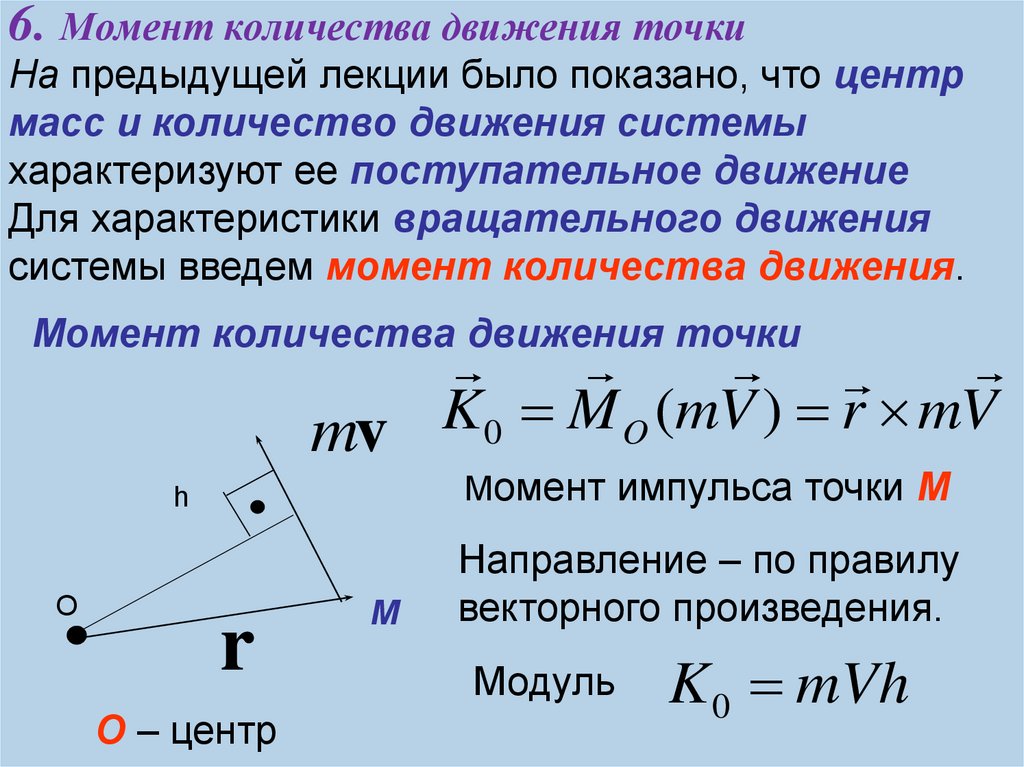
7. 6. Момент количества движения точки
На предыдущей лекции было показано, что центрмасс и количество движения системы
характеризуют ее поступательное движение
Для характеристики вращательного движения
системы введем момент количества движения.
Момент количества движения точки
K
M
(
m
V
)
r
m
V
0
O
mv
Момент импульса точки M
h
O
r
O – центр
M
Направление – по правилу
векторного произведения.
Модуль
K 0 mVh
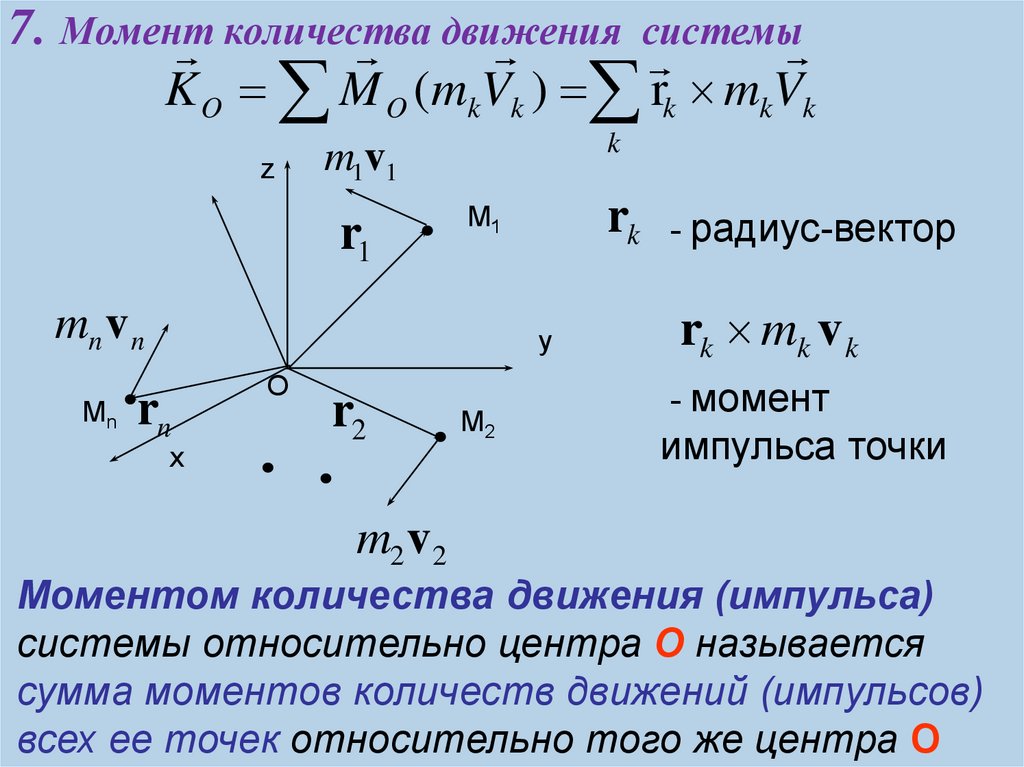
8. 7. Момент количества движения системы
K O M O (mkVk ) rk mkVkz
k
m1v1
r1
mn v n
Mn
rk - радиус-вектор
M1
y
rn
O
r2
x
M2
rk mk v k
- момент
импульса точки
m2 v2
Моментом количества движения (импульса)
системы относительно центра О называется
сумма моментов количеств движений (импульсов)
всех ее точек относительно того же центра O
9. 8. Проекции момента импульса
K 0 rk mk v k(1)
k
K x mk ( y k v kz z k v ky )
k
K y mk ( z k v kx xk v kz )
(2)
k
K z mk ( xk v ky y k v kx )
k
x k , y k , z k - координаты точек M k , k 1,..., N
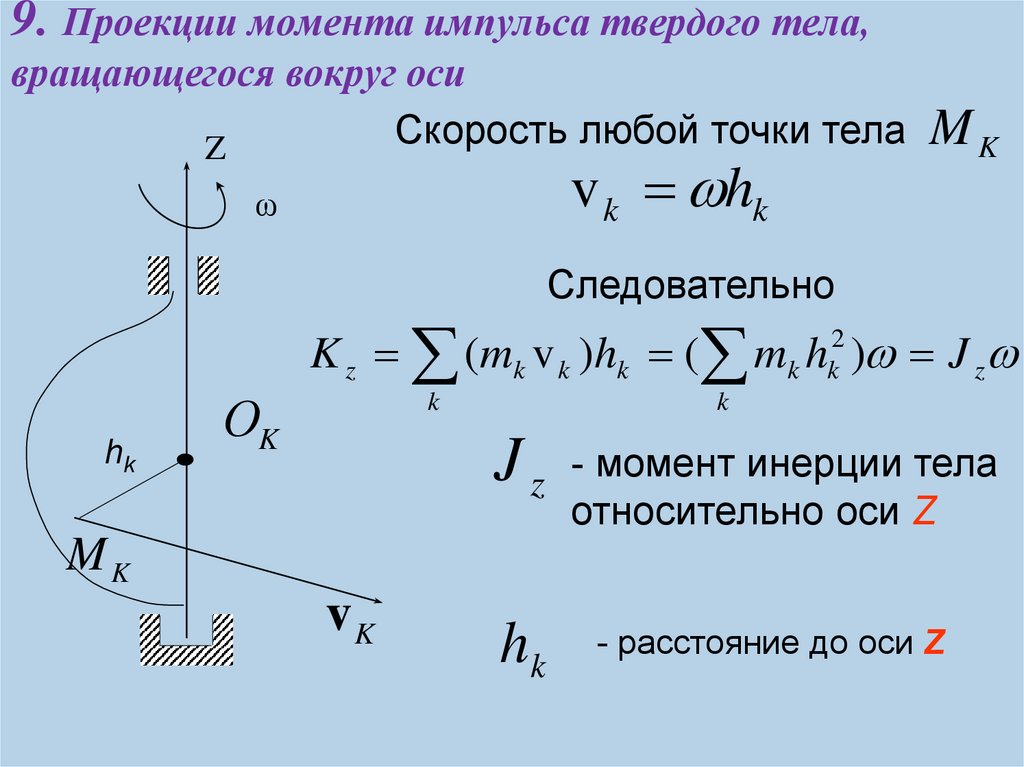
10. 9. Проекции момента импульса твердого тела, вращающегося вокруг оси
Скорость любой точки тела M KZ
v k hk
ω
Следовательно
hk
ОK
K z (mk v k )hk ( mk hk2 ) J z
k
k
J z - момент инерции тела
относительно оси Z
MK
vK
hk
- расстояние до оси Z
11. 10. Проекции момента импульса твердого тела, вращающегося вокруг оси
v kz 0,v ky xk ,
- проекции скорости точки тела
v kx yk
Следовательно
K x mk ( y k v kz z k v ky ) ( mk xk z k ) J xz
k
k
K y mk ( z k v kx xk v kz ) ( mk y k z k ) J yz
k
J xz , J yz
k
- центробежные моменты инерции тела
12. 11. Проекции момента импульса твердого тела, вращающегося вокруг оси
Для вращающегося вокруг оси Z твердого телаего моменты импульса относительно осей X,Y,Z
K 0 (K x , K y , K z )
K x J xz
K y J yz
(3)
K z J z
Чтобы K 0 был направлен вдоль Z
необходимо и достаточно, чтобы его центробежные
моменты инерции были равны нулю
(например, Z - ось симметрии тела)
13.
12.Аналогия между поступательным и
вращательным движением
для поступательного движения мерой его
движения является количество движения
Q (Q x , Q y , Q z )
для вращательного движения мерой движения
(мерой вращения) является его момент
количества движения
K 0 (K x , K y , K z )
14.
13. Если твердое тело движется поступательно, тоего момент импульса относительно центра O
K 0 rk mk v k ( mk rk ) v Mrc v rc ( Mv)
k
k
при определении момента импульса его можно
считать точкой, расположенной в центре масс
Момент количеств движения системы
относительно разных точек A и B
K B K A BA ( Mv C )
аналогична формуле из статики
M B M A BA R
*
R * - главный вектор
15. 14. Теорема моментов
dv ke
i
mk
Fk Fk , k 1,..., N
dt
(4)
умножим обе части уравнений векторно на
rk
dv k
e
i
rk (mk
) rk Fk rk Fk
dt
левая часть
dv k
d
rk (mk
) (rk mk v k ) v k mk v k
dt
dt
16. 15. Теорема моментов
Т. к. векторыv k и mk v k
параллельны, то
v k mk v k 0
мы получаем
d
e
i
(rk mk v k ) rk Fk rk Fk
dt
суммируем
k
d
(rk mk v k ) rk Fke rk Fki
dt
k
k
(5)
17. 16. Теорема моментов
r F 0По свойству внутренних сил
k
i
k
k
Учитывая, что сумма производных равна
производной от суммы, получаем
d
(rk mk v k )
dt k
r F
k
e
k
k
или
dK 0
e
M 0 (Fk )
dt
k
теорема моментов
(6)
18. 17. Теорема моментов
dK 0M 0 (Fke )
dt
k
(6)
Производная по времени от момента импульса
механической системы относительно некоторого
неподвижного центра О равна сумме моментов
всех внешних сил, действующих на эту систему
относительно того же центра О
Теорема моментов, также как и теоремы о
движении центра масс и об изменении
количества движения, позволяет исключить из
рассмотрения все наперед неизвестные
внутренние силы.
19. 18. Теорема моментов в проекциях на оси
dK xe
M x (Fk )
dt
k
dK y
e
M y (Fk )
dt
k
dK z
e
M z (Fk )
dt
k
(7)
20. 19. Д.У. вращательного движения твердого тела
dK ze
M z (Fk )
dt
k
K z J z
(7)
J z M z (F )
e
k
k
или
e
J z M z (Fk )
(8)
k
ДУ вращательного движения твердого тела,
Начальные условия:
(0) 0 , (0) 0
21. 20. Д.У. плоского движения твердого тела
Вспомним кинематику: Плоское (илипроизвольное) движения твердого тела мы
можем представить как сумму
поступательного движения вместе с центром
масс C и вращательного (или сферического)
движения вокруг центра масс C
Поступательная часть движения определяется
теоремой о движении центра масс
Ma c F
e
k
(9)
k
Для определения вращательной части движения
найдем выражение для теоремы моментов во
вспомогательной системе координат Cx1 y1 z1
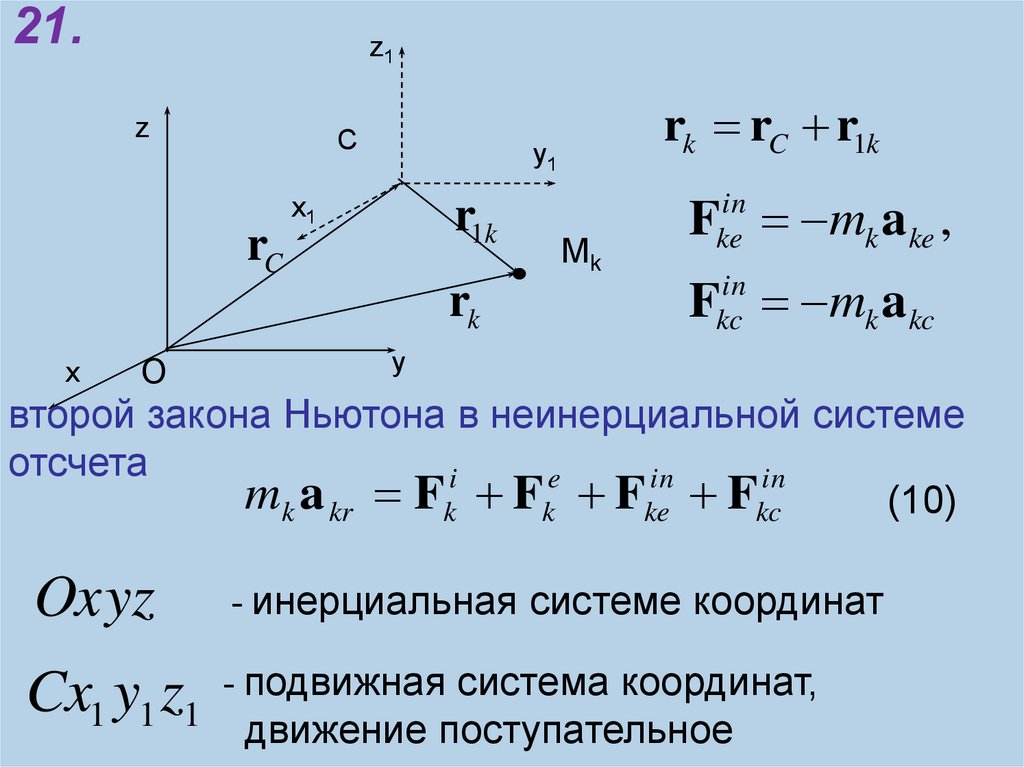
22.
21.z1
z
C
rC
y1
x1
r1k
rk
x
O
rk rC r1k
Mk
F mk a ke ,
in
ke
F mk a kc
in
kc
y
второй закона Ньютона в неинерциальной системе
отсчета
i
e
in
in
mk a kr Fk Fk Fke Fkc
(10)
Oxyz
- инерциальная системе координат
Cx1 y1 z1 - подвижная система координат,
движение поступательное
23.
e 022. Имеем:
M (F ) 0
0
i
k
F 0
in
kc
- по свойству внутренних сил
k
Повторяя те же выкладки, что были при
выводе теоремы моментов, получим
dK c
M c (Fke ) M c (Fkein )
dt
k
k
(11)
K c вычисляется в системе координат Cx1 y1 z1
a ke a c - для всех точек; F mk a ke mk a c
in
ke
in
M
(
F
C ke ) ( mk r1k ) aC Mr1C aC 0,
k
т.к. r1C 0
k
24.
23.В результате мы получили
dK c
e
M c (Fk )
dt
k
(12)
В системе координат, движущейся поступательно
вместе с центром масс, теорема моментов
относительно центра масс сохраняет тот же вид,
что и относительно неподвижного центра
25.
24.Д.У. плоского движения твердого тела:
M x c F
e
kx
k
M y c F
e
ky
(13)
k
J c M c (F )
e
k
k
при начальных условиях
xc (0) xc 0 , yc (0) yc 0 , (0) 0 ,
x (0) v Cxo , y (0) v Cyo , (0) o
26. 25. Законы сохранения момента импульса
1. Пусть сумма моментов внешних сил равнанулю
e
M
(
F
0 k) 0
k
Тогда из уравнения
dK 0
M 0 (Fke )
dt
k
K 0 const (14)
следует
Если сумма моментов внешних сил относительно
О, действующих на механическую систему равна
нулю, то момент импульса сохраняется во все
время движения
27. 26. Законы сохранения момента импульса
2. Если сумма моментов всех внешних сил,действующих на систему относительно
e
некоторой оси равна нулю
M (F ) 0
z
k
k
то момент количества движения относительно
этой оси сохраняется
K const (15)
z
Для вращающегося тела формула (15) дает:
J z const
Примеры: вращение фигуриста, сальто гимнаста,
падение человека – руки расставляет, падающая
кошка приземляется на ноги!
28. 27. Физический маятник
С - центр масс; OC aR0
J0
O
φ
mg
- момент инерции
относительно оси O
e
dK O
M O ( Fk )
dt
C
K
J 0 mga sin
k sin 0; k 2 mga / J 0
2
Получили нелинейное ДУ.
Ограничимся случаем малых колебаний
29.
28. Случай малых колебаний2
k 0
sin
cos 1
A sin( kt )
НУ:
t 0, (0) 0 , (0) (0) 0
A (v0 / k )
2
0
2
arctg ( 0 k / 0 )
Период колебаний: TФ 2 / k 2
J 0 / mga (17)
(не зависит от начальных условий)
Из (17) следует:
J 0 mgaT / 4
2
Ф
2
(18)
Формулу (18) используют для опытного
определения J 0
30. 29. Движение Земли вокруг Солнца
М– Земля, О - Солнце
F – сила притяжения
Земли
к
Солнцу
S
M(t+Δt)
z
M(t)
O
F
y
dK 0
M O ( Fke ) 0
dt
K
r
m
V
const
O
K O r mV m lim( r r / t )
x
m lim( 2 S / t ) 2mS const S const
Радиус-вектор описывает равные площади в любые
одинаковые промежутки времени (закон площадей)
Из постоянства направления K
следует, что
O
траектория движения является плоской кривой
31. 30. Применение теоремы к установившемуся движению жидкости
V0b
C0
a
b1
a1
V1
z
O
y
x
d
с
d1
C1
c1
K 20 K10 K cdc1d1 K aba1b1 rс1 (mcdc1d1V1 ) rc0 (maba1b1V0 )
maba1b1 mcdc1d1 Gcek t K 20 K10 Gcek (rc1 V1 rc0 V0 ) t
e
t 0 Gcek (rc V1 rc V0 ) M O ( Fk ) (19)
1
0
Разность секундных моментов импульса относительно центра О, протекающих через два поперечных
сечения трубы, равна сумме моментов всех внешних
сил, действующих на объем жидкости, ограниченной
этими сечениями, относительно того же центра О
32.
31. Определим с помощьюV1
(19) момент M oz на ось
турбины сил давления воды.
e
Gcek (rc1 V1 rc0 V0 ) M O ( Fk ) (19)
R1
α2
α1
V2
R2
O
Внешние силы давления жидкости во входном и
выходном сечении направлены вдоль радиусов и
момента относительно оси Оz не создают
Для симметричной турбины сила тяжести проходит
через ось Oz и также
не создает.
момента
e
M O ( Fk ) M oz
Следовательно
Из (19) получаем:
M oz Gcek ( R1V1 cos 1 R2V2 cos 2 )
- турбинное уравнение Эйлера
33. 32. Решение задач
Напомним рекомендации к решению задач:1
2
3
4
5
Выбрать механическую систему (удачно!)
Изобразить все нужные силы (активные и
реакции связей)
Записать одну из общих теорем
динамики(или несколько)
Проинтегрировать полученную систему
уравнений. Постоянные интегрирования
определяются при этом из дополнительных
(начальных) условий задачи
Определить искомые величины
34. 33. Задача 1
zRB
u
r
R
P
Q
RA
A
Дано: платформа однородная веса P,
радиуса R, трения в опорах нет, ось z –
вертикальная, при t=0 человек веса Q
покоился. (0) 0
Определить , если человек пойдет
по платформе на расстоянии r с
относительной скоростью u.
Решение. 1. М.С. – платформа + человек
2. Внешние силы: P,Q,RA,RB
3.
dK
z
dt
4,5.
M z ( Fke ) 0 K z const
J z 0 (Q / g )r 2 0 J z (Q / g )r ( r u ); J z PR 2 / 2 g
( PR 2 2Qr 2 ) 0 2Qru
PR 2 2Qr 2
Проанализировать ответ!
35. 34. Задача 2
Дано: две одинаковые обезьяны сидятна концах каната. Первая – ползет все
R
время по канату вверх, вторая –
O
v
v
просто сидит. Какая из обезьян
u
окажется наверху быстрее?
Считать канат и блок невесомыми,
m1g
m2g
трением в блоке пренебречь.
Решение. 1. М.С. – обе обезьяны + канат + блок
2. Внешние силы: m1g, m2g, R0
e
3. dK o
0
k
k
dt
4,5.
M o ( Fk ) m1 gr m2 gr 0 K 0 const 0
K o rm1V1 rm2V2 0; V1 u Vk ; V2 Vk
m1 m2 Vk u / 2; V1 V2 u / 2
Обезьяны поднимутся одновременно!
Если бы вторая обезьяна тоже ползла, то
они поднялись бы вдвое быстрее! Vk 0; V1 V2 u
36. 35. Задача 3
yN
O
C
Fтр
P
α
Дано: однородный цилиндр массы
m, катится без проскальзывания
по плоскости с углом наклона
Трением качения пренебречь. Найти
ускорение цилиндра aC
x
mg
Решение. 1. М.С. – цилиндр
2. Внешние силы: mg, Fтр, N
3. ДУ плоского движения: m x C
F mg sin F
J M ( F ) F R
e
kx
тр
e
m y C Fkye N mg cos ;
C
C
k
тр
4,5. y C 0 N mg cos ;
P МЦС VC / R; aC / R x C / R
2
Имеем: maC mg sin Fтр ; N mg cos ; J C aC Fтр R
J C mR2 / 2 Fтр maC / 2 aC 2 g sin / 3
Замечание Fтр fN tg f
Иначе будет
проскальзывание!
37. 36. Заключение
1. Изучена теорема моментови ее частные случаи - законы сохранения
момента импульса
2. Выведены ДУ поступательного,
вращательного и плоского движения
твердого тела
3. Приведены примеры применения
теоремы моментов к движению Земли
вокруг Солнца, к движению жидкостей, к
физическому маятнику
4. Рассмотрены решения задач с
использованием теоремы моментов
38. 37. Вопросы для самоконтроля
1. Как определяется и для чего вводится момент количествадвижения системы?
2. Чему равен момент количества движения твердого тела
относительно оси его вращения?
3. Как связаны моменты количеств движения относительно
разных точек?
4. В чем состоит теорема моментов для системы?
5. Справедлива ли она с системе отсчета, движущейся
поступательно с центром масс системы?
6. Когда сохраняется момент количества движения системы
относительно точки? А относительно оси?
7. Зачем фигурист прижимает руки к туловищу, если он хочет
вращаться быстрее?
8. Можно ли изменить момент количества движения за счет
внутренних сил? А момент инерции относительно оси?
9. В чем аналогия между поступательным и вращательным
движением твердого тела?
39. 38. Вопросы для самоконтроля
10. Как происходит движение материальной точки поддействием центральной силы?
11. Что называют физическим маятником? Каким
уравнением описываются его малые колебания?
12. Какой вид имеют ДУ вращательного, поступательного и
плоского движения твердого тела?
13. Можно ли составить ДУ произвольного движения
твердого тела?
14. Каковы основные этапы решения задач на применение
теоремы моментов? В каких случаях удобно использовать
именно эту теорему?
40. Тема следующей лекции
Теорема об изменениикинетической энергии
системы





































 physics
physics








