Similar presentations:
3сем_Лк 14_6_Ряд Фурье
1.
Первое высшее техническое учебное заведение РоссииСанкт-Петербургский горный университет императрицы Екатерины II
Лекция 5
Ряд Фурье
14.12.2025
г. Санкт-Петербург
2025
1/11
2.
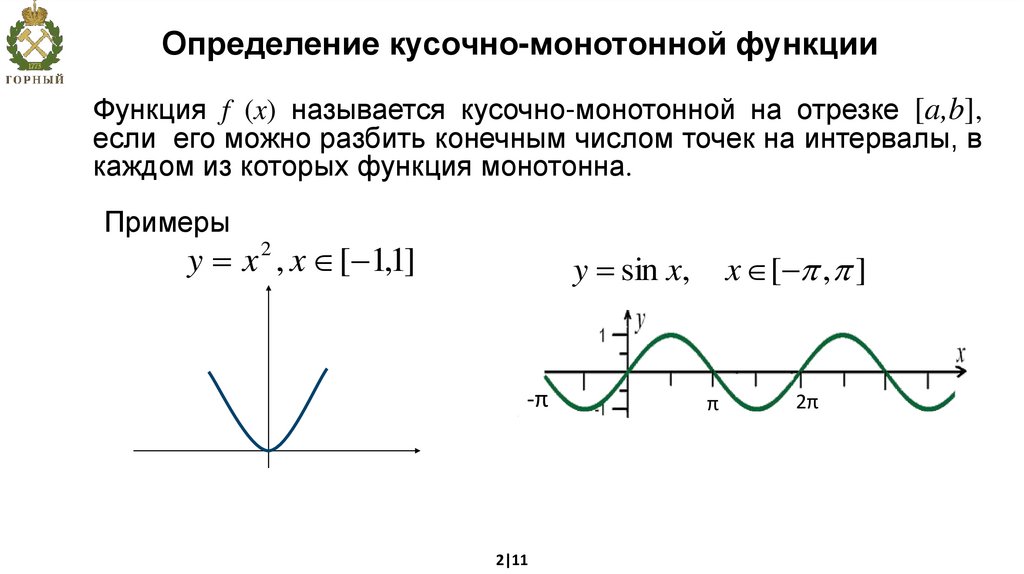
Определение кусочно-монотонной функцииФункция f (x) называется кусочно-монотонной на отрезке [a,b],
если его можно разбить конечным числом точек на интервалы, в
каждом из которых функция монотонна.
Примеры
y x , x [ 1,1]
2
x [ , ]
y sin x,
-π
2|11
π
2π
3.
Теорема ДирихлеЕсли периодическая с периодом 2 функция
– кусочно-монотонна,
– непрерывна на отрезке [- , ] или имеет на нем конечное число точек
разрыва 1-го рода,
то ряд Фурье этой функции сходится во всех точках отрезка [- , ],
причем сумма полученного ряда равна значению функции f(x) в точках
непрерывности функции
S ( x) f ( x),
а в точках ее разрыва сумма ряда равна среднему арифметическому левого
и правого пределов функции
f x0 0 f x0 0
S ( x0 )
2
3|11
4.
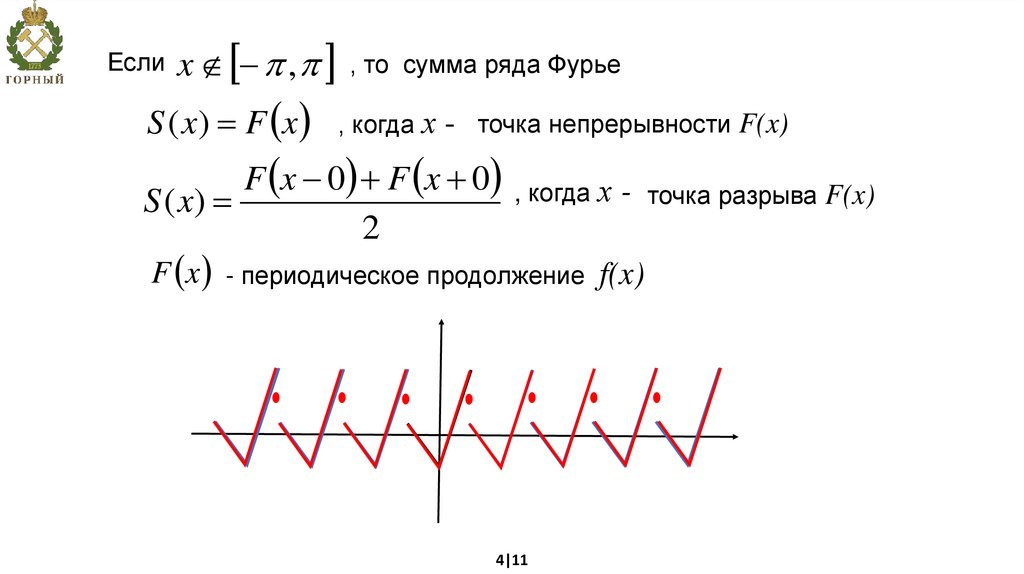
Если x ,S ( x) F x
, то сумма ряда Фурье
, когда х - точка непрерывности F(x)
F x 0 F x 0 , когда х - точка разрыва F(x)
S ( x)
2
F x - периодическое продолжение f(x)
4|11
5.
a0f ( x) an cos nx bn sin nx
2 n 1
1
1
1
a0 f ( x)dx, an
f ( x) cos nxdx, bn f ( x) sin nxdx
Пример. f ( x ) x, ( , )
2
1
x
1
a0
( x)dx x
2
5|11
2 2
1
2
6.
u xdu dx
an
( x) cos nxdx
1
dv cos nxdx v sin nx
n
dv
u
1
1
1
( x) sin nx
n
1
1
sin nxdx
cos
nx
2
n
n
1
=0
2 (cos n cos n( )) 0
n
u x
du dx
bn
( x) sin nxdx
1
dv sin nxdx v
cos nx
n
dv
u
1
2
1
1
1
1
2
1
n
( x)
cos nx
cos nxdx
cos
n
(sin
nx
)
( 1)
2
n
n
n
n
n
=0
6|11
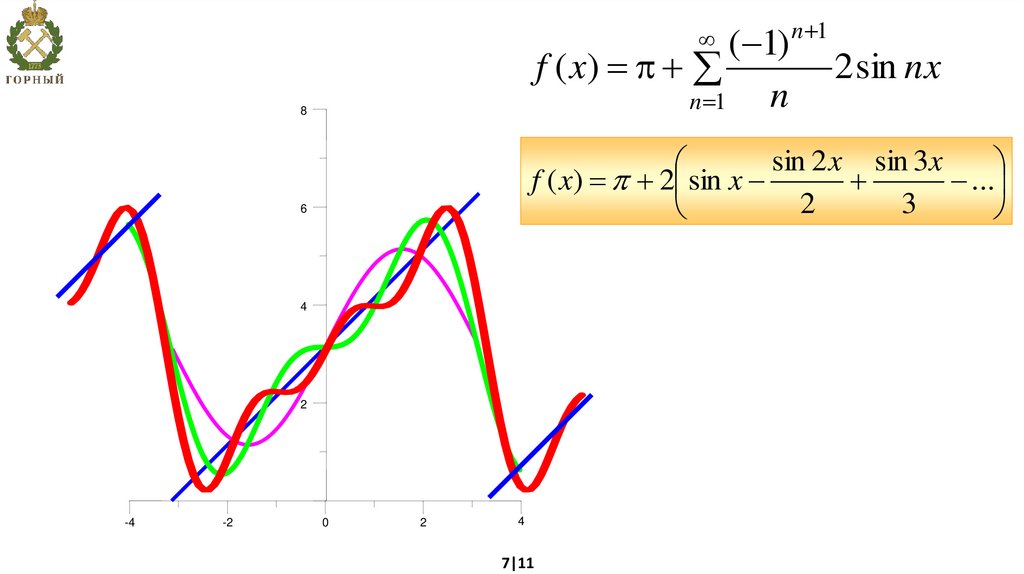
7.
( 1) n 1f ( x)
n 1
8
sin 2 x sin 3x
f ( x) 2 sin x
...
2
3
6
4
2
-4
-2
n
2 sin nx
0
2
4
7|11
8.
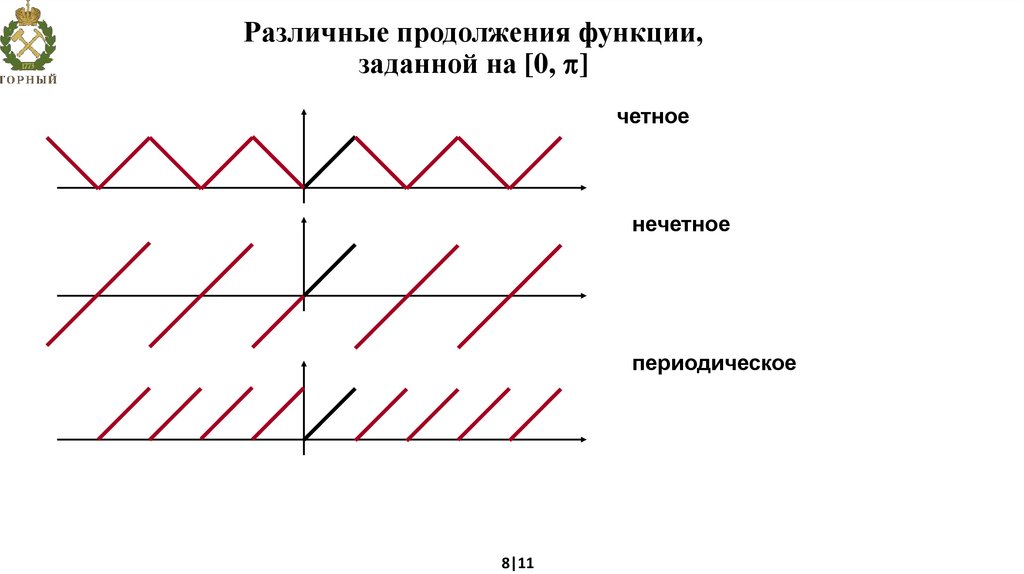
Различные продолжения функции,заданной на [0, ]
четное
нечетное
периодическое
8|11
9.
Ряд Фурьедля четной и нечетной функций
для четной
2
a0 f ( x)dx,
0
a0
f ( x) ak cos kx bk sin kx для нечетной
2 k 1
a0 0,
ak 0
2
ak f ( x) cos kxdx,
0
bk
1
bk
f ( x) sin kx dx 0
2
0
f ( x) sin kxdx
f ( x)
a0
f ( x)
a k cos kx
2
k 1
b sin kx
k
k 1
b1 sin x b2 sin 2 x b3 sin 3x +…
a0
a1 cos x a 2 cos 2 x a3 cos 3x +…
2
9|11
10.
Пример. Разложить в ряд Фурье по косинусамa0
2
2
f
x
dx
2
2 x
x dx
2
0
f ( x) x, (0, )
=0
0
0
2
2
sin
kx
1
2
x
cos
kx
dx
sin kxdx
x
ak
f x cos kx dx
k 0 k 0
0
u
0
dv
k 2n, n 1,2,3...
0,
1
2
k
2 cos kx
1
1
4
2
k
2 , k 2n 1, n 1,2,3...
k
0
2
k
bk 0, k 1,2,3...
1
4
1
1
f x
cos
2
n
1
x
cos x 2 cos 3x 2 cos 5x ... ,
2
2 n 1 2n 1
2
3
5
4
10|11
11.
Разложение периодической функции в ряд ФурьеДля периодической функции
с периодом
f(x)
2
f ( x)dx f ( x)dx,
2π выполняется
для любого
числа .
При вычислении коэффициентов Фурье можем промежуток интегрирования (– , )
заменить промежутком ( , +2 ), т.е.
a0
1
2
f ( x)dx,
an
1
2
f ( x) cos nxdx,
bn
a0
S ( x)
a k cos kx bk sin kx
2
k 1
11|11
1
2
f ( x) sin nxdx
12.
Ряд Фурье для 2l–периодической функции на [-l, l ]
Сумма ряда
l
1
a0 f ( x)dx,
l l
t
x [-l, l ]
a0
k
k
S ( x)
a k cos
x bk sin
x,
2
l
l
k 1
1
ak
l
l
l
kx
гармоник
и
1
f ( x) cos
dx, bk
l
l
x
l t [- , ]
где
l
f ( x) sin
kx
l
l
f ( x) s n ( x)
Приближение периодической функции рядом Фурье:
a0
s n ( x)
a1 cos x b1 sin x a 2 cos 2 x b2 sin 2 x ... a n cos nx bn sin nx
2
наименьшее среднеквадратичное отклонение от функции f(x) у того тригонометрического
многочлена, коэффициенты которого являются коэффициентами Фурье этой функции f(x)
12|11
dx,
13.
Спасибо за вниманиеСанкт-Петербургский горный
университет
императрицы Екатерины II,
199106, г. Санкт-Петербург,
Малый пр. В.О., д. 83
Тел.: +7(812) 328-82-98;
11|11


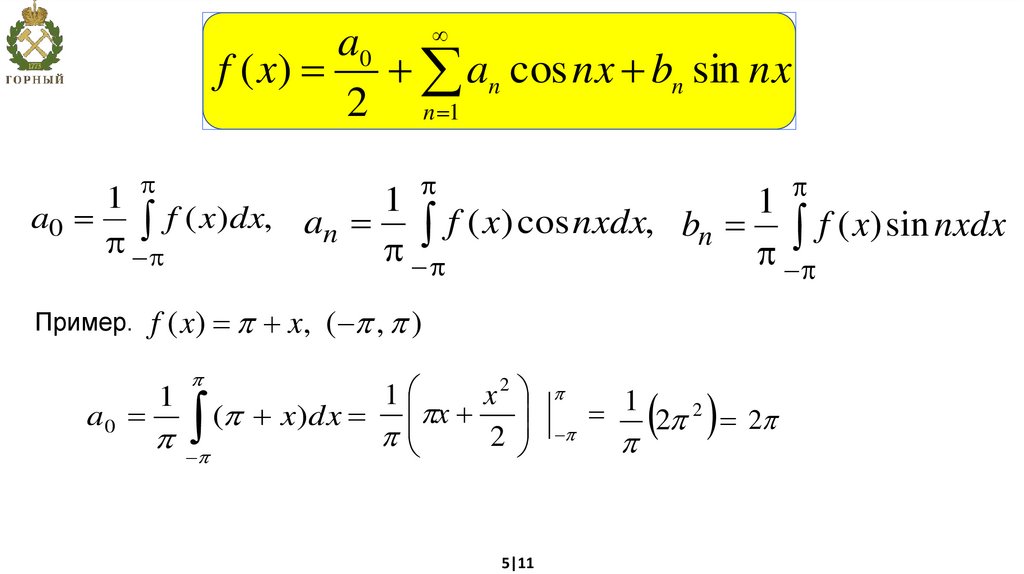
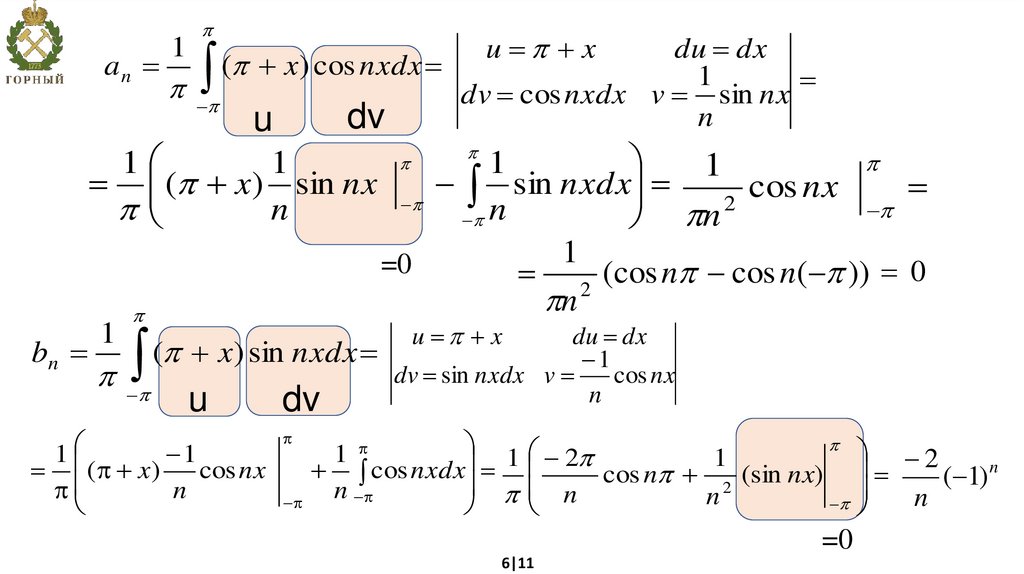





 mathematics
mathematics








