Similar presentations:
75646 (1)
1. Лекція 6 Векторна алгебра ПЛАН
1.Векторний добуток векторів.2.Властивості векторного добутку.
3.Мішаний добуток векторів та його
властивості.
2.
1. Векторний добуток векторівВекторним добутком вектора a на вектор b
називається вектор с , в якого:
1) довжина чисельно дорівнює площі
паралелограма, побудованго на цих векторах;
2) вектор с перпендикулярний
до
площини,
в
якій
лежать вектори
a і b , тобто
c a і c b ;
3) вектор с напрямлений таким чином, щоб
найкоротший поворот від вектора a до b
здійснювався проти годинникової стрілки, якщо
дивитись на нього з кінця вектора c .
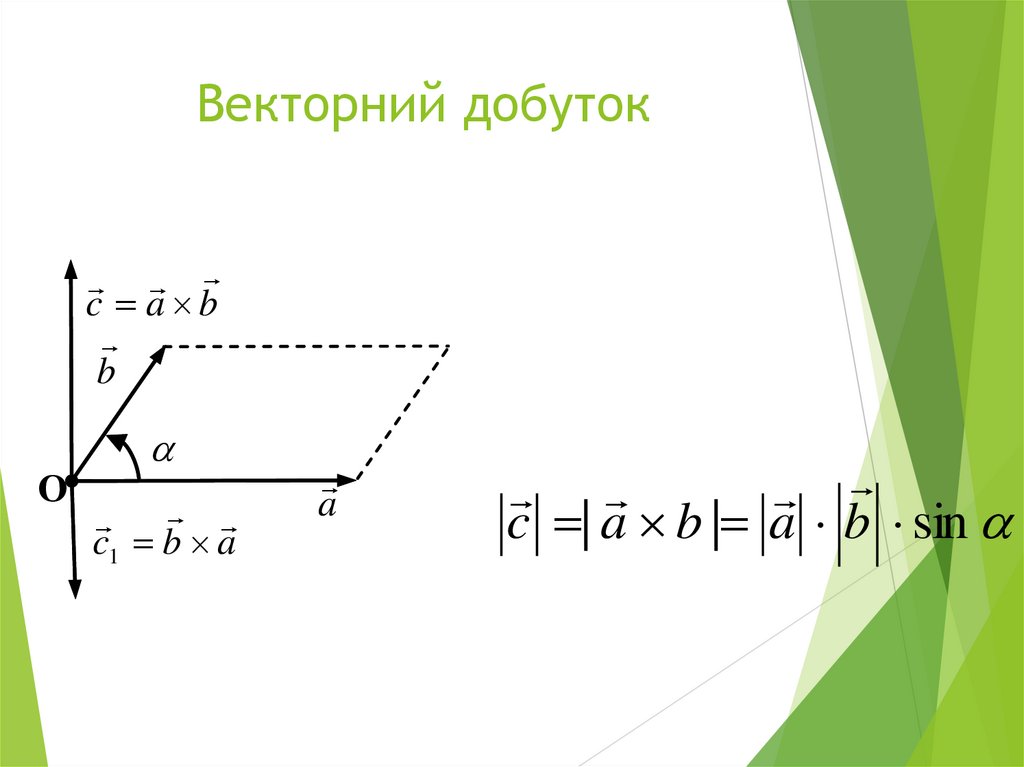
3. Векторний добуток
c a bb
О
c1 b a
a
c | a b | a b sin
4. Властивості векторного добутку
1.Властивості векторного добутку[a , b ] [b , a ] - антикомутативність;
[ a, b ] [a, b ]; [a, b ] [a, b ]
асоціативність відносно скалярного
множника;
[a b , c ] [a , c ] [b , c ]
дистрибутивність
відносно додавання;
[a , b ] 0
означає колінеарність векторів a і b .
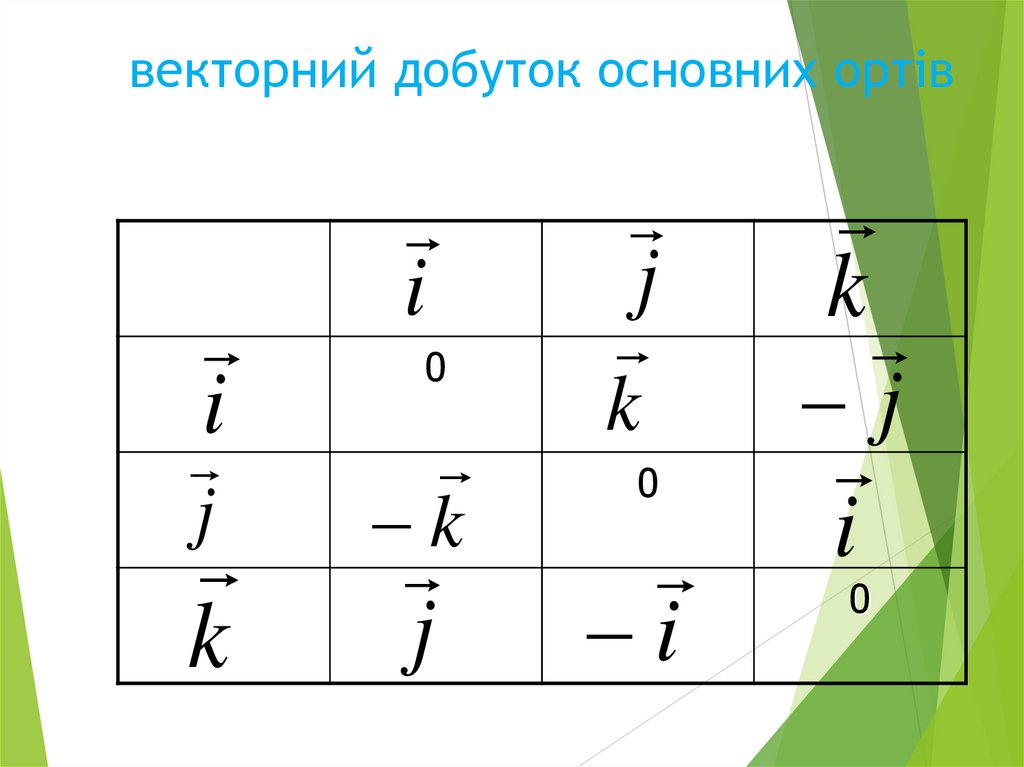
5. векторний добуток основних ортів
ij
k
i
0
k
j
j
k
0
i
k
j
i
0
6. Вираз векторного добутку через координати
Якщо a {a x , a y , a z } b x , y , z ,,2
2
2
тоді
i
a b x1
x2
j
k
y1
y2
z1
z2
7. Геометричний зміст
Площа паралелограмаПлоща трикутника
S а b
1
S a b
2
8. 3. Мішаний добуток векторів та його властивості
Мішаним добутком трьох векторівa, b
і
c
називається
число, яке отримуємо, якщо перемножимо вектори
b векторно,
а
потім
скалярно на вектор c .
отриманий
вектор
a
і
помножимо
a , b , c ([ a , b ], c )
9. Геометричний зміст
Мішаний добутокнекомпланарних
векторів a , b і c по модулю дорівнює
об’єму паралелепіпеда,
побудованого на
векторах a, b , c .
Вектори a , b і c задані своїми координатами в
прямокутній системі координат
a x1 , y1 , z1 ; b x 2 , y 2 , z 2 , c x 3 , y 3 , z 3
10.
x1a, b , c x2
x3
y1
y2
y3
z1
z2
z3
11.
Умова компланарностіx1
x2
x3
y1
y2
y3
z1
z2 0
z3
12. Властивості мішаного добутку
([ a , b ], c ) ( a , [b , c ])a, b , c b , c , a c , a, b
a, b , c b , a, c
13. Подвійний векторний добуток
Подвійним векторним добуткомвекторів a , b , c називається вираз виду
[ a,[b, c ]] .
[a,[b, c]] b(a, c) c(a, b)
14. Рекомендована література
1. Резніков С.І., Зінькевич О.П., Сафонов В.М. та ін. Вища та прикладнаматематика: навч. посіб. для студ. вищ. навч. зак. К.: НУХТ, 2016. 343 с.
2. Тінгаєв О.А., Іванченко Є.А, Мельничук В.С. Вища та прикладна математика:
навч. посіб. Одеса, 2018. Ч. 1. 240 с
3. Литвинов А.Л. Вища та прикладна математика з елементами інформаційних
технологій: навчальний посібник. Харків: ХНУМГ ім. О.М. Бекетова, 2019. 232
с.
4. Фортуна В.В., Бескровний O.I. Вища та прикладна математика: навч. посіб.
для студ. ден. форми навчання екон. спец. Львів: «Магнолія 2006», 2017. 647
с
5. Дубчак В.М., Новицька Л.І., Дячинська О.М. Вища математика. Приклади та
задачі: Навчальний посібник. Вінниця: ТОВ «ТВОРИ». 2021. 365 с.







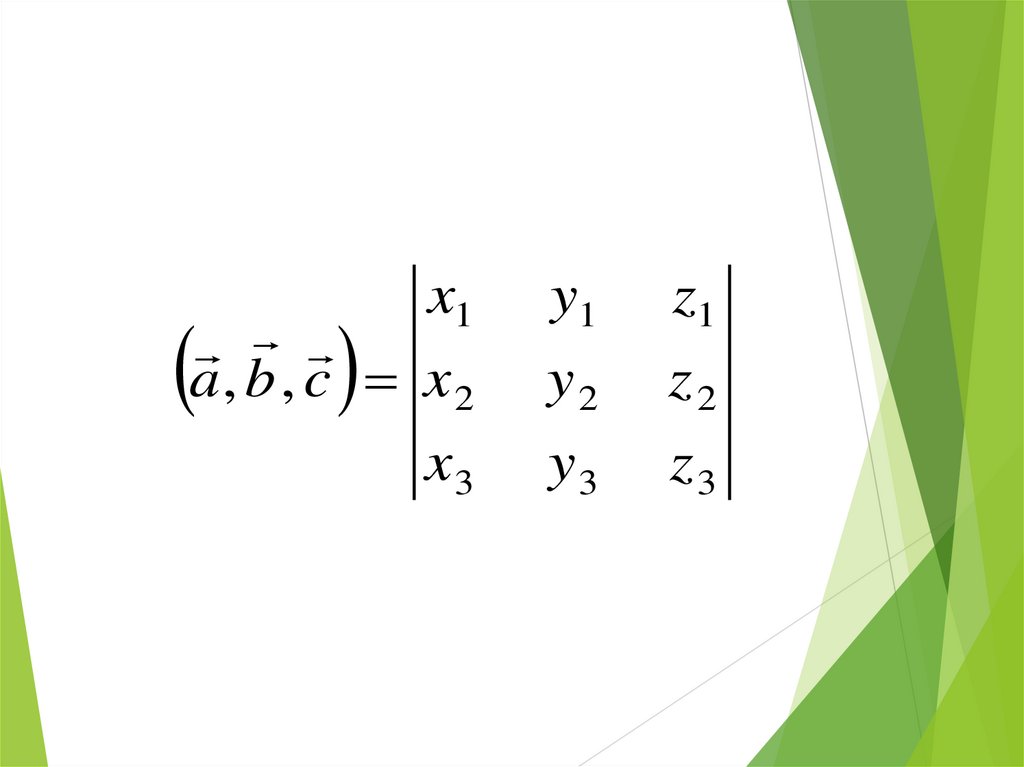




 mathematics
mathematics








