3сем_Лк 12_4_Ряд Тейлора

1.

Первое высшее техническое учебное заведение России
Санкт-Петербургский горный университет императрицы Екатерины II
Лекция 4
РАЗЛОЖЕНИЕ ФУНКЦИЙ В
СТЕПЕННЫЕ РЯДЫ
10.12.2025
г. Санкт-Петербург
2025
1/11

2.

Пусть f(x) бесконечно дифференцируема
в точке a и ее окрестности
Представить f(x) как сумму
ряда:
f ( x)
n 0
cn ( x a) n c c ( x a) c ( x a) 2 +… c ( x a) n +… (1)
1
n
2
0
f (a) c 0
n 1
f (x) c1 2c 2 ( x a ) +… ncn ( x a) +…
f (a ) c1
f (x ) 2c 2 3 2c3 ( x a) +… n(n 1)c n ( x a) n 2 +…
f (a ) 2c 2
Продифференцируем ряд (1) n раз:
f ( x) c n n! (n 1)n 2c n 1 ( x a) +…
n
f
(n)
(a) n!c n
2|11
cn f
(n)
(a)
n!

3.

Теорема. Если функция f(x) разложима в степенной ряд (1),
сходящийся при
x а R,
то коэффициенты ряда вычисляются по формуле:
Ряд Тейлора:
f ( x)
n 0
f
(a)
n
( x a)
n!
n 0
ряд Маклорена:
f ( x)
f
(n)
n 0
f
(n)
(a)
n
( x a) сходился в интервале
n!
x а R и его сумма s=f(x) необходимо и достаточно,
чтобы остаточный член формулы Тейлора
Rn ( x) 0
(a)
n!
При а=0
(n)
Теорема. Для того чтобы ряд
f
cn
(n)
n
3|11
f(x)=Pn(x)+Rn(x)
(0) n
x
n!

4.

Формула Тейлора
n
Pn(x)=
k 0
f
f(x) = Pn(x) + Rn(x)
f (a)
(a)
f (a)
n
k
( x a) f (a)
( x a)
( x a) +…
k!
n!
1!
(n)
(k )
многочлен Тейлора
Необходимость
f ( n ) (a)
( x a) n сх–ся и его сумма f(x) lim Рn ( x) f ( x) R n ( x ) 0
n!
n
n 0
Достаточность
Rn ( x) 0
n
из формулы f(x) = Pn(x) + Rn(x) lim Рn ( x) f ( x)
степенной ряд сх–ся
f ( x)
n 0
4|11
n
f
(n)
(a)
n
( x a)
n!

5.

Разложения элементарных функций в ряд Маклорена:
f ( x)
n 0
f
(n)
(0) n
x
n!
f(n)(х)= ex f(n)(х)= 1
f(х)= ex
2
3
n
x x
x
x
e 1
...
...
1! 2! 3!
n!
x
Ряд сходится х
Признак Даламбера для ряда:
n 1
1 n
x
n!
n 0
an 1
x (n)!
1
lim
lim
x lim
0
1
n
n n 1
n ( n 1)! x
n a
n
n
x
Лемма. Справедлива формула: lim
0
n n!
5|11
ряд сходится x

6.

остаток ряда Маклорена
x
n 1
Rn (x) ( n 1)!
0
x n 1
R n (x )
e х 0<θ<1
( n 1)!
<1 при х<0
e x
x фиксировано
< ex при х>0
ограничена
f x sin x
f x cos x sin x
2
f x sin x sin x 2
2
f x cos x sin x 3
2
Rn ( x) 0
n
1 n
e
x
x (– ; )
n
!
n 0
x
f 0 0
n
f x sin x n
2
6|11
f 0 1
f 0 0
f 0 1

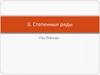
7.

3
5
x
x
( 1)
2 n 1
sin x x
–… (2n 1)! x
3! 5!
n 0
sin( x n
Оценим остаток:
Rn (x)
( n 1)!
2
n
)
x
n 1
1
x
n 1
(n 1)!
Rn ( x) 0
0
дифференцируем
f x cos x
степенной ряд sinx
Ряд сходится х
n
2n
n 2n
1
(
2
n
1
)
x
1 x
1
x
sin x
n 0
2n 1 !
2n !
2
n
1
!
n
0
n 0
n
2 n 1
1 x
x
x
cos x 1
–… 2n !
n 0
2! 4!
2
4
7|11
n
2n
Ряд сходится х
n

8.

f x ln 1 x
x <1 сходится
1 x x x +… ( x)
2
Интегрируем
x
степенной ряд на
отрезке [0, x] (–1,1)
0
x
3
dt
n n
( 1) t dt
( 1)
1 t 0 n 0
2
n 0
3
4
x
x
x
+…
x
2
3
4
ln 1 x
1
n 1
n 1 x
0
t dt
1
1 х
x n 1
n 1
Если х =1
n 1
1
n 1
n
Сходится по пр. Лейбница
n
n
n 0
x
n
n
n
сходится х (–1,1]
Если х = –1
1
n
n 1
Расходится как гармонич. ряд
8|11

9.

f x 1 x
m
f ( n ) (0) n
f ( x)
x
n!
n 0
m R
f 0 1
f x m 1 x
m 1
f 0 m
f x m m 1 1 x
m 2
1 x
m
f 0 m m 1
m m 1 2 m m 1 m 2 3
m
m m 1 ... m n 1 n
x
x
1 x
x +…
n!
2!
3!
1!
n 0
Исследуем его на
сходится х (–1,1)
сходимость по
признаку Даламбера
Биномиальный ряд
при х = 1 сходимость ряда зависит от m
9|11

10.

Пример 1. Разложить в ряд по степеням x (ряд Маклорена) функцию
1 1
1 2 x
1 cos 2 x 1 1
cos 2 x
sin x
2n !
2 2 n 0
2 2
2
n 2n
1 t
cos t
t
2
x
2n !
n 0
2
n
2n
f ( x) sin x
2
( 1) 4 2 n
1 1
x
2 2 n 0 ( 2n) !
n
a
Пример 2. Вычислить интеграл
e
x2
dx
0
n
t
t
e
n!
n 0
t x
2
2
4
x
x
n x
x
1
e 1
2!
1
!
n
!
n 0
2
2n
10|11
6
x
+…
3!
n

11.

Спасибо за внимание
Санкт-Петербургский горный
университет
императрицы Екатерины II,
199106, г. Санкт-Петербург,
Малый пр. В.О., д. 83
Тел.: +7(812) 328-82-98;
11|11