Основные теоремы дифференциального исчисления. Правило Лопиталя. Формулы Тейлора и Маклорена

1.

Первое высшее техническое учебное заведение России
Санкт-Петербургский горный университет императрицы
Екатерины II
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
ЛЕКЦИЯ 4
Основные теоремы дифференциального
исчисления. Правило Лопиталя.
Формулы Тейлора и Маклорена.
05.03.2025
1|22

2.

Содержание лекции
• Теоремы Ферма, Ролля, Лагранжа, Коши;
• Правило Лопиталя;
• Формулы Тейлора и Маклорена
с остаточным членом в форме Лагранжа.
2|22

3.

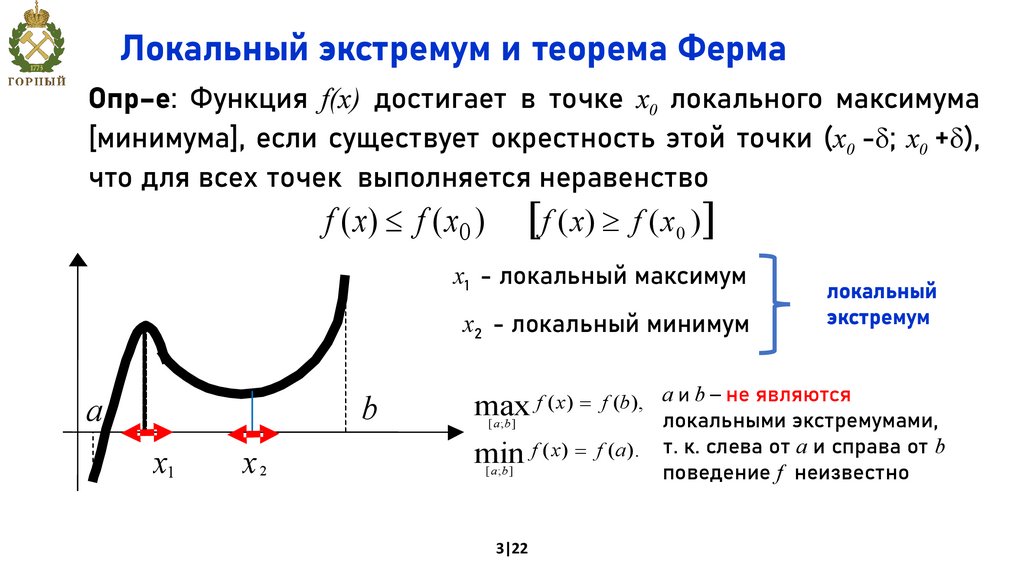
Локальный экстремум и теорема Ферма
Опр–е: Функция f(х) достигает в точке х0 локального максимума
[минимума], если существует окрестность этой точки (х0 - ; х0 + ),
что для всех точек выполняется неравенство
[f ( x ) ³ f ( x 0 ) ]
f ( x) £ f ( x0 )
х1 - локальный максимум
х2 - локальный минимум
b
a
x1
x2
локальный
экстремум
и b – не являются
max f ( x) = f (b), aлокальными
экстремумами,
[ a ;b ]
min f ( x) = f (a).
[ a ;b ]
3|22
т. к. слева от а и справа от b
поведение f неизвестно

4.

Теорема Ферма:
Если функция y=f(x) имеет производную в точке х0 и достигает
в этой точке локального экстремума, то f ¢( x0 ) = 0
Доказательство:
Пусть функция f в точке х0
f ( x) £ f ( x0 )
имеет локальный максимум
По определению производной:
f ( x0 + Dx) - f ( x0 )
f ¢( x0 ) = lim
Dx
Dx ® 0
переходя к
lim
Dx ® 0
x = x0 + Dx
f ¢( x0 ) £ 0
Þ
f ¢( x0 ) ³ 0
4|22
Dx > 0 f ( x) - f ( x0 ) £ 0
³0
Dx
Dx < 0
f ¢( x ) = 0
0

5.

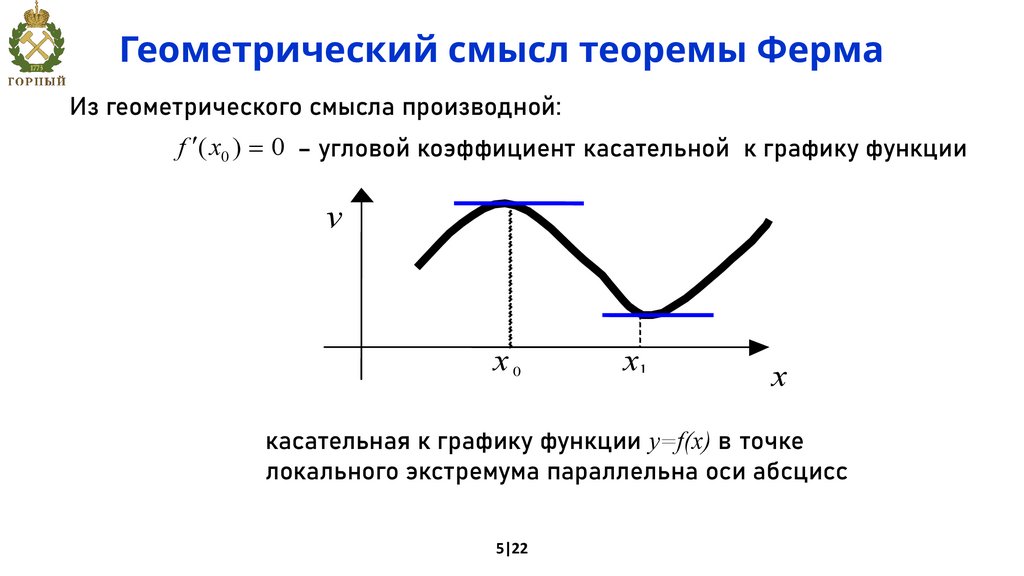
Геометрический смысл теоремы Ферма
Из геометрического смысла производной:
f ¢( x0 ) = 0 – угловой коэффициент касательной к графику функции
y
x0
x1
x
касательная к графику функции y=f(x) в точке
локального экстремума параллельна оси абсцисс
5|22

6.

Теорема Ролля:
Если функция f (x) : 1) непрерывна на отрезке [a, b] ,
2) дифференцируема в интервале (a, b) , 3) f (a) = f (b) ,
то существует точка c Î (a; b) , в которой f ¢(c) = 0 .
Доказательство:
(теорема Вейерштрасса)
f(x) принимает наибольшее М m £ f ( x) £ M
и наименьшее m значения
функция f (x) непрерывна
на отрезке [a, b]
Возможны два случая:
1) Если m=M, то f(x)=const
f ¢( x) = 0 качестве точки с
можно взять любую из (a;b)
2) Если m M, то m<M
Т.к. f (a) = f (b) , то хотя бы одно из значений М или m
достигается в некоторой точке c Î (a, b) .
6|22
по теореме Ферма
f ¢(c) = 0

7.

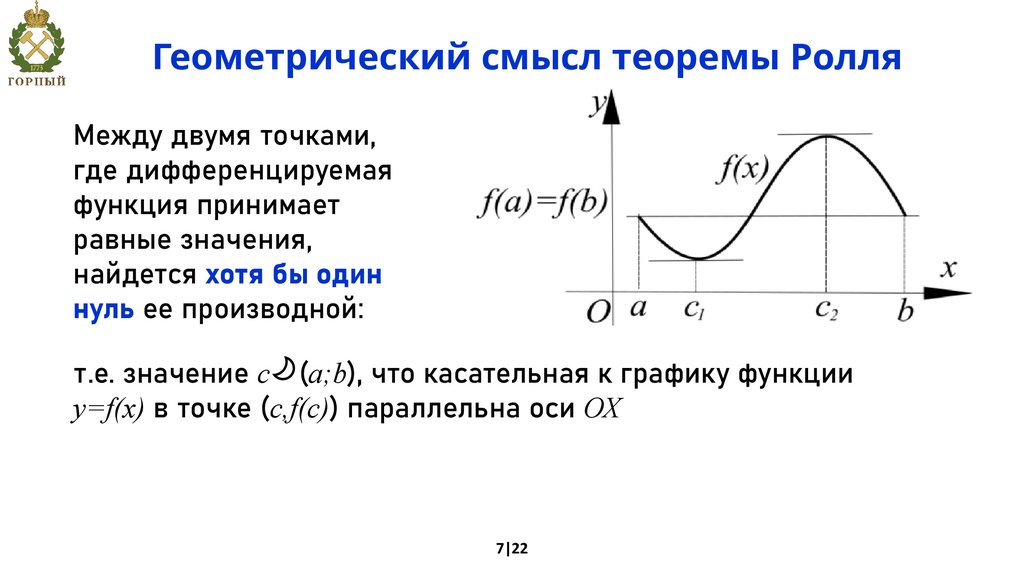
Геометрический смысл теоремы Ролля
Между двумя точками,
где дифференцируемая
функция принимает
равные значения,
найдется хотя бы один
нуль ее производной:
т.е. значение с (a;b), что касательная к графику функции
y=f(x) в точке (c,f(c)) параллельна оси ОХ
7|22

8.

Замечание. Если хотя бы одно требование теоремы Ролля нарушается,
то утверждение теоремы может оказаться неверным.
Пример 1. Функция f ( x) = x на отрезке [-1; 1]
f(х) непрерывна и f(-1)=f(1)
Нарушается условие дифференцируемости
не существует производная в точке х=0
Внутри отрезка не существует точки, в
которой производная обращается в 0
8|22

9.

Теорема Коши
Если функции f(x) и g(x) непрерывны на [a;b] и дифференцируемы на (a;b),
причем g ¢( x) ¹ 0 (a;b), то существует точка c (a;b) такая, что
Доказательство:
f (b) - f (a )
f ¢(c)
=
g (b) - g (a ) g ¢(c)
Отметим, что g(b)-g(a) 0, т. к. в противном случае, по теореме Ролля
нашлась бы точка с и g ¢(c) = 0 (этого не может быть по условию теоремы)
Рассмотрим вспомогательную функцию :
F(x) – линейная комбинация функций
непрерывна на [a;b],
дифференцируема на (a;b)
9|22
F ( x ) = f ( x ) - lg ( x ) , l Î R
Найдем : F(a)=F(b)=0

10.

F ( x ) = f ( x ) - lg ( x )
f
(
b
)
f
(
a
)
f (а ) - lg (a ) = f (b) - lg (b) l =
.
g (b) - g (a )
F(x) – удовлетворяет всем условиям теоремы Ролля.
$c Î ( a; b ) : F ¢( c ) = 0
F ¢( x) = f ¢( x) - lg ¢( x)
¢
f
(
c
)
=l
g ¢(c)
F ¢(c) = f ¢(c) - lg ¢(c) = 0
f (b) - f (a )
f ¢(c)
=
g (b) - g (a ) g ¢(c)
10|22

11.

Теорема Лагранжа (о среднем)
Если функция f (x) : 1) непрерывна на отрезке [a, b] , 2)дифференцируема
в интервале (a, b) , то найдется по крайней мере одна точка c Î (a, b) , что
f (b) - f ( a ) = f ¢(c)(b - a ).
Доказательство следует из теоремы Коши при g(x)=x получим:
f (b) - f (a ) f ¢(c)
=
= f ¢(c)
b-a
1
f ( x + Dx) - f ( x) = f ¢( x + tDx)Dx,
Если считать a = x, b = x + Dx , то получим:
c = x + tDx, 0 < t < 1.
Dу = f ¢( x + tDx)Dx
Формула конечных приращений Лагранжа дает точное выражение для
приращения функции в отличие от приближенного равенства:
у f ¢( x0 ) x
11|22

12.

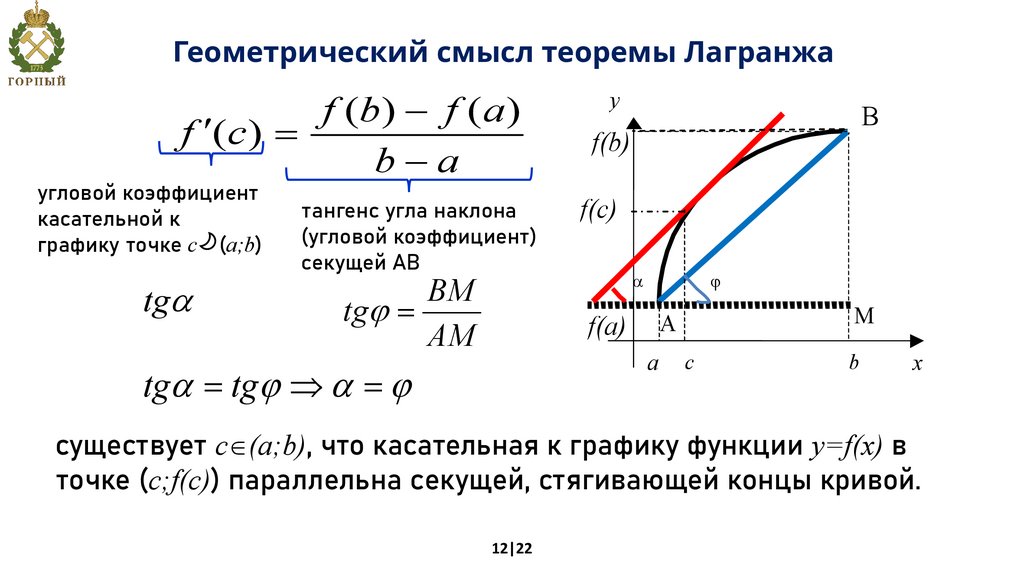
Геометрический смысл теоремы Лагранжа
f (b) - f ( a )
f ¢(c ) =
b-a
угловой коэффициент
касательной к
графику точке с (a;b)
tga
тангенс угла наклона
(угловой коэффициент)
секущей АВ
ВМ
tgj =
АМ
y
B
f(b)
f(с)
a
tga = tgj Þ a = j
М
A
f(a)
c
b
x
существует с (a;b), что касательная к графику функции y=f(x) в
точке (c;f(c)) параллельна секущей, стягивающей концы кривой.
12|22

13.

ì0 ü
Правило Лопиталя для неопределенности í ý
î0 þ
Пусть функции f (x) и g (x) удовлетворяют условиям:
1) f (x) и g (x) дифференцируемы в некоторой окрестности точки a
(исключая, может быть, саму точку a ) и g ¢( x) ¹ 0 в этой окрестности;
2) lim f ( x) = lim g ( x) = 0 ;
f ¢( x)
Если существует предел отношения производных lim
(конечный
x ®a g ¢( x )
f ( x)
или бесконечный), то существует предел lim
:
x® a g ( x )
x ®a
x ®a
f ( x)
f ¢( x)
lim
= lim
.
x ®a g ( x )
x ®a g ¢( x )
sin px ì 0 ü
p cos px p cos 2p
(
sin px )¢
Пример. Найти lim
=
= p.
= lim
í ý =lim
x ®2 x - 2 î 0 þ x ®2
1
(x - 2)¢ x®2 1
13|22

14.

ì¥ ü
Правило Лопиталя справедливо для неопределенности í ý
î¥ þ
f ¢( x)
0
Если выражение g ¢( x) - неопределенность 0 ,
Замечание 1.
Замечание 2:
функции f ¢(x) и g ¢(x) удовлетворяют условию теоремы, то
f( x)
f ¢( x )
f ¢¢( x )
lim g( x ) = lim g¢( x ) = lim g¢¢( x )
x® a
x® a
x® a
Замечание 3.
0
0
¥
0
×
¥
,
0
,
¥
¥
¥
,
1
Неопределенности
,
алгебраическими
0 ¥
преобразованиями сводят к неопределенностям 0 , ¥ , чтобы применить
правило Лопиталя.
14|22

15.

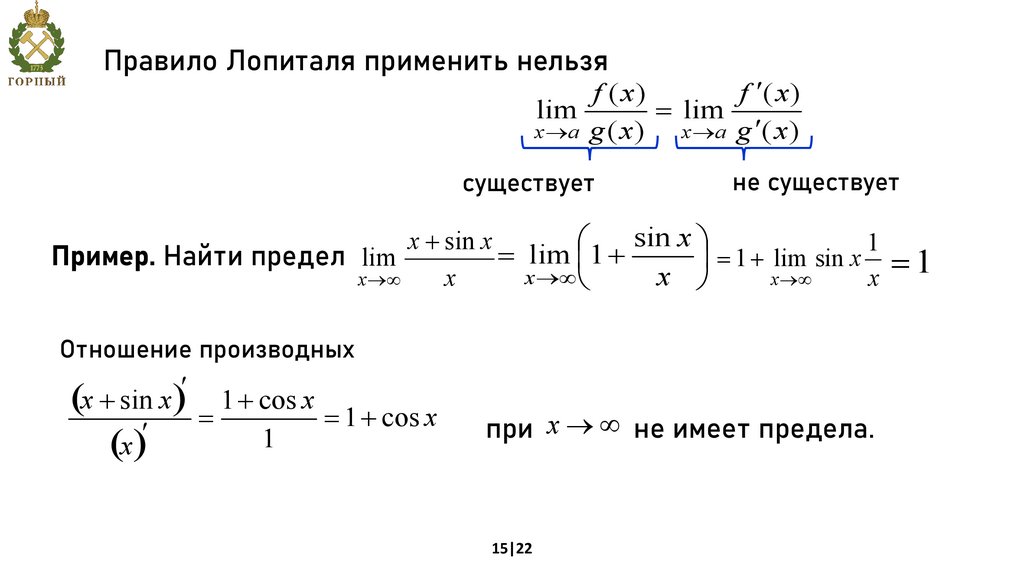
Правило Лопиталя применить нельзя
f ( x)
f ¢( x)
lim
= lim
x ®a g ( x )
x ®a g ¢( x )
существует
не существует
sin x ö
æ
x + sin x
1
=
lim
1
+
Пример. Найти предел lim
ç
÷ = 1 + lim sin x = 1
x ®¥ è
x ø
x ®¥
x ®¥
x
x
Отношение производных
(x + sin x
¢
(x )
¢
)
1 + cos x
=
= 1 + cos x
1
при x ® ¥ не имеет предела.
15|22

16.

{0 × ¥}
[
]
lim
f
(
x
)
g
(
x
)
=
,
то
lim
g
(
x
)
=
¥
если lim f ( x) = 0
x ®a
x ®a
x ®a
Пример. Найти lim (1 - x)tg
x®1
(
1 - x )¢
= lim
x®1
æ px ö
ç ctg ÷
2ø
è
¢
px
2
1 - x ì0 ü
=í ý=
= {0 × ¥} = lim
px î 0 þ
x®1
ctg
2
= lim
x ®1
-1
px ö
æ
- ç sin ÷
2 ø
è
-2
×
1
16|22
p
2
=
2
p
f ( x) ì 0 ü
lim
í ý
1
x®a
î0 þ
g ( x)
g ( x) ì ¥ ü
lim
í ý
1
x®a
î¥ þ
f ( x)

17.

{¥ - ¥} æ 1
0
0
¢
x
1
ln
x
0
(
ì ü
1 ö = {¥ - ¥}= lim
x - 1 - ln x )
=
Пример. limç
= lim
÷
=
í
ý
x
®
1
ln
x
(
x
1
)
x®1è ln x
x -1ø
¢
x®1
î0 þ
(ln x( x - 1) )
1
1- 0 x
¢
1
x -1
1
(
)
x
1
0
ì ü
lim
=
= í ý = lim
=
= lim
= lim
1
¢
x®1
x®1 1
x®1 (x ln x + x - 1)
x®1 x ln x + x - 1 î 0 þ
1 × ln x + x × + 1 2
( x - 1) + ln x × 1
x
x
¥
0
0
{1 }, {0 }, {¥ } :
Пример.
lim (cos x )
1
x2
x®0
lim
x ®0
ln(cos x)
x
2
ì 0 ü lim
=í ý=
î 0 þ x ®0
f
{1 }
¢
(ln(cos x))
(x )
2 ¢
g
¥
=e
g ln f
1
= lim e x
x ®0
2
, ( f > 0) {0 × ¥}
ln (cos x )
= e
lim
x ®0
- tg x ì 0 ü
1
х
1
= lim
= í ý = - lim = - .
x ®0 2 x
2 x ®0 х
2
î0 þ
17|22
ln (cos x )
x
2
=e
-
1
2 =
1
e
.

18.

Формула Тейлора
Пусть функция y = f (x) определена в некоторой окрестности точки
x = a и имеет все производные до (n + 1) -го порядка включительно.
Найти многочлен Pn (x) , чтобы он хорошо описывал функцию f (x)
в окрестности точки a :
Pn ( x ) = C 0 + C1 ( x - a ) + C 2 ( x - a ) 2 + C 3 ( x - a ) 3 + ... + C n ( x - a ) n .
и обладал свойствами:
Pn (a ) = f (a ) ;
Pn¢ (a ) = f ¢(a ); Pn¢¢(a ) = f ¢¢(a );...; Pn( n ) (a ) = f ( n ) (a )
(*)
Найдем производные от Pn (x) :
Pn¢ ( x ) = C1 + 2C 2 ( x - a ) + 3C 3 ( x - a ) 2 + ... + nC n ( x - a ) n -1 Pn¢ (а) = C1
2
Pn¢¢( x) = 2 × 1 × C 2 + 3 × 2 × C 3 ( x - a ) + ... + n( n - 1)C n ( x - a ) n -
Pn¢¢(а ) = 2!×C 2
(n)
Pn ( x ) = n( n - 1)(n - 2) × ... × 2 × 1 × C n
18|22
Pn( n) (а) = n!×C n

19.

Из условий (*):
f ¢(a ) = Pn¢ (a ) = C1 ;
f (a ) = Pn (a ) = C 0 ;
f ¢¢(a ) = Pn¢¢(a ) = 2!×C 2 ;
C 0 = f (a );
...
f
(n)
(n)
(a ) = Pn (a ) = n!×C n
1
1
(n)
...
¢
¢
C1 = f ¢(a ); C 2 = f (a);
C n = f (a ).
2!
n!
Искомый многочлен:
f ¢¢(a )
f ' (a)
2
Pn ( x) = f (a ) +
( x - a ) + ....
( x - a) +
2!
1!
(n)
f
(a)
n
+
(
x
a
)
.
Многочлен Тейлора
n!
19|22

20.

Формула Тейлора
f ( x) = Pn ( x) + Rn ( x)
Обозначим Rn ( x) = f ( x) - Pn ( x)
(n)
f '()()()
a
f ¢¢ a
f
a
2
f (x) = f (a) +
( x - a) +
( x - a ) + ... +
( x - a )n + Rn ( x ).
1!
2!
n!
Остаточный член в форме Лагранжа:
остаточный член
формулы Тейлора
f ( n +1) (c )
Rn ( x ) =
( x - a ) n +1 , где c Î (a, x).
( n + 1)!
При а=0
(n)
¢
¢
f ' (0)
f (0) 2
f ( 0) n
f ( x ) = f ( 0) +
x+
x + ... +
x + Rn ( x). Формула Маклорена
1!
2!
n!
( n +1)
f
(c ) n +1
Rn ( x ) =
x
, c Î (0, x)
( n + 1)!
20|22

21.

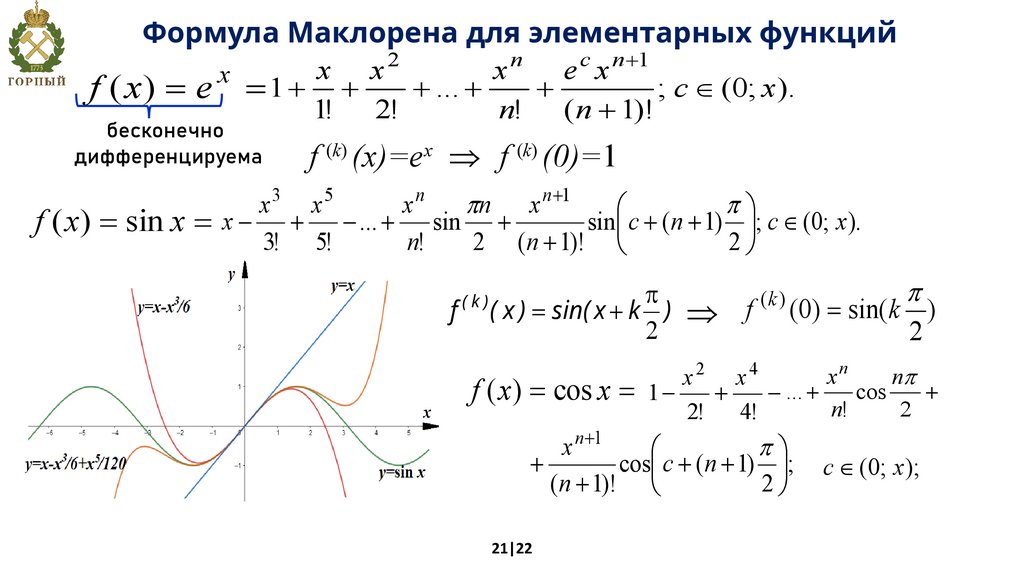
Формула Маклорена для элементарных функций
2
n
c n +1
x
x
x
e
x
x
+ ... +
+
; c Î (0; x).
f ( x) = e = 1 + +
1! 2!
n! ( n + 1)!
бесконечно
дифференцируема
f (k) (x)=ex f (k) (0)=1
x3 x5
xn
pn x n+1
pö
æ
sin ç c + (n + 1) ÷; c Î (0; x).
f ( x) = sin x = x - + - ... + sin +
3! 5!
n!
2 (n + 1)! è
2ø
f
(k)
p
( x ) = sin( x + k )
2
f
(k )
p
(0) = sin(k )
2
xn
np
x2 x4
f ( x) = cos x = 1 - + - ... + cos +
n!
2
2! 4!
x n+1
pö
æ
+
cosç c + (n + 1) ÷;
(n + 1)! è
2ø
21|22
c Î (0; x);

22.

Спасибо за внимание
Санкт-Петербургский горный
университет
императрицы Екатерины II,
199106, г. Санкт-Петербург,
Малый пр. В.О., д. 83
Тел.: +7(812) 328-82-98;
22|22