Similar presentations:
Дифференциальное исчисление функций одной действительной переменной 13. Теоремы о среднем. Формула Тейлора. Правило Лопиталя
1. Дифференциальное исчисление функций одной действительной переменной
13. Теоремы о среднем.Формула Тейлора.
Правило Лопиталя.
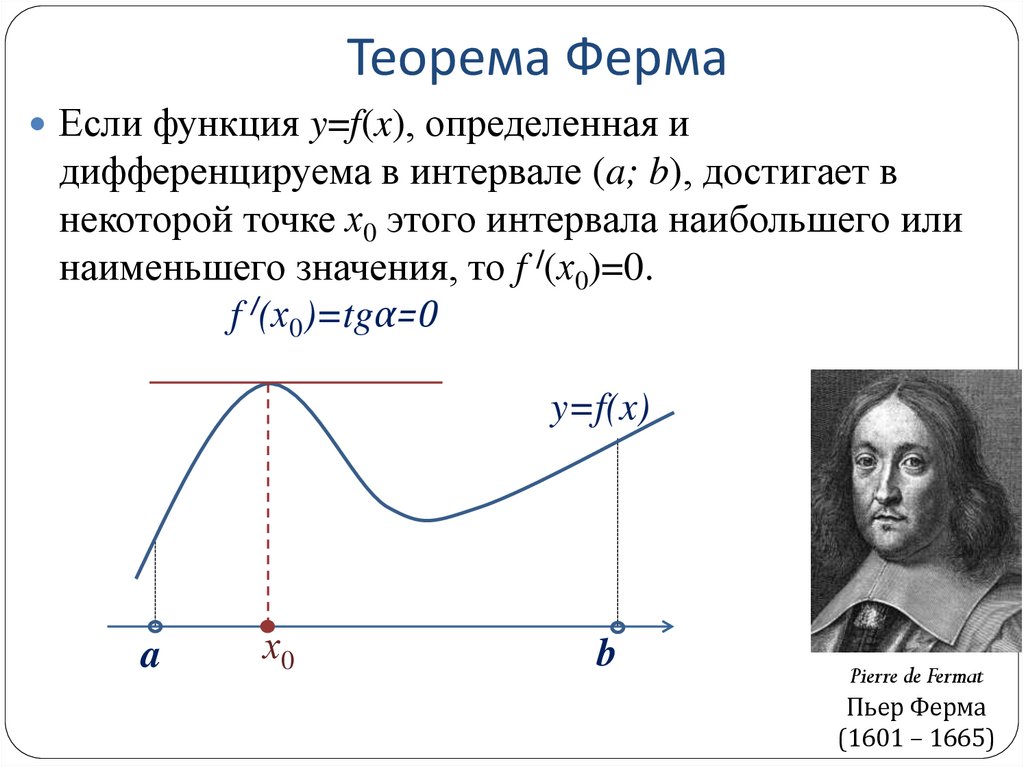
2. Теорема Ферма
Если функция y=f(x), определенная идифференцируема в интервале (a; b), достигает в
некоторой точке х0 этого интервала наибольшего или
наименьшего значения, то f /(х0)=0.
f /(х0)=tgα=0
y=f(x)
a
х0
b
Pierre de Fermat
Пьер Ферма
(1601 – 1665)
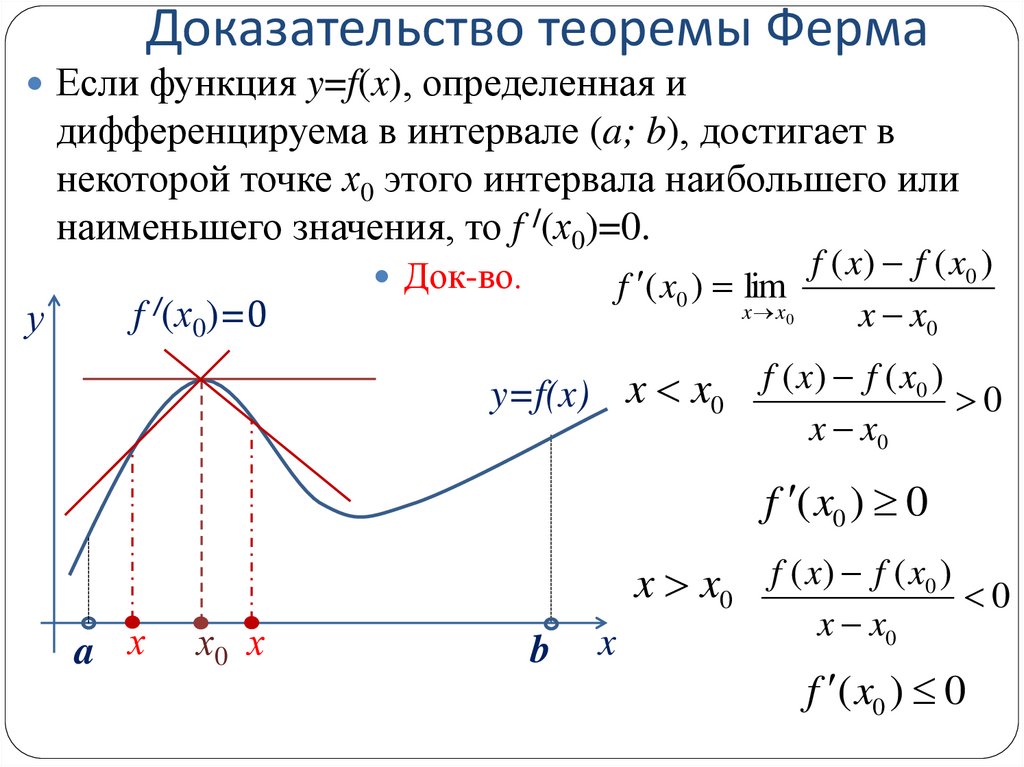
3. Доказательство теоремы Ферма
Если функция y=f(x), определенная идифференцируема в интервале (a; b), достигает в
некоторой точке х0 этого интервала наибольшего или
наименьшего значения, то f /(х0)=0.
у
f ( x) f ( x0 )
f ( x0 ) lim
x x0
x x0
Док-во.
f /(х0)=0
y=f(x) x x0 f ( x) f ( x0 ) 0
x x0
f ( x0 ) 0
x x0 f ( x) f ( x0 ) 0
a х
х0 х
b
x
x x0
f ( x0 ) 0
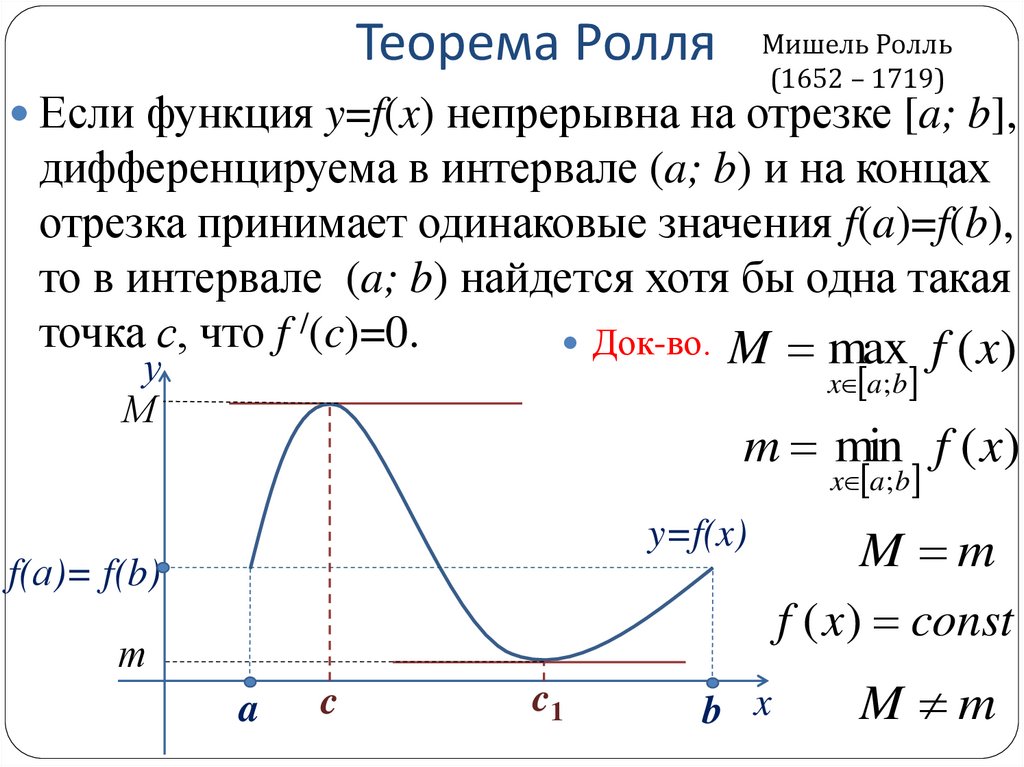
4. Теорема Ролля
Мишель Ролль(1652 – 1719)
Если функция y=f(x) непрерывна на отрезке [a; b],
дифференцируема в интервале (a; b) и на концах
отрезка принимает одинаковые значения f(a)=f(b),
то в интервале (a; b) найдется хотя бы одна такая
точка с, что f /(c)=0.
Док-во. M max f ( x)
у
М
x a ; b
m min f ( x)
x a ; b
y=f(x)
M m
f ( x) const
b x
M m
f(а)= f(b)
т
a
c
c1
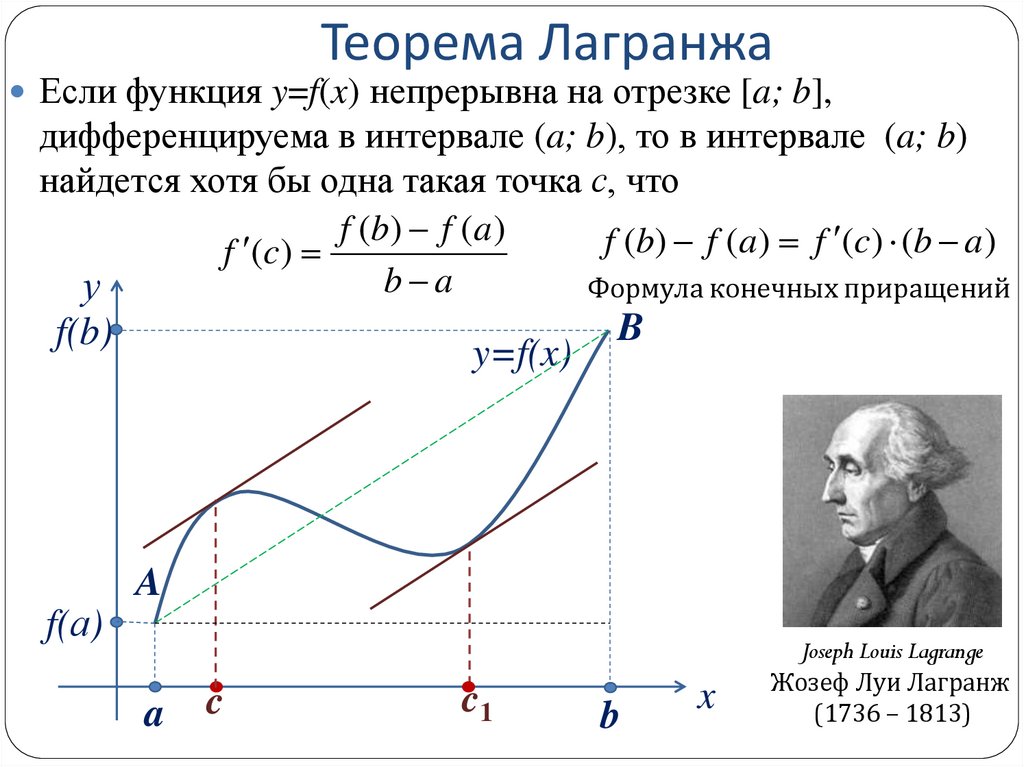
5. Теорема Лагранжа
Если функция y=f(x) непрерывна на отрезке [a; b],дифференцируема в интервале (a; b), то в интервале (a; b)
найдется хотя бы одна такая точка с, что
f (b) f (a )
f (b) f (a) f (c) (b a)
f (c)
b a
Формула конечных приращений
у
f(b)
y=f(x)
B
A
f(а)
a
c
c1
b
x
Joseph Louis Lagrange
Жозеф Луи Лагранж
(1736 – 1813)
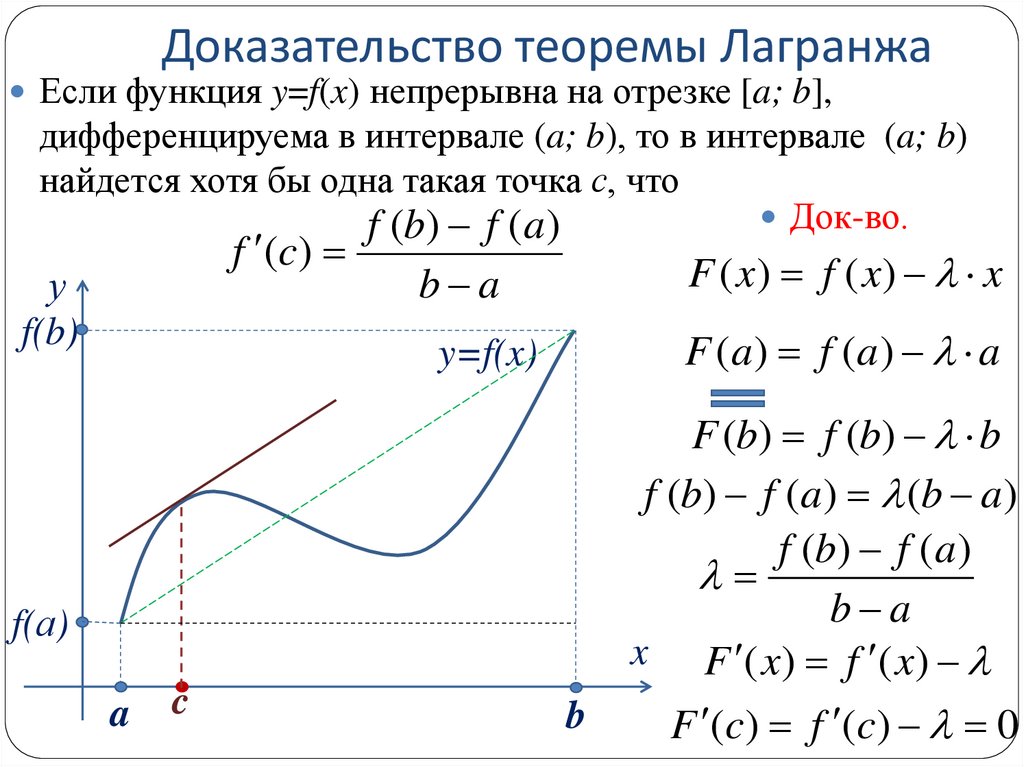
6. Доказательство теоремы Лагранжа
Если функция y=f(x) непрерывна на отрезке [a; b],дифференцируема в интервале (a; b), то в интервале (a; b)
найдется хотя бы одна такая точка с, что
Док-во.
f (b) f (a )
f (c)
у
f(b)
b a
F ( x) f ( x) x
y=f(x)
F (a) f (a) a
f(а)
a
c
b
F (b) f (b) b
f (b) f (a) (b a)
f (b) f (a )
b a
x F ( x) f ( x)
F (c) f (c) 0
7. Следствия из теоремы Лагранжа
Если производная функции равна нулю нанекотором промежутке, то функция постоянна на
этом промежутке:
x (a; b) f ( x) 0 f ( x) const
Если две функции имеют равные производные на
некотором промежутке, то они отличаются друг
от друга на постоянное слагаемое:
x (a; b) f ( x) g ( x) f ( x) g ( x) const
8. Теорема Коши
Если функции y=f(x) и y=g(x) непрерывны на отрезке[a; b], дифференцируемы в интервале (a; b), причем в
этих точках g/(x)≠0, то в интервале (a; b) найдется
хотя бы одна такая точка с, что
f (c) f (b) f (a)
g (c) g (b) g (a)
g (b) g (a) 0
Если бы g(b)=g(a), то по теореме Ролля в
интервале (a; b) существовала хотя бы
одна точка с, что g/(c)=0
Док-во.
F ( x) f ( x) g ( x)
f (b) f (a)
F ( x) f ( x)
g ( x)
g (b) g (a)
Augustin Louis Cauchy
Огюстен Луи Коши
(1789 – 1857)
9. Многочлен Тейлора
Brook TaylorБрук Тейлор
(1685 – 1731)
Многочлен Тейлора
Многочлен n-й степени:
Pn ( x) b0 b1 x b2 x ... bn x , bn 0, bi R
2
n
Разложение многочлена Рп(х) по степеням (х – х0):
Pn ( x) a0 a1 ( x x0 ) a2 ( x x0 ) ... an ( x x0 )
2
a0 Pn ( x0 )
(n)
Pn ( x0 )
an
n!
1
a2 Pn ( x0 )
2
a1 Pn ( x0 )
n
(k )
Pn ( x0 )
k
Pn ( x)
( x x0 )
k!
k 0
n
10. Теорема (формула) Тейлора
Функция f(x), дифференцируемая (n+1) раз внекоторой окрестности точки х0, может быть
представлена в виде суммы многочлена n-й степени
и остаточного члена Rn:
( n)
f ( x0 )
f ( x0 )
f
( x0 )
2
f ( x) f ( x0 )
( x x0 )
( x x0 ) ...
( x x0 ) n Rn
1!
2!
n!
f ( n 1) (c)
Rn
( x x0 ) n 1
(n 1)!
c x0 ( x x0 )
Многочлен Тейлора
0 1
c ( x0 ; x)
Остаточный член в
форме Лагранжа
11. Формула Маклорена
x0 0f (0)
f (0) 2
f ( n ) (0) n
f ( x) f (0)
x
x ...
x Rn
1!
2!
n!
( n 1)
f
(c) n 1
Rn
x
(n 1)!
c (0; x)
Замечание
n 0
f (с)
f ( x) f ( x0 )
( x x0 )
1!
f ( x) f ( x0 ) f (c) ( x x0 )
f ( x) f ( x0 ) f ( x0 )( x x0 )
f ( x0 x) f ( x0 ) f ( x0 ) x
Colin Maclaurin
Колин Маклорен
(1698 – 1746)
x x0 x
12. Правило Лопиталя (И.Бернулли – Лопиталя)
Пусть функции f(x) и g(x) дифференцируемы внекоторой окрестности точки х0, за исключением, быть
может, самой этой точки, и пусть lim f ( x) lim g ( x) 0 или
x x
x x
lim f ( x) lim g ( x) . Тогда, если существует предел
x x0
x x0
f ( x)
отношения производных этих функций lim
, то
x x g ( x )
существует и предел отношения самих функций при
f ( x)
f ( x)
х→х0, причем
lim
lim
0
x x0 g ( x)
x x0 g ( x)
0
0
0
0
Guillaume François Antoine,
marquis de L'Hôpital
Гийом Франсуа Лопиталь
(1661 – 1704)
0
0
0
0
1







 mathematics
mathematics








