Лекция 5 Методы расчета переходных процессов в электрических цепях (1)

1. Лекция 5 Методы расчета переходных процессов в электрических цепях

1 Классический метод расчета
2 Операторный метод расчета
1. Литература: Горбунов А.Н. и др.
Теоретические основы электротехники. С.246291.
1

2. Классический метод расчета

Метод относится к линейным цепям с
сосредоточенными параметрами. Название
«классический» отражает использование в нем
решений дифференциальных уравнений с
постоянными параметрами методами классической
математики.
Особенности метода:
1) При решении задачи имеют дело с реальными
величинами и с реальным временем;
2) Результаты расчета обычно иллюстрируют
графиками;
3) Расчеты сложны и трудоемки, поэтому для их
выполнения эффективно применение
2
вычислительной техники.

3. Методика расчета

• составляют дифференциальные уравнения для мгновенных
значений токов и напряжений по законам Кирхгофа, Ома и
электромагнитной индукции.
• из системы уравнений получают неоднородное
дифференциальное уравнение с постоянными коэффициентами
для искомой неизвестной.
• Общее решение этого уравнения представляет собой сумму
двух составляющих: частного решения неоднородного
уравнения для установившегося режима и общего решения
однородного дифференциального уравнения для свободного
режима:
3

4.

• находят установившуюся составляющую путем расчета
электрической цепи после коммутации;
• находят свободную составляющую, которая зависит только от
характера цепи, то есть определяется видом корней pk
характеристического уравнения. Общее решение для свободной
составляющей процесса:
где Ak - постоянная интегрирования.
• Если характеристическое уравнение имеет два вещественных
корня, то
• Если корни характеристического уравнения комплексные
сопряженные вида
где - коэффициент затухания контура;
0 – угловая частота свободных колебаний.
4

5.

• определяют постоянные интегрирования по начальным
условиям.
- Начальные значения токов в ветвях с катушками определяют
по независимым начальным условиям, исходя из первого
закона коммутации:
iL(0+) = iL(0-).
- Начальные значения напряжения на конденсаторе определяют
исходя из второго закона коммутации:
uc(0+) = uc(0-).
- Начальные значения токов в других ветвях, не содержащих катушек, или напряжения на других элементах,
кроме
конденсаторов, определяют по законам Кирхгофа с
применением законов коммутации;
• находят переходные ток или напряжение путем суммирования установившейся и свободной составляющих;
• проверяют правильность полученного результата расчета
переходной функции определяя начальные и
установившиеся значения переходных параметров.
5

6. 1. Составляем систему уравнений, описывающих состояние цепи на основе II закона Кирхгофа, Закона Ома и закона электромагнитной

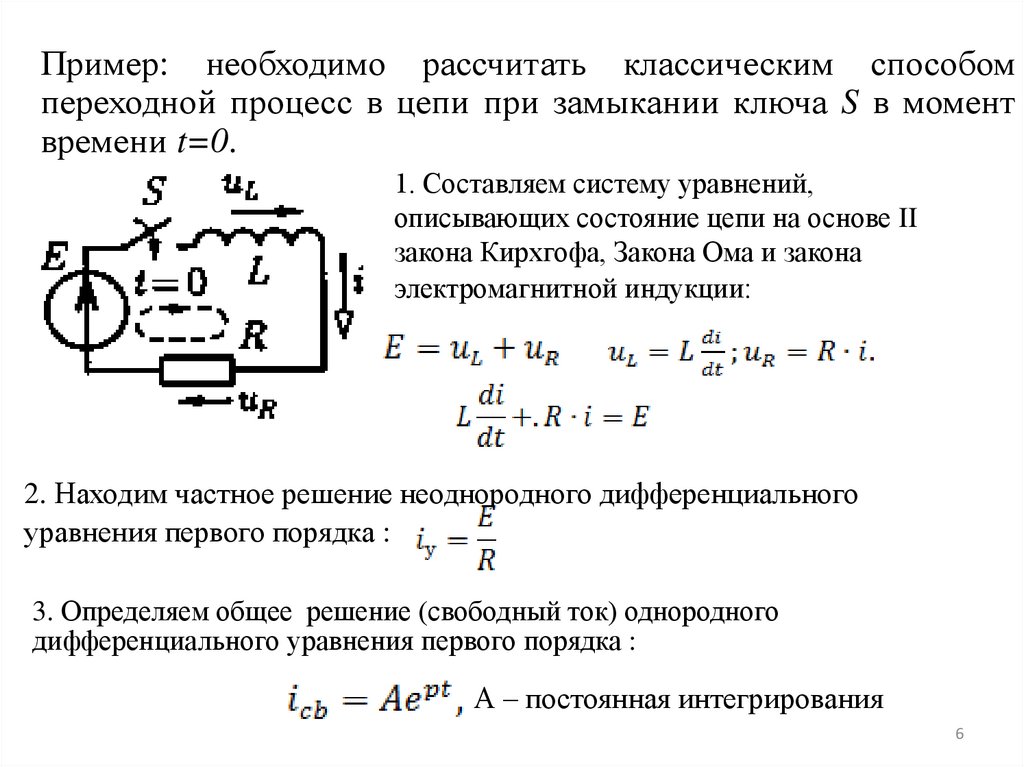
Пример: необходимо рассчитать классическим способом
переходной процесс в цепи при замыкании ключа S в момент
времени t=0.
1. Составляем систему уравнений,
описывающих состояние цепи на основе II
закона Кирхгофа, Закона Ома и закона
электромагнитной индукции:
2. Находим частное решение неоднородного дифференциального
уравнения первого порядка :
3. Определяем общее решение (свободный ток) однородного
дифференциального уравнения первого порядка :
А – постоянная интегрирования
6

7.

4. Определяем общее решение (переходной ток) однородного дифференциального
уравнения первого порядка :
5. Определяем постоянную интегрирования А:
При t=0 i(0+) = i(0-)=0
6 . Находим выражение для переходного тока:
7

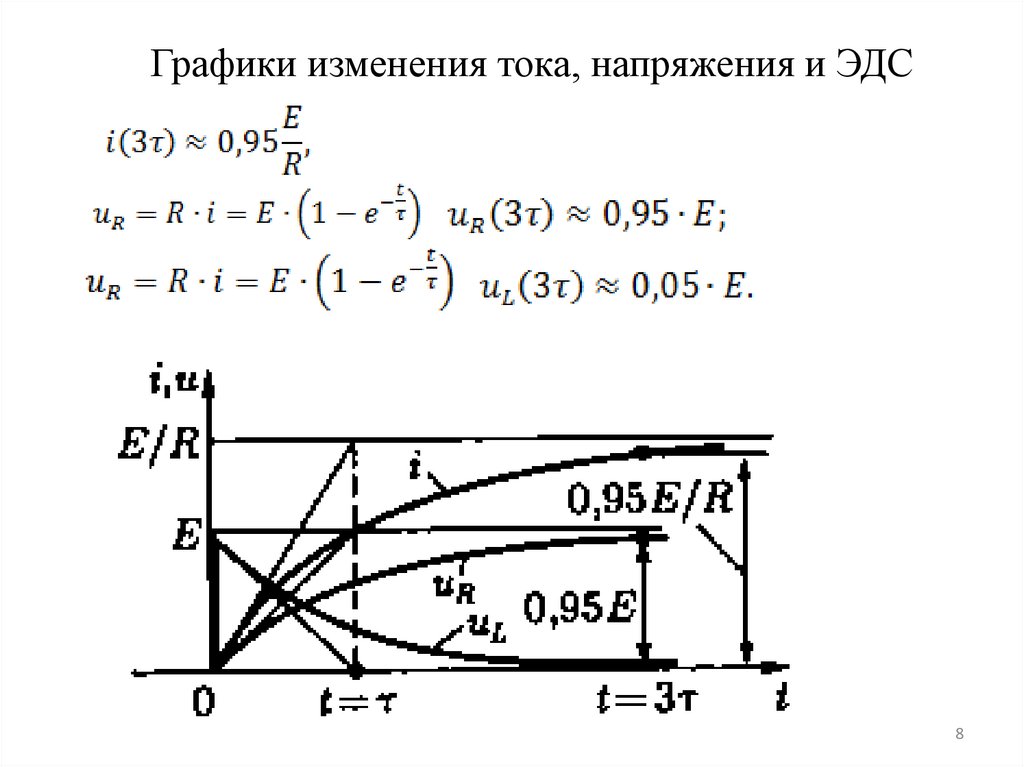
8. Графики изменения тока, напряжения и ЭДС

8

9. Операторный метод

Идея метода заключается в том, что расчет переходного
процесса переносится из области функций действительной
переменной (времени t) в область функций комплексной
переменной p, в которой дифференциальные уравнения
преобразуются в алгебраические.
Такое преобразование называется прямым.
Полученное решение алгебраических уравнений
обратным преобразованием переносится в область
действительной переменной.
Прямое преобразование Лапласа:
f(t) – оригинал; F(p) – изображение Лапласа;
p =ϭ+jω –комплексная переменная;
L – знак прямого преобразования Лапласа.
9

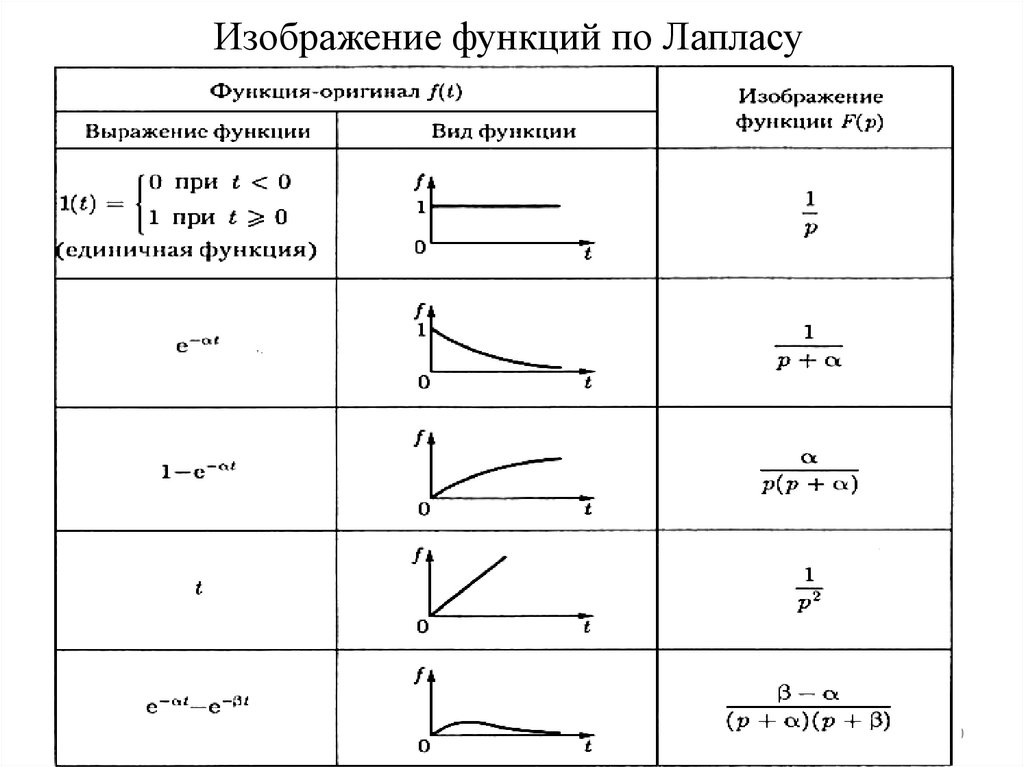
10. Изображение функций по Лапласу

10

11. Законы Ома в операторной форме

.
• Для
резистивного элемента:
• Для индуктивности:
• Для емкости:
11

12. Законы Кирхгофа в операторной форме

Первый закон Кирхгофа: алгебраическая сумма изображений токов в
узле электрической цепи равна нулю:
Второй закон Кирхгофа: в любом контуре электрической цепи
алгебраическая сумма изображений ЭДС источников равна
алгебраической сумме изображений падений напряжений на элементах
этого контура:
12

13. Методика расчета переходных процессов операторным методом

1. Представить исходные данные о параметрах всех элементов
схемы цепи в операторной форме (e(t) →E(p), u(t)→U(p),
i(t)→I(p), а пассивные элементы – схемами замещения.
2. Для полученной схемы замещения в операторной форме
составить и решить систему независимых уравнений по I и II
законам Кирхгофа в операторной форме, т.е. найти, например,
ток I(p).
3. Если изображение имеет вид рациональной дроби
для нахождения оригинала f(t) необходимо воспользоваться
теоремой разложения
13