02 Последовательности

1.

[Числовая] последовательность – функция, определенная на множестве и
принимающая числовые значения.
Сокращенно последовательность x1 , x2 ,..., xn ,... обозначается символом xn .
Если n1 n2 ... nk ... – возрастающая последовательность натуральных
чисел, то последовательность xn1 , xn2 ,..., xnk ,... называется подпоследовательностью последовательности xn .
Арифметические операции над последовательностями:
df
xn yn x1 y1 , x2 y2 , ..., xn yn , ... ;
df
xn yn x1 y1 , x2 y2 , ..., xn yn , ... ;
df
xn yn xn yn x1 y1 , x2 y2 , ..., xn yn , ... ;
xn df x1 x2
xn
,
,
...,
, ... , если n yn 0 .
y
y
y
y
1
2
n
n
1

2.

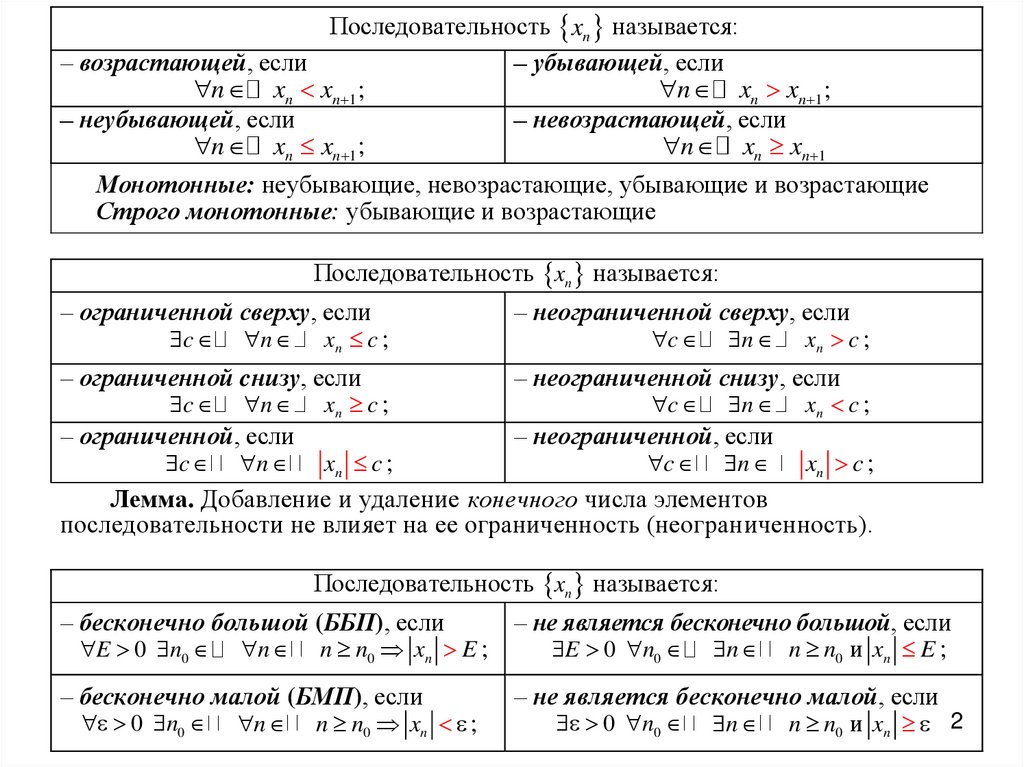
Последовательность xn называется:
– возрастающей, если
– убывающей, если
n xn xn 1 ;
n xn xn 1 ;
– неубывающей, если
– невозрастающей, если
n xn xn 1 ;
n xn xn 1
Монотонные: неубывающие, невозрастающие, убывающие и возрастающие
Строго монотонные: убывающие и возрастающие
Последовательность xn называется:
– ограниченной сверху, если
– неограниченной сверху, если
– ограниченной cнизу, если
– неограниченной снизу, если
– ограниченной, если
– неограниченной, если
c
c
c
n
n
n
xn c ;
xn c ;
xn c ;
c
n
c
n
c
n
xn c ;
xn c ;
xn c ;
Лемма. Добавление и удаление конечного числа элементов
последовательности не влияет на ее ограниченность (неограниченность).
Последовательность xn называется:
– бесконечно большой (ББП), если
– не является бесконечно большой, если
E 0 n0 n n n0 и xn E ;
– бесконечно малой (БМП), если
– не является бесконечно малой, если
E 0 n0
0 n0
n
n
n n0 xn E ;
n n0 xn ;
0 n0
n
n n0 и xn 2

3.

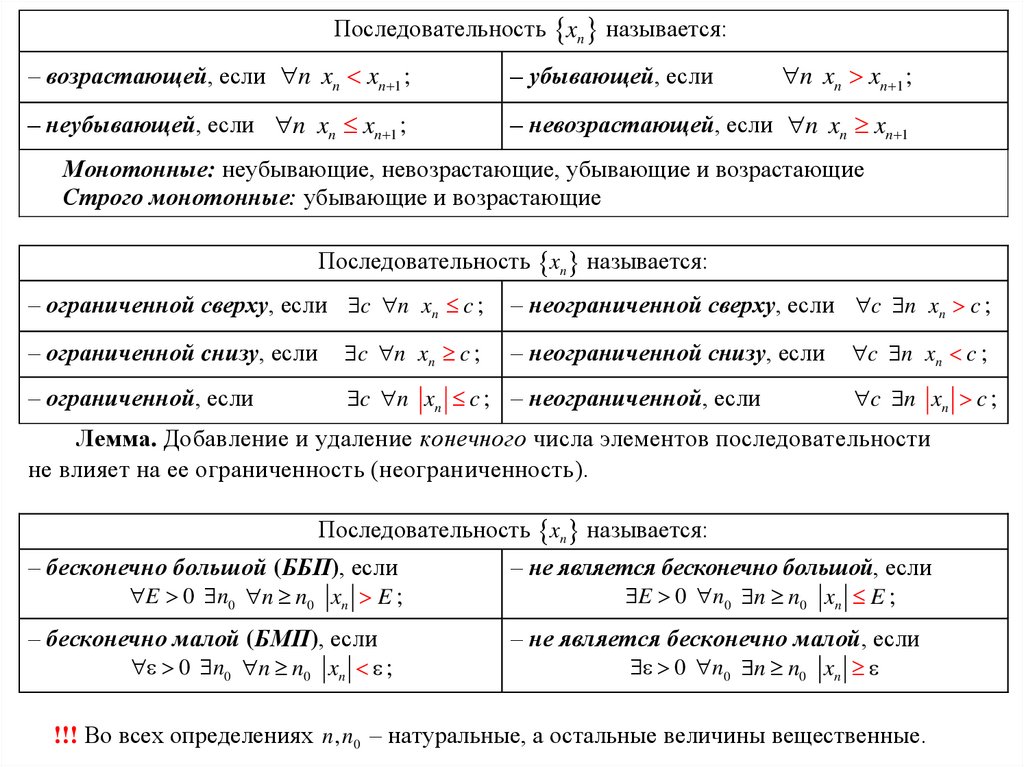
Последовательность xn называется:
– возрастающей, если n xn xn 1 ;
– убывающей, если
n xn xn 1 ;
– неубывающей, если n xn xn 1 ;
– невозрастающей, если n xn xn 1
Монотонные: неубывающие, невозрастающие, убывающие и возрастающие
Строго монотонные: убывающие и возрастающие
Последовательность xn называется:
– ограниченной сверху, если c n xn c ;
– неограниченной сверху, если c n xn c ;
– ограниченной cнизу, если
c n xn c ;
– ограниченной, если
c n xn c ; – неограниченной, если
– неограниченной снизу, если
c n xn c ;
c n xn c ;
Лемма. Добавление и удаление конечного числа элементов последовательности
не влияет на ее ограниченность (неограниченность).
Последовательность xn называется:
– бесконечно большой (ББП), если
E 0 n0 n n0 xn E ;
– не является бесконечно большой, если
E 0 n0 n n0 xn E ;
– бесконечно малой (БМП), если
– не является бесконечно малой, если
0 n0 n n0 xn ;
0 n0 n n0 xn
!!! Во всех определениях n, n0 – натуральные, а остальные величины вещественные.
3

4.

Точные грани последовательностей
Если xn ограниченная последовательность, то
1) n
xn s ;
s sup xn sup xn 2) 0 n xn s
n
или s s n s xn .
1) n i x ;
n
i inf xn inf xn 2) 0 n xn i
n
или i i n xn i .
Если xn неограничена сверху, то sup xn .
Если xn неограничена снизу, то inf xn .
4

5.

СВОЙСТВА БЕСКОНЕЧНО МАЛЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
1. БМП ограничена.
2. Если xn БМП, то xn БМП, и наоборот.
3. Если xn и yn – БМП, то
а) xn yn – БМП;
б) c
cxn – БМП.
Следствие. Алгебраическая сумма любого конечного
числа БМП есть БМП.
4. Произведение БМП на ограниченную посл-ть есть БМП.
Следствие. Произведение любого числа БМП есть БМП.
5. Если все элементы БМП равны, то их значение 0.
1
6. Если xn ББП (БМП) и n xn 0 , то БМП (ББП).
xn
7. Если xn БМП и n yn xn , то yn БМП.
5

6.

ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
Посл-ть xn называется сходящейся, если существует такое число a , называ-
емое пределом посл-ти xn , что выполняется любое из следующих утверждений:
1) 0 n0 n0
n
2) xn a – БМП;
n n0 xn a ;
3) в любой -окрестности числа a находятся все элементы посл-nи xn ,
начиная с некоторого номера.
Обозначение:
lim xn a
n
или
xn a при n .
Основное свойство последовательностей. Конечное число элементов
(их добавление или удаление) не влияет на сходимость посл-ти, причем значение
предела сходящейся посл-ти остается неизменным.
Число a не является пределом посл-ти xn , если выполняется любое
из следующих утверждений:
1) 0 n0 n
n n0 и xn a .
2) существует окрестность числа a , вне которой находится бесконечно много
членов посл-ти.
8

7.

Если нельзя подобрать число a , удовлетворяющее одному из определений предела, т.е.
a 0 n0 n n n0 и xn a ,
то посл-ть называют расходящейся.
!!! Все неограниченные посл-ти расходятся.
!!! Существуют расходящиеся ограниченные посл-ти.
ББП иногда называют посл-тями, сходящимися к бесконечности
(или посл-тями, имеющими бесконечный предел):
lim xn
0 n0 n0 n n n0 xn ;
lim xn
0 n0 n0 n n n0 xn ;
lim xn
0 n0 n0 n n n0 xn .
n
n
n
!!! Все ББП являются неограниченными, но существуют неограниченные посл-ти, которые не являются ББП.
!!! ББП к сходящимся посл-nям не относят, т.е. всякая ББП расходится.
!!! Во всех определениях n n0 можно заменить на n n0 .
9

8.

СВОЙСТВА СХОДЯЩИХСЯ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
1. Сходящаяся последовательность имеет только один предел.
2. Сходящаяся последовательность ограничена.
1
3. Если lim xn p , p 0 и n xn 0 , то посл-ть ограничена.
n
xn
4. Пусть lim xn a , lim yn b . Тогда
n
n
а) lim xn yn a b ; в) lim xn yn a b ;
n
n
x a
б) lim xn yn a b ; г) если n yn 0 и b 0 , то lim n .
n y
n
n b
5. Если lim xn p и
n
а) n xn c , то p c ;
б) n xn c , то p c ;
в) n xn a , b , то p a , b ;
г) n xn a, b , то p a , b .
Замечание. Даже если все элементы сходящейся посл-ти xn будут удовлетворять строгому неравенству xn c ( xn c ), предел p может оказаться равным c .
6. Пусть lim xn a , lim yn b . Если n n n0 xn yn (или xn yn ), то a b .
n
n
7. Теорема о трех последовательностях.
a.
Пусть lim xn a , lim yn a , a . Если n n n0 xn zn yn , то lim zn 10
n
n
n

9.

СВОЙСТВА БЕСКОНЕЧНО БОЛЬШИХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
1. lim xn тогда и только тогда, когда lim xn .
n
n
2. Пусть c 0 . Если, начиная с некоторого номера,
а) lim yn и n0 n n0 xn cyn , то lim xn ;
n
n
б) lim yn и n0 n n0 xn cyn , то lim xn ;
n
n
в) lim yn и n0 n n0 xn cyn , то lim xn .
n
n
3. Пусть lim xn s , s , . Если
n
а) n0 n n0 yn c 0 , то lim xn yn s ;
n
б) n0 n n0 yn c 0 , то lim xn yn s .
n
4. Если lim xn и n0 n n0 yn c 0 , то lim xn yn .
n
n
5. Если yn ограничена
а) снизу и lim xn , то lim xn yn .
n
n
б) свеху и lim xn , то lim xn yn .
n
n
16

10.

Теорема Вейерштрасса о пределе монотонной последовательности.
Если посл-ть монотонна и ограничена, то она имеет конечный предел.
З а м е ч а н и е . Теорема остается справедливой, если xn монотонна,
начиная с некоторого номера.
n
1
Теорема. Последовательность xn 1 сходится.
n
З а м е ч а н и е . Предел этой посл-ти называют постоянной Эйлера и
обозначают буквой e : e 2.718281828459045 .
Теорема Штольца о пределе частного. Пусть
а) xn строго монотонна;
б) xn и yn являются одновременно либо БМП, либо ББП;
yn yn 1
в) существует конечный или бесконечный предел lim
.
n x x
n
n 1
y
y yn 1
Тогда существует предел lim n lim n
.
Пример
n x
n x x
n
n
n 1
З а м е ч а н и е . Теорема остается справедливой, если xn строго монотонна, начиная с некоторого номера.
17

11.

ПОДПОСЛЕДОВАТЕЛЬНОСТИ.
ЧАСТИЧНЫЙ ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
– подпосл-ть посл-ти x и lim x S , где S – число
Если xnk
n
k
nk
или одна из бесконечностей , , то S называют частичным
пределом посл-ти xn .
Число i lim inf xk ( s limsup xk ) называется нижним (верхним)
n k n
n k n
пределом посл-ти xn и обозначается lim xk ( lim xk )
k
df
lim xk lim inf xk ,
k
n k n
k
df
lim xk limsup xk .
k
n k n
З а м е ч а н и е . В общем случае, значения lim xn и inf xn , а также
n
lim xn и sup xn не совпадают.
n
21

12.

Лемма Больцано-Вейерштрасса об ограниченной посл-ти. Каждая
ограниченная числовая посл-ть содержит сходящуюся подпосл-ть.
Лемма о неограниченной посл-ти. Всякая неограниченная посл-ть
имеет частичный предел, равный либо , либо .
Следствие. Из каждой посл-ти действительных чисел можно
извлечь сходящуюся подпосл-ть или подпосл-ть, стремящуюся
к бесконечности.
! ! ! Посл-ть может быть ограниченной (а значит, иметь сходящуюся
подпосл-ть), но не иметь предела.
! ! ! Посл-ть может иметь частичный бесконечный предел, но не
являться ББП.
22

13.

Свойства нижних и верхних пределов
1. Для любых последовательностей xk и yk :
lim xk lim yk lim xk yk lim xk yk lim xk lim yk .
k
k
k
k
k
k
2. Для любых последовательностей xk и yk с неотрицательными членами:
lim xk lim yk lim xk yk lim xk yk lim xk lim yk .
k
k
k
k
k
k
3. Для произвольной последовательности xk
inf xk lim xk lim xk sup xk .
k
k
xk 1
xk 1
k
k
lim xk lim xk lim
4. Если k xk 0 , то lim
.
k
k
k xk
k
xk
25

14.

ФУНДАМЕНТАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ (ФП)
Посл-ть xn называется фундаментальной (или посл-тью Коши), если
0 n0 n n0 m n0 xn xm
или, что то же самое,
0 n0 n n0 k xn k xn .
З а м е ч а н и е . Неравенства n n0 , m n0 можно заменить неравенствами
n n0 , m n0 .
Свойства фундаментальных последовательностей
1. Всякая фундаментальная посл-ть ограничена.
2. Всякая сходящаяся последовательность фундаментальна.
3. Любая подпосл-ть ФП фундаментальна.
4. Если подпосл-ть ФП сходится к A , то и сама посл-ть сходится к A.
5. Если xn – ФП, то xn – ФП.
6. Если xn , yn – ФП, то xn yn – ФП.
26

15.

Критерий Коши сходимости последовательности
Числовая посл-ть сходится тогда и только тогда, когда она ФП.
Необходимость. Совпадает со свойством 2.
Достаточность. Пусть xn – ФП. Тогда, в силу свойства 1, она
ограничена. По лемме Больцано-Вейерштрасса ограниченная посл-ть
содержит сходящуюся подпосл-ть
x , а значит, по свойству 4, сама
nk
посл-ть xn тоже сходится.
Следствие (критерий Коши расходимости последовательности).
Числовая посл-ть рассходится тогда и только тогда, когда она не ФП, т.е.
0 n0 n n0 m n0 и xn xm
или
0 n0 n n0 k xn k xn .
31

16.

ОТКРЫТЫЕ И ЗАМКНУТЫЕ МНОЖЕСТВА
Точка x0 называется предельной точкой множества X , если
0 x X , x x0 x x0 .
!!! Предельная точка может как принадлежать, так и не принадлежать X .
Символ называют предельной точкой (предельным значением) X , если
x X x E x E .
Точка x0 X называется изолированной точкой множества X , если
E
0 x X x x0 x x0 , x0 .
Точка x0
называется:
x x x X ;
x x x X ;
– внутренней точкой множества X , если 0 x
– внешней точкой множества X , если 0 x
0
0
– граничной точкой множества X , если она не является ни внутренней, ни внешней, т.е.
0 x1 X x1 x0 x2 X x2 x0 .
Множество всех граничных точек множества X называется границей множества X .
! ! ! Всякая внутренняя точка является предельной.
! ! ! Всякая изолированная точка является граничной.
! ! ! Всякая граничная точка не является внутренней.
Множество X называется открытым, если все его точки внутренние.
Множество X называется замкнутым, если оно содержит все точки своей границы или,
что то же самое, все свои предельные точки.
! ! ! Множества
и являются и открытыми и замкнутыми одновременно.
32