Занятие 1 n

1. Раздел 1 Алгебра и геометрия

2. Лекция 1

Учебные вопросы
1. Понятие матрицы.
2. Определители 2-го и 3-го порядка.
3. Свойства определителей.

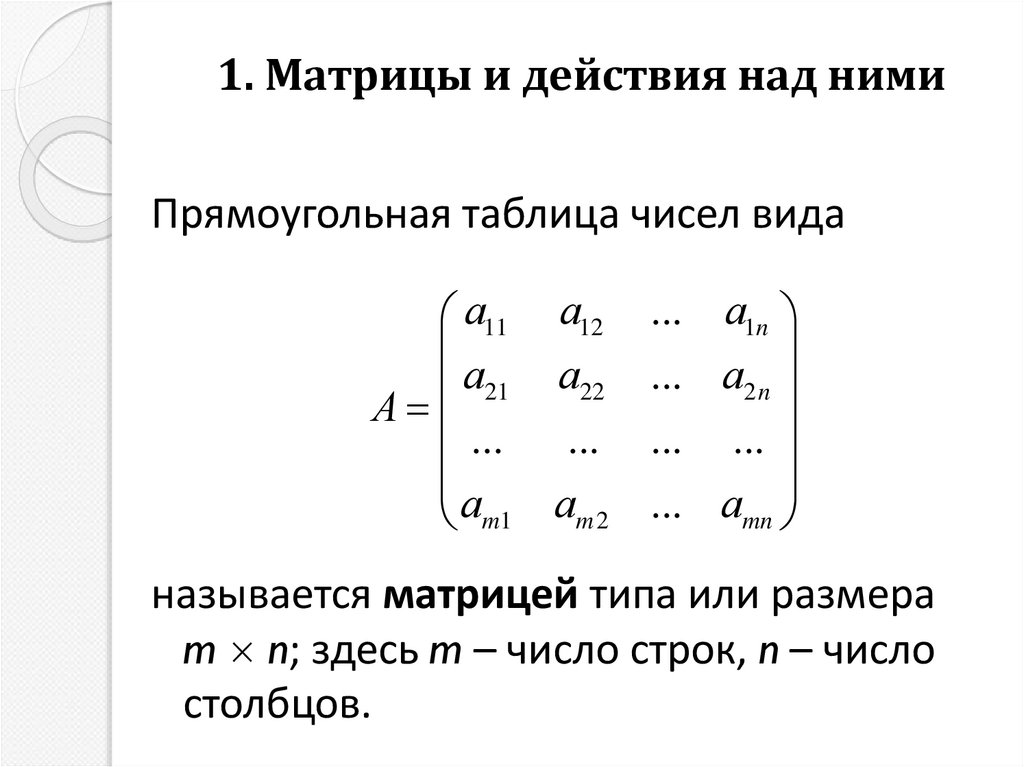
3. 1. Матрицы и действия над ними

Прямоугольная таблица чисел вида
а11 а12
а
а22
21
А
... ...
а
m1 аm 2
... а1n
... а2 n
... ...
... аmn
называется матрицей типа или размера
m n; здесь m – число строк, n – число
столбцов.

4. 1. Матрицы и действия над ними

Если число строк и столбцов матрицы
одинаковое , то матрица называется
квадратной, порядка n.
Квадратная матрица, в которой все
элементы, не стоящие на главной
диагонали, равны нулю, называется
диагональной, например:
3 0 0
0 1 0
0 0 5

5. 1. Матрицы и действия над ними

Диагональная матрица, у которой все
элементы,
стоящие
на
главной
диагонали равны единице, называется
единичной, например
1 0 0
0 1 0
0 0 1
- единичная матрица 3-го порядка.

6. 1. Матрицы и действия над ними

Прямоугольная матрица, в которой
каждая строка заменена столбцом с
тем
же
номером,
называется
транспонированной по отношению к
Т
A
данной матрице, обозначается .
Например, если
1 4 5
1 2 3
A 2 3 7 то AT 4 3 6 .
3 6 8
5 7 8
Т
Т
Очевидно: А А

7. 1. Матрицы и действия над ними

Суммой двух матриц одинакового
типа называется матрица того же типа,
все элементы которой равны суммам
соответствующих элементов слагаемых
матриц.
Пример
5 4 1 3 6 5 8 10 4
2 6 3 2 1 3 0 7 0

8. 1. Матрицы и действия над ними

Произведением матрицы А на
число α называется матрица αА или
Аα, все элементы которой равны
соответствующим элементам матрицы
А, умноженным на α.
Пример
1 1 0 3 3 0
3 2 0 3 6 0 9
3 2 2 9 6 6

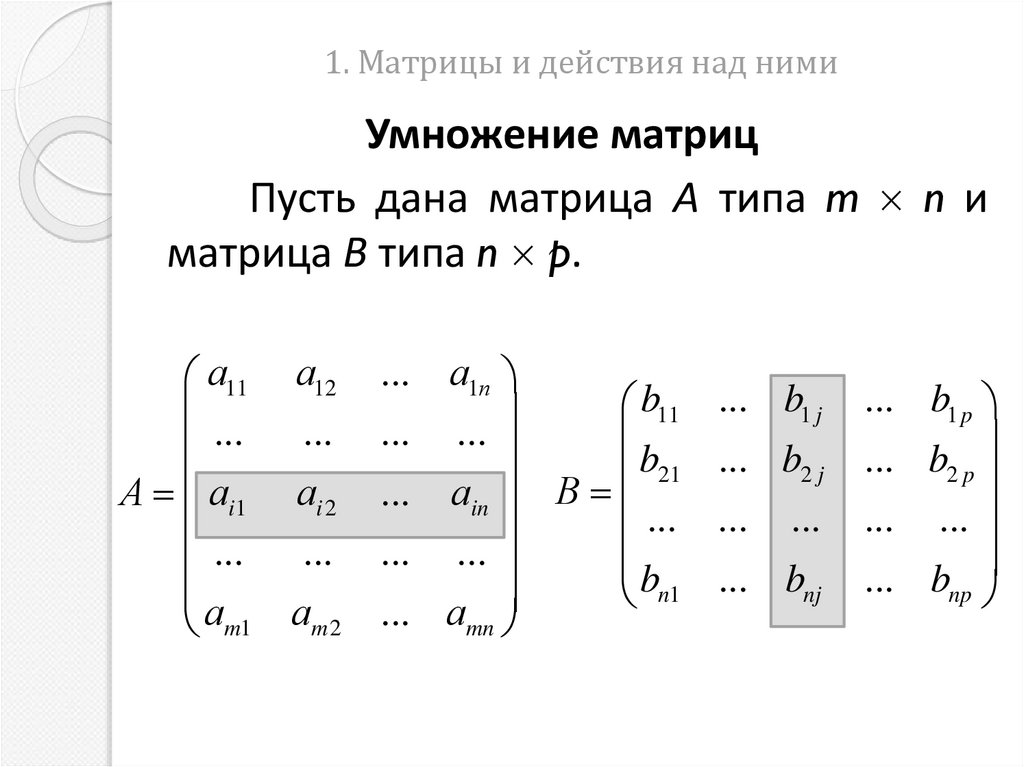
9. 1. Матрицы и действия над ними

Умножение матриц
Пусть дана матрица А типа m n и
матрица В типа n p.
а11 а12
... ...
А аi1 аi 2
... ...
а
m1 аm 2
... а1п
b11
... ...
b
21
... аin В
...
... ...
b
n1
... amn
... b1 j
... b2 j
... ...
... bnj
... b1 p
... b2 p
... ...
... bnp

10. 1. Матрицы и действия над ними

Для таких двух матриц, у которых число
столбцов первой равно числу строк второй,
определено понятие произведения матрицы
А на В следующим образом: С = А · В , где С
есть матрица типа m p
с11 с12 ... с1 p
с
с
...
с
21
22
2p
C
... ... ... ...
сm1 сm 2 ... сmp
где cij ai1b1 j ai 2b2 j ... ainbnj ,
i 1,2, , m; j 1,2, , p .

11. 1. Матрицы и действия над ними

A B
= C
( m n) ( n p ) ( m p )
2 1
1 3
3
2
8
1
Пример 1
1 4 0 3 0 1
3 1
3 2 2 1 8 0 1 3
3 1 2 3 8 1 1 1
1 2 4 1 0 0 3 3 1 1 4 3 0 1 3 1
11 0
7 14

12. 1. Матрицы и действия над ними

Произведение двух матриц, вообще
говоря, НЕ коммутативно:
.
AB BA
Пример 2
4 2
12 20 34
3 4 5
.
BA 7 1
21
30
42
0 2 7
9 3
27 42 66
4 2
12 20 34
3 4 5
.
BA 7 1
21
30
42
0 2 7
9 3
27 42 66

13. Определители 2-го и 3-го порядка

Рассмотрим квадратную матрицу 2-го
порядка:
a11 a12
A
a21 a22
Определение. Определителем 2-го
порядка, соответствующим матрице А,
называется число
a11 a12
det A
a11 a22 a12 a21
a21 a22

14. Определители 2-го и 3-го порядка

Числа а11, а12, а21, а22 называются
элементами определителя (они же
элементы матрицы А).
Элементы а11, а22 составляют
главную диагональ, а элементы а21,
а12 – побочную диагональ.
a11 a12
det A
a21 a22

15. Определители 2-го и 3-го порядка

Пусть дана квадратная матрица 3-го
порядка
a11 a12 a13
A a21 a22 a23
a
a
a
33
31 32

16. Определители 2-го и 3-го порядка

Определение. Определителем 3-го
порядка, соответствующим матрице
А, называется число , которое
определяется выражением:
a11 a12
det A a21 a22
a31 a32
a13
a23
a33
a11a22 a33 a21a32 a13 a12 a23a31 a13a22a31 a12a21a33 a23a32a11.

17. Определители 2-го и 3-го порядка

Определитель 2-го порядка
вычисляется по определению:
a11 a12
det A
a11 a22 a12 a21
a21 a22
Пример
2 5
2 7 5 3 14 15 29.
3 7

18. Определители 2-го и 3-го порядка

Для вычисления определителя 3-го
порядка можно воспользоваться
следующими правилами:
Правило Саррюса
_
a11 a12
a21 a22
a31 a32
_
_
a13 a11 a12
a23 a21 a22
a33 a31 a32
+
+
+

19. Определители 2-го и 3-го порядка

Пример
Вычислить
1 2 1
3 1 2
4 2 5
Решение
1 2 1 1 2
3 1 2 3 1
4 2 5 4 2
1 1 5 2 2 4 ( 1) 3 ( 2)
1 1 4 1 2 2 2 3 5 5

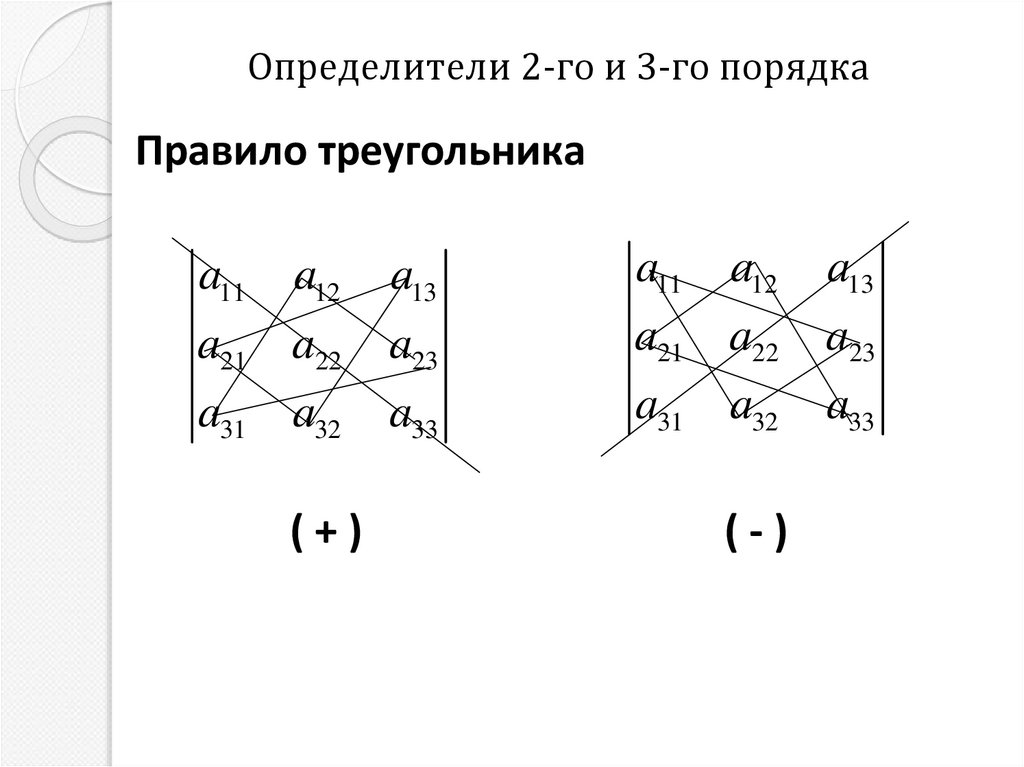
20. Определители 2-го и 3-го порядка

Правило треугольника
a11 a12
a21 a22
a31 a32
(+)
a13
a23
a33
a11 a12
a21 a22
a31 a32
(-)
a13
a23
a33

21. Определители 2-го и 3-го порядка

Пример
Вычислить
Решение
3 2 1
2
2
1
0
3 2 1
2 1 3
2 0 2
3 3 1 2 2 3 2 2 0 1
2
1 1 2 3 0 3 2 2 2
6 12 0 2 0 8 12

22. Определители 2-го и 3-го порядка

Рассмотрим определитель 3-го порядка:
a11 a12 a13
a21 a22 a23
a31 a32 a33
Минором некоторого элемента
определителя называется определитель,
полученный
из
данного
путем
вычеркивания строки и столбца, на
пересечении которых стоит этот элемент.
Обозначение минора M aij

23. Определители 2-го и 3-го порядка

Алгебраическим дополнением любого
элемента определителя называется минор
этого элемента, взятый со своим знаком,
если сумма номеров строки и столбца, на
пересечении которых стоит этот элемент,
есть
число
четное,
либо
с
противоположным знаком, если эта сумма
есть
число
нечетное.
Обозначение
алгебраического дополнения Aij .

24. Определители 2-го и 3-го порядка

Рассмотрим определитель
a11 a12 a13
a21 a22
a31 a32
a23
a33
Минор элемента a12 :
a21 a23
M a12
a21 a33 a23 a31
a31 a33
Алгебраическое дополнение элемента a12 :
a21 a23
A12
a21 a33 a23 a31.
a31 a33

25. Определители 2-го и 3-го порядка

Свойства определителей
1. Определитель равен сумме
произведений элементов какого-нибудь
столбца (или строки) на их алгебраические
дополнения.
Пример
1 2 3
5 6
4 6
4 5
4 5 6 1
2
3
8 9
7 9
7 8
7 8 9
45 48 2 36 42 3 32 35 0

26. Определители 2-го и 3-го порядка

2. Величина определителя не
изменится, если каждую его строку
заменить столбцом с тем же номером.
3. Перестановка двух столбцов или
двух строк определителя равносильна его
умножению на (–1).
4. Общий множитель всех элементов
одного столбца или одной строки
определителя можно вынести за знак
определителя.

27. Определители 2-го и 3-го порядка

5. Если все элементы какой-либо
строки или какого-либо столбца равны
нулю, то определитель равен нулю.
6. Определитель, имеющий два
одинаковых столбца или две одинаковых
строки, равен нулю.
7. Определитель равен нулю, если
элементы двух столбцов или двух строк
пропорциональны.

28. Определители 2-го и 3-го порядка

8. Если каждый элемент некоторой строки
(столбца) определителя представлен в виде
суммы двух слагаемых, то определитель равен
сумме двух определителей, у которых все строки
(столбцы), кроме данной, прежние, а в данной
строке (столбце) в первом определителе стоят
первые слагаемые, а во втором – вторые:
a11
a12
a11
a21
a22
a21
a31
a32
a31
a12
a13 a11
a22
a23 a21
a32
a33 a31
a12
a13 a11
a22
a23 a21
a32
a33 a31
a13
a23
a33

29. Определители 2-го и 3-го порядка

9. Если к элементам некоторого
столбца (или строки) определителя
прибавить соответствующие элементы
другого
столбца
(или
строки),
умноженные на общий множитель, то
величина определителя не изменится.
10. Сумма произведений элементов
какого-нибудь столбца (или строки) на
алгебраические дополнения элементов
другого столбца (или строки)
определителя равна нулю.

30. Определители 2-го и 3-го порядка

Пример
x2 1 1 1
1 1 1
1 1
3 2 2 5 0 0 5
4 3
5 4 3
5 4 3
5 3 4 5