Similar presentations:
5_Вариационные_методы_на_примере_задач_расчета_пластинок (6)
1. Вариационные методы на примере задач расчета пластинок
2.
Функция y=f(x)Функционал
b
y
F f x dx
δy
a
dy
dx
dy – приращение
функции y=f(x)
x
δy – вариация
функции y=f(x)
Функция превращает
множество чисел x в
множество чисел y
Функционал превращает
функции в числа
f x вариация функции f x
F вариация функционала F
b
F f x dx
a
Оператор превращает
функции в другие функции
3.
Вариационные принципы строительной механикиПолной потенциальной энергией упругой системы Э
называется работа, которую совершают внутренние и
внешние силы при переходе системы из
деформированного в недеформированное (начальное)
состояние
Э U A
U потенциальная энергия внутренних сил
А потенциальная энергия внешних сил
Принцип возможных перемещений. Если система
находится в состоянии равновесия, то сумма работ
всех внешних и внутренних сил на любом возможном
бесконечно малом перемещении равна нулю.
4.
Принцип Лагранжа. Из всех возможных перемещенийупругого тела действительные перемещения
соответствуют минимуму полной потенциальной
энергии.
Принцип Лежена-Дирихле.
•при устойчивом равновесии упругой системы полная
потенциальная энергия имеет минимум
Э min, Э 0, Э 0
2
•при неустойчивом равновесии упругой системы полная
потенциальная энергия имеет максимум
Э max, Э 0, Э 0
2
•при безразличном типе равновесия полная потенциальная
энергия постоянна
2
Э
const
,
Э
0,
Э 0
5.
Потенциальная энергия упругих пластинок1
U 0 x x y y xy xy ,
2
2
2
2
2
2
Ez
w w w
2 2
U0
w 2 1 2
,
2
2
2 1
x y x y
a b
A q x, y w dxdy
U U 0 dV ,
0 0
V
2
2
2
2
D 2 2
w w w
U w 2 1 2
dxdy
2
2 0 0
x y x y
a b
2
2
2
2
D 2 2
w w w
Э w 2 1 2
dxdy
2
2 0 0
x x x y
a b
a b
q x, y w dxdy
0 0
6.
Частные случаиДля пластинок с полностью защемленным контуром,
а также для пластинок с полностью шарнирно
(свободно) опертыми прямолинейными краями
2 w 2 w 2 w 2
0 0 x 2 y 2 x y dxdy 0,
a b
a b
a b
D
Э 2 w dxdy w q x, y dxdy
2 00
0 0
2
7.
Вариационный метод Ритца-ТимошенкоПрогиб пластинки ищем в виде разложения
n N
w x, y A1 1 x, y A2 2 x, y ... An n x, y An n x, y
n 1
x, y
j
N
j 1
система аппроксимирующих функций.
А1 , А2 ,..., Аn неизвестные постоянные числа.
Система аппроксимирующих функций должна быть полной.
Аппроксимирующие функции должны быть линейно независимыми.
Каждая из j x, y должна удовлетворять заданным
граничным условиям на контуре пластинки.
8.
Полная энергия есть функция обобщенных координатЭ Э А12 , А22 ,..., АN2 ,
Aj обобщенные координаты.
Э
Э
Э
Э
Э
А1
А2
А3 ...
Аn 0,
А1
А2
А3
Аn
Э
Э
Э
Э
0,
0,
0, ... ,
0.
А1
А2
А3
АN
x
q(x,y)
y
a
b
9.
22
a b
2
2
2
Э D
2
n
n
n
A
An
An n 2 1 An
dxdy
2 n
2
Aj 2 0 0 Aj
x y
x n
y
n
n
n
a b
q
0 0
An n dxdy
Aj n
2
2
2 j
2 j
2 n j
2 n
2 n
D An n j 1 2 An
2 An
2
An
2
2
x y n
x y
x
x n
y
n
y n
0 0
a b
a b
2 j 2 n 2 j 2 n
2 j 2 n
2
q j dxdy D An j n 1 2
2
2
dxdy
2
2
x y x y
x y
0 0
0 0
n
y x
a b
a b
q j dxdy 0
0 0
2
2
2
a b
2
2
2
1
j
j
j
n An j 2 n 1 y 2 x 2n x 2 y 2n 2 x y x yn dxdy D q j dxdy
0 0
0 0
a b
10.
22
2
2
2
2
n
j
j
j
2
n
n
jn j n 1 2
2
2
dxdy,
2
2
x y x y
x y
0 0
y x
a b
a b
1
j q j dxdy,
D00
A
jn
n
n
j
n 1, 2,..., N
j
1,
2,...,
N
Каноническая система уравнений метода Ритца-Тимошенко
11 12
21 22
...
...
N1 N 2
... 1N A1 1
... 2 N A2 2
... ... ... ...
... NN AN N
11. Вариационный метод Бубнова-Галеркина
Прогиб пластинки ищем в виде разложенияn N
w x, y A1 1 x, y A2 2 x, y ... An n x, y An n x, y
n 1
x, y
j
N
j 1
система аппроксимирующих функций.
А1 , А2 ,..., Аn неизвестные постоянные числа.
Система аппроксимирующих функций должна быть полной.
Аппроксимирующие функции должны быть линейно независимыми.
Каждая из j x, y должна удовлетворять заданным
граничным условиям на контуре пластинки.
12.
В основе метода лежит принцип Лагранжав форме возможных работ
4
D w q, D An n q j dxdy 0,
n
0 0
a b
4
a b
a b
1
n An j n dxdy D q x, y j dxdy,
0 0
0 0
4
a b
a b
1
jn j n dxdy, j q x, y j dxdy,
D00
0 0
4
n 1, 2,..., N
n jn An j , j 1, 2,..., N
13.
Каноническая система уравненийметода Бубнова-Галеркина
11 12
21 22
...
...
N1 N 2
... 1N A1 1
... 2 N A2 2
... ... ... ...
... NN AN N
11 A1 12 A2 13 A3 ... 1N AN 1
21 A1 22 A2 23 A3 ... 2 N AN 2
31 A1 32 A2 33 A3 ... 3 N AN 3
.............................................................
N 1 A1 N 2 A2 N 3 A3 ... NN AN N
14.
Система функций 1 x , 2 x ,..., N x на отрезке a, bобразует ортогональную систему , если при j n имеем
b
x x dx 0
j
n
a
x, y D 4 An n x, y q x, y 0
n
4
0 0 x, y j x, y dxdy 0 0 j D n An n q dxdy 0,
a b
a b
a b
a b
1
4
n An j n dxdy D j q x, y dxdy
0 0
0 0
j x, y X j x Y j y
a b
q x, y q x q y
a
b
X x Y y dxdy X x dx Y y dy
j
0 0
j
j
0
j
0
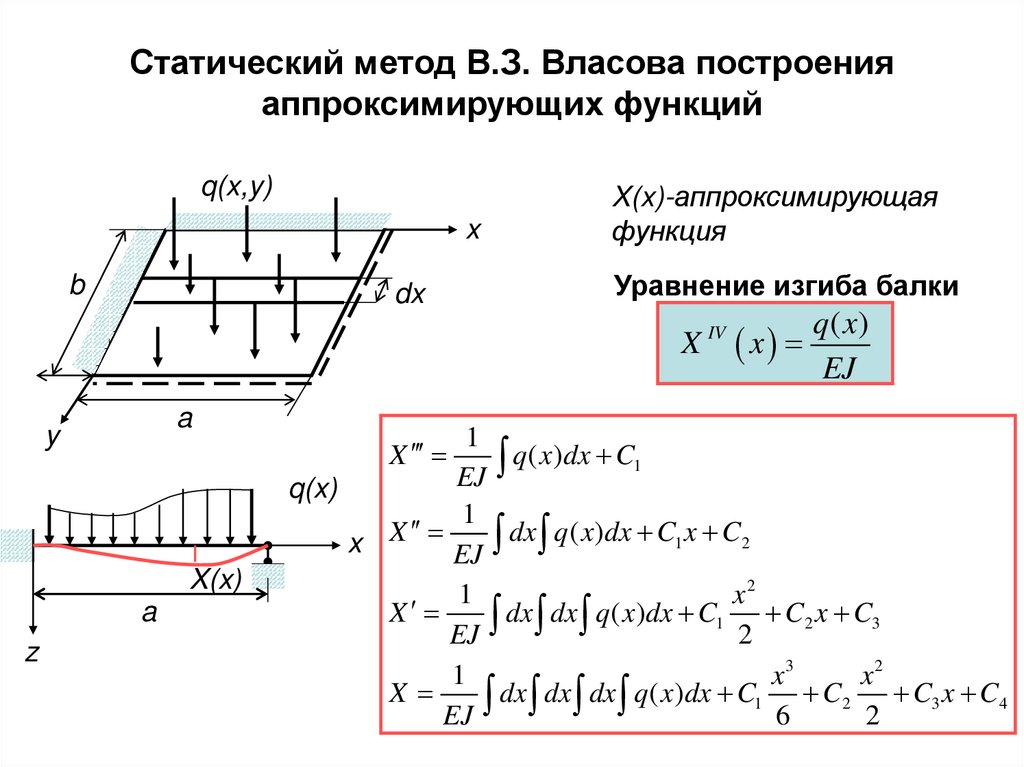
15.
Статический метод В.З. Власова построенияаппроксимирующих функций
q(x,y)
x
b
dx
X(x)-аппроксимирующая
функция
Уравнение изгиба балки
X
a
y
a
z
q( x)
x
EJ
1
q( x)dx C1
EJ
q(x)
1
x X EJ dx q ( x)dx C1 x C2
1
x2
X
dx dx q ( x)dx C1 C2 x C3
EJ
2
1
x3
x2
X
dx dx dx q ( x )dx C1 C2 C3 x C4
EJ
6
2
X
X(x)
IV
16.
1полагаем равной единице,
EJ
C1 , C2 , C3 , C4 находим из граничных условий балки
Граничные условия
при
x 0
X 0 0,
X 0 0
при
x a
X a 0,
X a 0
Введем обозначения
dx dx dx q x dx q x
dx dx q x dx q x
dx q x dx q x
q x dx q x
17.
Распишем граничные условияX 0 q 0 C4 0, C4 q 0
X 0 q 0 C3 0, C3 q 0
a3
a2
X a q a C1 C2
q 0 a q 0 0
6
2
X a q a C1a C2 0
a3
a2
C1 C2
q a q 0 a q 0
6
2
C1 , C2
C1a C2 q a
Аналогично строим функцию Y y
Аппроксимирующая функция для пластинки
x, y X x Y y
18.
Построение аппроксимирующих функций методомначальных параметров
P
q
x
ap
m
am
L
z
x am
x am
x
x
x
X x X 0 0 x M 0
Q0
q0
m
P
2 EJ y
6 EJ y
24 EJ y
2 EJ y
6 EJ y
2
3
4
2
3
X 0 , 0 , M 0 , Q0 , q0 прогиб , угол поворота, момент, поперечная сила,
интенсивность нагрузки в начале координат
Интеграл
Стилтьеса
0 Y y i Pi j m j dy i PYi yi j m jY y j
b
19. Вариационный метод Власова-Канторовича
Прогиб пластинки ищем в виде разложенияy аппроксимирующие функции
w x, y Wn x n y ,
N
n
n
1
Применяем принцип возможных работ к уравнению Софи Жермен
4
D w q x, y 0, D Wn x n y q x, y W j x j y dy 0
n
0
b
4
W j x j y j y W j x ,
b
W j x D 4 Wn x n y q x, y j y dy 0
0
n
b
W j x 0 следовательно D 4 Wn x n y q x, y j y dy 0
0
n
20.
bb
1
n Wn x n y j y dy D j y q x, y dy
0
0
4
4
4
4
4 4 2 2 2 4
x
x y y
b
b
1
IV
n W n 2Wn n Wn n j dy D j q x, y dy
0
0
IV
n
b
b
b
IV b
1
IV
W
dy
2
W
dy
W
j q x, y dy
n n j n
n j n
n j n dy
0
0
0
D0
b
b
b
0
0
0
a jn j n dy, b jn 2 j n dy, c jn j nIV dy
b
1
q x j q x, y dy
D0
21.
n 1, 2,..., Nn a jnW b jnWn c jnWn q j x j 1, 2,..., N
В первом приближении имеем
обыкновенное дифференциальное уравнение
IV
n
a11W1IV b11W1 c11W1 q1 x
Характеристическое уравнение
a11 4 b11 2 c11 0
если 1,2,3,4 k ri, то будем иметь решение
однородного уравнения в виде
W1,0 x C1sh kx sin rx C2 sh kx cos rx
C3ch kx sin rx C3ch kx cos rx
22.
Общее решение неоднородного уравнения имеет видW x C1sh kx sin rx C2 sh kx cos rx
C3 x sh kx sin rx C4 x sh kx cos rx W * x
Частное решение неоднородного уравнения W * x
ищем в виде правой части неоднородного уравнения
или методом вариации произвольных постоянных.
Произвольные постоянные С1 , С2 , С3 , С4 определяем
из граничных условий на краях пластинки
x 0, x a
23.
Смягчение граничных условийНа свободном крае пластинки x a вместо требования
M x a, y D X a Y y X a Y y 0, Qx* a, y 0
будем требовать равенство нулю суммарной работы изгибающих
моментов и перерезывающих сил Кирхгофа на соответствующих
перемещениях
w
M
0 x x dy D 0 X Y XY X Ydy 0
b
b
b
DX a X Y XY Ydy 0
b
b
Q wdy D X Y 2 X Y XYdy 0
*
x
0
0
b
DX a X Y 2 X Y Ydy 0
0
0
b
b
0
o
X a Y 2 dy X a YY dy 0
b
b
обозначим : Y dy, YY dy
2
0
X a X a 0
o
b
b
X a Y dy 2 X a YY dy 0
2
0
o
X a X a 0
24.
Метод вариационных итерацийПервая итерация
w x, y X x Y y , Y y аппроксимирующая функция
X x решение уравнения a1 X IV b1 X c1 X q x
b
b
b
0
0
0
a1 Y 2 dy, b1 2 YY dy, c1 YY IV dy
Вторая итерация
w x, y X x Y y ,
X x аппроксимирующая функция
Y y решение уравнения a2Y IV b2Y c2Y q y
a
a
a
0
0
0
a2 X 2 dx, b2 2 XX dx, c2 XX IV dx








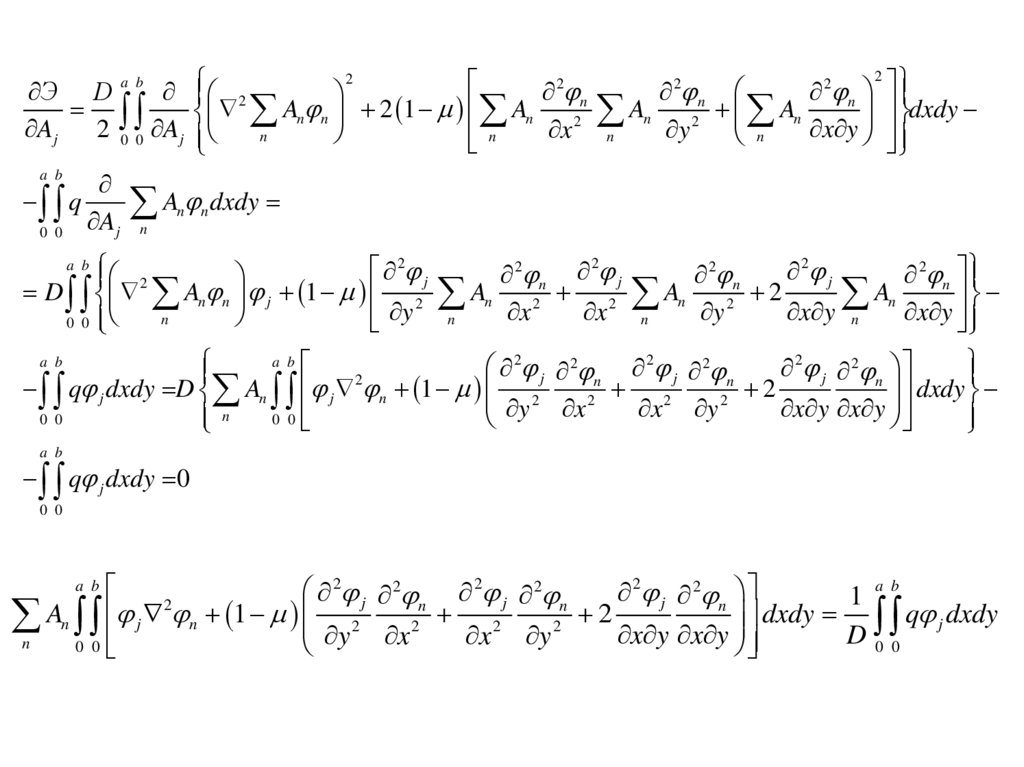




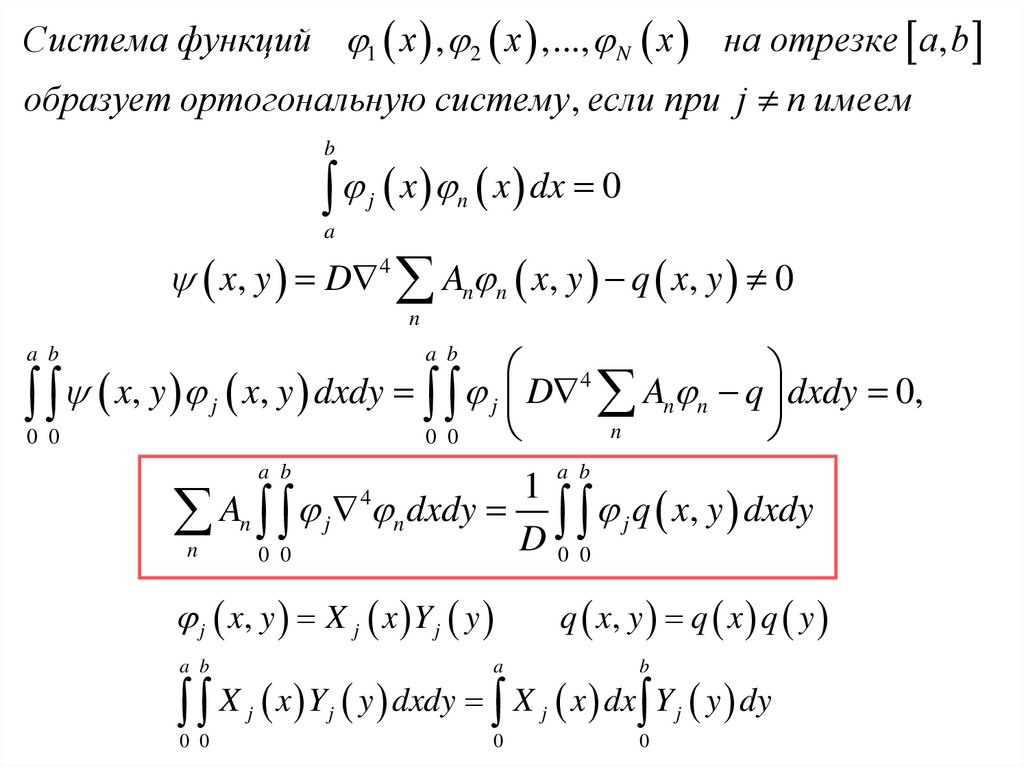




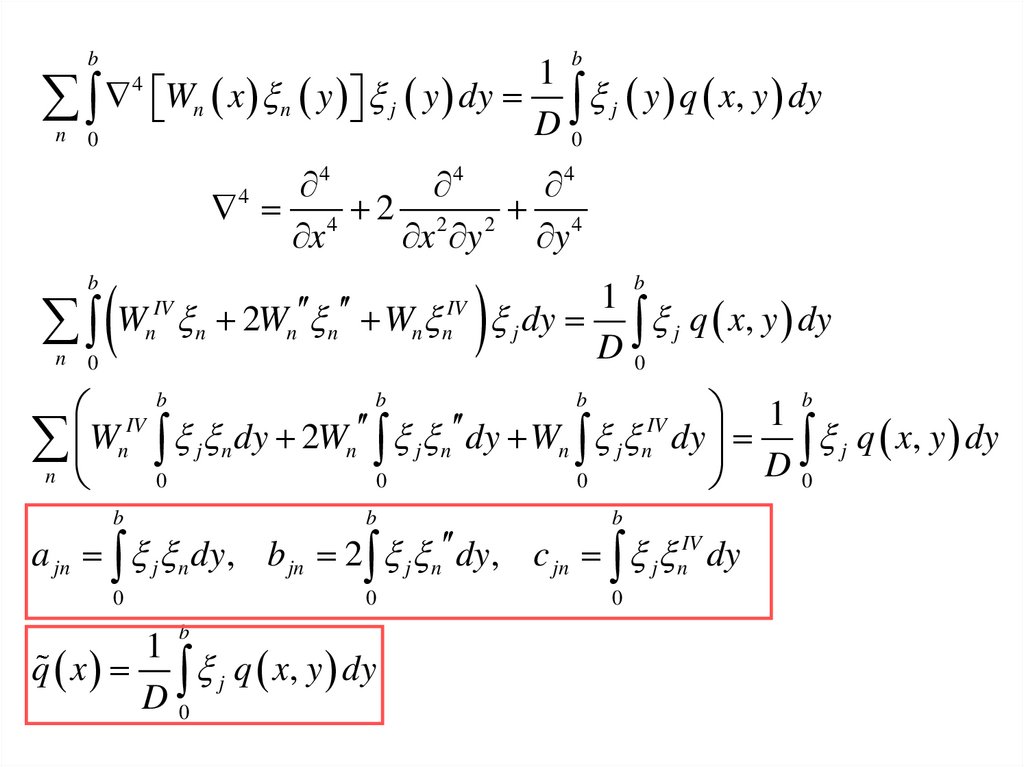




 mathematics
mathematics








