Перспектива точки и прямой

1.

Санкт-Петербургский государственный
архитектурно-строительный университет
кафедра начертательной геометрии и инженерной
графики
Начертательная геометрия
h
S
к
°
P А'
°
А
°
°
ok
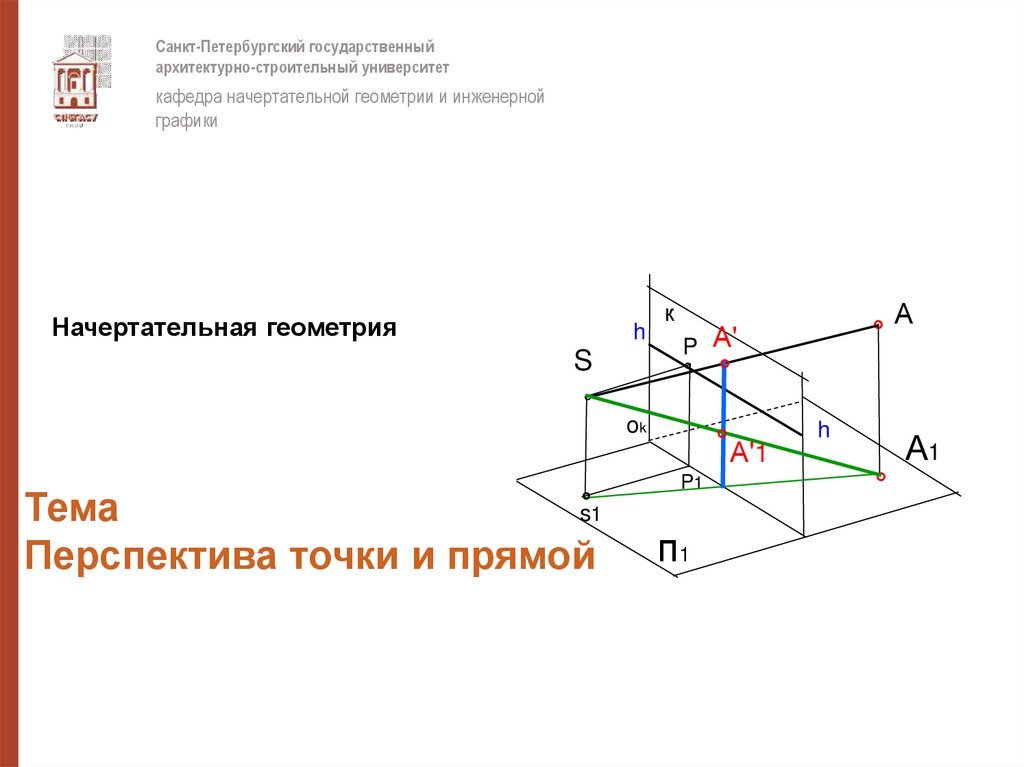
Тема
Перспектива точки и прямой
°
s1
° А'1
P1
п1
h
°
А1

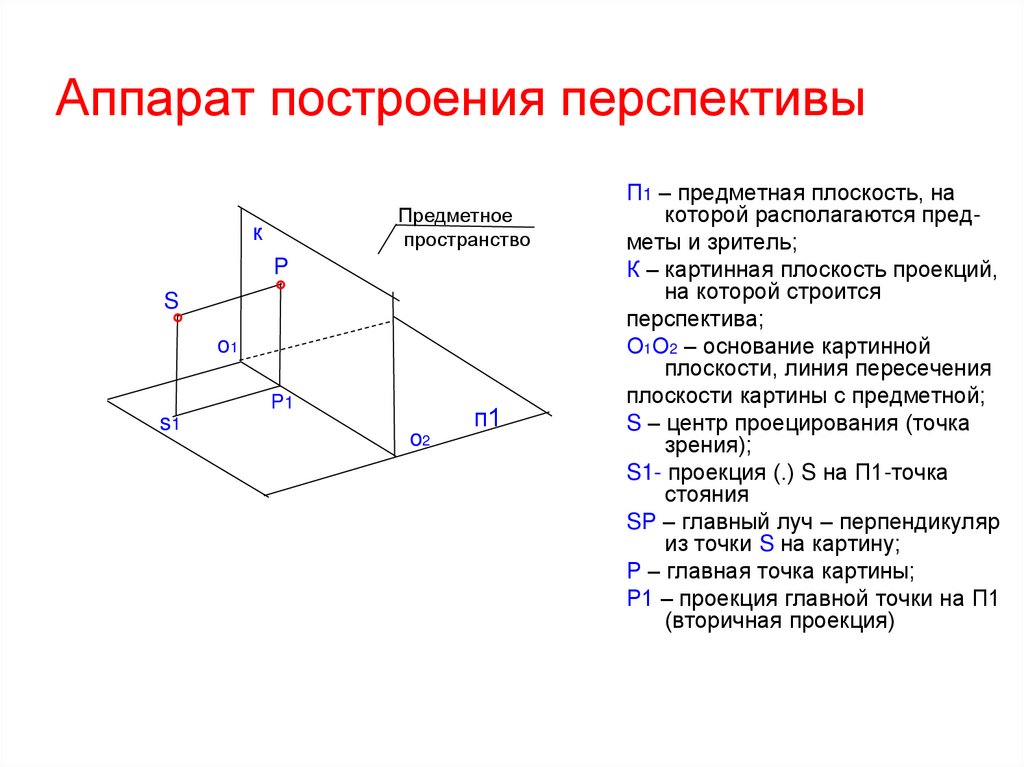
2. Аппарат построения перспективы

Предметное
пространство
к
P
°
S
°
o1
P1
s1
o2
п1
П1 – предметная плоскость, на
которой располагаются предметы и зритель;
К – картинная плоскость проекций,
на которой строится
перспектива;
О1О2 – основание картинной
плоскости, линия пересечения
плоскости картины с предметной;
S – центр проецирования (точка
зрения);
S1- проекция (.) S на П1-точка
стояния
SР – главный луч – перпендикуляр
из точки S на картину;
Р – главная точка картины;
Р1 – проекция главной точки на П1
(вторичная проекция)

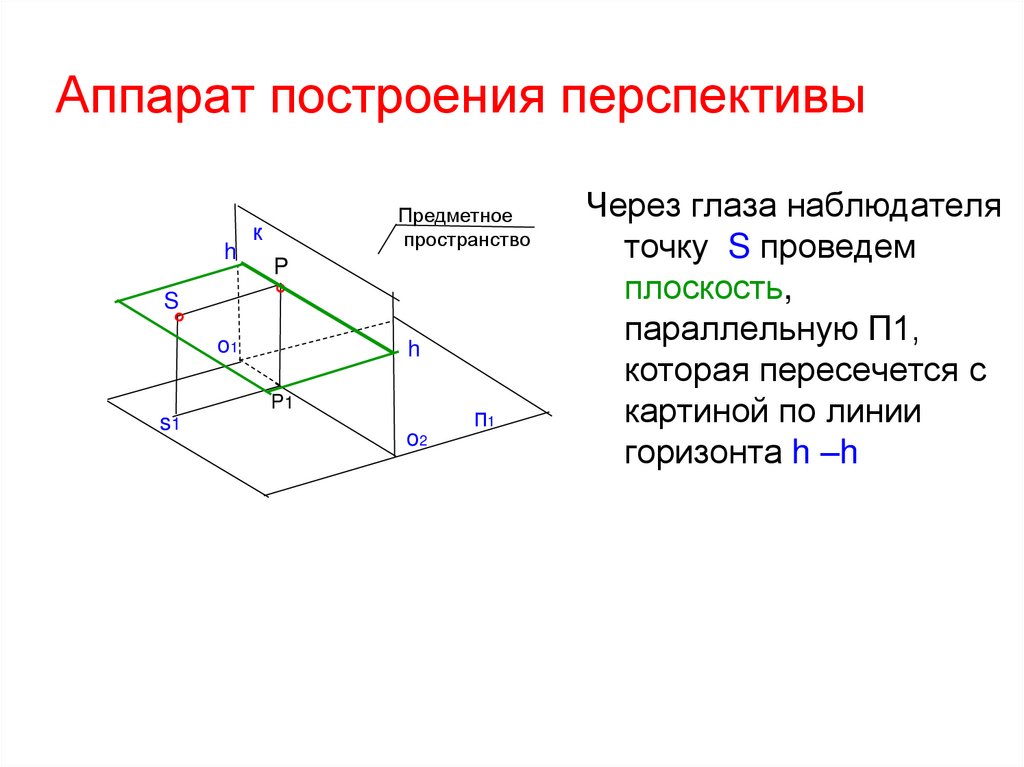
3. Аппарат построения перспективы

h
к
P
°
S
°
Предметное
пространство
o1
h
P1
s1
o2
п1
Через глаза наблюдателя
точку S проведем
плоскость,
параллельную П1,
которая пересечется с
картиной по линии
горизонта h –h

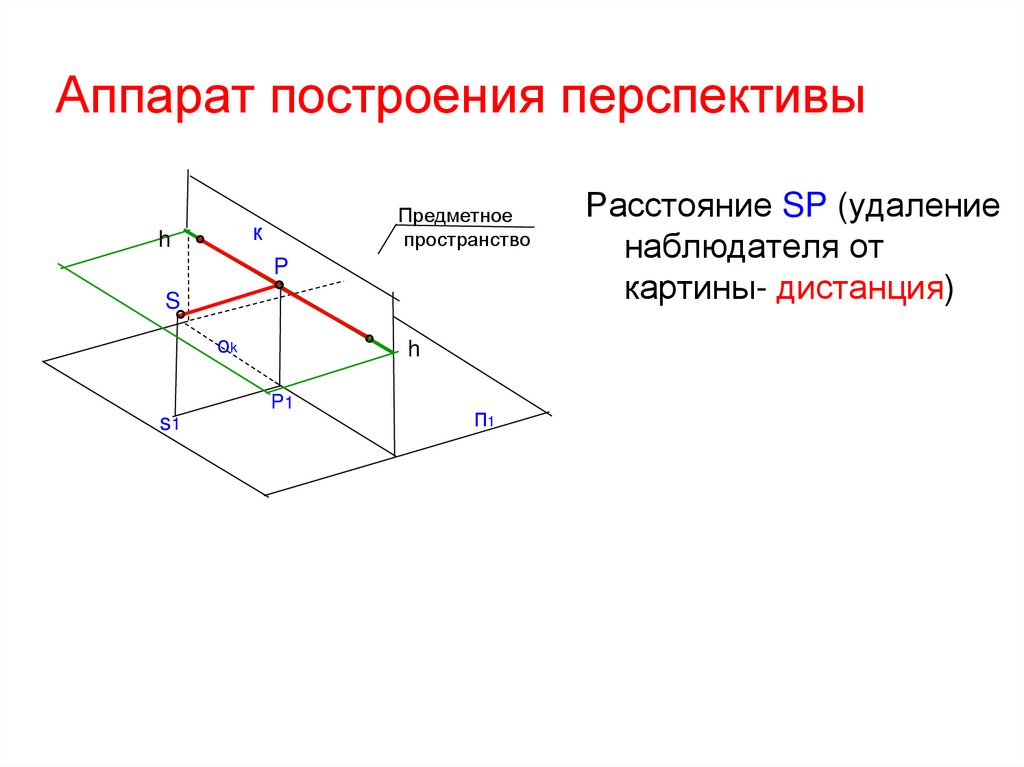
4. Аппарат построения перспективы

к
°
h
P
°
S
°
Предметное
пространство
°
ok
P1
s1
h
п1
Расстояние SP (удаление
наблюдателя от
картины- дистанция)

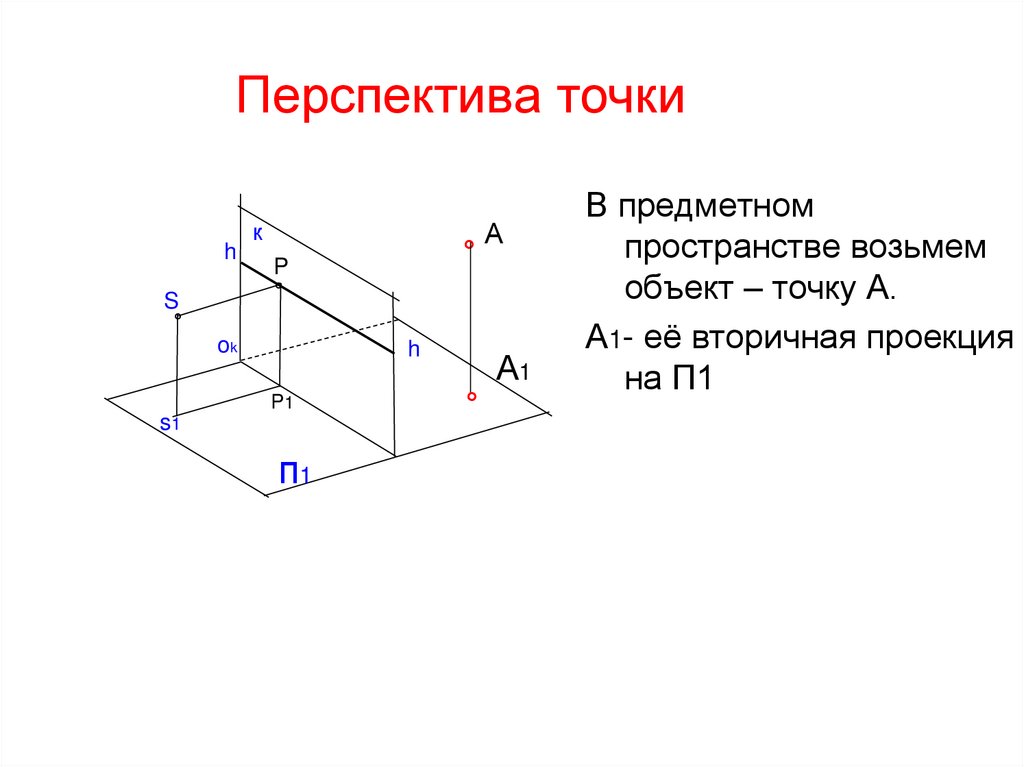
5. Перспектива точки

h
к
°
P
А
°
S
°
ok
h
P1
s1
п1
°
А1
В предметном
пространстве возьмем
объект – точку А.
А1- её вторичная проекция
на П1

6. Перспектива точки

h
°
P
А
°
S
°
к
ok
h
P1
s1
п1
°
А1
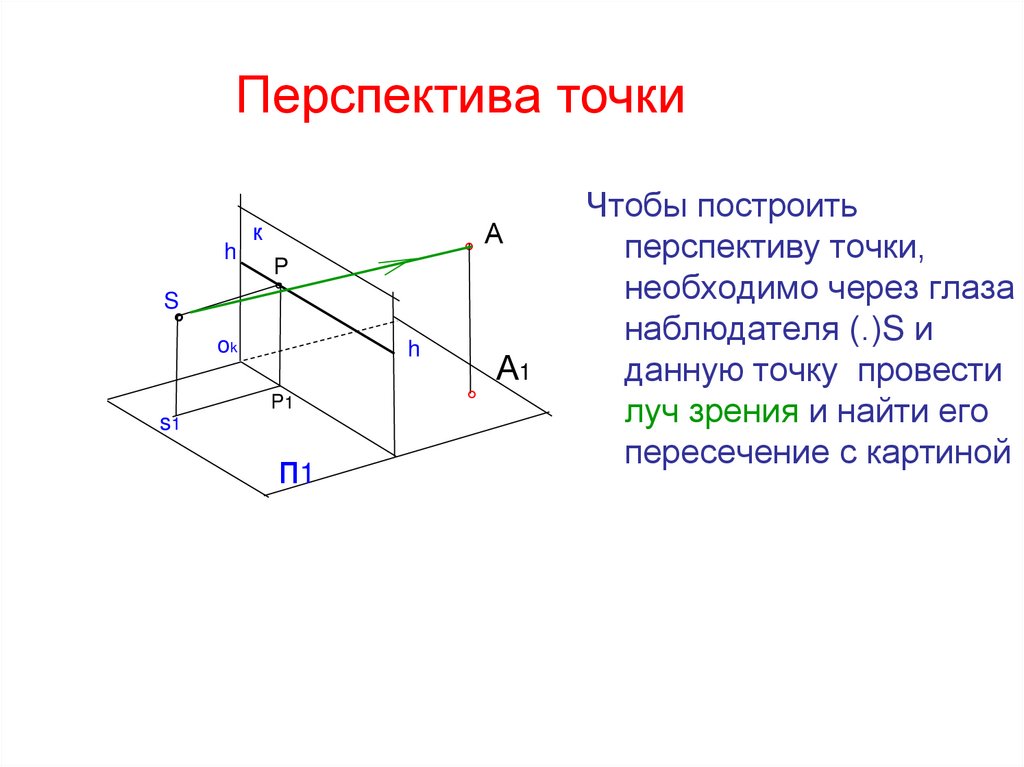
Чтобы построить
перспективу точки,
необходимо через глаза
наблюдателя (.)S и
данную точку провести
луч зрения и найти его
пересечение с картиной

7. Перспектива точки

h
к
P А'
°
S
°
А
°
°
ok
s°1
h
P1
п1
°
А1
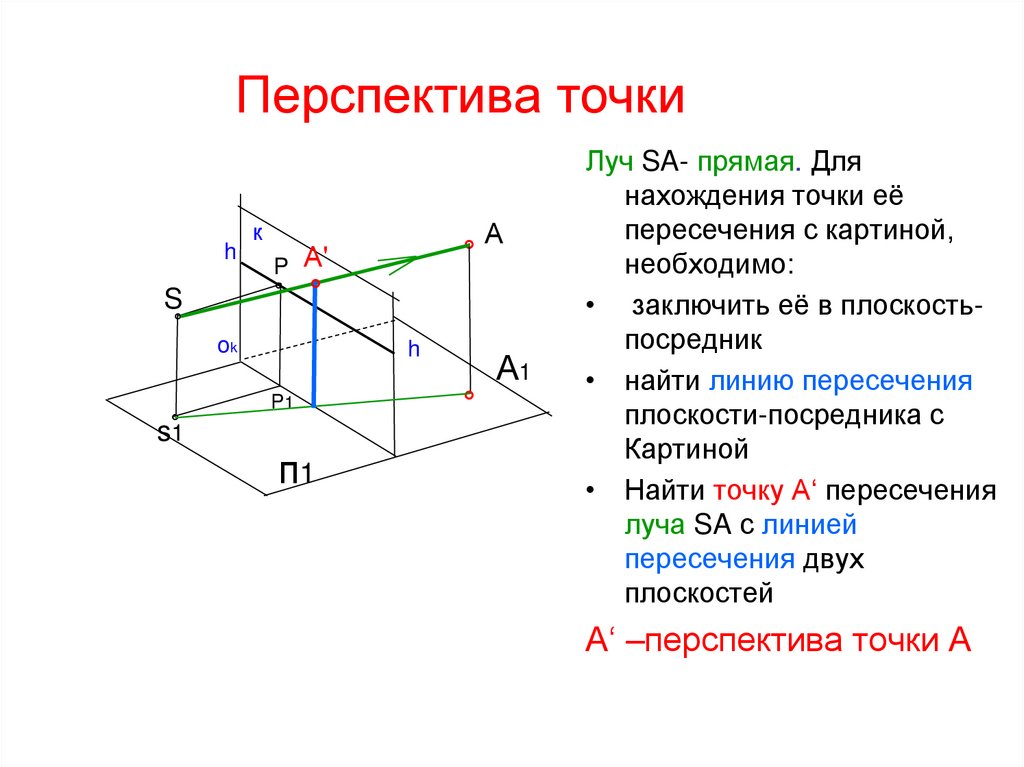
Луч SA- прямая. Для
нахождения точки её
пересечения с картиной,
необходимо:
• заключить её в плоскостьпосредник
• найти линию пересечения
плоскости-посредника с
Картиной
• Найти точку А‘ пересечения
луча SA с линией
пересечения двух
плоскостей
А‘ –перспектива точки А

8. Перспектива точки

h
к
S
°
P А'
°
А
°
°
ok
h
° А'1
°
P1
°
s1
п1
h
Р
°
А'
h
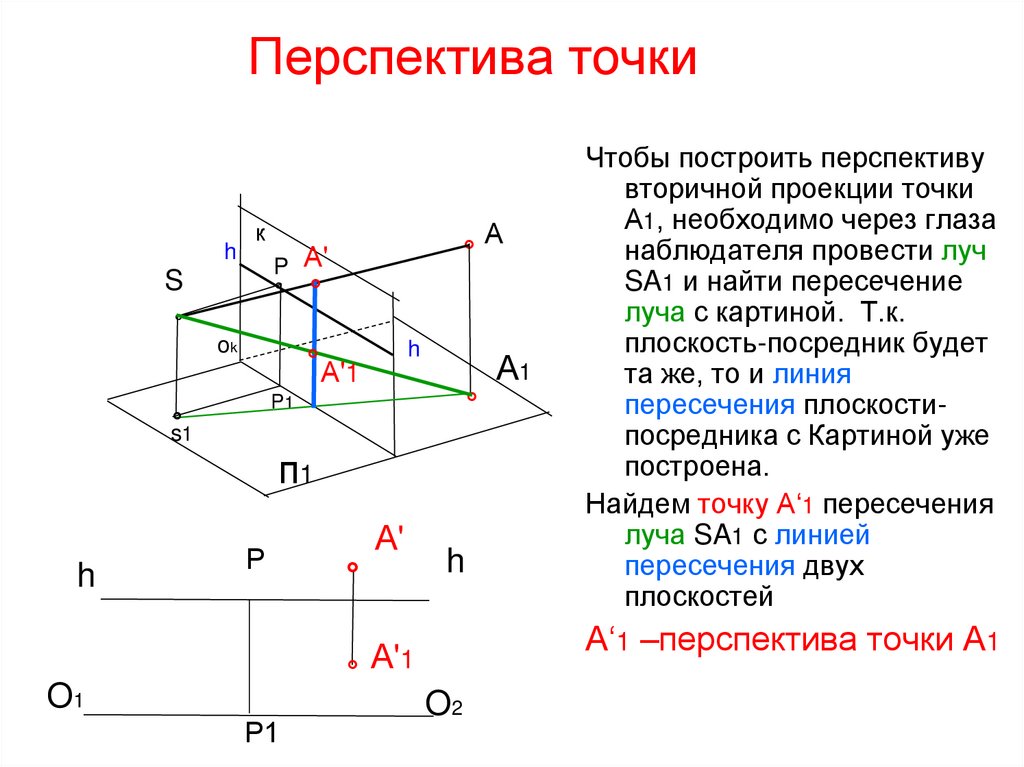
А‘1 –перспектива точки А1
° А'1
O1
Р1
А1
Чтобы построить перспективу
вторичной проекции точки
А1, необходимо через глаза
наблюдателя провести луч
SA1 и найти пересечение
луча с картиной. Т.к.
плоскость-посредник будет
та же, то и линия
пересечения плоскостипосредника с Картиной уже
построена.
Найдем точку А‘1 пересечения
луча SA1 с линией
пересечения двух
плоскостей
O2

9. Перспектива прямой

h
к
P
°
S
°
ok
s1°
h
P1
п1
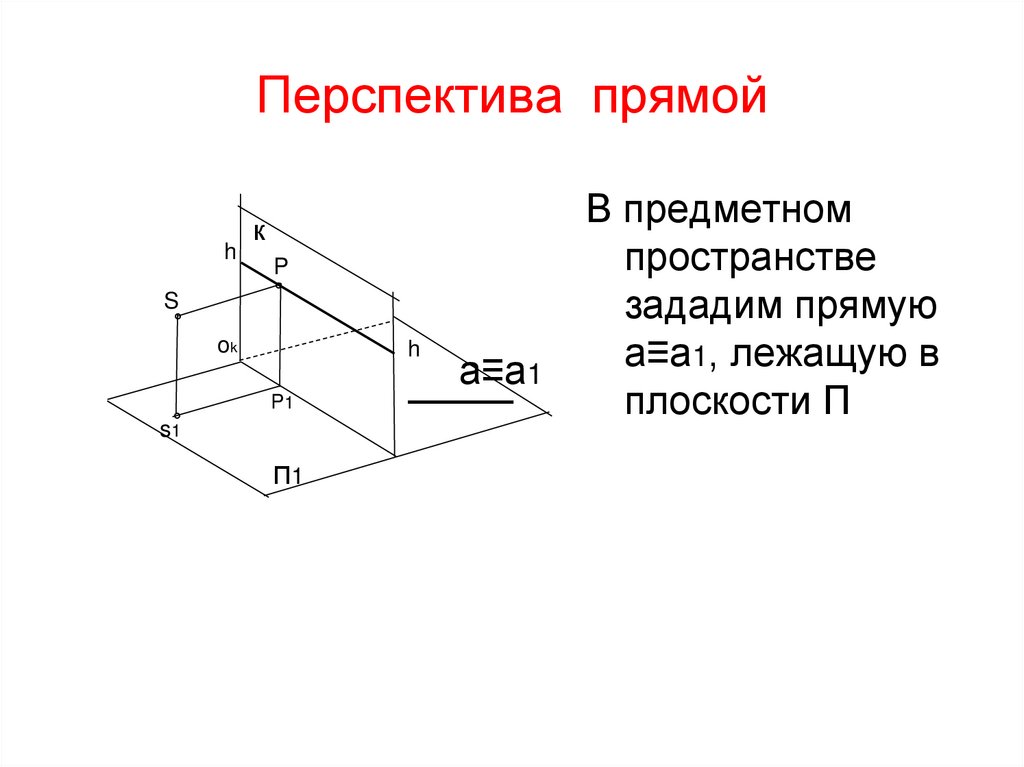
а≡а1
В предметном
пространстве
зададим прямую
а≡а1, лежащую в
плоскости П

10. Перспектива прямой

h
P
°
S
°
к
ok
h
P1
s1
°Ак
п1
а≡а1
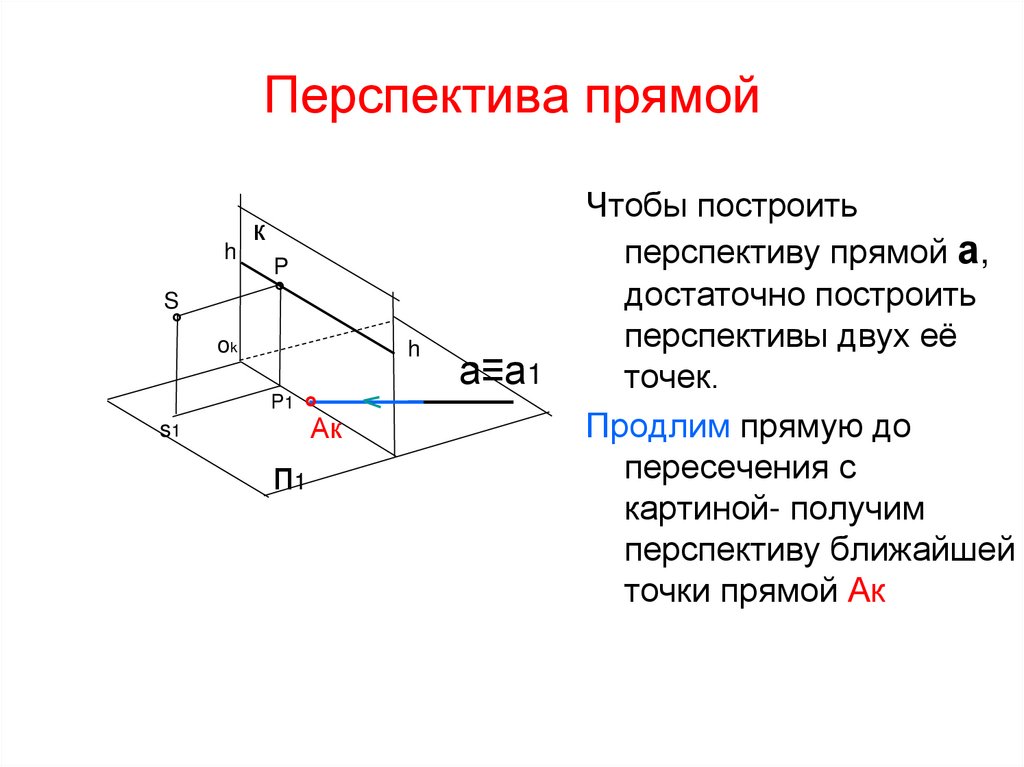
Чтобы построить
перспективу прямой а,
достаточно построить
перспективы двух её
точек.
Продлим прямую до
пересечения с
картиной- получим
перспективу ближайшей
точки прямой Ак

11. Перспектива прямой

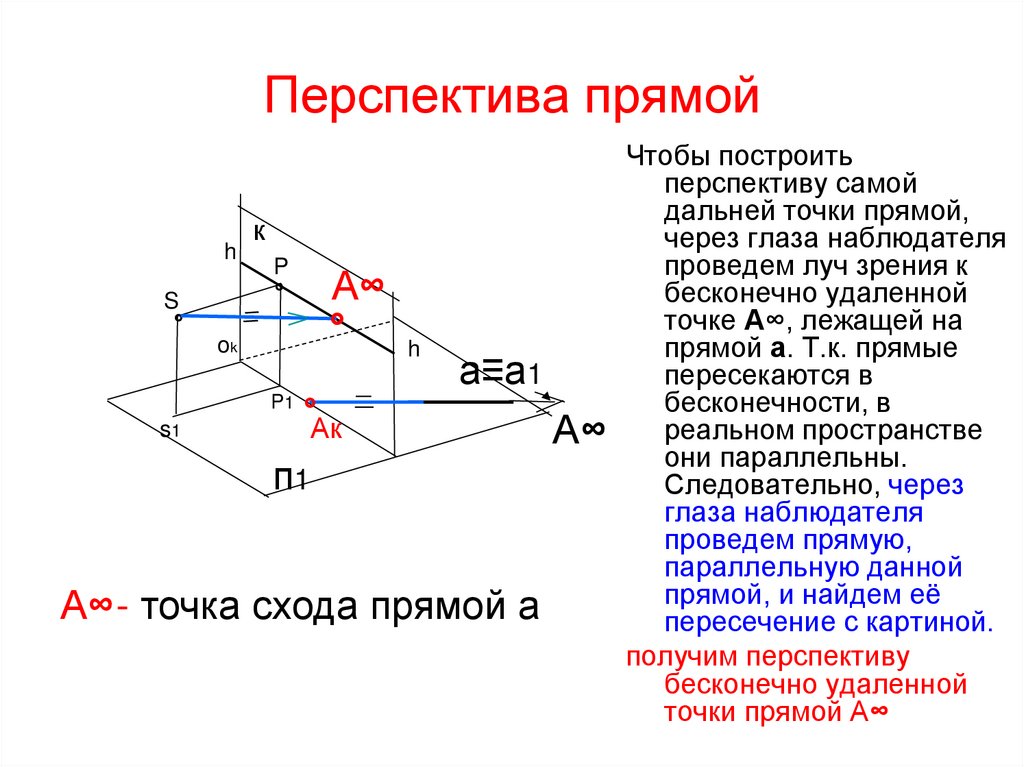
Чтобы построить
перспективу самой
дальней точки прямой,
к
через глаза наблюдателя
h
P
проведем луч зрения к
А∞
°
бесконечно удаленной
S
точке А∞, лежащей на
°
°
ok
h
прямой а. Т.к. прямые
а≡а1
пересекаются в
P1
бесконечности, в
°
s1
Ак
А∞ реальном пространстве
они параллельны.
п1
Следовательно, через
глаза наблюдателя
проведем прямую,
параллельную данной
прямой, и найдем её
А∞- точка схода прямой а
пересечение с картиной.
получим перспективу
бесконечно удаленной
точки прямой А∞

12. Перспектива прямой

h
к
P
А∞
°
h
а1'
а≡а1
°
S
°
ok
P1
s1
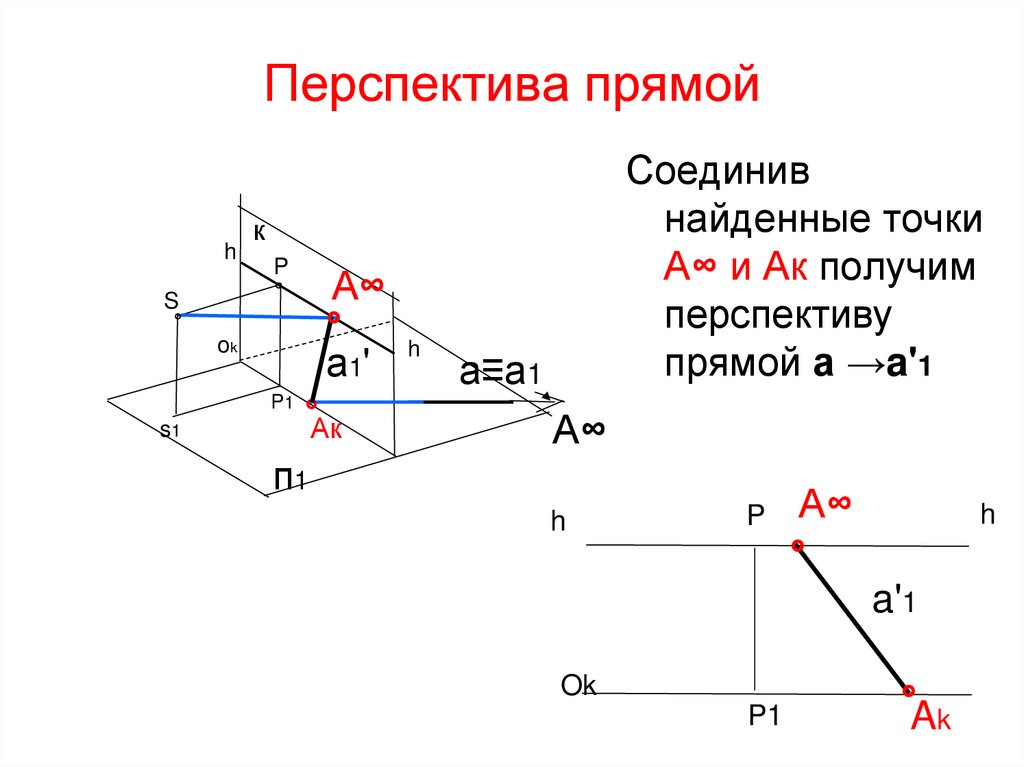
Соединив
найденные точки
А∞ и Ак получим
перспективу
прямой а →a'1
°Ак
А∞
п1
h
P
А∞
°
h
a'1
Ok
P1
°Ak

13. Перспектива параллельных прямых

h
к
P
А∞
°
S
°
°
ok
s1
а1'
P1 °
Ак
п1
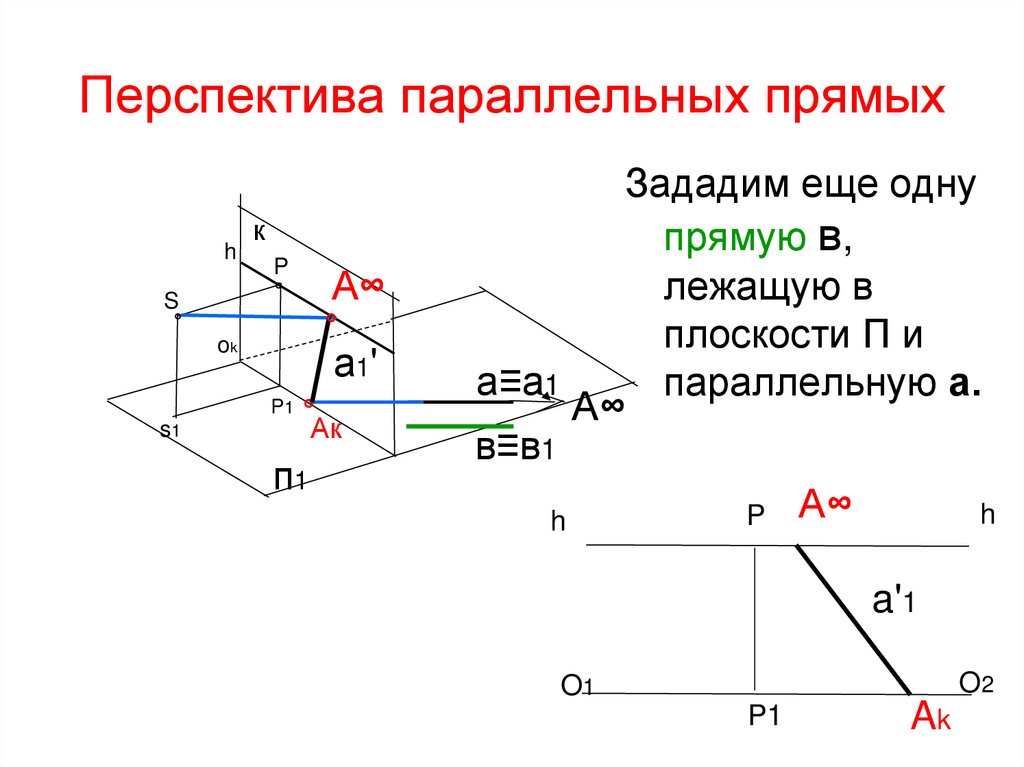
Зададим еще одну
прямую в,
лежащую в
плоскости П и
а≡а1
параллельную а.
А∞
в≡в1
h
P А∞
h
a'1
O2
O1
P1
Ak

14. Перспектива параллельных прямых

S
°
s1
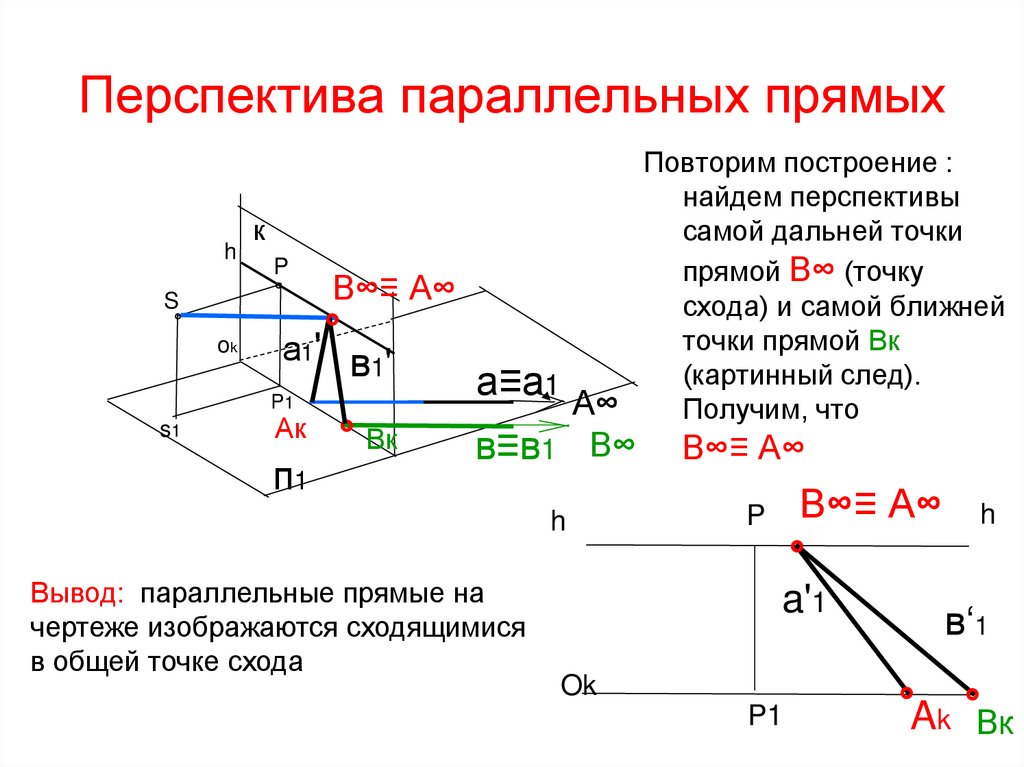
Повторим построение :
найдем перспективы
к
самой дальней точки
h
P
прямой В∞ (точку
°
В∞≡ А∞
схода) и самой ближней
°
точки прямой Вк
ok
а1' в1'
(картинный след).
а≡а
1
P1
А∞
Получим, что
Ак ° Вк
в≡в1 В∞ В∞≡ А∞
п1
h
Вывод: параллельные прямые на
чертеже изображаются сходящимися
в общей точке схода
P
В∞≡ А∞
°
a'1
Ok
P1
h
в‘1
°Ak °Вк

15. Перспектива параллельных прямых

S
°
s1
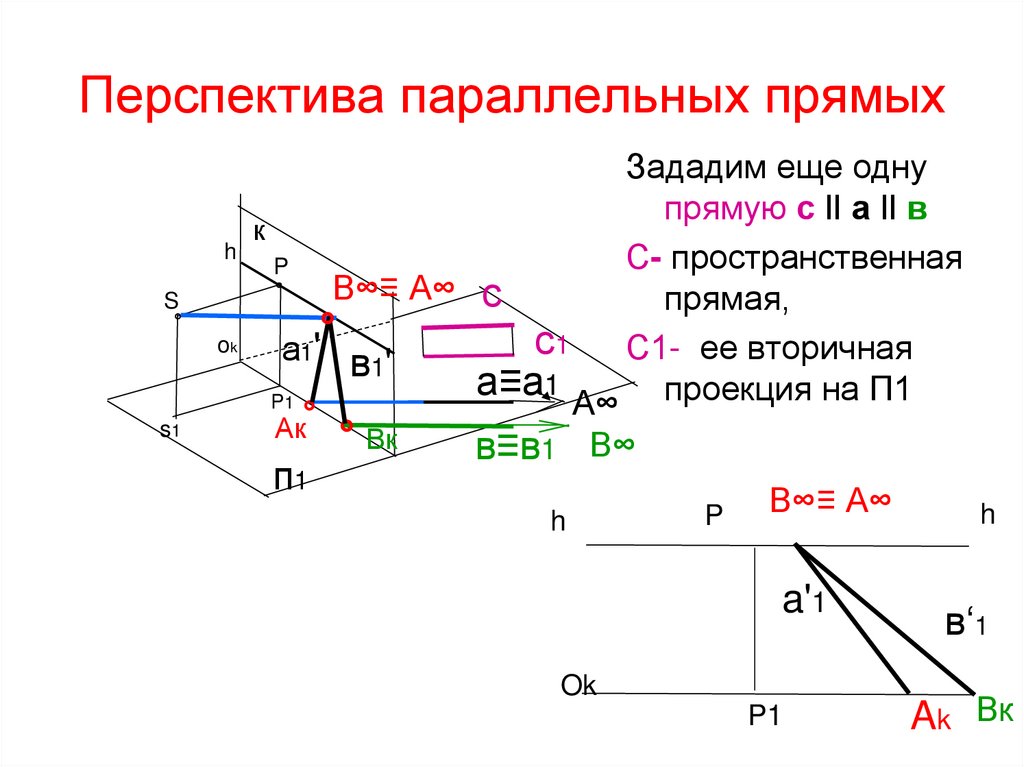
Зададим еще одну
прямую с ‖ а ‖ в
к
h
С- пространственная
P
°
В∞≡ А∞ с
прямая,
°
ok
с1 С1- ее вторичная
а1' в1'
а≡а1
проекция на П1
P1
А∞
Ак° ° Вк
в≡в1 В∞
п1
h
P
В∞≡ А∞
a'1
Ok
P1
h
в‘1
Ak Вк

16. Перспектива параллельных прямых

h
к
P
S
°
Ск ° В∞≡ А∞ ≡ С∞
°
а1'
°
ск
с
с1
а≡а1
в1'
P1
s1
Ак
п1
Вк
ok
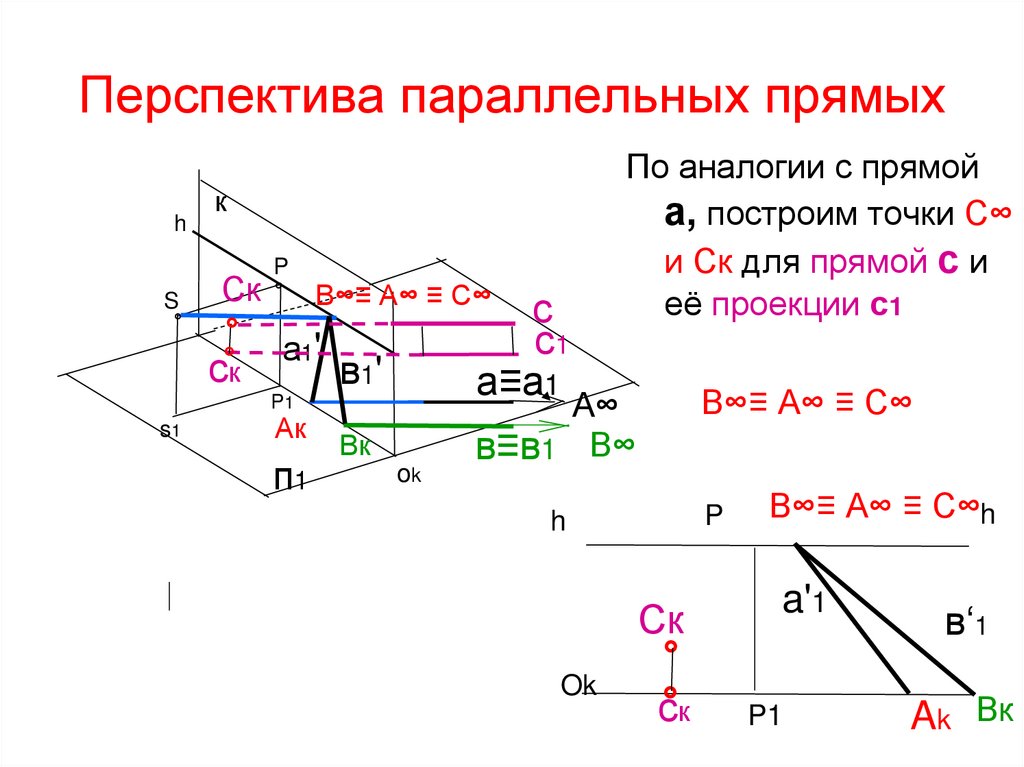
По аналогии с прямой
а, построим точки С∞
и Ск для прямой с и
её проекции с1
В∞≡ А∞ ≡ С∞
А∞
в≡в1 В∞
P
h
Ok
Ск
°
с°к
В∞≡ А∞ ≡ С∞h
a'1
P1
в‘1
Ak Вк

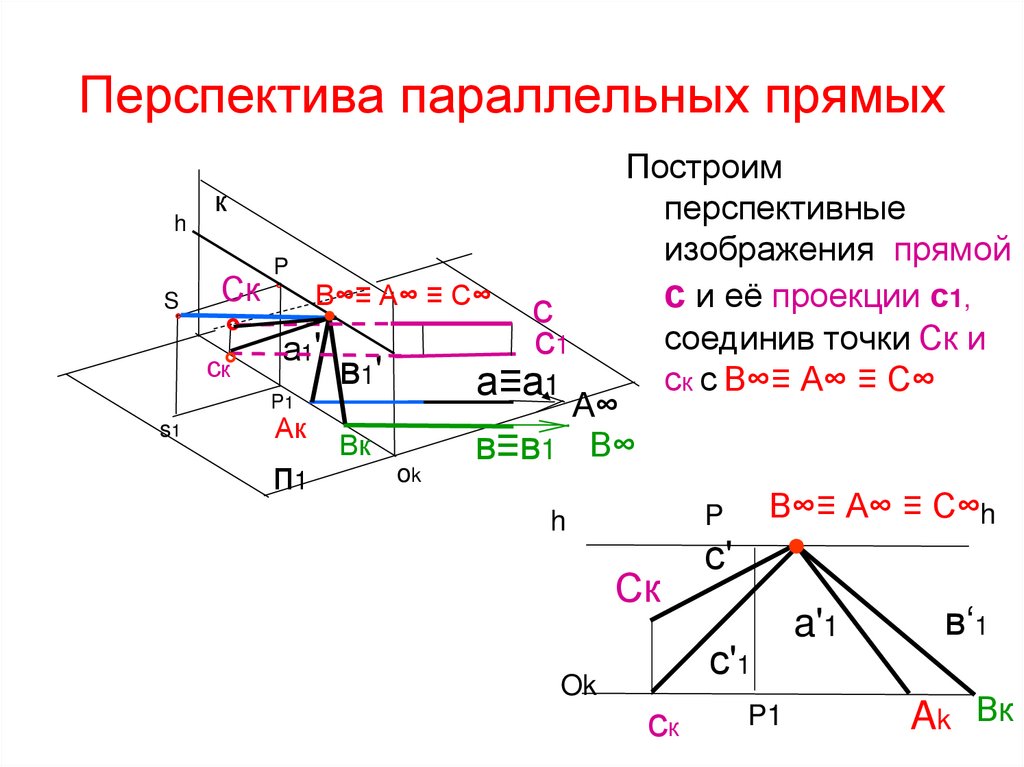
17. Перспектива параллельных прямых

h
к
P
S
°
Ск ° В∞≡ А∞ ≡ С∞
°
ск°
с
с1
а≡а1
а1'
в1'
P1
s1
Ак
п1
Вк
ok
Построим
перспективные
изображения прямой
с и её проекции с1,
соединив точки Ск и
ск с В∞≡ А∞ ≡ С∞
А∞
в≡в1 В∞
Ск
Ok
В∞≡ А∞ ≡ С∞h
P
h
с'
с'1
ск
P1
a'1
в‘1
Ak Вк

18. Параллельные прямые имеют общую точку схода. Точка схода- перспектива бесконечно удаленной точки прямой. Чтобы построить точку

схода
прямой, необходимо через глаза
наблюдателя провести прямую,
параллельную данной прямой и
найти ее пересечение с картиной

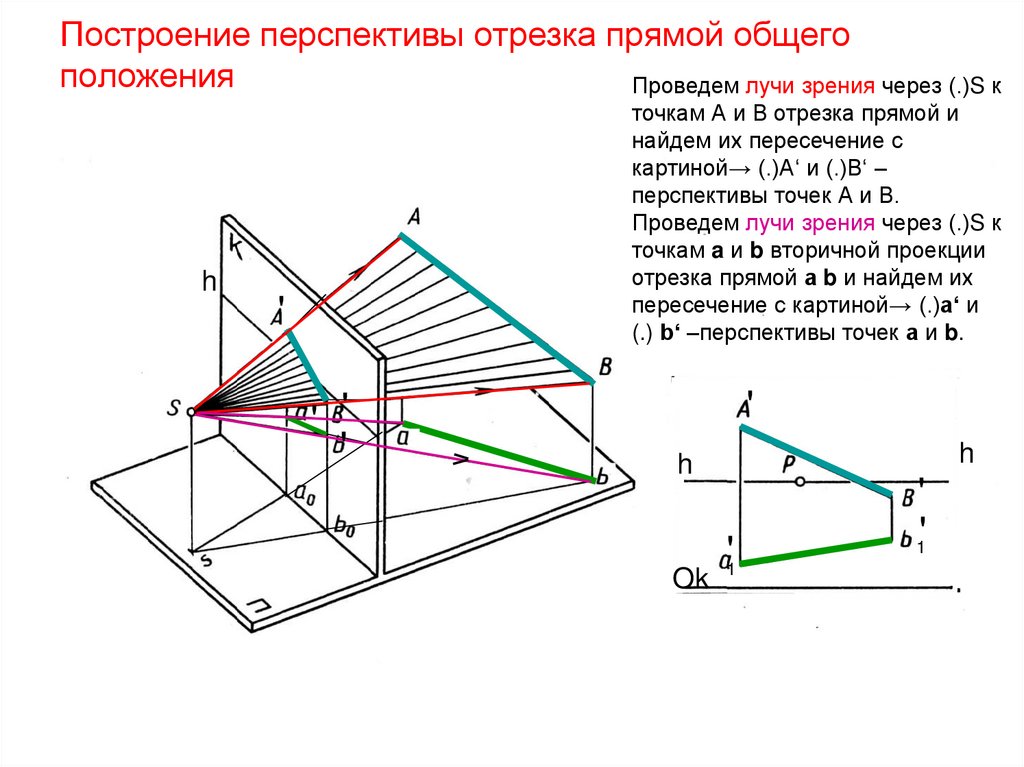
19. Построение перспективы отрезка прямой общего положения

Проведем лучи зрения через (.)S к
h
точкам А и В отрезка прямой и
найдем их пересечение с
картиной→ (.)А‘ и (.)В‘ –
перспективы точек А и В.
Проведем лучи зрения через (.)S к
точкам a и b вторичной проекции
отрезка прямой а b и найдем их
пересечение с картиной→ (.)а‘ и
(.) b‘ –перспективы точек а и b.
'
' '
'
'
h
h
Ok
'
1
'
'
1

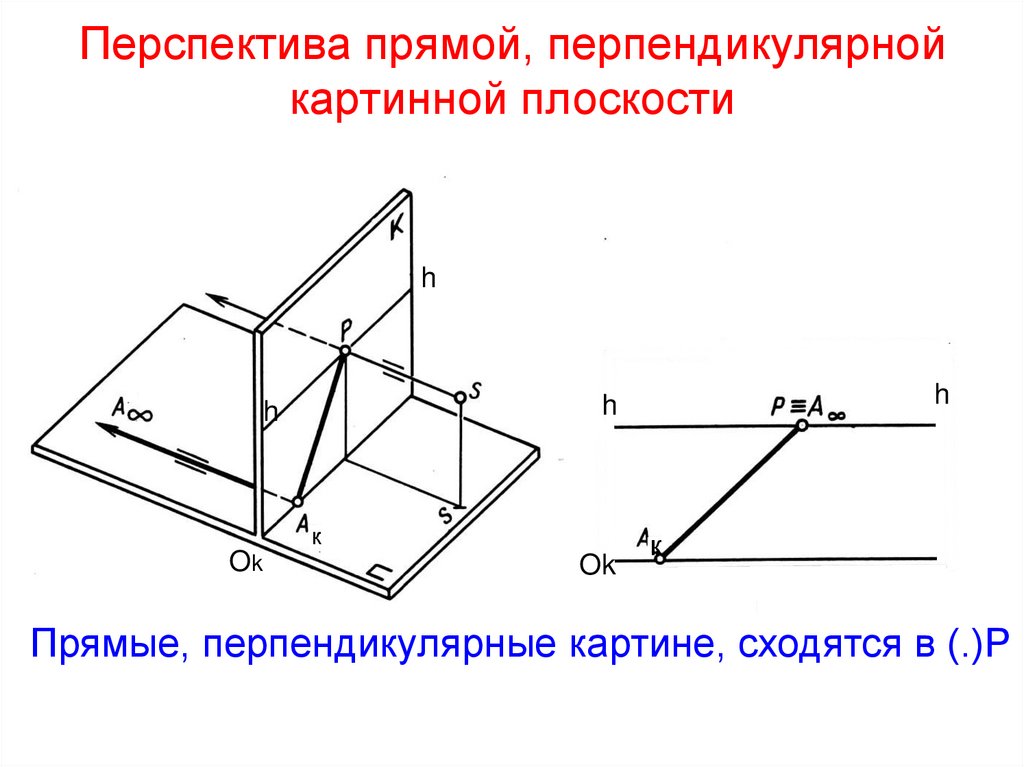
20. Перспектива прямой, перпендикулярной картинной плоскости

h
к
Ok
h
h
h
Ok
к
Прямые, перпендикулярные картине, сходятся в (.)Р

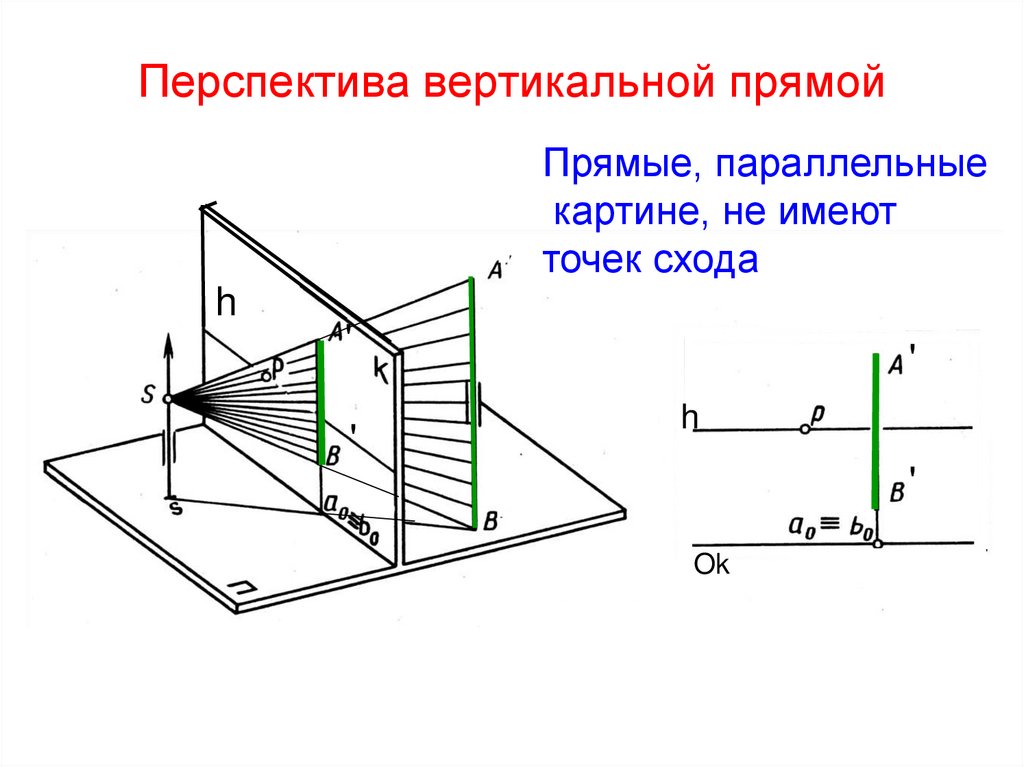
21. Перспектива вертикальной прямой

Прямые, параллельные
картине, не имеют
точек схода
h
'
'
'
h
'
Ok

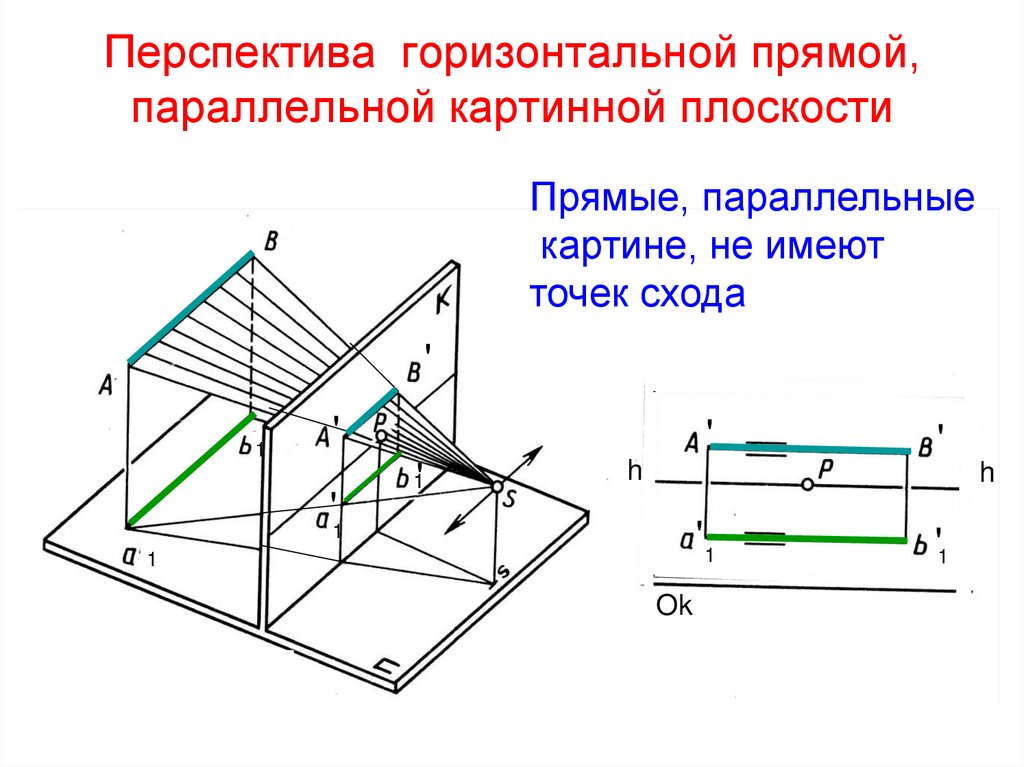
22. Перспектива горизонтальной прямой, параллельной картинной плоскости

Прямые, параллельные
картине, не имеют
точек схода
'
1
'
'1
'
'
1
h
'
h
'1
1
Ok
'1

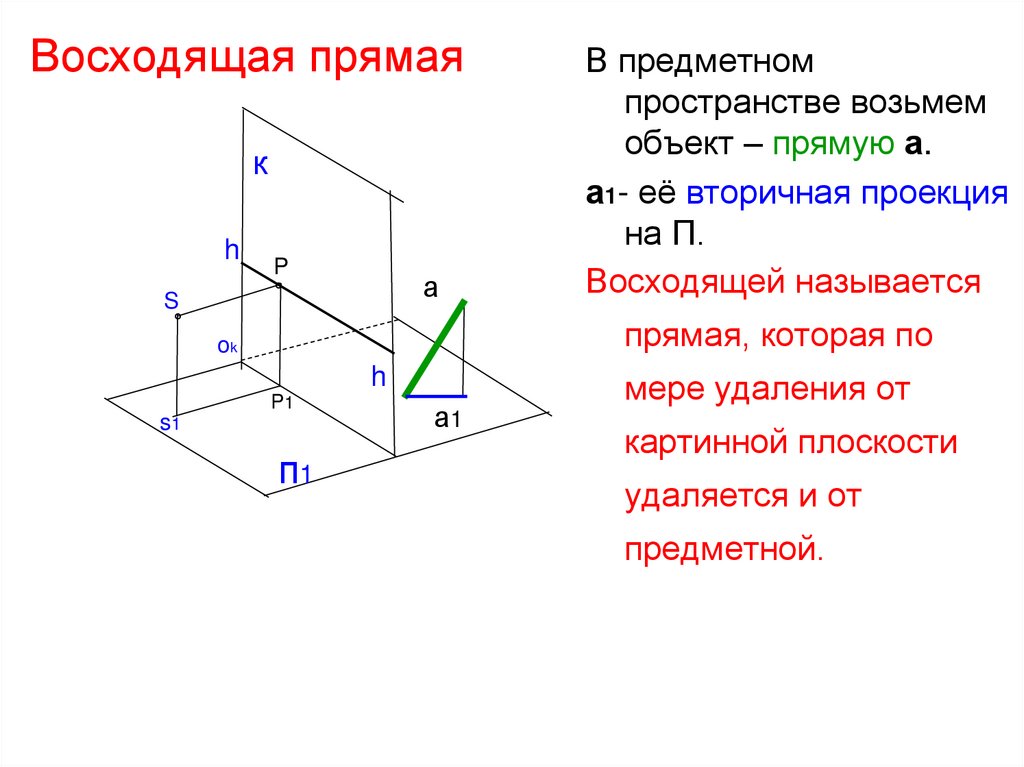
23. Восходящая прямая

к
h
P
а
°
S
°
В предметном
пространстве возьмем
объект – прямую а.
а1- её вторичная проекция
на П.
Восходящей называется
прямая, которая по
ok
h
P1
s1
п1
а1
мере удаления от
картинной плоскости
удаляется и от
предметной.

24.

А∞
к
°
h
P
°
S
°
ok
P1
s1
п1
°
а∞
а
h
а1
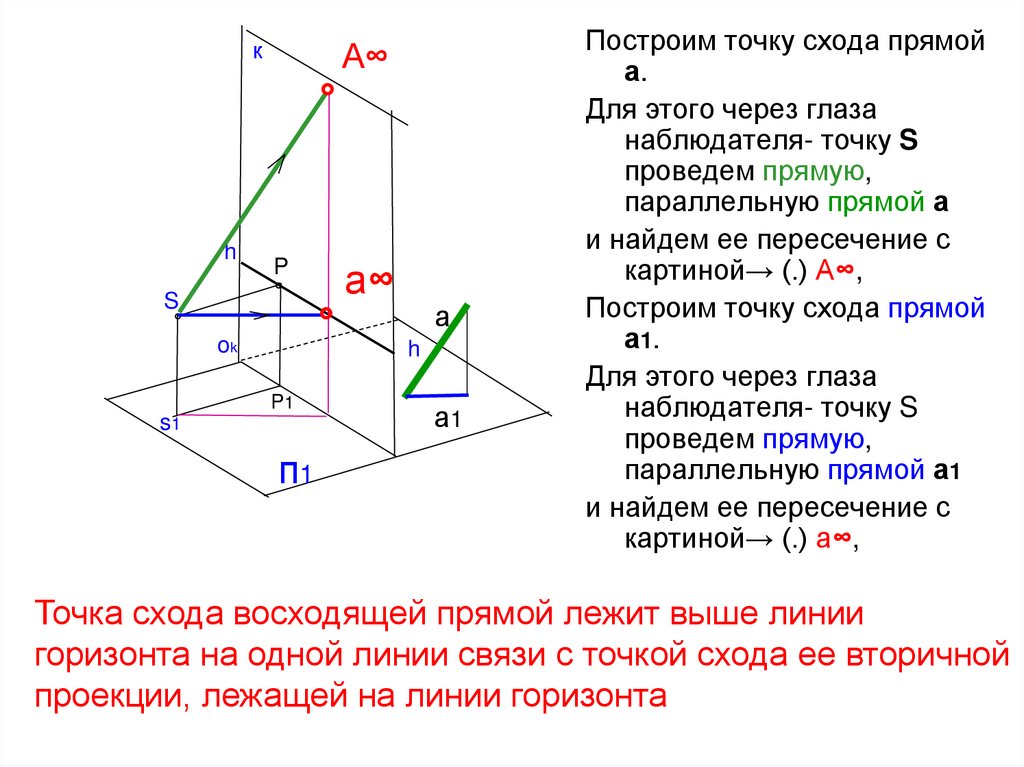
Построим точку схода прямой
а.
Для этого через глаза
наблюдателя- точку S
проведем прямую,
параллельную прямой а
и найдем ее пересечение с
картиной→ (.) А∞,
Построим точку схода прямой
а 1.
Для этого через глаза
наблюдателя- точку S
проведем прямую,
параллельную прямой а1
и найдем ее пересечение с
картиной→ (.) а∞,
Точка схода восходящей прямой лежит выше линии
горизонта на одной линии связи с точкой схода ее вторичной
проекции, лежащей на линии горизонта

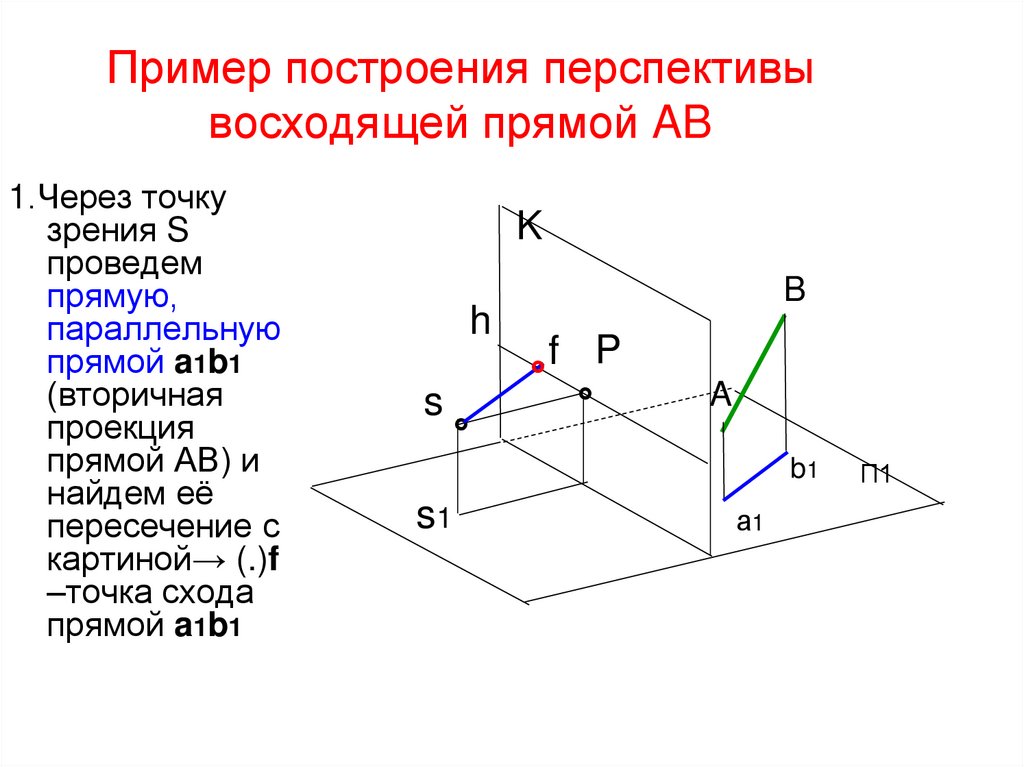
25. Пример построения перспективы восходящей прямой AB

1.Через точку
зрения S
проведем
прямую,
параллельную
прямой a1b1
(вторичная
проекция
прямой АВ) и
найдем её
пересечение с
картиной→ (.)f
–точка схода
прямой a1b1
K
h
s
°
B
f P
°
°
A
b1
s1
а1
П1

26. Пример построения перспективы восходящей прямой AB

2. Построим
картинный след
прямой а1b1 →
Mк (продлим её
до пересечения
с картиной).
Картинный
следперспектива
ближайшей
точки прямой.
K
h
s
°
B
f P
°
°
A
b1
s1
M°к
а1
П1

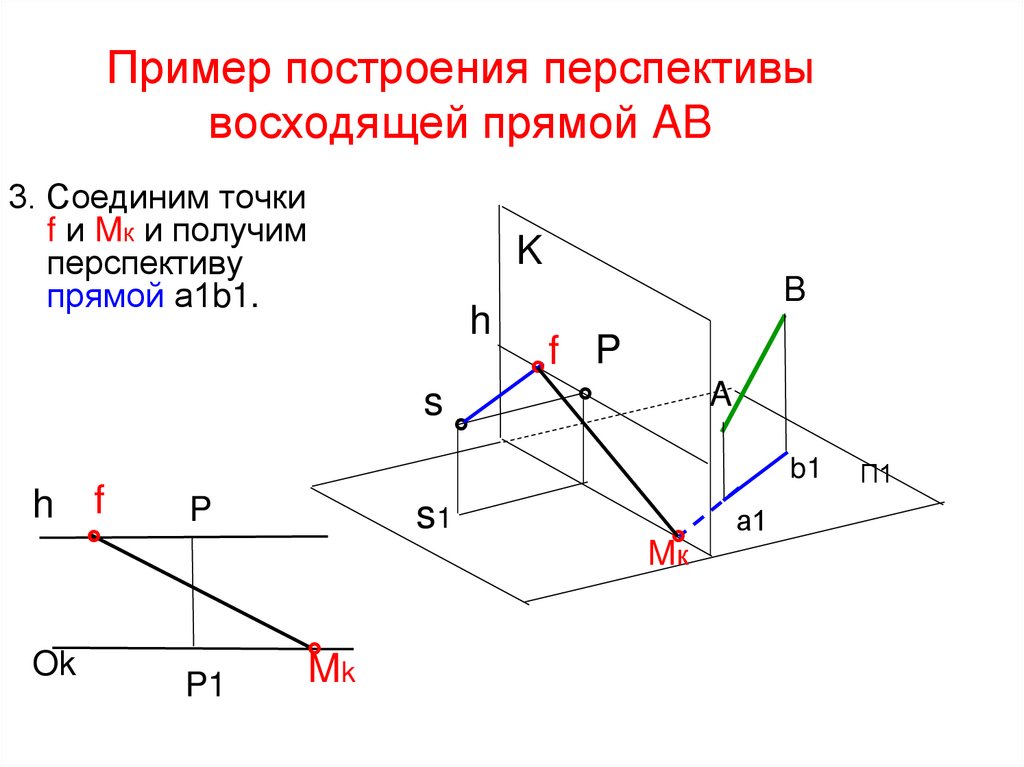
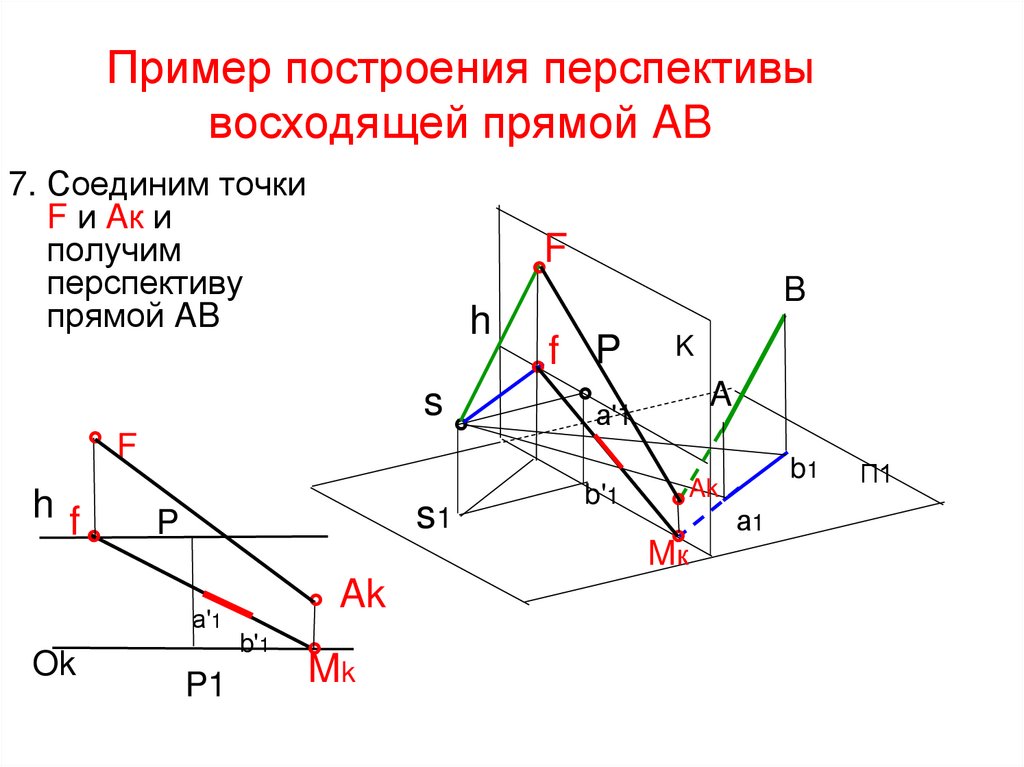
27. Пример построения перспективы восходящей прямой AB

3. Соединим точки
f и Mк и получим
перспективу
прямой а1b1.
K
h
s
°
B
f P
°
°
A
b1
h f
°
Ok
P
P1
s1
°Mk
M°к
а1
П1

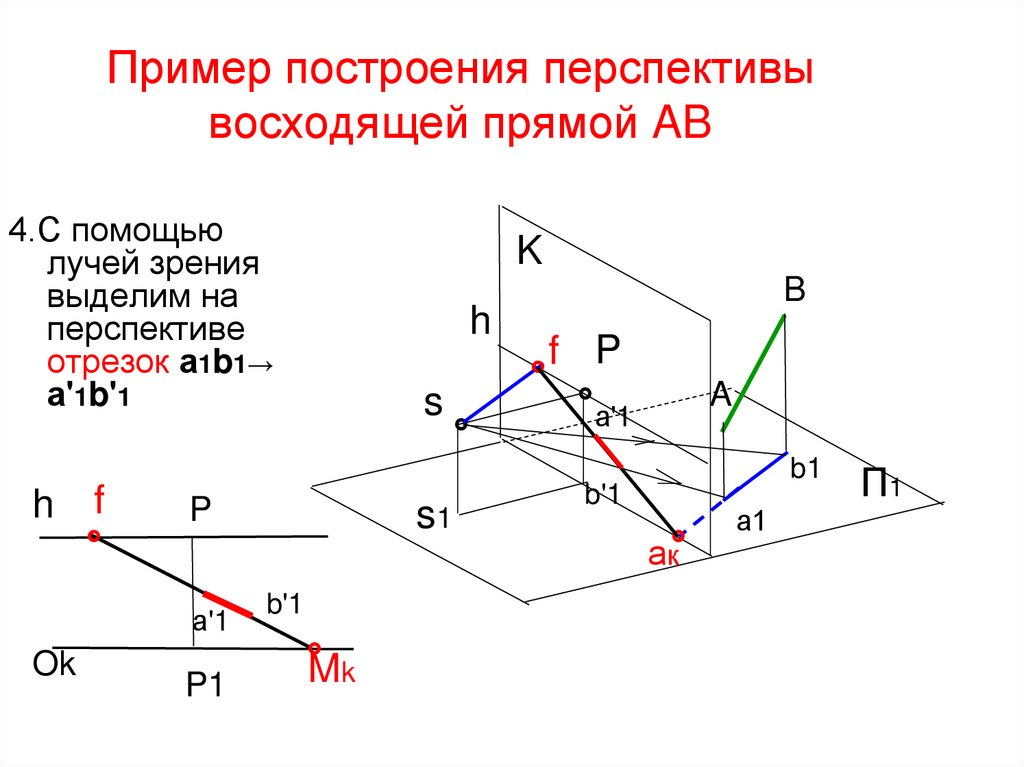
28. Пример построения перспективы восходящей прямой AB

4.С помощью
лучей зрения
выделим на
перспективе
отрезок а1b1→
а'1b'1
h f
°
h
s
P
а'1
Ok
K
P1
s1
b'1
°Mk
°
B
f P
°
°а'1
A
b1
b'1
ак°
а1
П1

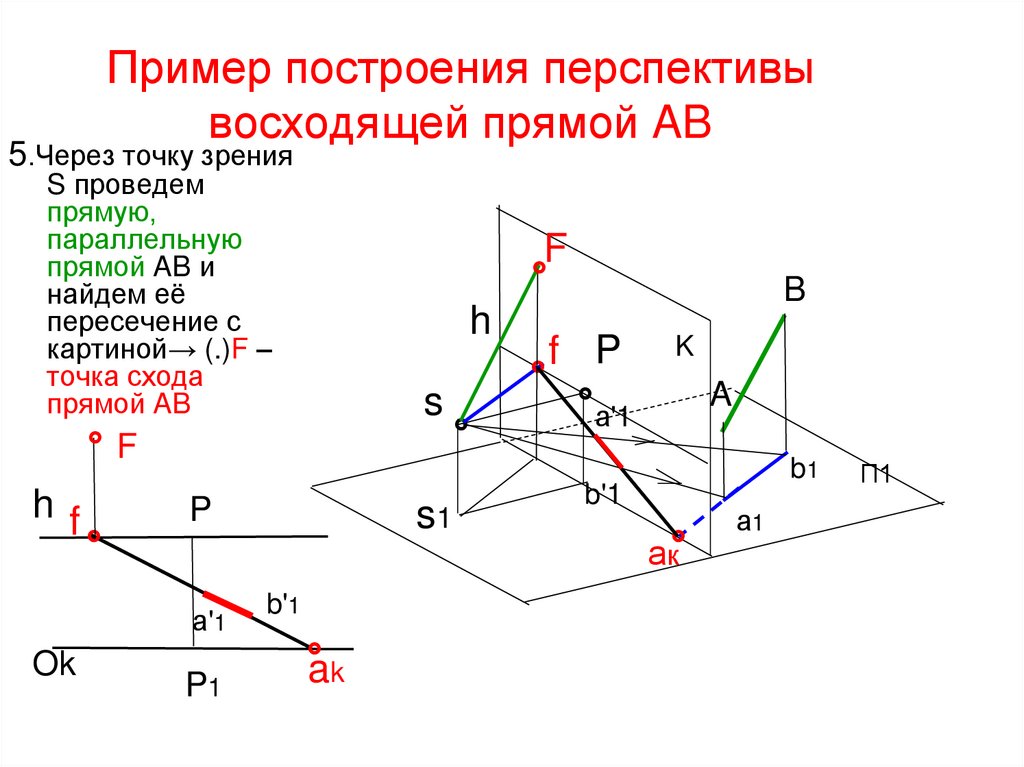
29. Пример построения перспективы восходящей прямой AB

5.Через точку зрения
S проведем
прямую,
параллельную
прямой AB и
найдем её
пересечение с
картиной→ (.)F –
точка схода
прямой AB
F
°
h
s
°F
hf
°
P
а'1
Ok
P1
s1
b'1
°ak
°
B
f P
°
°а'1
K
A
b1
b'1
ак°
а1
П1

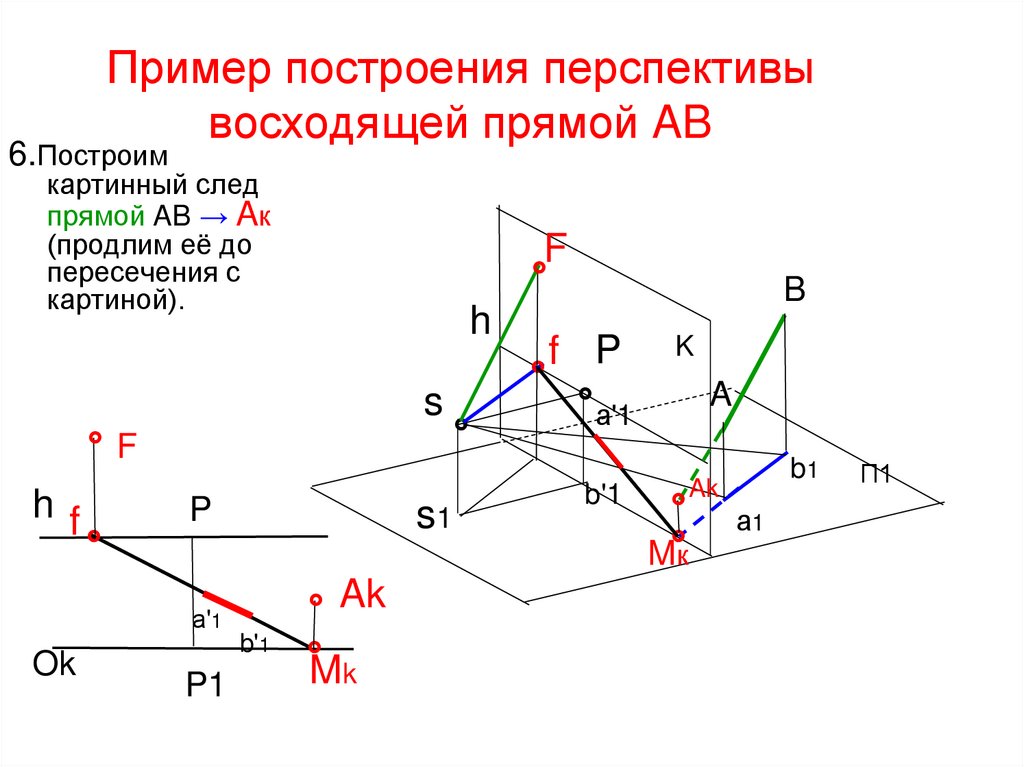
30. Пример построения перспективы восходящей прямой AB

6.Построим
картинный след
прямой AB → Aк
(продлим её до
пересечения с
картиной).
F
°
h
s
°F
hf
°
P
s1
а'1
Ok
b'1
P1
° Ak
°Mk
°
B
f P
°
° а'1
b'1
K
A
°
M°к
b1
Ak
а1
П1

31. Пример построения перспективы восходящей прямой AB

7. Соединим точки
F и Aк и
получим
перспективу
прямой AB
F
°
h
s
°F
hf
°
s1
P
а'1
Ok
b'1
P1
° Ak
°Mk
°
B
f P
°
° а'1
b'1
K
A
°
M°к
b1
Ak
а1
П1

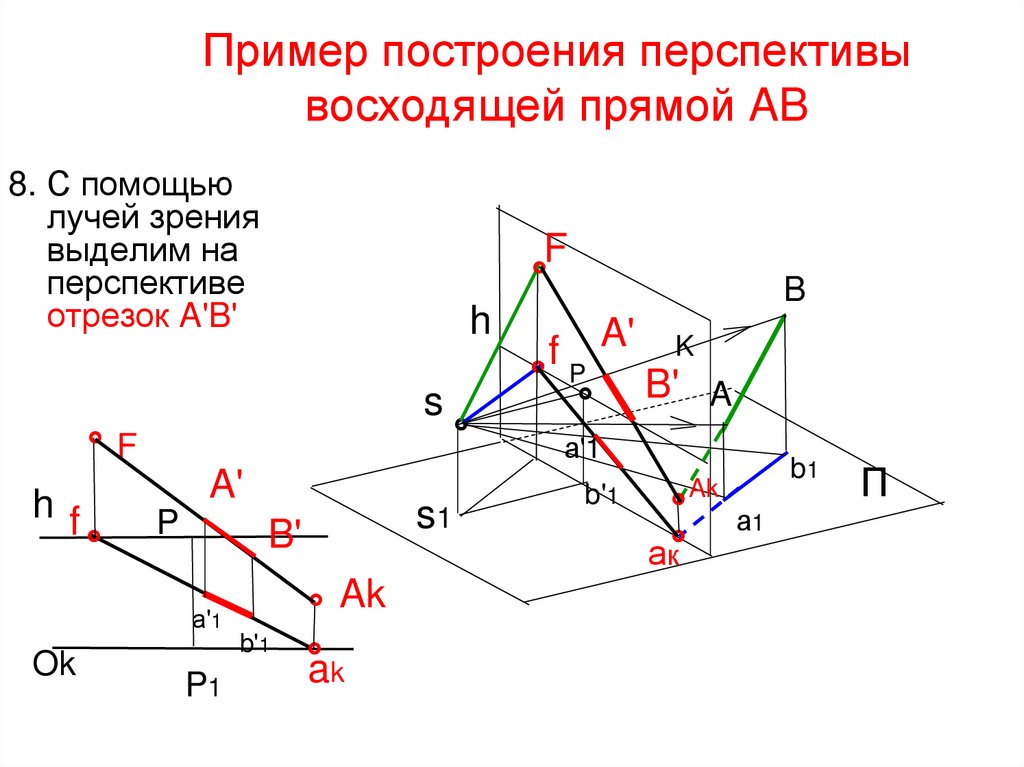
32. Пример построения перспективы восходящей прямой AB

8. С помощью
лучей зрения
выделим на
перспективе
отрезок A'B'
F
°
h
s
°F
hf
A'
°
P
B'
а'1
Ok
s1
b'1
P1
° Ak
°ak
°
B
f P A' K
°
° B' A
а'1
b'1
°
ак°
b1
Ak
а1
П

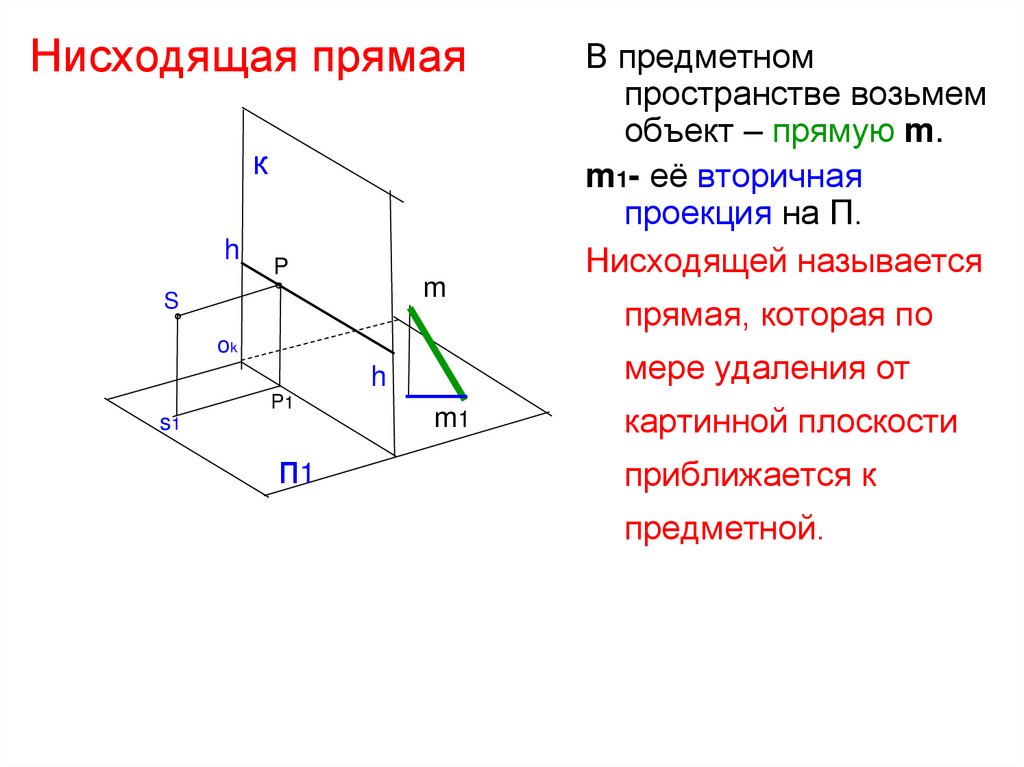
33. Нисходящая прямая

к
h
P
m
°
S
°
ok
s1
п1
прямая, которая по
мере удаления от
h
P1
В предметном
пространстве возьмем
объект – прямую m.
m1- её вторичная
проекция на П.
Нисходящей называется
m1
картинной плоскости
приближается к
предметной.

34.

к
h
P
°
S
°
ok
°
m∞
P1
m
h
m1
s1
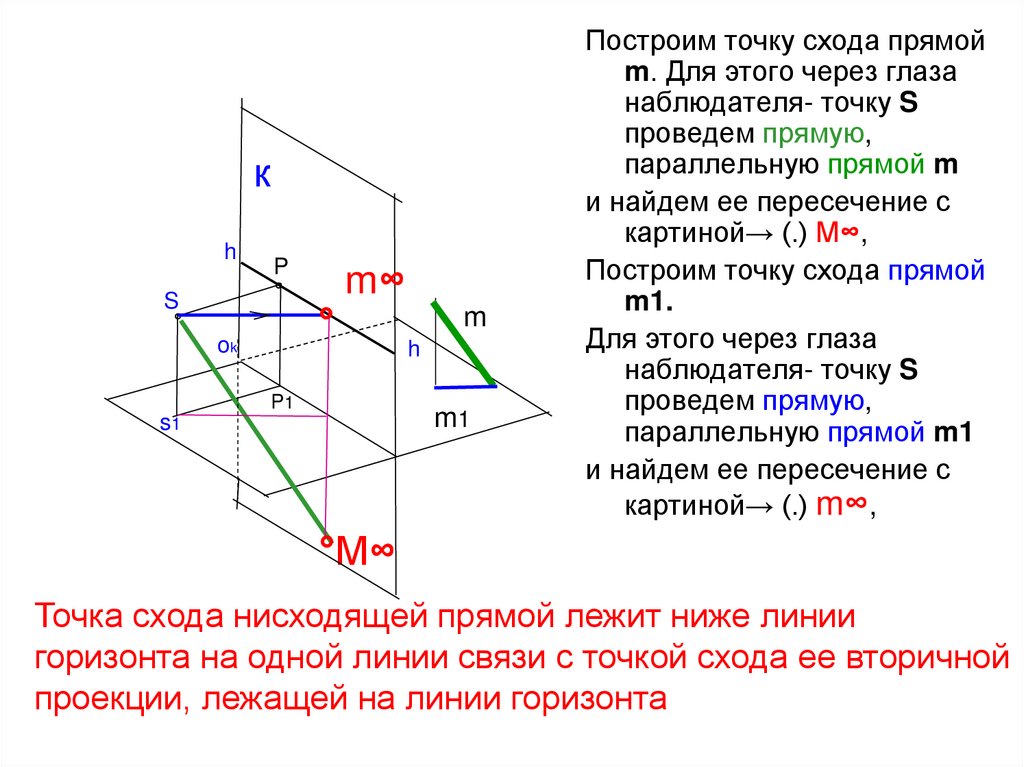
Построим точку схода прямой
m. Для этого через глаза
наблюдателя- точку S
проведем прямую,
параллельную прямой m
и найдем ее пересечение с
картиной→ (.) М∞,
Построим точку схода прямой
m1.
Для этого через глаза
наблюдателя- точку S
проведем прямую,
параллельную прямой m1
и найдем ее пересечение с
картиной→ (.) m∞,
°М∞
Точка схода нисходящей прямой лежит ниже линии
горизонта на одной линии связи с точкой схода ее вторичной
проекции, лежащей на линии горизонта

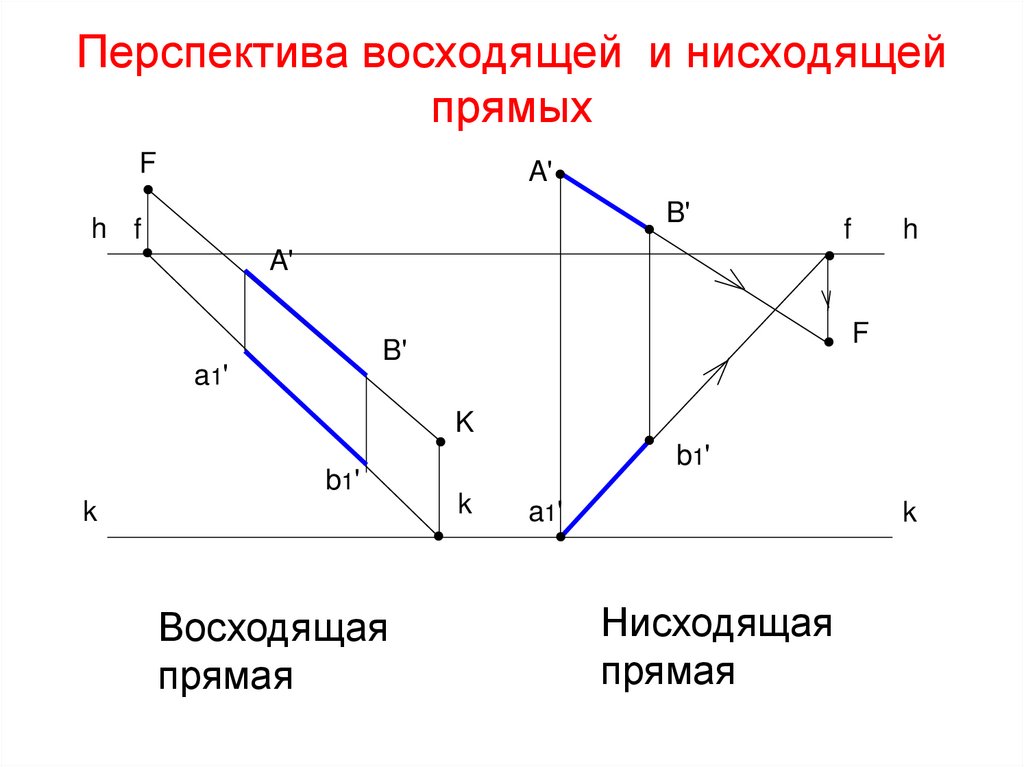
35. Перспектива восходящей и нисходящей прямых

F
A'
B'
h f
f
h
A'
F
B'
a 1'
K
b 1'
k
Восходящая
прямая
b 1'
k
a1 '
k
Нисходящая
прямая

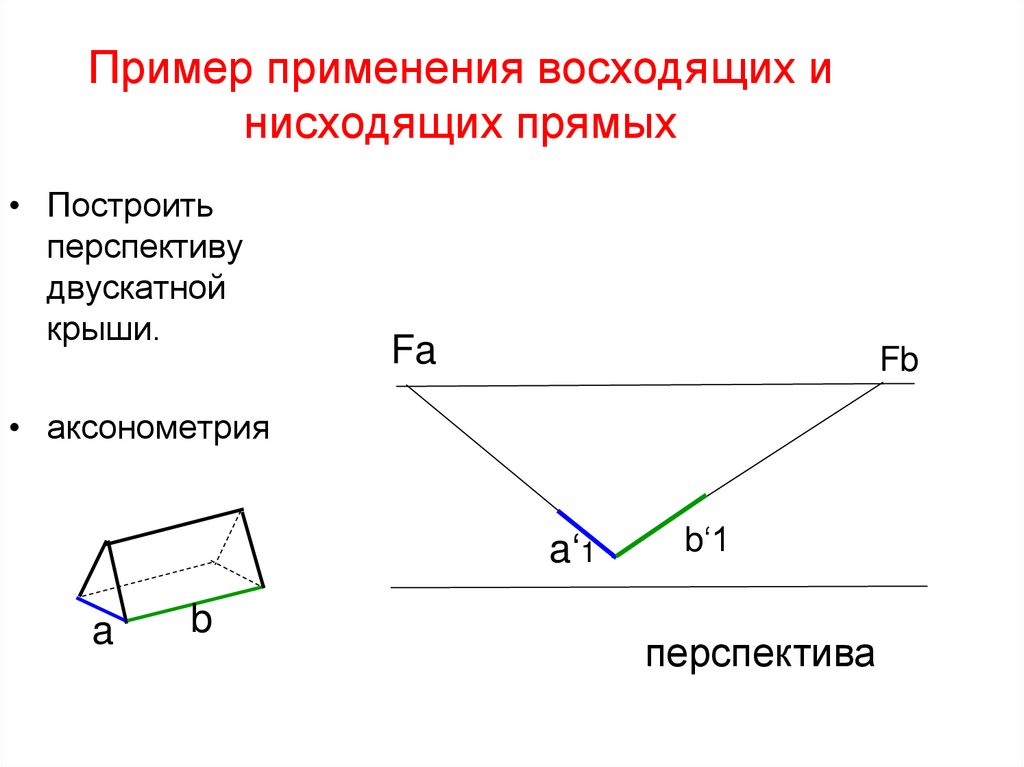
36. Пример применения восходящих и нисходящих прямых

• Построить
перспективу
двускатной
крыши.
Fa
Fb
• аксонометрия
a‘1
a
b
b‘1
перспектива

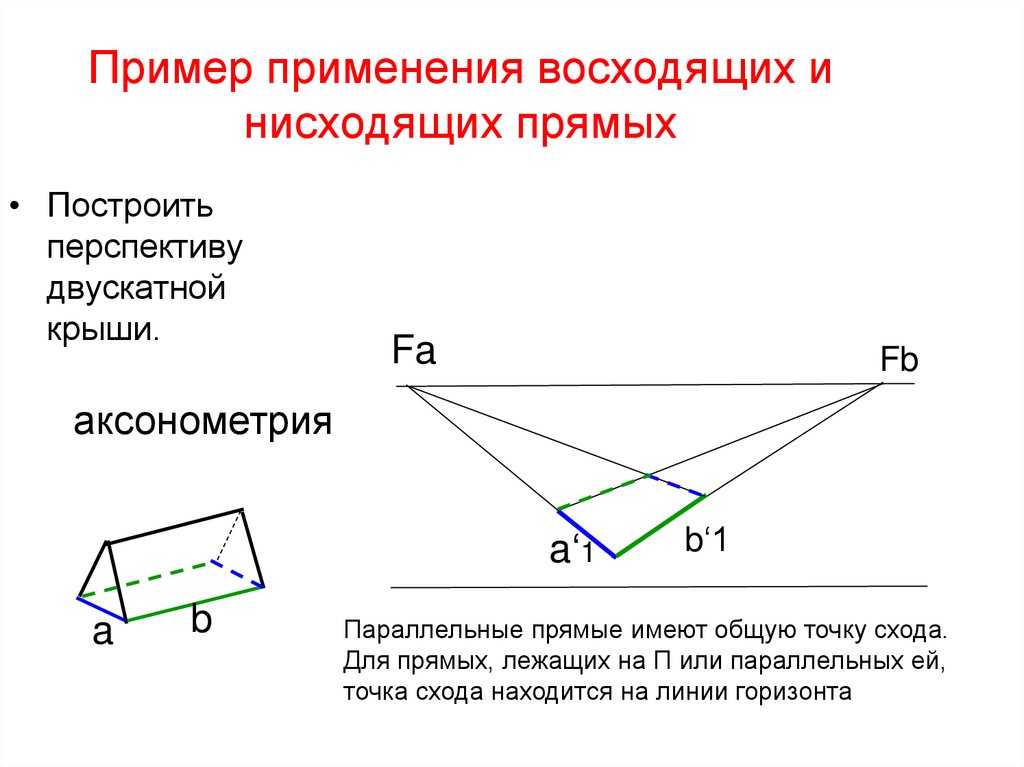
37. Пример применения восходящих и нисходящих прямых

• Построить
перспективу
двускатной
крыши.
Fa
Fb
аксонометрия
a‘1
a
b
b‘1
Параллельные прямые имеют общую точку схода.
Для прямых, лежащих на П или параллельных ей,
точка схода находится на линии горизонта

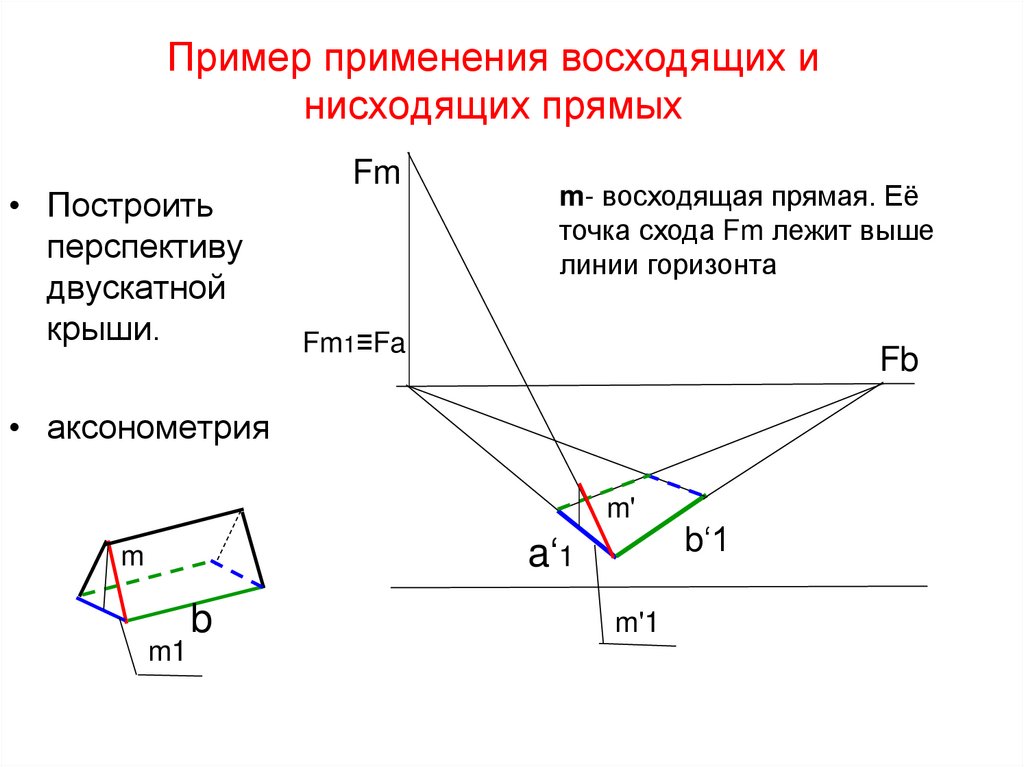
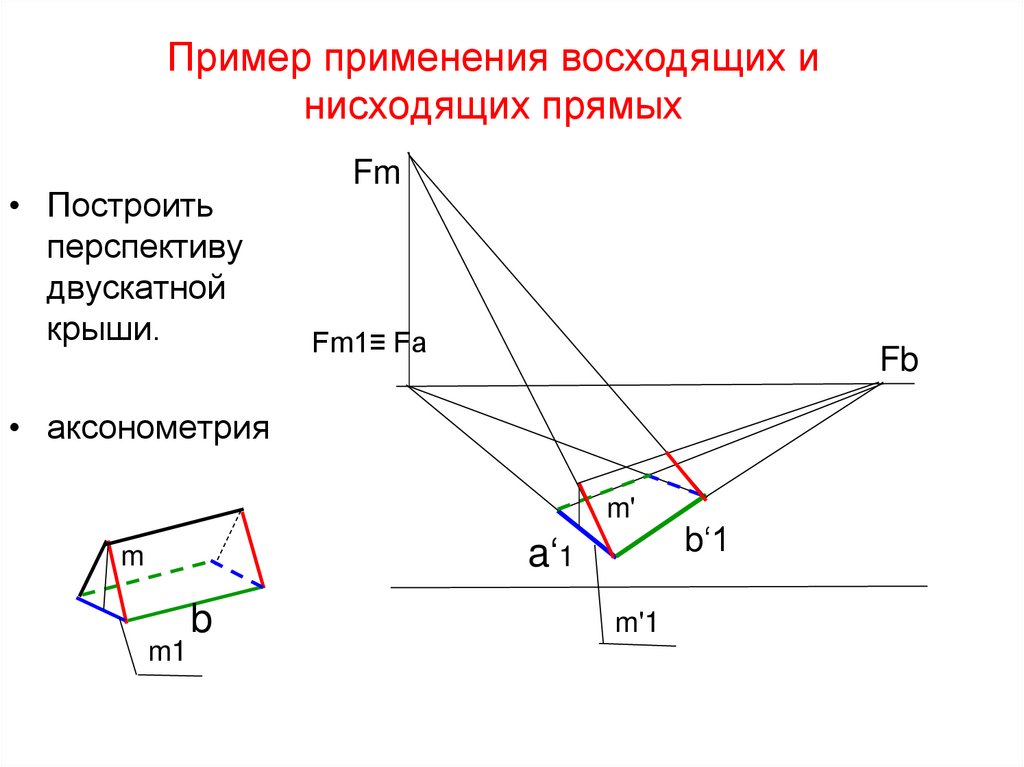
38. Пример применения восходящих и нисходящих прямых

• Построить
перспективу
двускатной
крыши.
Fm
m- восходящая прямая. Её
точка схода Fm лежит выше
линии горизонта
Fm1≡Fa
Fb
• аксонометрия
m'
b‘1
a‘1
m
m1
b
m'1

39. Пример применения восходящих и нисходящих прямых

• Построить
перспективу
двускатной
крыши.
Fm
Fm1≡ Fa
Fb
• аксонометрия
m'
b‘1
a‘1
m
m1
b
m'1

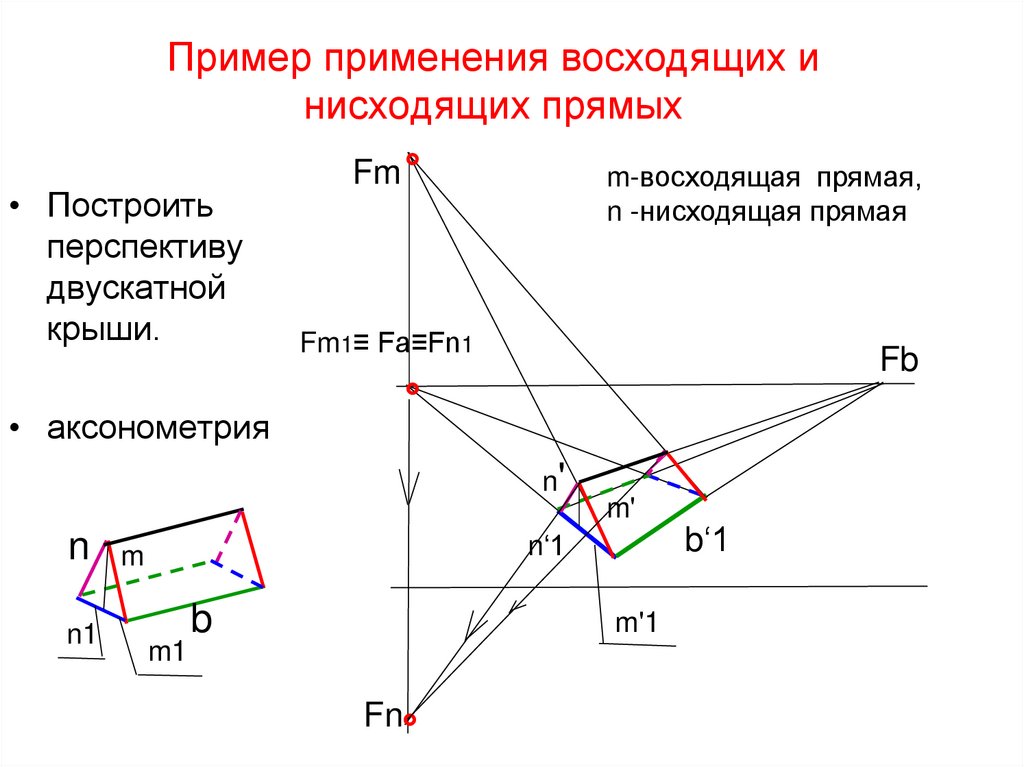
40. Пример применения восходящих и нисходящих прямых

• Построить
перспективу
двускатной
крыши.
• аксонометрия
Fm °
m-восходящая прямая,
n -нисходящая прямая
Fm1≡ Fa≡Fn1
Fb
°
n'
n
n1
m'
b‘1
n‘1
m
m1
b
m'1
Fn°

41. Перспективный эпюр

• Построить перспективу объекта можно еще
одним способом. Рассмотрим на примере
точки.
• Если провести через точку две
пересекающиеся прямые (запеленговать
точку), а потом построить перспективные
изображения этих прямых, то пересечение
перспектив данных прямых определит
перспективу данной точки.

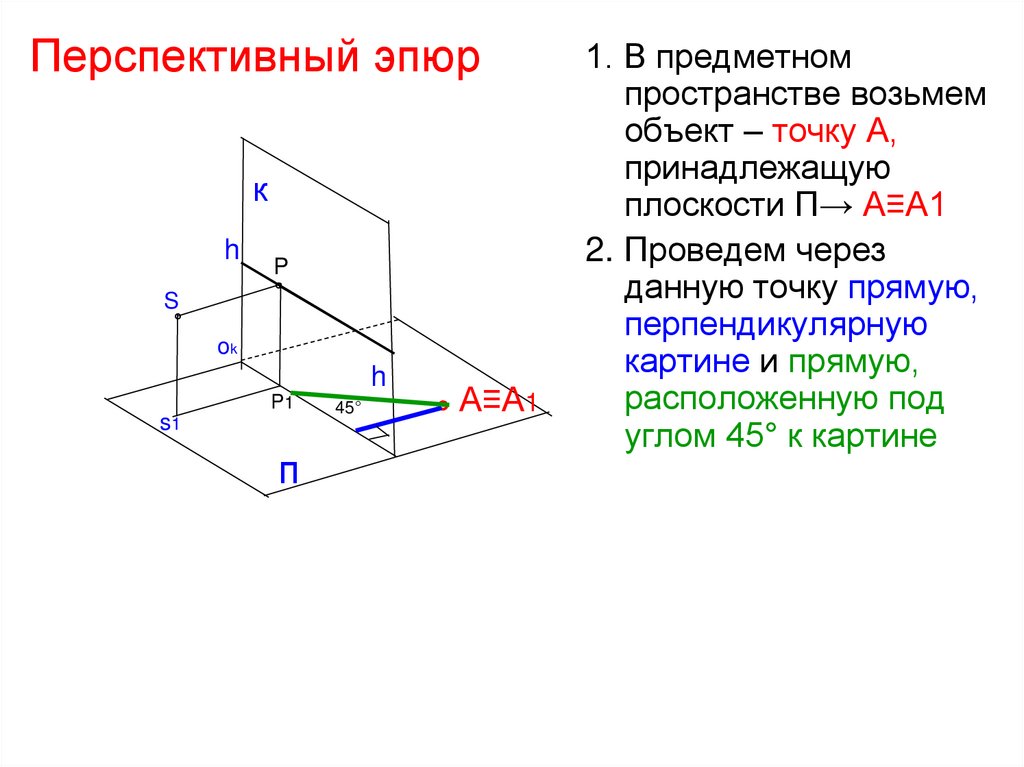
42. Перспективный эпюр

к
h
P
°
S
°
ok
h
P1
s1
п
45°
° А≡А1
1. В предметном
пространстве возьмем
объект – точку А,
принадлежащую
плоскости П→ А≡А1
2. Проведем через
данную точку прямую,
перпендикулярную
картине и прямую,
расположенную под
углом 45° к картине

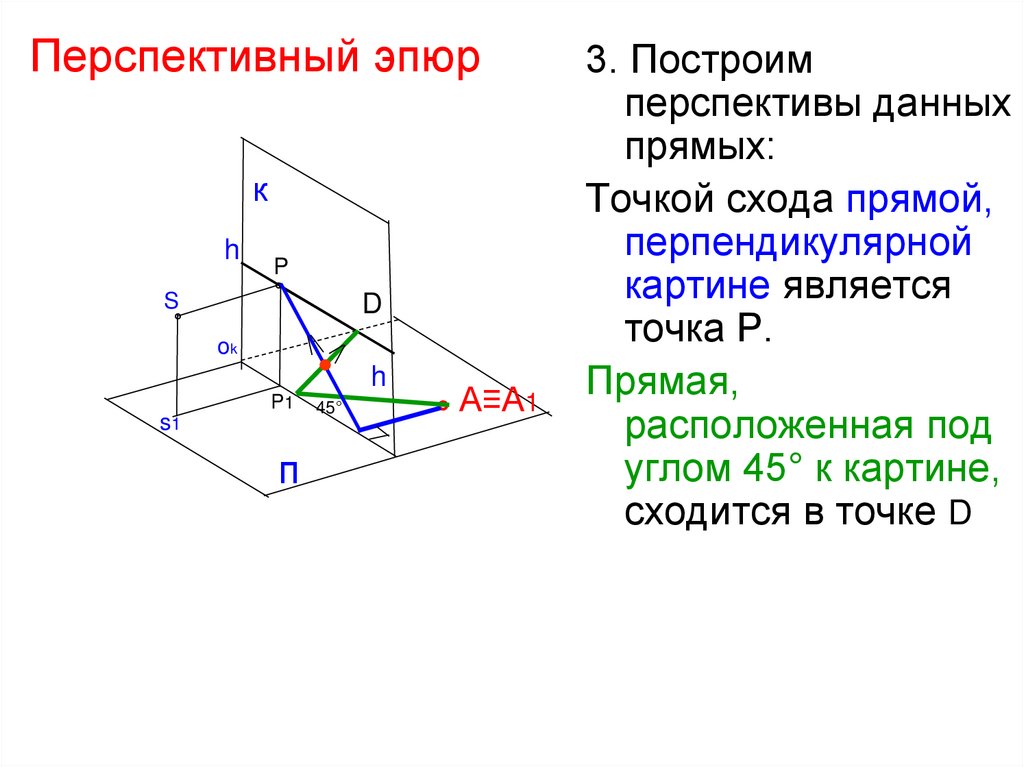
43. Перспективный эпюр

к
h
P
°
S
D
°
ok
P1
s1
п
45°
h
° А≡А1
3. Построим
перспективы данных
прямых:
Точкой схода прямой,
перпендикулярной
картине является
точка Р.
Прямая,
расположенная под
углом 45° к картине,
сходится в точке D

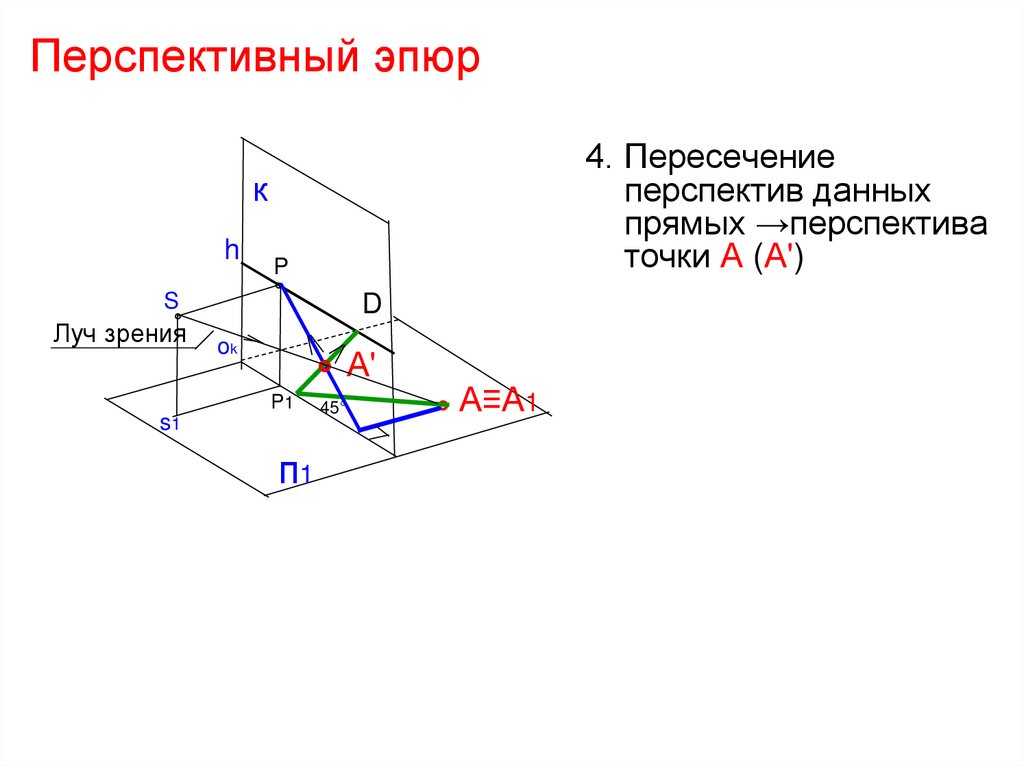
44. Перспективный эпюр

4. Пересечение
перспектив данных
прямых →перспектива
точки А (А')
к
h
P
°
S
D
°
Луч зрения
ok
А'
°
P1
45°
s1
п1
° А≡А1

45. Перспективный эпюр

к
h
P
°
S
D
°
Луч зрения
s1
ok
А'
°
P1
45°
45°
п1
° А≡А1
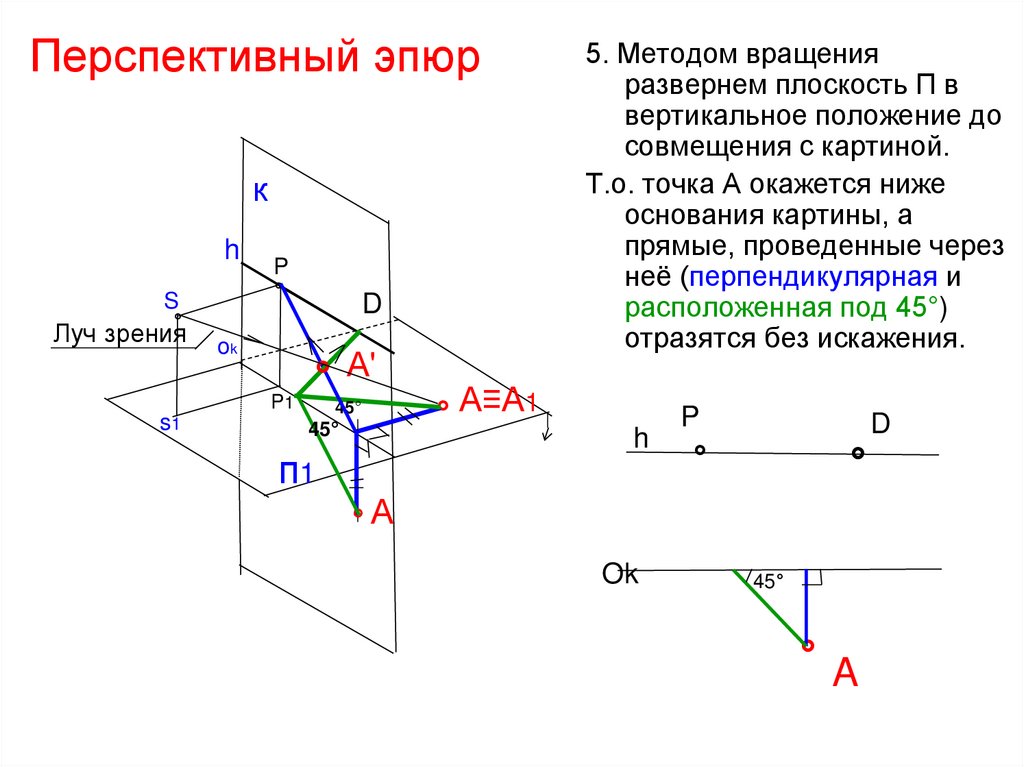
5. Методом вращения
развернем плоскость П в
вертикальное положение до
совмещения с картиной.
Т.о. точка А окажется ниже
основания картины, а
прямые, проведенные через
неё (перпендикулярная и
расположенная под 45°)
отразятся без искажения.
h
P
D
°
°
°А
Ok
45°
°A

46. Перспективный эпюр

к
h
P
°
S
D
°
Луч зрения
ok
P1
s1
п1
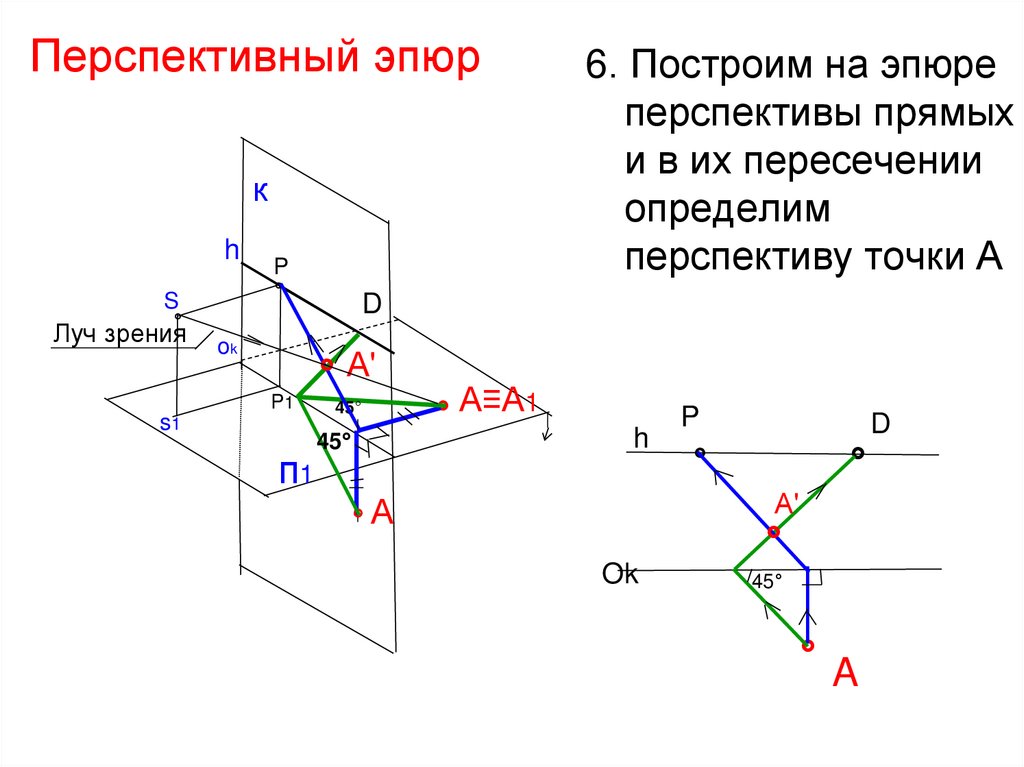
6. Построим на эпюре
перспективы прямых
и в их пересечении
определим
перспективу точки А
° А'
45°
45°
° А≡А1
h
P
D
°
°
А'
°А
Ok
°
45°
°A