ТИК Лекц 2

1.

ТЕОРИЯ
ИНФОРМАЦИИ И
КОДИРОВАНИЯ
Семес- Трудоемтр
кость,
кр.
1
3
Общий
объем
курса,
час.
Лекции,
час.
108
24
Практич. Лаборат. СРС,
Форма
занятия, работы, час. контроля,
час.
час.
Экз./зачет
8
16
24
36
Экзамен
Дисциплина для групп: М*-502, М*-512, М*-522,
М*-532, М*-562, М*-В01
Автор: доцент, к.т.н. Березкин Евгений Феофанович

2.

Обобщенный ряд Фурье
f ( x ) Ck k ( x ) ,
k 0
где
Ck
b
1
k
2
f ( x) ( x)dx ,
k
a
обладает следующим важным свойством: при заданной системе
функций k (x) и при фиксированном числе слагаемых ряда, он
обеспечивает наилучшую аппроксимацию данной функции f (x ) .
Это означает, что среднеквадратическая ошибка, под которой
подразумевается величина
2
E f ( x) ak k ( x) dx ,
k 0
a
достигает минимума, когда коэффициенты ak Ck .
b
N

3.

2
N
E f ( x) ak k ( x) dx
k 0
a
b
Таким образом,
b
N
b
N
b
a
k 0
a
k 0
a
Emin f 2 ( x)dx 2 Ck f ( x) k ( x)dx Ck2 2k ( x)dx
b
N
f 2 ( x)dx 2 Ck2 k
a
2
k 0
N
Ck2 k
b
2
k 0
N
f 2 ( x)dx Ck2 k .
2
k 0
a
Ортогональная система называется полной, если увеличением
числа членов в ряде среднеквадратическую ошибку Emin можно
сделать сколь угодно малой.
Условие полноты
b
f ( x)dx C
2
k 0
a
2
k
2
k
приобретает энергетический смысл. Действительно, если под I (t )
подразумевается электрическое колебание (ток), то
t2
Э I (t )dt Ck2 k
2
t1
k 0
2

4.

есть не что иное, как энергия сигнала в промежутке [t1 , t 2 ] (при
условии, что сопротивление, в котором выделяется энергия, равно 1
Ом). При этом имеется в виду, что промежуток времени [t1 , t 2 ] , в
котором
определяется
энергия,
является
интервалом
ортогональности.
Очевидно, что средняя за время t2 t1 мощность сигнала равна
Э
1 2
2
I (t )
Ck k .
t2 t1 t2 t1 k 0
2
Для
бесконечной
системы
функций
..., m ( x),..., k ( x),..., 1 ( x), 0 ( x), 1 ( x),..., k ( x),..., m ( x),... ,
принимающих комплексные значения, приведенные выше
определения обобщаются следующим образом:
– условие ортогональности
b
*
(
x
)
k
m ( x)dx 0 при k m ;
a
– квадрат нормы функции
b
b
k ( x) k ( x) ( x)dx k ( x) dx ;
2
2
*
k
a
a

5.

– коэффициент Фурье
Ck
1
k
b
*
f
(
x
)
( x)dx ;
2
k
a
– средняя мощность
1
2
2
.
I (t )
C
k
k
t2 t1 k
2
В этих выражениях *k ( x) обозначает функцию, комплексносопряженную функции k (x) .
1.2. ЧАСТОТНОЕ ПРЕДСТАВЛЕНИЕ ДЕТЕРМИНИРОВАННЫХ
ПЕРИОДИЧЕСКИХ СИГНАЛОВ
При разложении периодического колебания x ( t ) в ряд Фурье в
качестве ортогональной системы берут [3]
(1.5)
1, cos 0t , sin 0t , cos 2 0t , sin 2 0t ,..., cos k 0t , sin k 0t ,...
или
..., e j 2 0t , e j 0t ,1, e j 0t , e j 2 0t ,... .
(1.6)

6.

Интервал ортогональности в обоих случаях
совпадает с
T T
, .
2 2
периодом T 2 / 0 функции x ( t ) , т.е
Система функций (1.5) приводит к тригонометрической форме
ряда Фурье, а система (1.6) – к комплексной форме. Между этими
двумя формами существует простая связь.
Воспользуемся сначала ортогональной системой (1.6). Тогда ряд
Фурье должен быть записан в форме
x(t ) C k e jk 0t .
k
Коэффициенты Фурье определяются с помощью формул,
( k
приведенных в подразделе 1.1
2
T
2
e jk 0t e jk 0t dt T ),
Ck
T
2
T
2
1
jk 0 t
x
(
t
)
e
dt .
T T
(1.7)
2
В этих выражениях учтено, что функции e
комплексно-сопряженная функция e
jk 0 t
.
jk 0 t
соответствует

7.

Коэффициенты Ck в общем случае являются комплексными
величинами.
Подставив
в
(1.7)
e jk 0t cos k 0 t j sin k 0 t ,
получим
Ck
T
2
T
2
1
1
x
(
t
)
cos
k
tdt
j
x(t ) sin k 0tdt Ckc jCks .
0
T T
T T
2
2
Часто бывает, что коэффициенты Ck удобно записывать в
форме Ck Ck e j k , где Ck Ckc2 Cks2 , k arctg
Модуль
Ck
C ks
.
Ckc
является функцией четной относительно k ,
аргумент k – нечетной (последнее вытекает из того, что C kc
является четной, а C ks – нечетной функциями k ).
Общее выражение ряда можно привести к виду
x(t ) Ck e j ( k 0t k ) .
k
(1.8)

8.

Теперь нетрудно перейти к тригонометрической форме ряда
Фурье. Выделив из ряда (1.8) пару слагаемых, соответствующую
какому-либо заданному значению k , и учтя соотношения
k k , C k Ck , получим для суммы этих слагаемых
C k e j ( k 0t k ) Ck e j ( k 0t k ) Ck e j ( k 0t k ) e j ( k 0t k )
2 Ck cos( k 0t k ).
Отсюда видно, что при переходе к тригонометрической форме
ряд (1.8) необходимо записать так:
x(t ) C0 2 Ck cos( k 0t k ) .
(1.9)
k 1
После перехода к тригонометрической форме (1.9) понятие
”отрицательная частота” теряет смысл. Коэффициент C 0 не
удваивается, так как в спектре периодического сигнала
составляющая с нулевой частотой не имеет ”дублера”.
Ck
Смысл
удвоения
коэффициентов
Фурье
в
тригонометрическом ряду при k 1 становится ясным из
рассмотрения векторной диаграммы, приведенной на рис. 1.3.

9.

Вещественная функция 2 Ck cos(k 0t k ) получается как
сумма проекций на горизонтальную ось ОВ двух векторов длиной
во взаимно
Ck , вращающихся с угловой частотой k 0
противоположных направлениях.
Вектор, вращающийся против часовой стрелки, соответствует
положительной частоте, а вектор, вращающийся по часовой
стрелке, – отрицательной.
k 0
2 Ck cos(k 0t k )
Ck
k 0t k
О
(k 0t k )
C k
k 0
Рис. 1.3. Векторная диаграмма
В

10.

Вместо выражения (1.9) в технической литературе чаще
используется следующая форма записи
x(t )
x(t ) C0 2 Ck cos( k 0t k )
A0
Ak cos( k 0t k )
2
k 1
k 1
A0
( Ak cos k cos k 0t Ak sin k sin k 0t )
2
k 1
(1.10)
A0
(ak cos k 0t bk sin k 0t ) ,
2
k 1
где
A0
2
–
постоянная
Ak cos( k 0t k ) – k-я
составляющая
функции
x (t ) ;
гармоническая составляющая;
Ak , k 0 , k – амплитуда, частота и начальная фаза k-й
2
гармонической составляющей; 0
– частота основной
T
гармоники (T – период колебаний).

11.

Из сопоставления (1.9) и (1.10) видно, что модуль амплитуды kй гармоники Ak
связан с модулем коэффициента Ck
A0
Ak 2 Ck
C0 ) .
2
Ряд Фурье (1.10) с учетом свойств периодической функции x ( t )
приобретает еще более простой вид:
соотношениями
(
x(t ) bk sin k 0t
– нечетная функция,
k 1
A0
x(t )
ak cos k 0t
2 k 1
Коэффициенты a k
выражениями
и bk
– четная функция.
вычисляются в соответствии с
T /2
2
ak 2Ckc Ak cos k
x(t ) cos( k 0t )dt ,
T T / 2
T /2
2
bk 2Cks Ak sin k
x(t ) sin( k 0t )dt
T T / 2

12.

и связаны между собой формулой Ak
a k2 bk2 .
Соответственно комплексная форма ряда Фурье принимает вид
1
1
jk 0t
x(t ) Ak e
Ak e j ( k 0t k ) ,
2 k
2 k
где
Ak ak jbk Ak e j k
–
комплексная
(1.11)
амплитуда
гармонической составляющей частоты k 0 , вычисляемая по
формуле
T /2
T /2
T /2
2
2
2
jk 0t
Ak
x
(
t
)
e
dt
x
(
t
)
cos(
k
t
)
dt
j
x(t ) sin( k 0t )dt ;
0
T T / 2
T T / 2
T T / 2
bk
– начальная фаза, определяемая на интервале [
k arctg
ak
T /2
A 1
, ]; 0
x(t )dt – постоянная составляющая.
2 T T / 2

13.

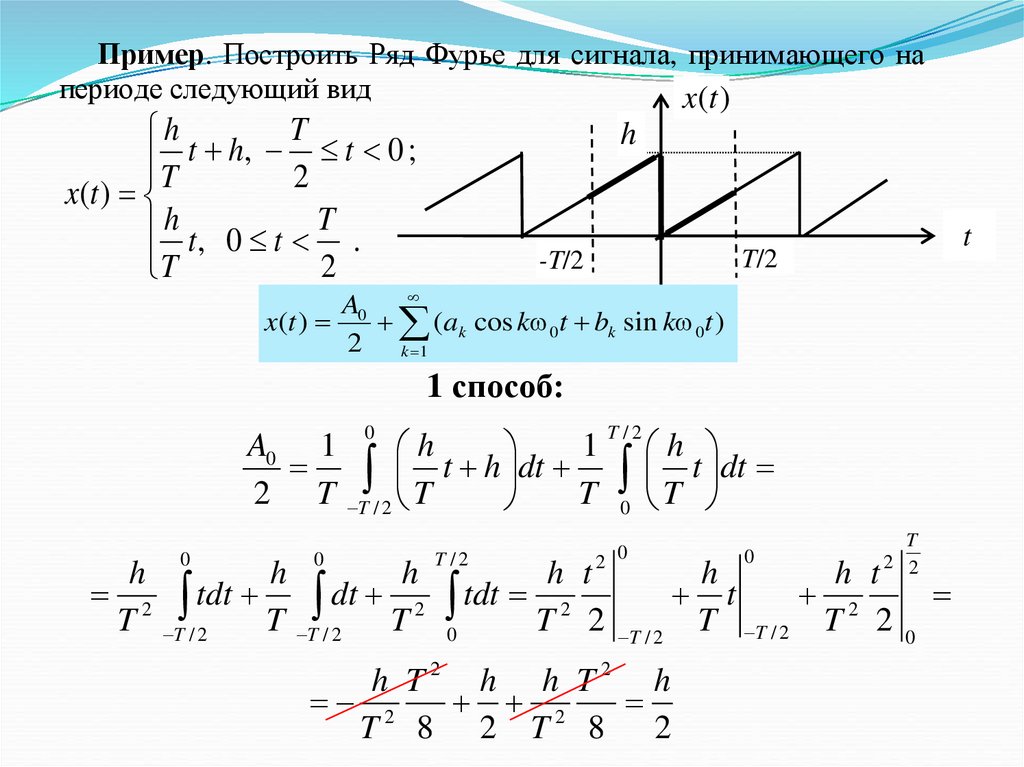
Пример. Построить Ряд Фурье для сигнала, принимающего на
периоде следующий вид
x(t )
T
h
T t h, 2 t 0 ;
x(t )
h t, 0 t T .
T
2
h
t
T/2
-T/2
A0
x(t )
(ak cos k 0t bk sin k 0t )
2 k 1
1 способ:
A0 1
1 h
h
t
h
dt
t dt
2 T T / 2 T
T 0 T
0
0
0
T /2
T /2
2 0
0
T
2 2
h
h
h
h t
h
h t
2 tdt
dt 2 tdt 2
t
2
T T / 2
T T / 2 T 0
T 2 T / 2 T T / 2 T 2 0
h T2 h h T2 h
2
2
T 8 2 T 8 2

14.

2
2 h
h
ak
t
h
cos
k
tdt
t cos k 0tdt
0
T T / 2 T
T 0 T
0
0
T /2
0
T /2
2h
2h
2h
2 t cos k 0tdt
cos k 0tdt 2 t cos k 0tdt
T T / 2
T T / 2
T 0
0
0
T /2
2h
1
2h 1
2h
1
2
td sin k 0t
sin k 0t
2
td sin k 0t
T T / 2 k 0
T k 0
T 0 k 0
T / 2
0
0
2h T
2h T
2 T
0
t sin k 0t
2
sin
k
tdt
sin
k
0
T / 2
T k 2
T 2
T / 2
T k 2
T /2
2h T
T /2
t sin k 0t
2
sin k 0tdt
0
T k 2
0
0
0
h T
h T
2 T
1
2 T
1
0
T /2
sin k
sin k
cos k 0t T / 2
cos k 0t 0
Tk 2
T 2 k 0
T 2 k 0
Tk 2
h T
2 T h T
2 T
1 0
1 cos k
cos k
Tk k 2
T 2 Tk k 2
T 2

15.

2
2 h
h
bk
t
h
sin
k
tdt
t sin k 0tdt
0
T T / 2 T
T 0 T
0
0
T /2
0
T /2
2h
2h
2h
2 t sin k 0tdt
sin
k
tdt
t sin k 0tdt
0
2
T T / 2
T T / 2
T 0
0
0
T /2
2h
1
2h 1
2h
1
2
td cos k 0t
cos k 0t
2
td cos k 0t
T T / 2 k 0
T k 0
T 0 k 0
T / 2
0
2h T
2h T
2 T
0
2
t
cos
k
t
cos
k
tdt
1
cos
k
0 T / 2
0
T k 2
T 2
T / 2
T k 2
T /2
2h T
T /2
t cos k 0t cos k 0tdt
2
0
T k 2
0
0
2h T
h T
2 T
1
0
cos k
1 cos k
sin k 0t T / 2
Tk 2
T 2 k 0
T k 2
0
h T
2 T
1
T /2
cos k
sin k 0t 0
Tk 2
T 2 k 0
h
h
h
h
h
cos k
cos k cos k
k 2
k 2
k k
k

16.

A0
x(t )
(ak cos k 0t bk sin k 0t )
2 k 1
h h 1
sin k 0t
2 k 1 k
2 способ:
h
1
x(t ) ( 1) k 1 sin k 0t
k 1
k
x(t )
2h
1
1
sin( 0 t ) sin( 2 0 t ) sin( 3 0 t ) ...
2
3
h
1.
2
2. e -j t0 k 0t0
2 T
k
k
T 2
k k

17.

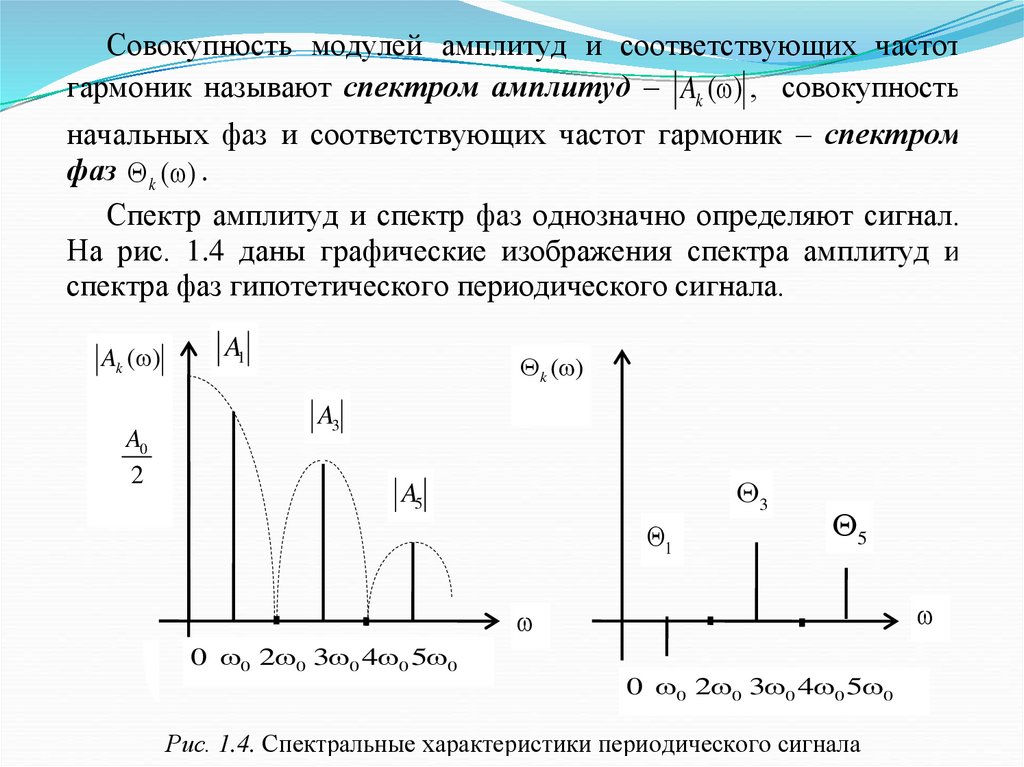
Совокупность модулей амплитуд и соответствующих частот
гармоник называют спектром амплитуд – Ak ( ) , совокупность
начальных фаз и соответствующих частот гармоник – спектром
фаз k ( ) .
Спектр амплитуд и спектр фаз однозначно определяют сигнал.
На рис. 1.4 даны графические изображения спектра амплитуд и
спектра фаз гипотетического периодического сигнала.
Ak ( )
A0
2
A1
k ( )
A3
3
A5
1
5
0 0 2 0 3 0 4 0 5 0
0 0 2 0 3 0 4 0 5 0
Рис. 1.4. Спектральные характеристики периодического сигнала

18.

Характерной особенностью спектров периодического сигнала
является его дискретность. Расстояние между соседними
спектральными линиями одинаковое и равно частоте основной
гармоники.
Пример. Найти спектр периодической последовательности
прямоугольных импульсов (рис. 1.5)
T
h, iT t 2 iT ;
x(t )
h, T iT t iT , i 0, 1, 2,... ,
2
называемой меандром
x(t )
h
t
-T/2
T/2
Рис. 1.5. Меандр

19.

Поскольку функция x ( t ) нечетная, разложение будем искать в
виде ( a k = 0)
x(t ) bk sin k 0t .
k 1
Спектр амплитуд вычисляется следующим образом:
T /2
T /2
2
4h
bk
x(t ) sin( k 0t ) dt
sin( k 0t )dt
T T / 2
T 0
T /2
4h 1
2h
cos k 0t
(cos k 1)
0
T k 0
k
4h
, k 1,3,5,...;
k
0, k 2,4,6,... .
Спектр фаз имеет вид
/2
bk
k arctg 0 .
0
/ 2

20.

Окончательно тригонометрическая форма обобщенного ряда
Фурье будет иметь вид
4h
1
1
x(t )
(sin 0t sin 3 0t sin 5 0t ...) .
3
5
Спектральные характеристики меандра приведены на рис. 11.1.
Ak ( )
k ( )
0 3 0 5 0 7 0
4h/
4h/3
- /2
4h/5
4h/7
0 3 0 5 0 7 0
A0
x(t )
Ak cos(k 0t k )
2 k 1
Рис. 11.1. Спектр амплитуд и спектр фаз меандра

21.

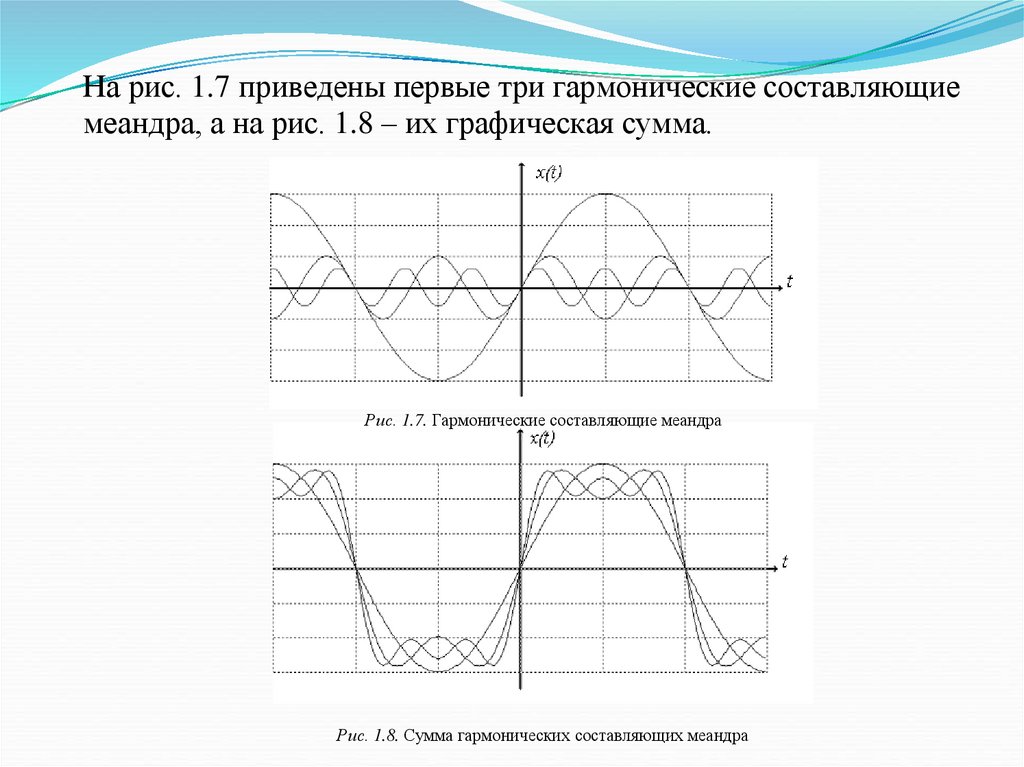
На рис. 1.7 приведены первые три гармонические составляющие
меандра, а на рис. 1.8 – их графическая сумма.
Рис. 1.7. Гармонические составляющие меандра
Рис. 1.8. Сумма гармонических составляющих меандра

22.

1
2
3
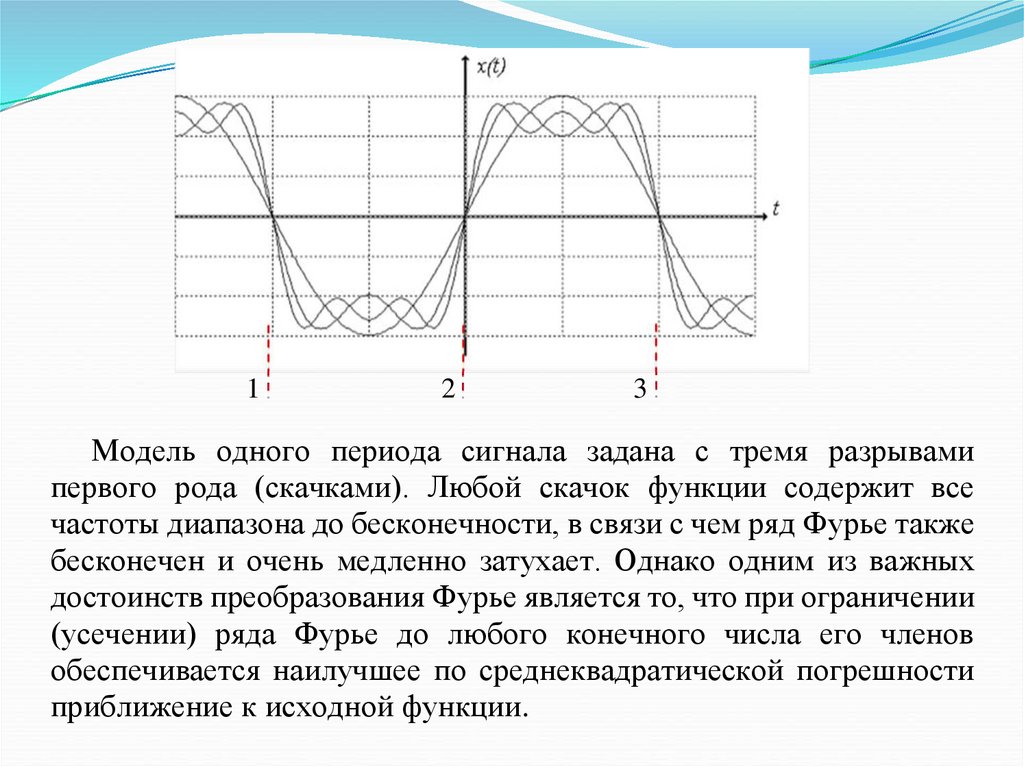
Модель одного периода сигнала задана с тремя разрывами
первого рода (скачками). Любой скачок функции содержит все
частоты диапазона до бесконечности, в связи с чем ряд Фурье также
бесконечен и очень медленно затухает. Однако одним из важных
достоинств преобразования Фурье является то, что при ограничении
(усечении) ряда Фурье до любого конечного числа его членов
обеспечивается наилучшее по среднеквадратической погрешности
приближение к исходной функции.

23.

1.3. НОСИТЕЛИ ИНФОРМАЦИИ И ВИДЫ МОДУЛЯЦИИ
Нанесение информации на материальный носитель путем
изменения одного из параметров физического процесса в
соответствии с законом изменения полезного сигнала называется
модуляцией. Модулированный материальный носитель можно
трактовать как сигнал, параметр которого содержит информацию
[5].
Для образования таких сигналов используются (рис. 1.9)
фиксированный уровень, колебание и импульсы любой физической
природы. В исходном состоянии эти носители представляют собой
как бы чистую поверхность, подготовленную к нанесению
необходимых данных – модуляции. Последняя заключается в том,
что изменяется какой-либо параметр носителя в соответствии с
передаваемой информацией. Эти параметры будем называть
информационными.

24.

а)
б)
в)
x(t )
x(t )
x(t )
A
A
A
T
код k
t
t
t
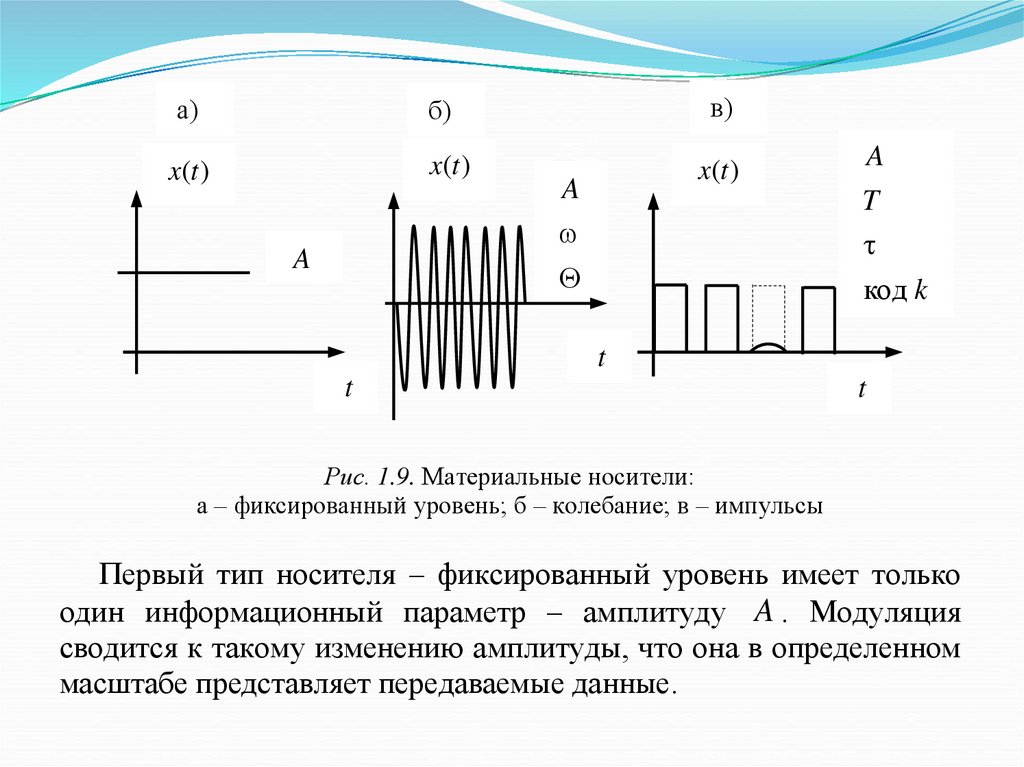
Рис. 1.9. Материальные носители:
а – фиксированный уровень; б – колебание; в – импульсы
Первый тип носителя – фиксированный уровень имеет только
один информационный параметр – амплитуду A . Модуляция
сводится к такому изменению амплитуды, что она в определенном
масштабе представляет передаваемые данные.

25.

Второй тип носителя – колебание содержит три параметра:
2
амплитуду A , фазу и частоту
.
T
Третий тип носителя – последовательность импульсов
представляет еще большие возможности. Здесь параметрами
модуляции
могут
быть:
амплитуда
A,
частота
f
1
,
T
длительность импульсов и комбинация импульсов и пауз,
определяющая код k .
Перечень основных видов модуляции приведен на рис. 1.10.

26.

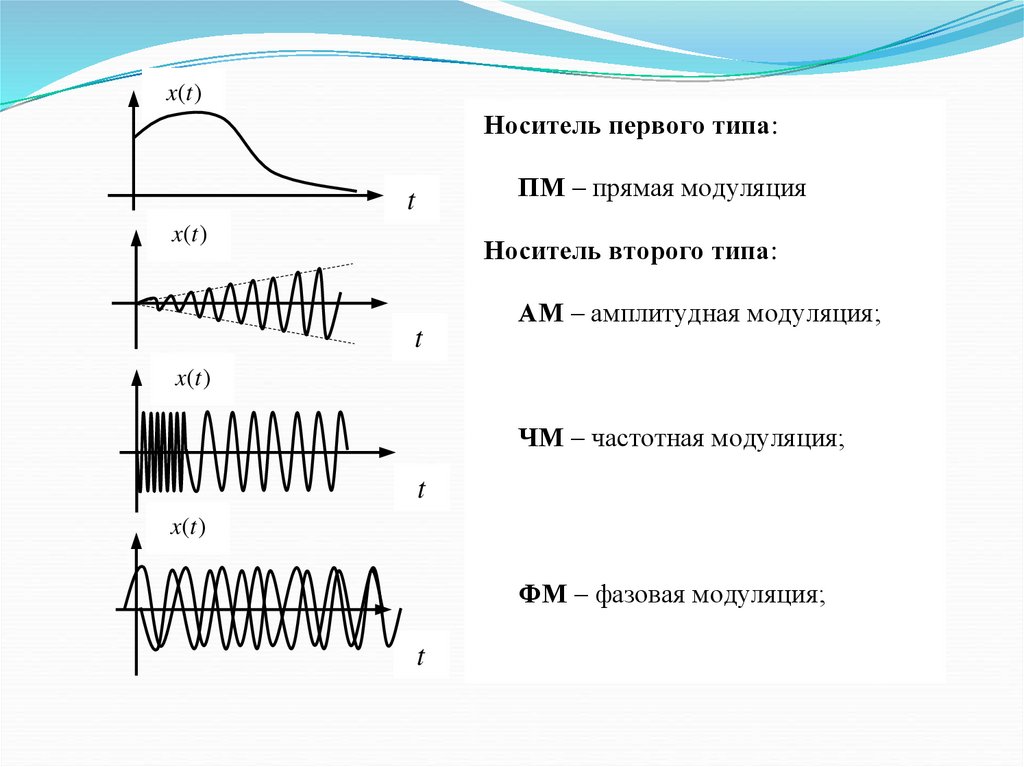
x(t )
Носитель первого типа:
ПМ – прямая модуляция
t
x(t )
Носитель второго типа:
t
АМ – амплитудная модуляция;
x(t )
ЧМ – частотная модуляция;
t
x(t )
ФМ – фазовая модуляция;
t
x(t )
Носитель третьего типа:

27.

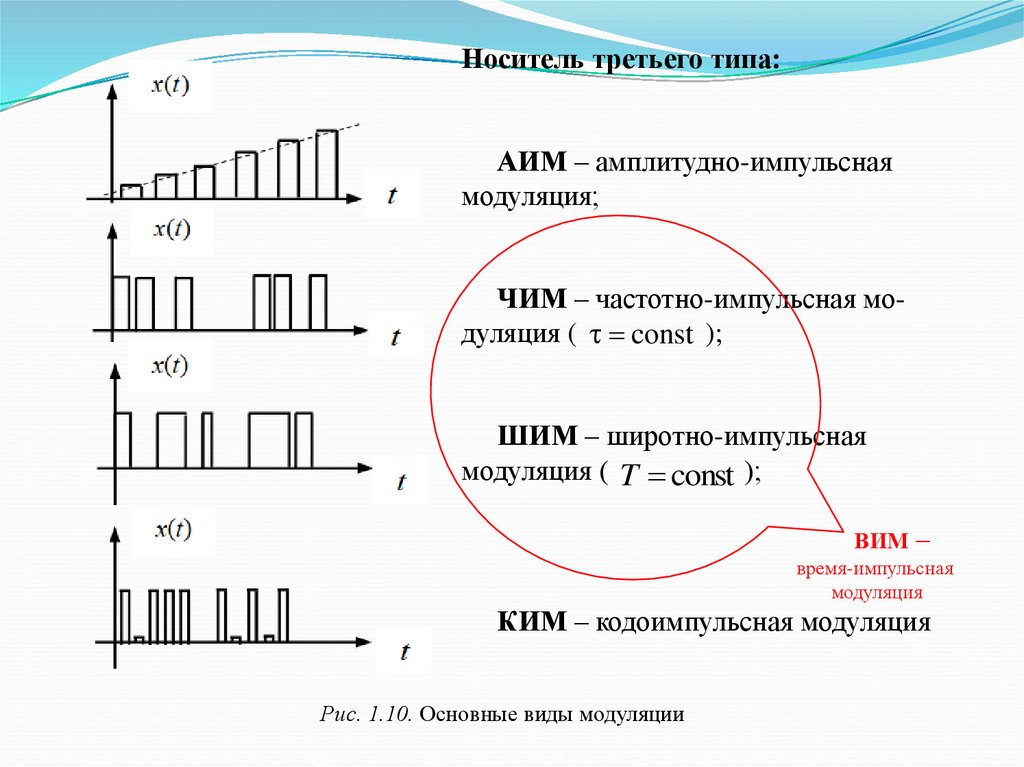
Носитель третьего типа:
АИМ – амплитудно-импульсная
модуляция;
ЧИМ – частотно-импульсная модуляция ( const );
ШИМ – широтно-импульсная
модуляция ( T const );
ВИМ –
время-импульсная
модуляция
КИМ – кодоимпульсная модуляция
Рис. 1.10. Основные виды модуляции

28.

Различные области профессиональной деятельности передачи
сигналов используют более сложные комбинированные виды
модуляции:
1. Квадратурная амплитудная модуляция (QAM).
2. Дифференциальная фазовая модуляция (DPM).
3. Треугольная модуляция (TM).
4. Бинарная амплитудная модуляция (BAM).
5. Аналогово-цифровая модуляция (ACM).
6. Широкополосная модуляция (WFM).
7. Цифровая фазовая модуляция (DPM).
8. Ортогональная многопозиционная модуляция
(QAM-Orthogonal).
Выбор конкретного типа модуляции зависит от требований к
передаче информации, условий канала связи и других факторов.
Каждый из этих типов модуляции имеет свои преимущества и
недостатки, и он может быть оптимальным в разных ситуациях.