Similar presentations:
Векторные и спектральные модели сигналов в инфотелекоммуникации
1. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических
Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-БруевичаКафедра «Теоретических основ связи и радиотехники»
Факультет фундаментальной подготовки
Кафедра теоретических основ связи и радиотехники
(ТОС и Р)
располагается на 6-м этаже
В аудиториях №607, №609, №611, 613.
Дисциплина
Общая теория связи
Лектор:
Заведующий кафедрой ТОС и Р
Шумаков Павел Петрович
Общая теория связи
Лекция №3
1
2. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических
Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-БруевичаКафедра «Теоретических основ связи и радиотехники»
Лекция № 3
Векторные и спектральные модели сигналов в
инфотелекоммуникации
1.
2.
3.
4.
Учебные вопросы:
Векторные модели сигналов. Обобщенный ряд Фурье.
Спектры периодических сигналов.
Спектры непериодических сигналов.
Теоремы о спектрах.
Общая теория связи
Лекция №3
2
3. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических
Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-БруевичаКафедра «Теоретических основ связи и радиотехники»
Литература:
Стр. 28..37; 37..40; 40..52
Используя MathCAD рассчитать и построить
энергетические спектры для импульсных
сигналов из таблицы 2.1 на стр. 45.
Четные номера : треугольный (2) и
косинусоидальный (3).
Нечетные номера : Прямоугольный (1) и SINCобразный (5).
Используя MathCAD рассчитать и построить
энергетические спектры для импульсных
сигналов вида:
Четные номера : пилообразный
возрастающий.
Нечетные номера : пилообразный
ниспдающий.
Общая теория связи
Лекция №3
3
4. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических
Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-БруевичаКафедра «Теоретических основ связи и радиотехники»
Задание на самостоятельную отработку
Теория электрической связи: учебное пособие для студентов высших учебных заведений
/Биккенин Р. Р., Чесноков М. Н. –М.: Издательский центр «Академия», 2010.
-28-37;37-40;40-52 с.
Общая теория связи
Лекция №3
4
5. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических
Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-БруевичаКафедра «Теоретических основ связи и радиотехники»
Импульсные сигналы:
а) видеоимпульсы;
б) радиоимпульсы
Uр(t) = Uв(t)cos(ωt + φ)
Uв(t) — огибающая радиоимпульса
ω — опорная (несущая) частота
φ — фаза
Общая теория связи
Лекция №3
5
6. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических
Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-БруевичаКафедра «Теоретических основ связи и радиотехники»
Вопрос №1. Векторное представление сигнала. Понятие базиса, нормы,
скалярного
произведения
сигналов,
ортогональности
сигналов, ортонормированного базиса сигналов.
Сигналы могут быть одномерными U1(t), и многомерными {UN(t)},
Многомерный (векторный) - сигнал образованный упорядоченным
множеством одномерных сигналов V(t) =
{U1(t),U2(t),…,UN(t)},
N — размерность сигнала.
Общая теория связи
Лекция №3
6
7. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических
Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-БруевичаКафедра «Теоретических основ связи и радиотехники»
Пространство сигналов
Множество сигналов М={s1(t), s2(t),…sn(t)} обладающих определенными свойствами
называется пространством сигналов. Структура пространства сигналов определяется
алгебраическими иАлгебраическая
геометрическимиструктура
свойствами.
пространства сигналов
Множество сигналов образует ВЕЩЕСТВЕННОЕ ЛИНЕЙНОЕ ПРОСТРАНСТВО СИГНАЛОВ L
если справедливы следующие аксиомы:
1.Все сигналы при любом времени t принимают только вещественные значения.
2.Сумма любого числа сигналов данного множества также принадлежит этому
множеству, при чем эта сумма подчиняется свойствам: для
x =Si(t)
y = Sj(t)
x + y = y + x — коммутативность;
x + (y + z) = (x + y )+ z — ассоциативность;
x + = x , где — нулевой элемент;
x + (- x) = 0 , где -x — противоположный элемент.
3. Умножение сигнала на скаляр (число) определяет новый сигнал принадлежащий
исходному множеству si(t) М.
4. Операция умножения на скаляр подчиняется свойствам:
(bx)= ( b)x
1x= x
( +b)x)= x+bx
(x+y)= x+ y
Общая теория связи
Лекция №3
7
8.
• Еслибудет
произвольным
комплексным числом, то множество
сигналов образует
• Комплексное Линейное Пространство
Сигналов С.
• Элементы
структурированного
пространства в математике называются
точками, функциями, векторами.
Общая теория связи
Лекция №3
8
9. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических
Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-БруевичаКафедра «Теоретических основ связи и радиотехники»
Геометрическая структура пространства сигналов
Норма сигнала .
Эквивалентом длины вектора для аналоговых и дискретных сигналов является норма
Для вещественного сигнала норма определяется :
s( t )
2
s
( t )dt
T
Для комплексного сигнала норма определяется :
s( t )
Норма подчиняется следующим аксиомам:
s( t ) 0
s( t ) s( t )
s(
t
)s
( t )dt
T
s1 ( t ) s2 ( t ) s1 ( t ) s2 ( t )
Если S — это вектор, то норма – это его длина или расстояние от конца вектора до начала
координат.
Энергия сигнала
Пусть s(t) ― напряжение на резисторе с сопротивлением в 1 Ом, тогда s2(t) ―
мгновенная мощность, а квадрат нормы ― есть энергия, выделяемая на резисторе за время
T.
s( t ) s 2 ( t )dt E s
2
Общая теория связи
T
Лекция №3
9
10. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических
.Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича
Кафедра «Теоретических основ связи и радиотехники»
Геометрическая структура пространства сигналов
Метрика пространства сигналов
Для усовершенствовании структуры пространства вводится расстояние между его
элементами, которое называют также метрикой.
Каждой паре элементов пространства ставится в соответствие положительное число,
которое трактуется как расстояние между элементами. В качестве расстояния используется
функционал
свойствами:
d(x,y) = R,
называемый
метрикой
и обладающий следующими
d(x,y) ≥ 0 и d(x,y) = 0, только если x = y;
d(x,y) = d(y,x) – cвойство симметрии;
d(x,y) < d(x,z) + d(z,y) – неравенство треугольника.
В качестве метрики можно выбрать величину
d ( x, y ) x y
Линейное метрическое пространство с квадратичной нормой обозначается:
Вещественное
Общая теория связи
L2
комплексное
Лекция №3
С2
10
11. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических
Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-БруевичаКафедра «Теоретических основ связи и радиотехники»
Геометрическая структура пространства сигналов
Скалярное произведение сигналов
Найдем энергию суммы двух сигналов u(t) и v(t).
u( t ) v( t ) u( t )2 dt v( t )2 dt 2 u( t )v ( t )dt
2
T
T
T
Если сигналы рассматривать как вектора U и V получим
U V U V 2 U V cos( )
2
Где
2
2
(U ,V ) U V cos( )
UV
скалярное произведение двух векторов
угол между векторами
Сопоставляя сигналы с векторами в пространстве L2 получим что скалярное
произведение двух сигналов
( u( t ),v( t )) u( t )v ( t )dt u( t ) v( t ) cos( )
T
Общая теория связи
Лекция №3
11
12. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических
Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-БруевичаКафедра «Теоретических основ связи и радиотехники»
Свойства скалярного произведения сигналов
Для комплексных сигналов скалярное произведение должно удовлетворять следующим
условиям:
(x, y) = (y, x)* , где знак * означает комплексно сопряженную величину;
(αx, y) = α(x, y);
(x1 + x2, y) = (x1, y) + (x2, y);
(x, x) ≥ 0.
Ортогональность двух сигналов
Если
UV 90
cos(
2
[градусов]
UV 2
[радиан]
) 0
то скалярное произведение двух сигналов равно нулю , значит взаимная энергия этих
сигналов равна нулю , а такие сигналы - ортогональные.
Общая теория связи
Лекция №3
12
13.
ЕслиS2(t) = 0
то имеем систему передачи с пассивной паузой
S1(t) = Uc sin ( 0t + ),
t 0,T ,
S1(t) = 0
T
1
( S0 , S1 ) S0 (t ) S1 (t )dt 0
T0
T
d 2 ( S0 (t ), S1 (t )) S0 2 (t )dt E1
0
Общая теория связи
Лекция №3
13
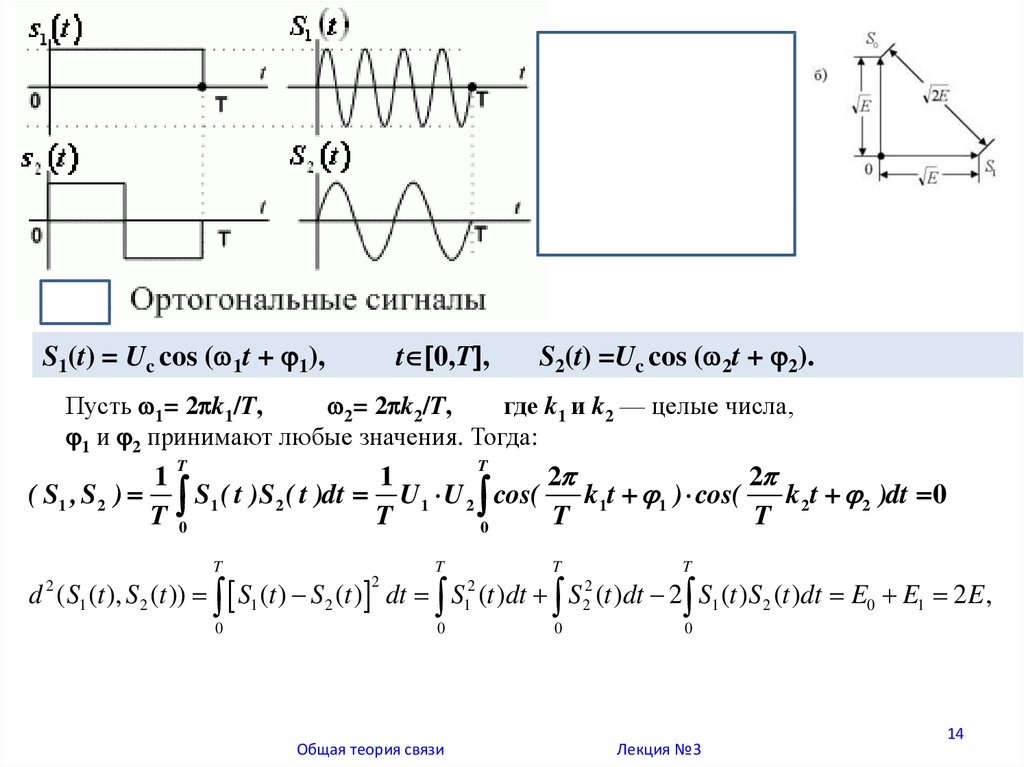
14.
S1(t) = Uc cos ( 1t + 1),t 0,T ,
S2(t) =Uc cos ( 2t + 2).
Пусть 1= 2 k1/T,
2= 2 k2/T,
где k1 и k2 — целые числа,
1 и 2 принимают любые значения. Тогда:
1
1
2
2
( S1 , S2 ) S1 ( t )S 2 ( t )dt U 1 U 2 cos(
k1t 1 ) cos(
k 2t 2 )dt 0
T 0
T
T
T
0
T
T
T
T
T
T
d ( S1 (t ), S2 (t )) S1 (t ) S2 (t ) dt S (t )dt S (t )dt 2 S1 (t )S 2 (t )dt E0 E1 2 E ,
2
2
0
2
1
0
Общая теория связи
2
2
0
0
Лекция №3
14
15. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических
Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-БруевичаКафедра «Теоретических основ связи и радиотехники»
В линейном пространстве сигналов
определить совокупность линейно
Базисныеможно
сигналы
независимых сигналов {ei(t)} таких, что весовая сумма iei=0 возможна только при
одновременном равенстве нулю всех коэффициентов . Эти сигналы называются
координатным базисом. Базисные сигналы попарно ортогональные.
Обобщенный ряд Фурье
Если выбраны сигналы координатного базиса, то любой сигнал s(t) в линейном
пространстве может быть представлен взвешенной суммой ортогональных сигналов
координатного базиса
Сiei(t)=s(t)
Такое представление сигнала называется обобщенный ряд Фурье.
Французский математик Жан Батист Жозеф Фурье (1768-1830)
Весовые коэффициенты этого ряда рассчитываются как скалярное
произведение сигнала s(t) и соответствующего i- того базисного сигнала ei(t):
Ci ( s( t ),ei ( t ))
1
ei
2
s(
t
)e
i ( t )dt s( t ) ei ( t ) cos( ) s( t ) cos( )
T
Совокупность коэффициентов обобщенного ряда Фурье {Сi}
сигнала s(t) в базисе ортогональных сигналов {ei(t)}
Общая теория связи
Лекция №3
называется спектром
15
16. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических
Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-БруевичаКафедра «Теоретических основ связи и радиотехники»
Выводы по первому вопросу
1.Сигналы в радиотехнике рассматриваются как проявления электромагнитного
поля в элементах радиотехнических цепей в виде колебаний напряжения или тока.
2.Обобщенной математической моделью сигналов является их описание как
элементов функционального пространства (векторов ).
3.Вещественные и комплексные сигналы можно рассматривать как элементы
множества векторного линейного нормированного метрического пространства.
4.Скалярное произведение двух сигналов по физическому смыслу представляет
собой взаимную энергию между двумя сигналами , действующими суммарно на
сопротивление в один Ом.
5.Скалярное произведение двух сигналов определяется углом между ними. Если
угол между двумя сигналами равен 90 градусов то скалярное произведение равно
нулю, и такие сигналы являются ортогональными.
6. Набор ортогональных сигналов называется координатным базисом
пространства сигналов.
7. При известном базисе , любой сигнал можно представить взвешенной суммой
сигналов ортогонального базиса в виде обобщенного ряда Фурье. Весовые
коэффициенты этого ряда называются спектром сигнала.
Общая теория связи
Лекция №3
16
17. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических
Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-БруевичаКафедра «Теоретических основ связи и радиотехники»
Вопрос 2. Спектры периодических сигналов.
Периодическим называют сигнал, мгновенные значения которого повторяются через
равные промежутки времени – Т
Модель такого сигнала имеет вид
где Т- период повторения, а F=1/T-частота повторения периодического сигнала (ПС)
Основной математический аппарат спектрального анализа таких сигналов –ряд Фурье в
базисе гармонических сигналов с кратными частотами.
s t s t k T ,
Формы спектрального представления периодического сигнала
Квадратурная
a0
2
2
s( t k T ) sT ( t ) ak cos(
kt ) bk sin(
kt )
2 k 1
T
T
T / 2
2
2
ak
S(
t
)cos(
kt )dt
амплитуда синфазных гармоник
T T / 2
T
периодического сигнала
T / 2
2
2
bk
S( t ) sin( kt )dt амплитуда квадратурных гармоник
T T / 2
T
периодического сигнала
T / 2
2
a0
S( t )dt
T T / 2
постоянная составляющая
периодического сигнала
Общая теория связи
Лекция №3
17
18. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических
Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-БруевичаКафедра «Теоретических основ связи и радиотехники»
Амплитудно – фазовая форма ряда Фурье
a0
sT ( t ) s( t k T ) Ak cos( xk k )
2 k 1
ak cos xk bk sin xk ak 2 bk 2 cos( xk k )
2
xk
kt k 2 f1t k 1t k t;
T
2
2
ak bk Ak амплитудно-частотный спектр (АЧС)
bk
фазочастотный спектр (ФЧС)
k arctg
ak
ak Ak cos( k )
bk Ak sin( k )
Общая теория связи
Лекция №3
18
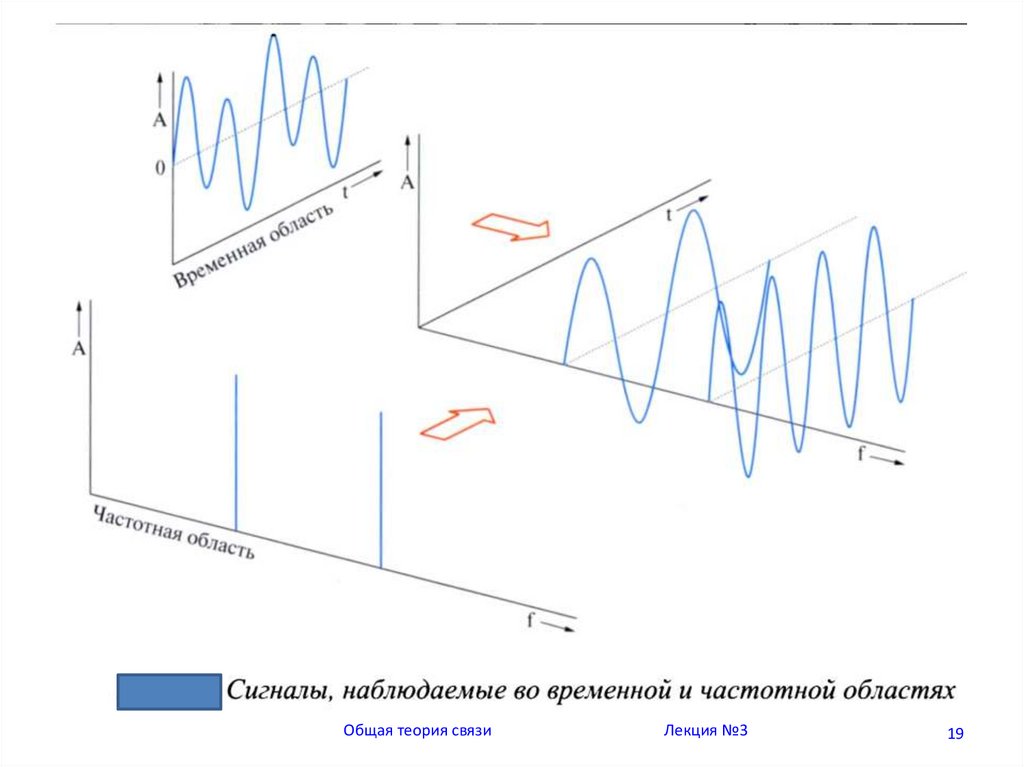
19.
Общая теория связиЛекция №3
19
20. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических
Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-БруевичаКафедра «Теоретических основ связи и радиотехники»
Комплексная форма ряда Фурье
e jx e jx
cos x
2
a0 a k
s( t k T )
2 k 1 2
e jx e jx
sin x
j2
2
2
2
j
t
j
t
j
t
j 2T t
b
k
T
e T
e T
e
e
j2
2
2
j
t
j
t
a0 1
1
T
T
ak jbk e
ak jbk e
2 k 1 2
k 1 2
2
2
2
j
kt
j
kt
j
kt
a0 1
1
j k
j k
T
T
T
s( t k T ) Ak e e
Ak e e
Ck e
2 k 1 2
k 1 2
k
Общая теория связи
Лекция №3
20
21. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических
Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-БруевичаКафедра «Теоретических основ связи и радиотехники»
Комплексная форма ряда Фурье
Ak j k 1
Ck
e
2
T
T / 2
S( t )e
j
2
kt
T
dt
T / 2
Ak ak jbk , A k ak jbk
1
1
ak
Ak A k
bk j Ak A k
2
2
Ak
Ck
амплитудно-частотный спектр (АЧС)
Модуль
2
фазочастотный спектр (ФЧС)
Аргумент k arg C k
АЧС –четная функция частоты (обладает симметрией в области
положительных и отрицательных частот)
ФЧС – нечетная функция (обладает центральной симметрией)
Общая теория связи
Лекция №3
21
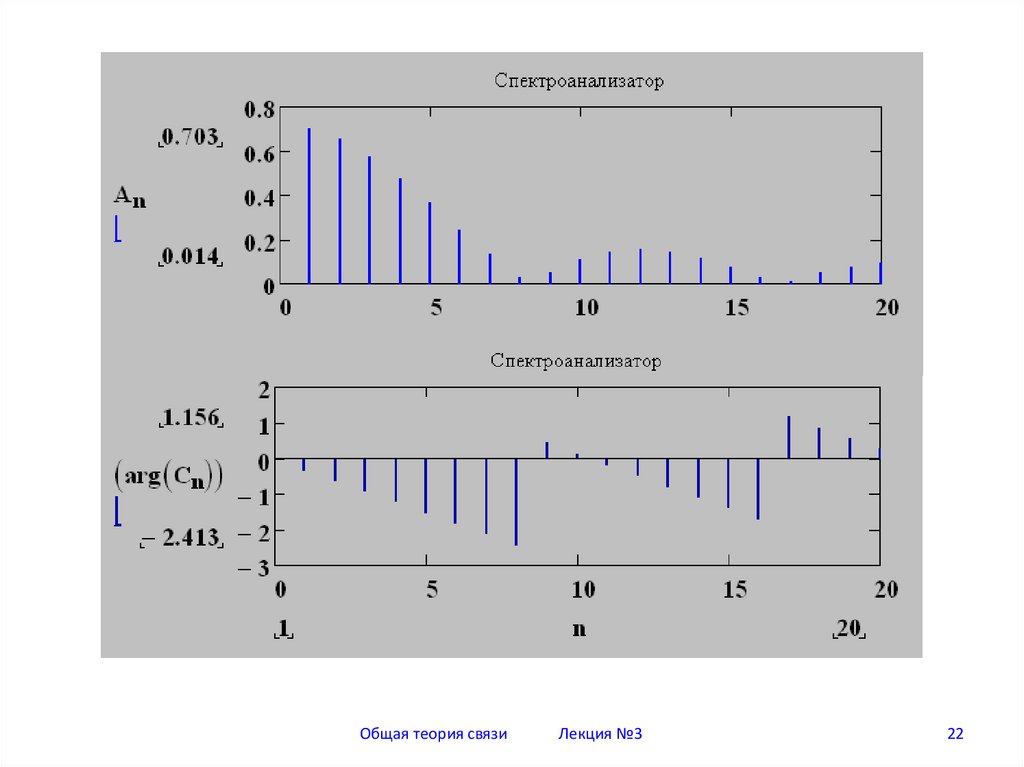
22.
Общая теория связиЛекция №3
22
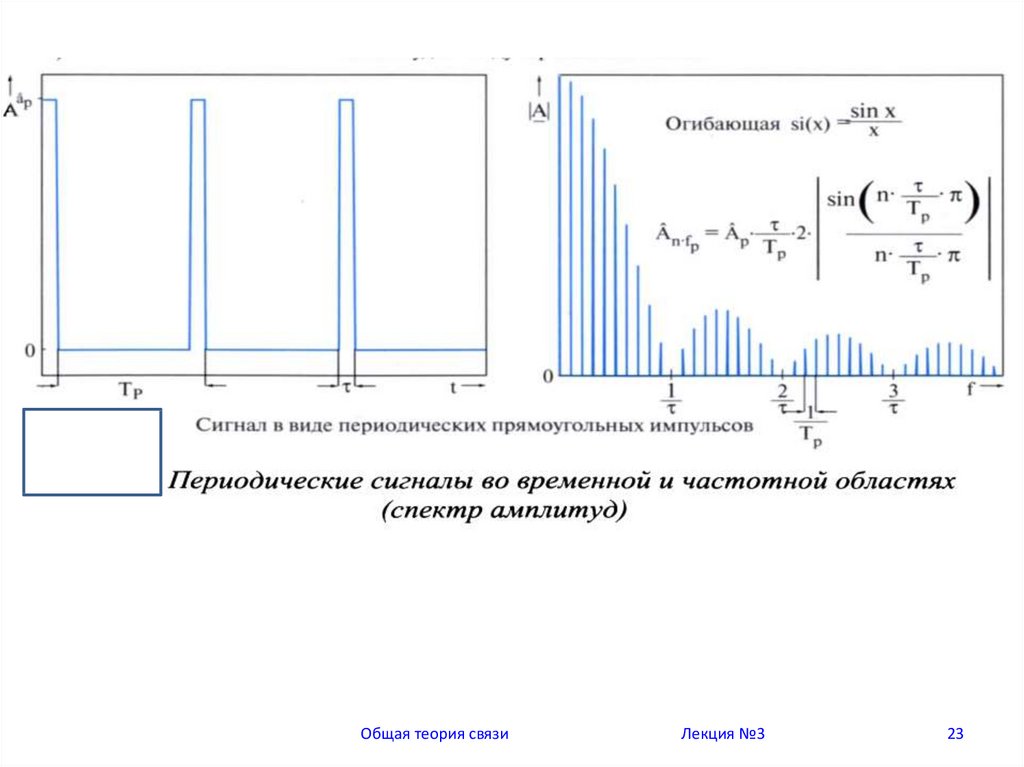
23.
Общая теория связиЛекция №3
23
24. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических
Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-БруевичаКафедра «Теоретических основ связи и радиотехники»
Вопрос 3. Спектры непериодических сигналов.
В подавляющем большинстве случаев в теории и технике связи приходится иметь дело с
сигналами, которые по существу являются непериодическими. К таким сигналам аппарат
рядов Фурье не применим.
Модель непериодического сигнала как предельного случая периодического сигнала ,
когда период стремится к бесконечности
Устремим в периодическом сигнале T
1
s (t )
2
k
или
f1 = 1/T = 1/2 0
Ak Te jk 1t
где = 1 = k 1 – (k – 1) 1 — разность между частотами соседних гармоник
S( j ) lim AkT lim
T
0
Ak
Общая теория связи
2
спектральная плотность непериодических
сигналов
Лекция №3
24
25. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических
Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-БруевичаКафедра «Теоретических основ связи и радиотехники»
Вопрос 3. Спектры непериодических сигналов.
В подавляющем большинстве случаев в теории и технике связи приходится иметь дело с
сигналами, которые по существу являются непериодическими. К таким сигналам аппарат
рядов Фурье не применим.
Модель непериодического сигнала как предельного случая периодического сигнала ,
когда период стремится к бесконечности
Устремим в периодическом сигнале T
1
s (t )
2
k
или
f1 = 1/T = 1/2 0
Ak Te jk 1t
где = 1 = k 1 – (k – 1) 1 — разность между частотами соседних гармоник
S( j ) lim AkT lim
T
0
Ak
Общая теория связи
2
спектральная плотность непериодических
сигналов
Лекция №3
25
26. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических
Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-БруевичаКафедра «Теоретических основ связи и радиотехники»
Прямое и обратное преобразование Фурье
1
s (t )
2
S ( j )
j t
S ( j )e d -
прямое преобразование Фурье (ППФ)
s(t )
s(t )e j t dt -
S ( j )
обратное преобразование Фурье (ОПФ)
Обратное преобразование Фурье для сигнала s(t) - операция синтеза, поскольку с ее
помощью сигнал восстанавливается (синтезируется) из спектральных
составляющих.
Прямое преобразование Фурье – операция анализа сигнала на основе определения его
спектральных составляющих.
Общая теория связи
Лекция №3
26
27. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических
Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-БруевичаКафедра «Теоретических основ связи и радиотехники»
Физический смысл спектральной плотности сигнала
Учитывая чётность модуля S(ω) и нечётность фазы φ(ω), обратное преобразование
Фурье можно записать следующим образом
s (t )
1
S ( j ) cos[ t ( )]d
0
1
j t
S ( j )d e
2
1 Am
S ( j )
c d
1
S ( )d cos[ t ( )]
1
c
Спектральная плотность сигнала является комплексной амплитудой эквивалентной
гармоники на соответствующей опорной частоте .
Эквивалентная гармоника есть результат когерентного сложения бесконечно большого
числа гармоник с бесконечно малыми амплитудами расположенными в бесконечно малом
по частоте диапазоне в районе выбранной (опорной) частоты.
Общая теория связи
Лекция №3
27
28. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических
Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-БруевичаКафедра «Теоретических основ связи и радиотехники»
Вопрос 4. Свойства преобразования Фурье
№
Название теоремы
Временное представление
Спектральное представление
п/п
1
Теорема сложения
2
Теорема временного сдвига
S1 (t ) S (t t0 )
S1 ( j ) S ( j )e
3
Теорема смещения (модуляции)
S1 (t ) S (t )e j 0t
S1 ( j ) S ( j( 0 ))
4
Теорема об изменении масштаба
t
S1 (t ) S
a
S1 ( j ) aS ( ja )
5
Теорема о дифференцировании
dS (t )
dt
S1 ( j ) j S ( j )
6
Теорема об интегрировании
t
1
S1 ( j )
S ( j )
j
S ( j ) S1 ( j ) S2 ( j )
S (t ) S1 (t ) S2 (t )
S1 (t )
S1 (t )
S (t )dt
7
Теорема о свёртке
S (t )
S ( j ) S1 ( j )S2 ( j )
S ( )S (t )d S (t )* S (t )
1
2
1
j t0
2
8
Преобразование Фурье
S1 (t )
1
2
S ( j )e
j t
d
S ( j )
S (t )e
j t
dt
Общая теория связи
Лекция №3
28
29. Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических
Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-БруевичаКафедра «Теоретических основ связи и радиотехники»
Вопрос 4. Свойства преобразования Фурье
Теорема сложения спектров гласит: спектр суммы колебаний равен
сумме спектров слагаемых колебаний.
Теорема временного сдвига (запаздывания) формулируется
следующим образом: при сдвиге колебания во времени (изменении
начального момента отсчёта времени) спектральная плотность амплитуд
сохраняется постоянной, а спектр фаз изменяется на величину,
пропорциональную частоте и времени сдвига с учётом его знака.
j 0t
Теорема смещения (модуляции): умножение колебания S(t) на
приводит к смещению его спектра на величину ω0.
Теорема об изменении масштаба: растяжение колебания во времени
(a>1) влечёт за собой сжатие его частотного спектра и увеличение
спектральной плотности амплитуд. Сжатие колебания во времени (a<1)
приводит к расширению его частотного спектра и уменьшению
спектральной плотности амплитуд.
Теорема о свёртке: свёртка двух колебаний S1(t) и S2(t) соответствует
перемножению их спектров.
e
Общая теория связи
Лекция №3

























 electronics
electronics








