3_1 Ан_Геом_Пространство24

1.

Раздел 7. АНАЛИТИЧЕСКАЯ
ГЕОМЕТРИЯ НА ПЛОСКОСТИ И
В ПРОСТРАНСТВЕ
Аналитическая геометрия – это раздел математики, в
котором свойства геометрических объектов изучаются
алгебраическими методами. При этом геометрические объекты
описываются уравнениями и изучение их свойств сводится к
исследованию уравнений.
В аналитической геометрии рассматриваются два типа
задач.
1. Составить уравнение геометрического объекта по
известным свойствам этого объекта.
2. По данному уравнению
определить его свойства.
геометрического
объекта

2.

В стереометрии любую пространственную фигуру можно
рассматривать как геометрическое место точек (г.м.т.), т.е.
как множество точек, каждая из которых удовлетворяет
заданному характеристическому свойству (точка, не
принадлежащая этому множеству, не удовлетворяет этому
свойству).
В
аналитической
геометрии
пространственные
геометрические фигуры задаются как множества решений
соответствующих уравнений. Рассмотрим, например,
уравнение F(x,y,z)=0 с тремя неизвестными x,y,z.
Его решением называется тройка чисел, при подстановке
которых вместо неизвестных уравнение превращается в
верное числовое равенство. Каждое решение x,y,z уравнения
F(x,y,z)=0 можно рассматривать как точку M(x,y,z) в
координатном пространстве с абсциссой x ординатой y и
аппликатой z.

3.

Таким образом, множество F точек M(x,y,z) координаты
которых удовлетворяют уравнению F(x,y,z)=0, образуют в
координатном пространстве некоторую фигуру
F M x; y; z : F x; y; z 0
Уравнением поверхности в декартовой системе координат
Oxyz называется уравнение с тремя переменными F(x,y,z) = 0,
которому удовлетворяют координаты любой точки, лежащей на
этой поверхности, и не удовлетворяют координаты точек, не
лежащих на ней. Входящие в уравнение F(x,y,z) = 0 координаты
(x,y,z) произвольной точки поверхности называются текущими
координатами.
Простейшей поверхностью в пространстве является плоскость.
Уравнения плоскости впервые встречается у А. К. Клеро (1731).
Уравнение плоскости в отрезках, по-видимому, впервые
встречается у Г. Ламе (1816—1818).
Нормальное уравнение ввёл Л. О. Гессе (1861).

4.

Клеро родился в семье парижского
Алекси́ Клод Клеро́ (фр. Alexis
преподавателя математики. Уже в
Claude Clairaut или фр. Clairault, возрасте двенадцати лет он поразил
7 мая 1713, Париж — 17 мая
парижских академиков своей
1765) — французский математик, работой о некоторых кривых
механик и астроном.
четвёртого порядка, и они устроили
Клеро целый экзамен, чтобы
убедиться в его авторстве. Экзамен
Клеро выдержал.
В 1729 году 16-летний Клеро
представил той же академии новый
трактат: «Исследования о кривых
двоякой кривизны». Эта книга
положила начало сразу трём
геометрическим дисциплинам:
аналитической геометрии в
пространстве (Декарт занимался
плоскими кривыми),
дифференциальной геометрии и
начертательной геометрии.

5.

§ 1. Плоскость в пространстве.
Различные виды уравнения
плоскости
Плоскость в пространстве однозначно задается:
- тремя точками, лежащими в этой плоскости;
- вектором, перпендикулярным плоскости, и точкой,
лежащей в этой плоскости.

6.

Уравнение плоскости, проходящей через три заданные
точки M1(x1; y1; z1), M2(x2; y2; z2), M3(x3; y3; z3)
Пусть M(x; y; z) – произвольная точка
этой плоскости.
Точки M1, M2, M3 лежат в одной
плоскости тогда и только тогда,
когда векторы
M1M {x x1; y y1; z z1};
M
M1
M3
M2
M1M 2 {x2 x1; y2 y1; z2 z1};
M1M 3 {x3 x1; y3 y1; z3 z1}.
компланарны, т. е. их смешанное произведение равно 0.
x x1
x2 x1
x3 x1
y y1
y2 y1
y3 y1
z z1
z2 z1 0.
z3 z1
(1)

7.

Пример 1. Напишем уравнение плоскости, проходящей через
точки M1(1; 2; 3), M2(2; –7; 0), M3(4; 3; –2).
x 1 y 2
z 3
2 1 7 2 0 3 0;
4 1 3 2 2 3
x 1 y 2 z 3
1
9
3 0.
3
1
5
9 3
1 3
1 9
( x 1)
( y 2)
( z 3)
0;
1 5
3 5
3 1
48( x 1) 4( y 2) 28( z 3) 0;
48x 4 y 28z 124 0.
12 x y 7 z 31 0.

8.

Уравнение плоскости, проходящей через данную точку
M0(x0; y0; z0) перпендикулярно заданному вектору n { A; B; C}
Опр. 1. Вектор, перпендикулярный к плоскости, называется
вектором нормали к этой плоскости, или нормальным
вектором плоскости.
Замечание. Вектор нормали к плоскости определяется неоднозначно. Если
n { A; B; C} – нормальный вектор плоскости, то любой ненулевой вектор,
коллинеарный данному, также является вектором нормали к этой плоскости.
n
M0
Пусть плоскость имеет нормальный вектор
n { A; B; C}и проходит через точку M0(x0; y0; z0).
Пусть M(x; y; z) – произвольная точка этой
M
плоскости.
n { A; B; C} и M 0 M {x x0 ; y y0 ; z z0 } ортогональны.
n M 0 M 0.
A( x x0 ) B( y y0 ) C ( z z0 ) 0.
(2)

9.

Общее уравнение плоскости
A( x x0 ) B( y y0 ) C ( z z0 ) 0.
Ax By Cz Ax0 By0 Cz0 0.
D ( Ax0 By0 Cz0 ).
Тогда получим общее уравнение плоскости
Ax By Cz D 0,
(3)
причем коэффициенты A, B, C являются координатами вектора
нормали к этой плоскости: n { A; B; C}.
Тh 1. Пусть в трехмерном пространстве задана система
координат Oxyz. Тогда всякое уравнение вида (3), т. е. линейное
уравнение (уравнение 1-й степени) относительно переменных x,
y, z, в котором хотя бы один из коэффициентов A, B, C не равен
нулю, задает некоторую плоскость в пространстве. И обратно,
любая плоскость в пространстве может быть задана уравнением
вида (3).

10.

Исследование общего уравнения плоскости
1. Если A = 0, то уравнение примет вид By + Cz + D = 0.
Нормальный вектор n 0; B; C перпендикулярен оси Ox.
Следовательно, плоскость параллельна оси Ox.
Аналогично, при B = 0 плоскость Ax + Cz + D = 0 параллельна
оси Oy.
Если C = 0, то плоскость Ax + By + D = 0 параллельна оси Oz.
2. Если D = 0, то Ax + By + Cz = 0. Этому уравнению
удовлетворяет точка O(0; 0; 0). Следовательно, в данном случае
плоскость проходит через начало координат.
3. Если A = D = 0, т. е. уравнение имеет вид By + Cz = 0, то
плоскость проходит через O(0; 0; 0) параллельно оси Ox, т. е.
By + Cz = 0 проходит через ось Ox.
При B = D = 0 плоскость Ax + Cz = 0 проходит через ось Oy.
При C = D = 0 плоскость Ax + By = 0 проходит через ось Oz.

11.

4. Если A = B = 0, то Cz + D = 0.
Плоскость ┴ оси Oz ( || плоскости Oxy)
(вектор n {0;0; C} || плоскости Oxy).
При A = C = 0 плоскость By + D = 0 ┴ оси Oy ( || плоскости Oxz).
При B = C = 0, то плоскость Ax + D = 0 ┴ оси Ox ( || плоскости Oyz).
5. Если A = B = D = 0, то уравнение примет вид Cz = 0, или z = 0.
Эта плоскость совпадает с плоскостью Oxy.
При A = C = D = 0 получим By = 0, или y = 0 – плоскость Oxz.
Если B = C = D = 0, то Ax = 0, т. е. x = 0 – плоскость Oyz.

12.

Если в уравнении Ax+By+Cz+D = 0 все коэффициенты A,B,C
и D отличны от нуля, то уравнение называют полным; если
хотя бы один из коэффициентов равен нулю – неполным.
Пусть общее уравнение плоскости – полное. Тогда его
можно записать в виде Ax By Cz D,
x
y
z
1,
D
D
D
A
B
C
D
D
D
c
b
a
Приняты обозначения:
C
B
A
x y z
1
a b c
С геометрической точки зрения a ,
b и c – отрезки, отсекаемые
плоскостью на координатных осях
Ox, Oy и Oz соответственно.
Уравнение называют уравнением
плоскости в отрезках.

13.

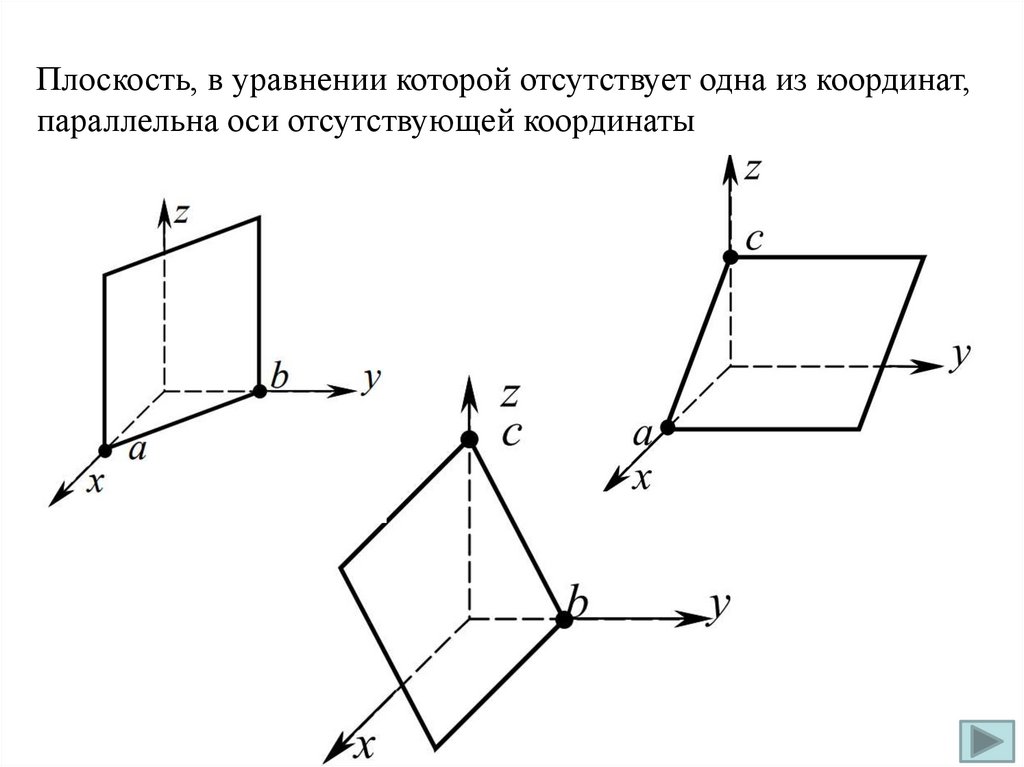
Плоскость, в уравнении которой отсутствует одна из координат,
параллельна оси отсутствующей координаты

14.

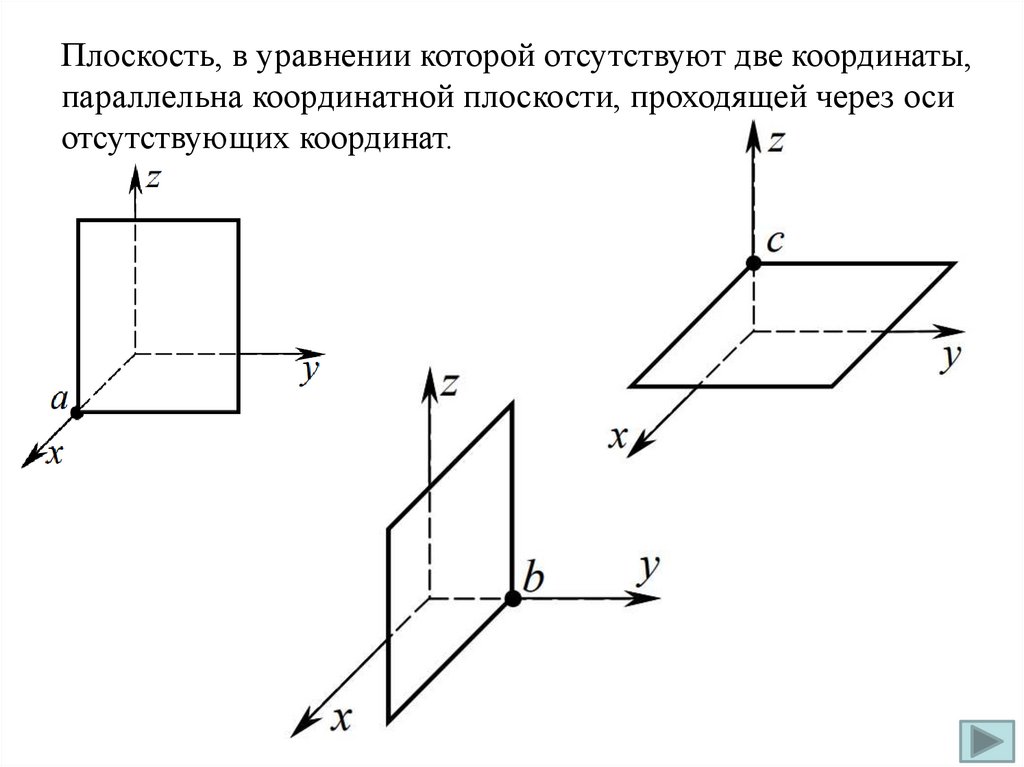
Плоскость, в уравнении которой отсутствуют две координаты,
параллельна координатной плоскости, проходящей через оси
отсутствующих координат.

15.

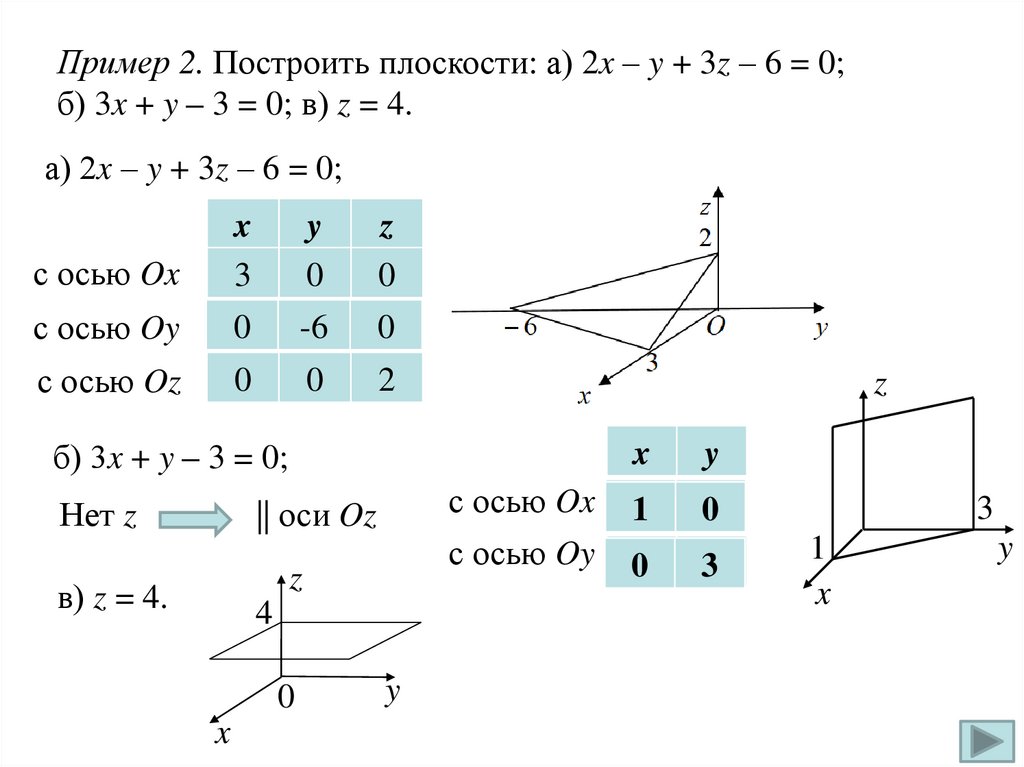
Пример 2. Построить плоскости: а) 2x – y + 3z – 6 = 0;
б) 3x + y – 3 = 0; в) z = 4.
а) 2x – y + 3z – 6 = 0;
с осью Oy
x
3
0
с осью Oz
0
с осью Ox
y
0
-6
0
z
0
0
2
z
б) 3x + y – 3 = 0;
Нет z
|| оси Oz
z
в) z = 4.
4
0
x
y
x
y
с осью Ox
1
0
с осью Oy
0
3
3
1
x
y

16.

Пусть заданы точки М1(x1, y1, z1), M2(x2, y2, z2) и вектор
a (m, n, p)
Составим уравнение плоскости, проходящей через данные
точки М1 и М2 и произвольную точку М(х, у, z) параллельно
вектору a
Векторы M1M {x x1; y y1; z z1};
M1M 2 {x2 x1; y2 y1; z2 z1};
и вектор a (m, n, p )
должны быть компланарны, т.е. M 1M M 1M 2 a 0
Уравнение плоскости:
x x1 y y1
x2 x1
m
y2 y1
n
z z1
z2 z1 0
p

17.

Пусть заданы два неколлинеарных вектора l (m , n , p )
1
1
1
1
и
l2 (m2 , n2 , p2 ) . Найдем уравнение плоскости, проходящей
через данную точку М0 (x0, y0, z0) параллельно векторам.
Тогда для произвольной точки М(х, у, z), принадлежащей
плоскости, векторы l1 , l2 , MM 0 должны быть компланарны.
Уравнение плоскости, проходящей через заданную точку и
компланарной двум неколлинеарным векторам::
x x0
m1
m2
y y0
n1
n2
z z0
p1 0
p2

18.

Пусть задана точка М0 (x0, y0, z0)
и два неколлинеарных вектора
l1 (m1 , n1 , p1 ) и l2 (m2 , n2 , p2 )
Требуется
составить
параметрические
уравнения
плоскости.
Выберем произвольную точку М(х, у, z).
радиус векторы точек М и М0 r OM r OM
0
Обозначим
0
Точка М(х, у, z),принадлежащей плоскости тогда и только тогда,
когда, векторы l1 , l2 , MM 0 компланарны.
M 0 M t1 l1 t2 l2 где t1 t2 некоторые действительные числа
(параметры).
Учитывая, что
M 0 M r r0

19.

Векторное параметрическое уравнение плоскости:
l1 , l2
r0
r r0 t1 l1 t2 l2 t1 , t2 R
— направляющие векторы плоскости,
— радиус-вектор точки, принадлежащей плоскости.
Кординатная форма записи уравнения называется
параметрическим уравнением плоскости:
x x0 t1m1 t2 m2
y y0 t1n1 t2 n2
t1 , t2 R
z z t p t p
0
1 1
2 2
Параметры t1 ,t2 в уравнениях имеют следующий геометрический
смысл: величины t1 ,t2 пропорциональны расстоянию от заданной
точки М0 (x0, y0, z0) до точки М(х, у, z), принадлежащей плоскости.
При t1 =t2 =0 точка М совпадает с заданной точкой М0
При возрастании t1 точка М перемещается в направлении вектора
l1 , а при убывании t1 — в противоположном направлении.

20.

Пусть плоскость λ не проходит через O(0;0;0)
Обозначим:
1) P0(x0,y0,z0) – основание
перпендикуляра, опущенного на
λ из начала координат,
2) n cos ,cos ,cos орт вектора
3) p OP0
OP0
– расстояние от начала координат до λ .
Тогда уравнение λ можно записать в виде
cos x cos y cos z p 0
Это нормальное уравнение плоскости.

21.

Взаимное расположение двух плоскостей
П1: A1x + B1y + C1z + D1 = 0;
П2: A2x + B2y + C2z + D2 = 0.
n1 A1; B1; C1 , n2 A2 ; B2 ; C2
Условие параллельности двух плоскостей.
A1 B1 C1
П1 П 2 n1 n2
.
A2 B2 C2
При этом если A1 B1 C1 D1 ,
A2 B2 C2 D2
то плоскости П1 и П2 совпадают.
Условие перпендикулярности двух
плоскостей.
n1 n2 0.
П1 П 2 n1 n2
A1A2 + B1B2 + C1C2 = 0.

22.

Угол между двумя плоскостями
Под углом между плоскостями П1 и П2 понимается один из
двугранных углов, образованных этими плоскостями.
cos
cos
n1 n2
n1 n2
,
A1 A2 B1B2 C1C2
A12 B12 C12 A22 B22 C22
.
Замечание. Для нахождения острого угла следует взять модуль
правой части.

23.

Расстояние от точки до плоскости
Утв. 1. Расстояние от точки M0(x0; y0; z0) до плоскости
M0
Ax + By + Cz + D = 0 вычисляется по формуле
d
Ax0 By0 Cz0 D
A B C
2
2
2
.
d
Доказательство.
d пр n M 1M 0
M1
M 1M 0 n
( x0 x1 ) A ( y0 y1 ) B ( z0 z1 )C
A B C
2
n
2
Ax0 By0 Cz0 Ax1 By1 Cz1
A B C
2
2
2
2
.
Т.к. точка M1(x1; y1; z1) принадлежит плоскости, то
Ax1 By1 Cz1 D 0, т. е. D Ax1 By1 Cz1.
d
Ax0 By0 Cz0 D
A B C
2
2
2
.
◄

24.

Пример. Даны точки М1 (-3; 7; -5) и М2 (-8; 3; -4). Составить
уравнение плоскости, проходящей через точку М1 и
перпендикулярной вектору N M 1M 2
Решение: Найдем координаты нормального вектора
N 5; 4;1
Уравнение плоскости A( x x0 ) B ( y y0 ) C ( z z0 ) 0
5( x 3) 4( y 7) ( z 5) 0
5 x 4 y z 18 0

25.

Пример. Через точку пересечения плоскостей 2x-4y+5z-21=0,
x-3z+18=0, 6x+y+z-30=0 провести плоскость, параллельную
плоскости 3x-y-5z+6=0. Найти расстояние точки М1 (1; -1; -1)
до построенной плоскости.
Решение:
Решив систему уравнений, найдем точку пересечения
2 x 4 y 5 z 21 0
x 3 z 18 0
6 x y z 30 0
1 0 3 18
2 4 5 21
6 1 1 30
1 0 3 18
0 1 19 138
0 0 1 7
1
0
0
1
0
0
0 3 18 1 0 3 18
4 11 57 0 1 19 138
1 19 138 0 0 87 609
0 0 3
1 0 5 Получим точку М (3; 5; 7).
0 1 7

26.

Так как искомая плоскость параллельна плоскости
3x-y-5z+6=0 , то в качестве ее нормального вектора можно
взять нормальный вектор {3;-1;-5}.
3( x 3) ( y 5) 5( z 7) 0
3 x - y - 5 z 31 0
Pасстояние точки М1 (1; -1; -1) до построенной плоскости
d
d
Ax1 By1 Cz1 D
A2 B 2 C 2
3 1 1 ( 1) 5 ( 1) 31
32 ( 1) 2 ( 52 )
40
35

27.

§ 2. Различные виды уравнений прямой
в пространстве
Прямая в пространстве может быть задана:
- двумя точками;
- точкой и направляющим вектором;
- как пересечение двух плоскостей.
Уравнения прямой, проходящей через две заданные точки
M1(x1; y1; z1), M2(x2; y2; z2)
M
M2
Пусть M(x; y; z) – произвольная точка
M1
этой прямой.
M1, M2, M лежат на одной прямой M 1M M 1M 2 , т. е.
x x1
y y1
z z1
.
x2 x1 y2 y1 z2 z1
(1)
Пример 1. Напишем уравнения прямой, проходящей через
точки M1(1; 2; 3), M2(5; 4; 3).
x 1 y 2 z 3
x 1 y 2 z 3 x 1 y 2 z 3
.
;
;
2
1
0
5 1 4 2 3 3
4
2
0

28.

Канонические уравнения прямой
Напишем уравнения прямой, проходящей через данную
точку M0(x0; y0; z0) параллельно заданному вектору s {m; n; p}.
Опр. 1. Вектор, параллельный прямой, называется
направляющим вектором этой прямой.
Замечание. Направляющим вектором прямой является любой
вектор, параллельный этой прямой.
s
Пусть M(x; y; z) – произвольная точка
M
этой прямой.
M0
M лежит на этой прямой M 0 M s , т. е.
x x0 y y0 z z0
.
m
n
p
(2)
Уравнения (2), где (x0; y0; z0) – координаты точки, лежащей на
прямой, а s {m; n; p} – направляющий вектор прямой, называются
каноническими уравнениями прямой в пространстве и
представляют собой наиболее удобный способ записи уравнений
прямой в пространстве.

29.

Параметрические уравнения прямой
x x0
m t,
y y0
t,
n
z z0
p t,
где t – некоторый
параметр.
Параметрические уравнения прямой
x x0 mt ,
y y0 nt ,
z z pt ,
0
где (x0; y0; z0) – координаты точки, лежащей
на прямой, а s {m; n; p} – направляющий
вектор прямой.
Пример 1 (продолжение). Напишем параметрические уравнения
прямой, проходящей через точки M1(1; 2; 3), M2(5; 4; 3).
x 1 y 2 z 3
t
2
1
0
x 1 2t ,
y 2 t,
z 3.

30.

Общие уравнения прямой
Так как каждая прямая всегда может быть помещена в
некоторую плоскость и при пересечении двух плоскостей
образуется прямая, то в аналитической геометрии прямую в
пространстве принято задавать как пересечение двух
плоскостей.
Общими уравнениями прямой в пространстве называются
A1 x B1 y C1z D1 0,
A2 x B2 y C2 z D2 0,
т. е. прямая задается как пересечение двух плоскостей.
Так как через любую прямую в пространстве проходит
множество плоскостей, то любую прямую можно задать ее
общими уравнениями и не единственным образом.
Недостатком задания прямой общими уравнениями является то,
что по их виду ничего нельзя сказать о расположении прямой в
пространстве. При решении задач удобнее использовать другие,
более наглядные формы записи уравнений прямой –
параметрические или канонические уравнения.

31.

Общими уравнениями прямой в пространстве называются
A1 x B1 y C1z D1 0,
A2 x B2 y C2 z D2 0,
т. е. прямая задается как пересечение двух плоскостей.
n1
Пример 2. Напишем канонические уравнения прямой
s {m; n; p}
x 3 y 2 z 9 0,
2 x 4 y z 4 0.
n1 {1; 3; 2}, n2 {2; 4;1}.
?
s
n2
i j k
s n1 n2 1 3 2 5i 3 j 2k . Таким образом, m 5; n 3; p 2.
2 4 1
x 3 y 9 0, x 3 y 9,
M0(x0; y0; z0).
Пусть z = 0,
2 x 4 y 4 0; 2 x 4 y 4.
1 9
9 3
2 4 14
4 4
24
7,
y
12;
x
2
1 3
1 3
2
2 4
2 4
?

32.

Общими уравнениями прямой в пространстве называются
A1 x B1 y C1z D1 0,
A2 x B2 y C2 z D2 0,
т. е. прямая задается как пересечение двух плоскостей.
n1
Пример 2. Напишем канонические уравнения прямой
s {m; n; p}
x 3 y 2 z 9 0,
2 x 4 y z 4 0.
n1 {1; 3; 2}, n2 {2; 4;1}.
?
s
n2
i j k
s n1 n2 1 3 2 5i 3 j 2k . Таким образом, m 5; n 3; p 2.
2 4 1
x 12;
x 3 y 9 0, x 3 y 9,
M0(x0; y0; z0).
Пусть z = 0,
y 7.
2 x 4 y 4 0; 2 x 4 y 4.
?
Таким образом, M0(–12; 7; 0).
x 12 y 7 z
.
5
3
2

33.

Взаимное расположение прямых в пространстве
Если в пространстве даны две прямые, то они могут
1) быть параллельны,
2) пересекаться,
3) скрещиваться.
Если прямые параллельны, то их
направляющие векторы коллинеарные l1 / / l2
(имеют
пропорциональные
координаты).
Теперь рассмотрим две пересекающиеся
прямые. Такие прямые можно поместить
в одну плоскость. Но это значит, что
векторы l1 m1; n1; p1 l2 m2 ; n2 ; p2
M 1M 2 x2 x1; y2 y1; z2 z1
будут компланарны. Следовательно,
M 1M 2 l1 l2 0

34.

или, в координатной форме
x2 x1
m1
m2
y2 y1
n1
n2
z2 z1
p1 0
p2
Таким образом, если прямые l1 и l2 не параллельны и для
них не выполняется условие M 1M 2 l1 l2 0 (или, в
координатной форме), то они скрещиваются.
x2 x1
m1
m2
y2 y1
n1
n2
z2 z1
p1 0
p2
Углом между двумя скрещивающимися прямыми l1 и l2
называется угол между прямой l1 и проекцией прямой l2 на
любую плоскость, проходящую через прямую l1.
2
Иначе говоря, угол между
2
скрещивающимися прямыми –
1
1
это
угол
между
двумя
1
пересекающимися прямыми,
2
2
параллельными данным

35.

Взаимное расположение двух прямых в пространстве
l1 {m1; n1; p1};
l1: x x1 y y1 z z1 ;
m1
n1
p1
x x2 y y2 z z2
l2 {m2 ; n2 ; p2 }.
.
l2:
m2
n2
p2
Угол между двумя прямыми
cos
l1 l2
l1 l2
cos
,
m1m2 n1n2 p1 p2
m12 n12 p12
m22 n22 p22
.
Замечание. Для нахождения острого угла следует взять
модуль правой части.
Условие параллельности двух прямых.
l1 l2
l1 l2 ,
т. е.
m1 n1 p1
.
m2 n2 p2
Условие перпендикулярности двух прямых.
l1 l2
l1 l2 ,
l1 l2 0.
m1m2 n1n2 p1 p2 0.

36.

Взаимное
расположение
в пространстве
прямой
и
плоскости
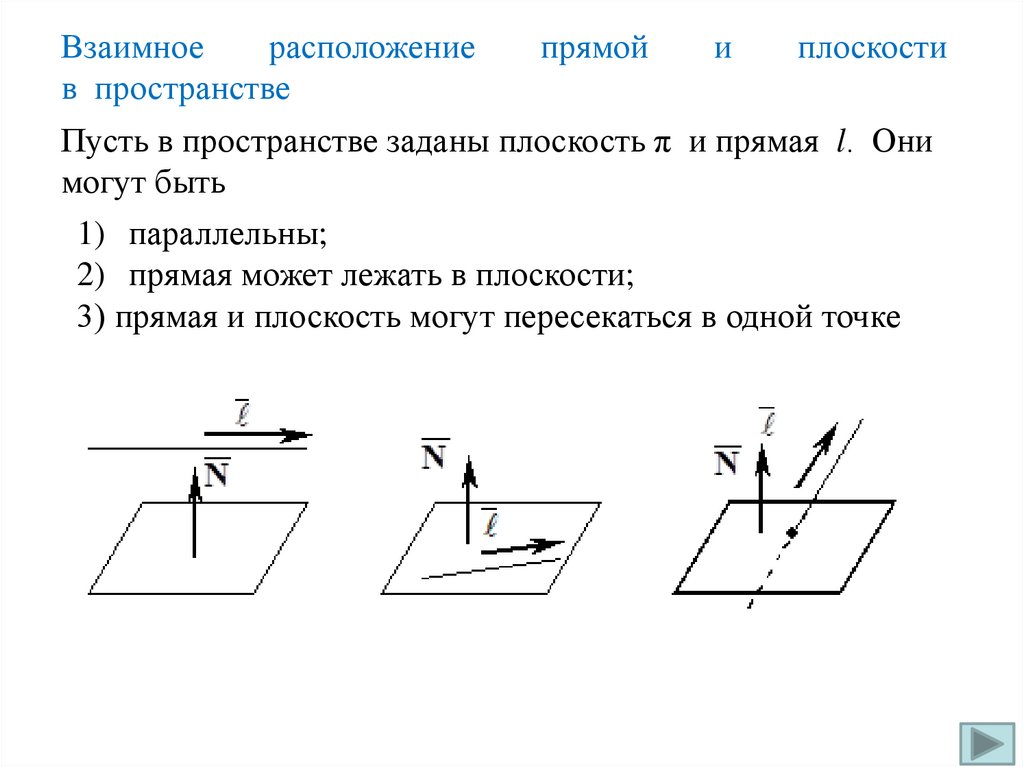
Пусть в пространстве заданы плоскость π и прямая l. Они
могут быть
1) параллельны;
2) прямая может лежать в плоскости;
3) прямая и плоскость могут пересекаться в одной точке

37.

Взаимное расположение прямой и плоскости в пространстве
x x0 y y0 z z0
,
m
n
p
s {m; n; p};
П : Ax By Cz D 0.
n { A; B; C}.
l:
Угол между прямой и плоскостью
cos(90 )
n s
n s
, sin
n s
n s
, sin
n
s
l
φ
П
| Am Bn Cp |
A2 B 2 C 2 m 2 n 2 p 2
.
Замечание. Поскольку sin φ ≥ 0, то числитель дроби взят по модулю.
n
Условие параллельности прямой и плоскости.
s
l П s n или n s 0. Am Bn Cp 0.
Условие перпендикулярности прямой и плоскости.
l П n s,
A B C
.
m n p
n
s

38.

Теперь укажем условие, которое позволит различать случай
параллельности прямой и плоскости и случай, когда прямая
принадлежит плоскости.
Пусть прямая l лежит в плоскости π. Тогда любая точка
прямой лежит в плоскости и, следовательно, ее координаты
удовлетворяют уравнению плоскости. В частности,
Ax0 By0 Cz0 D 0
где M0(x0;y0;z0) – некоторая фиксированная точка прямой l.
Если же прямая параллельна плоскости, то она не имеет
общих точек с плоскостью и, следовательно, для такой
прямой
Ax0 By0 Cz0 D 0
Таким образом, если прямая лежит в плоскости, то должны
выполняться два условия: Ax0 By0 Cz0 D 0 и Am Bn Cp 0.
если же прямая параллельна плоскости, то
Ax0 By0 Cz0 D 0
Am Bn Cp 0.

39.

Расстояние от точки до прямой в пространстве.
Пусть дана прямая
l:
x x0 y y0 z z0
,
m
n
p
и точка M1(x1;y1;z1), не
принадлежащая этой прямой.
Обозначим l (m , n , p )
– направляющий вектор прямой
l, M0(x0;y0;z0) – некоторая точка на прямой l, d– расстояние от
точки M1 до прямой l.
Рассмотрим параллелограмм, построенный на векторах l и M 0 M 1
Тогда d – высота этого параллелограмма, опущенная из
вершины M1 . Следовательно,
l M 0M1
d
l