ВиС-10_Формула Байеса- д

1.

10 класс
Формула Байеса
1 урок

2.

Формула Байеса
Британский математик и священник
Томас
Байес
(1702—1761)
опубликовал при жизни всего две
работы — одну богословскую,
другую математическую.
Тем не менее сегодня без его имени не обходится ни один
учебник по теории вероятностей. В его работе,
опубликованной в 1763 г. уже после смерти автора, был
предложен «метод для корректировки убеждений,
основанный на обновлённых данных».

3.

Формула Байеса

4.

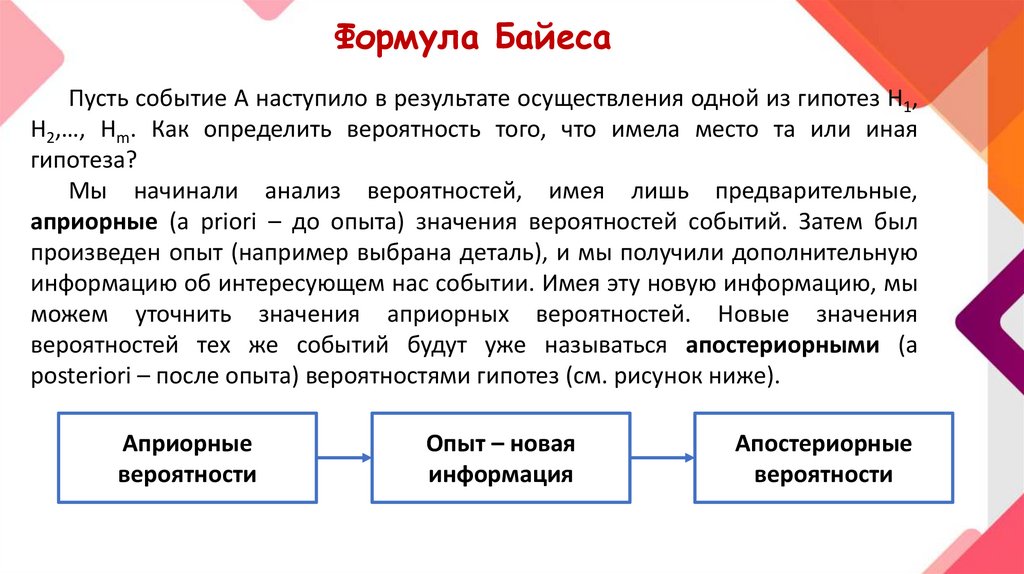
Формула Байеса
Пусть событие А наступило в результате осуществления одной из гипотез Н1,
Н2,…, Нm. Как определить вероятность того, что имела место та или иная
гипотеза?
Мы начинали анализ вероятностей, имея лишь предварительные,
априорные (a priori – до опыта) значения вероятностей событий. Затем был
произведен опыт (например выбрана деталь), и мы получили дополнительную
информацию об интересующем нас событии. Имея эту новую информацию, мы
можем уточнить значения априорных вероятностей. Новые значения
вероятностей тех же событий будут уже называться апостериорными (a
posteriori – после опыта) вероятностями гипотез (см. рисунок ниже).
Априорные
вероятности
Опыт – новая
информация
Апостериорные
вероятности

5.

Формула Байеса

6.

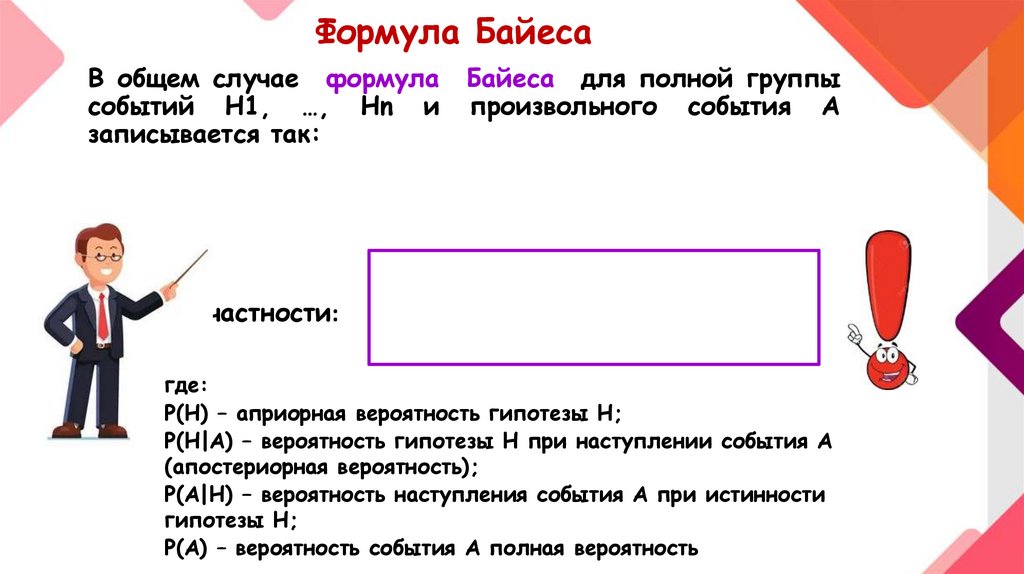
Формула Байеса
В общем случае формула
событий H1, …, Hn и
записывается так:
Байеса для полной группы
произвольного события A
В частности:
где:
P(H) – априорная вероятность гипотезы H;
P(H|A) – вероятность гипотезы H при наступлении события A
(апостериорная вероятность);
P(A|H) – вероятность наступления события A при истинности
гипотезы H;
P(A) – вероятность события A полная вероятность

7.

Формула Байеса. Рассмотрим пример
ПРИМЕР 1. Смартфоны марки «Бетафон» производятся на трёх заводах.
При этом 20% всей продукции выпускает первый завод, 30% — второй,
50% — третий. Процент брака на каждом из этих заводов составляет
соответственно 4%, 2% и 1%. Какова вероятность, что случайно
выбранный смартфон будет бракованным?
Чтобы найти P(A), применим формулу полной вероятности:
P(A) = 0,2 · 0,04 + 0,3 · 0,02 + 0,5 · 0,01 = 0,008 + 0,006 + 0,005 = 0,019

8.

Формула Байеса. Рассмотрим пример
ПРИМЕР 1. Смартфоны марки «Бетафон» производятся на трёх заводах.
При этом 20% всей продукции выпускает первый завод, 30% — второй,
50% — третий. Процент брака на каждом из этих заводов составляет
соответственно 4%, 2% и 1%. С какой вероятностью выбранный смартфон
будет бракованным и он был сделан на первом заводе?
P(A) = 0,019

9.

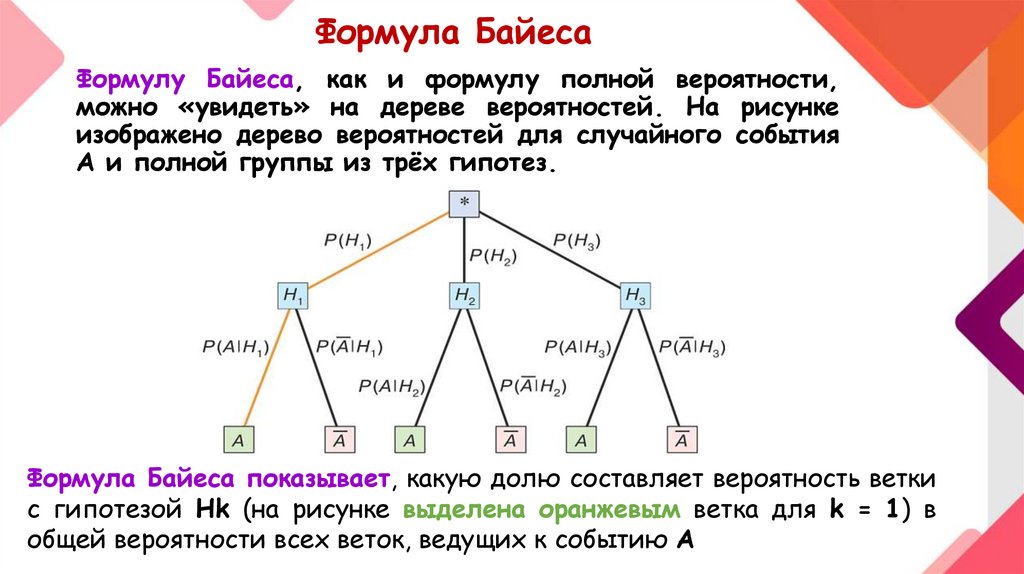
Формула Байеса
Формулу Байеса, как и формулу полной вероятности,
можно «увидеть» на дереве вероятностей. На рисунке
изображено дерево вероятностей для случайного события
A и полной группы из трёх гипотез.
Формула Байеса показывает, какую долю составляет вероятность ветки
с гипотезой Hk (на рисунке выделена оранжевым ветка для k = 1) в
общей вероятности всех веток, ведущих к событию A

10.

Работаем в тетради
Задача 1. На хим. заводе установлена система аварийной сигнализации.
Когда возникает аварийная ситуация звуковой сигнал срабатывает с
вероятностью 0,95, звуковой сигнал может срабатывать случайно и без
аварийной ситуации с вероятностью 0,05, реальная вероятность аварийной
ситуации равна 0,004. Предположим, звуковой сигнал сработал. Чему равна
вероятность реальной аварийной ситуации ?
Решение. Обозначим событие: A - срабатывание системы аварийной сигнализации
(срабатывание звукового сигнала).
Чтобы найти P(A), применим формулу полной вероятности:
P(A) = 0,95 · 0,004 + 0,05 · 0,996 = 0,0536

11.

Выполните задание в тетради
Задание 2. На контроль поступают одинаковые блюда, изготовленные
двумя поварами. Производительность первого повара вдвое больше,
чем второго. Процент брака у первого 0.08, а у второго - 0.06.
Проверенное блюдо не удовлетворяет требованиям контроля. Найти
вероятность того, что блюдо приготовлено первым поваром.
Решение. Обозначим событие: A - проверенное блюдо не удовлетворяет
требованиям контроля.

12.

Работаем в тетради
Задача 3. Три сестры Алиса, Ира и Соня поочерёдно моют посуду.
Вероятность разбить тарелку для Алисы – 0,04, для Иры – 0,03, для
Сони – 0,02. Какова вероятность того, что Алиса мыла посуду, если
родители услышали звон разбитой тарелки?

13.

Работаем в тетради
Задача 4. Пассажир может приобрести в одной из трёх касс.
Вероятность обращения в ту или иную кассу равны 0,2; 0,3; 0,5.
вероятность того, что к моменту прихода пассажира к кассе все
билеты будут проданы, равна 0,2; 0,3; 0,4. Определите вероятность
того, что пассажир купит билет, и ответьте на вопрос, в какой кассе
вероятнее всего он купит билет?
Вероятнее всего билет будет куплен в третьей кассе

14.

Работаем в тетради
Задача 5. В группе из 10 студентов, пришедших на экзамен,
3 подготовились отлично, 4 – хорошо, 2 – удовлетворительно и 1
– плохо. В экзаменационных билетах 20 вопросов. Отлично
подготовленный студент может ответить на 20 вопросов, хорошо
подготовленный – на 16, удовлетворительно – на 10, плохо – на
5. Вызванный наугад студент ответил на 3 произвольно заданных
вопроса. Найдите вероятность того, что этот студен подготовлен:
а) отлично;
б) плохо.
Чтобы найти P(A), применим формулу полной вероятности:
P(A) = 0,3 · 1 + 0,4 · 0,491 + 0,2 · 0,105 + 0,1 · 0,009 = 0,5183

15.

Источники
1. Бунимович, Евгений Абрамович. Математика. Вероятность
и статистика : 10-й класс : базовый и углублённый уровни :
учебное пособие / Е. А. Бунимович, В. А. Булычев. —
Москва : Просвещение, 2023. — 223 с.
2. https://ptlab.mccme.ru/vertical