Теория вероятностей и математическая статистика

Вероятность появления хотя бы одного события

499.98K

Category: $mathematics$ mathematics

1. Теория вероятностей и математическая статистика

3. ВЕРОЯТНОСТЬ СЛУЧАЙНЫХ
СОБЫТИЙ

2. Вероятность события А

Количественной характеристикой возможности наступления случайного
события является его вероятность.
Классическая схема применяется, если пространство элементарных исходов
конечно и все элементарные события одинаково возможны.
Probabilitas – вероятность
обозначение
m
P A
n
число исходов, при которых
событие А происходит
число всех исходов
• где п – общее число элементарных исходов;
• m – число исходов, благоприятствующих
событию А (элементарные исходы, в
которых событие А наступает).

3. Геометрическое определение вероятности

Пространство элементарных исходов бесконечно, но эти
события являются одинаково возможными.
• Множество элементарных исходов представимо в виде
отрезка прямой, или фигуры на плоскости, или тела в
пространстве.
• Событие А состоит в случайном попадании «брошенной»
точки в некоторую область G (область, благоприятная для
события А).
mes(G) мера области G
P( A)
mes( ) мера всего пространства
элементарных исходов

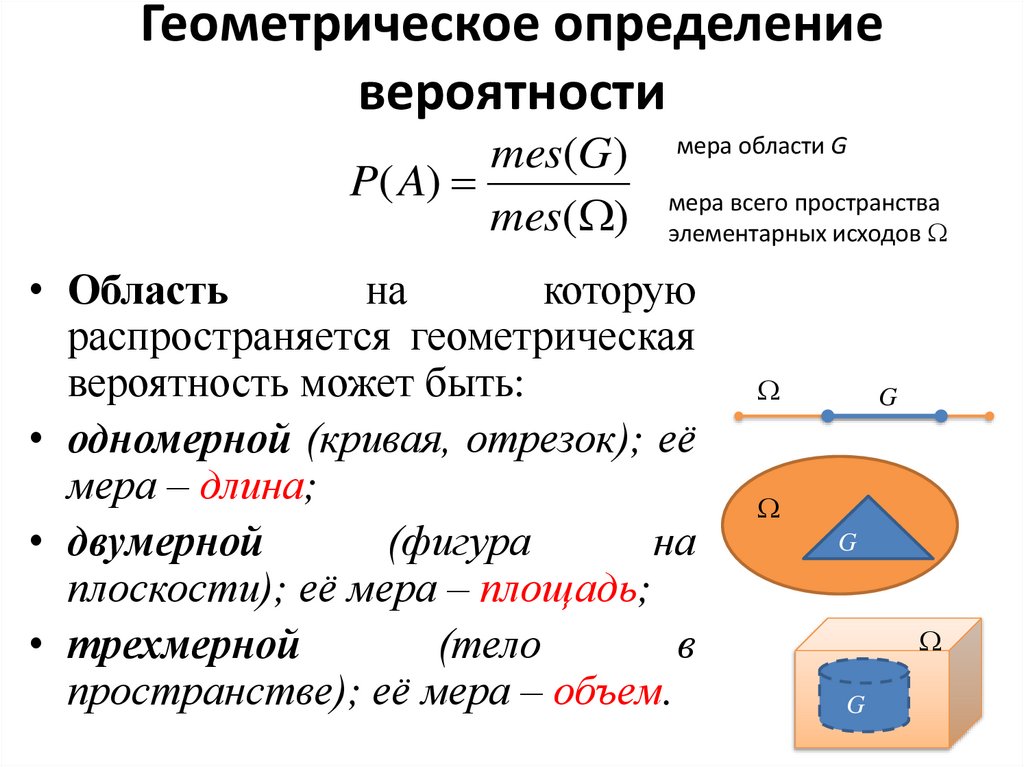
4. Геометрическое определение вероятности

mes(G)
P( A)
mes( )
мера области G
мера всего пространства
элементарных исходов
• Область
на
которую
распространяется геометрическая
вероятность может быть:
• одномерной (кривая, отрезок); её
мера – длина;
• двумерной
(фигура
на
плоскости); её мера – площадь;
• трехмерной
(тело
в
пространстве); её мера – объем.
G
G
G

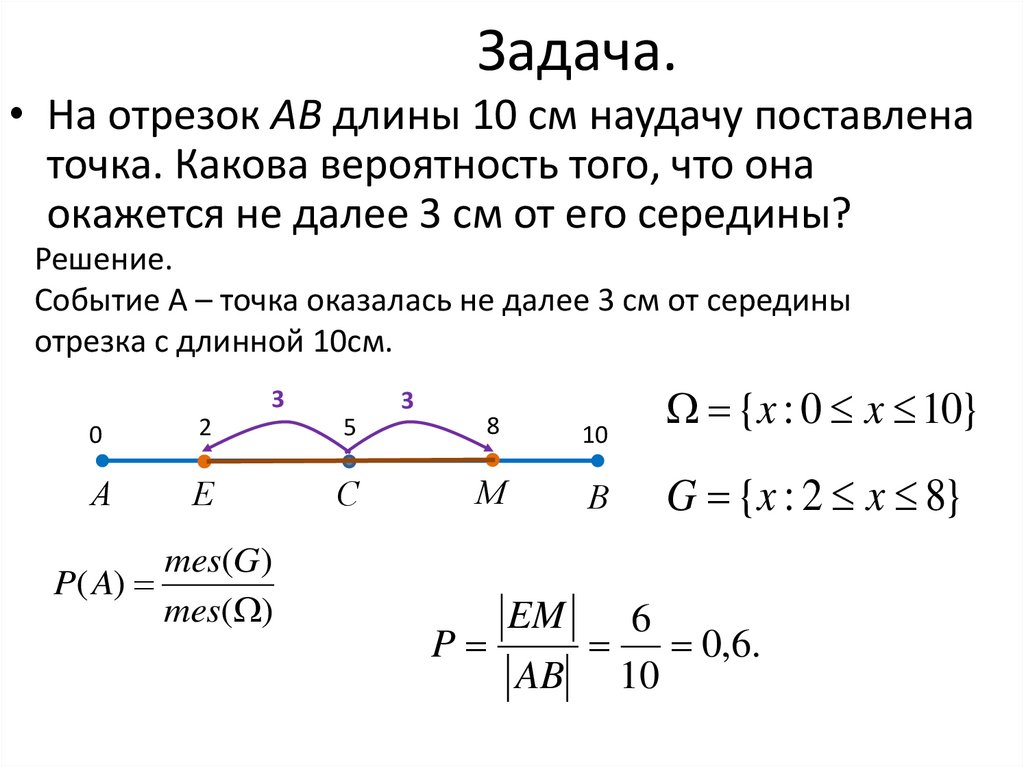
5. Задача.

• На отрезок АВ длины 10 см наудачу поставлена
точка. Какова вероятность того, что она
окажется не далее 3 см от его середины?
Решение.
Событие А – точка оказалась не далее 3 см от середины
отрезка с длинной 10см.
3
3
0
2
5
8
10
А
Е
С
М
В
mes(G)
P( A)
mes( )
EM
{x : 0 x 10}
G {x : 2 x 8}
6
P
0,6.
AB 10

6. Статистическое определение вероятности

Проводится серия из n испытаний, в каждом из которых
случайное событие А наблюдается т раз (частота события А).
Частота характеризуется изменчивостью и устойчивостью
• Относительная частота события А –
отношение числа испытаний m , в которых
событие А появилось, к общему числу
произведенных испытаний п.
относительная частота
m
~
P A lim
n n
число произведенных
испытаний стремится к
бесконечности
частота (число исходов, в
которых событие А
наблюдалось)
число всех испытаний

7. Свойства вероятности

1. Вероятность достоверного события
равна единице. P( ) n 1
n
2. Вероятность невозможного события
0
равна нулю.
P ( ) 0
n
3. Вероятность случайного события есть
положительное число, заключенное между
нулем и единицей.
0 P( A) 1

8.

Статистическая схема
Эксперименты
• Соревнование между
игроками
• Точность попадания
• Наблюдение за качеством
товара, за предпочтениями
клиентов, за исправностью
технических средств,
безошибочностью работы
• Выбор направления
движения, из категорий
разной популярности
• Соответствие людей
определенной категории
(профессия, рост, место
жительства)
Классическая схема
• Подбрасывание кубиков,
монет
• Выбор из внешне
неразличимых элементов
(карты, домино,
штампованные детали,
шары в урне, жетоны,
лотереи, билеты, карточки)
• Угадывание цифр,
использование генератора
случайных чисел
• Раскручивание рулетки
• Автоматическая стрельба
(не настраиваемая)

9.

Выделяются следующие интерпретации вероятности:
• классическая (вероятность как отношение благоприятных случаев
наступления какого-либо события к числу всех возможных случаев);
• частотная (вероятность как частота появления событий одного класса среди
событий другого класса);
• эпистемологическая (вероятность как степень логического подтверждения
некоторой гипотезы данными);
• логическая (вероятность как степень логической выводимости одних
высказываний из других);
• диспозиционная (вероятность как степень объективной возможности
наступления некоторого события при определенных условиях);
• субъективная (вероятность как степень уверенности субъекта в истинности
некоторого высказывания или в наступлении некоторого события).
«Но ни одна из существующих интерпретаций вероятности не
универсальна, поскольку не в состоянии ассимилировать все существующие
контексты употребления категории «вероятность» в науке, повседневной
жизни и практической деятельности».
Лебедев С.А. Методологический анализ категории "вероятность" // Гуманитарный вестник. 2017.
№11 (61). URL: https://cyberleninka.ru/article/n/metodologicheskiy-analiz-kategorii-veroyatnost.

10. Теория вероятностей

Основные формулы для
вычисления вероятностей

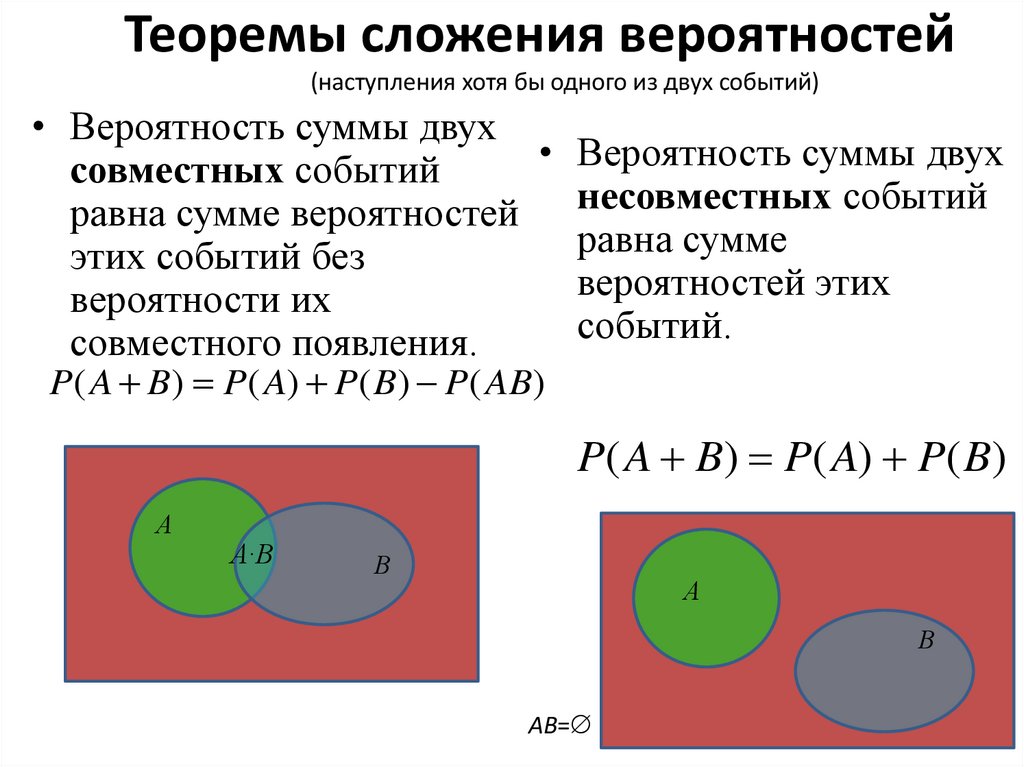
11. Теоремы сложения вероятностей

(наступления хотя бы одного из двух событий)
• Вероятность суммы двух
• Вероятность суммы двух
совместных событий
равна сумме вероятностей несовместных событий
равна сумме
этих событий без
вероятностей этих
вероятности их
событий.
совместного появления.
P( A B) P( A) P( B) P( AB)
P( A B) P( A) P( B)
А
А∙В
В
А
В
АВ=

12. Следствия теоремы сложения

• Для любого конечного числа попарно
несовместных событий А1, А2, , Аn выполняется
равенство
Р( A1 A2 ... An ) Р( A1 ) Р( A2 ) ... Р( An ).
• Если события А1, А2, , Аn образуют полную
группу, то
Р( A1 ) Р( A2 ) ... Р( An ) 1.
• Сумма вероятностей противоположных событий
равна единице: P( A) P( A) 1
P( A) p
А
P( A) q
A
p q 1
q 1 p

13. Следствия теоремы сложения

• Теорема сложения обобщается на случай трех и
более слагаемых.
• Суммы трех совместных событий
А
В
А∙В
А∙В∙С
А∙С
С∙В
С
P( A B C ) P( A) P( B) P(C ) P( AB) P( AC ) P( BC ) P( ABC )

14. Условная вероятность

• Вероятность события В, вычисленная при
условии, что произошло событие А, называется
условной вероятностью события В
PA (B)
P( B | A)
Событие В называют независимым от
события А, если появление события А не
изменяет вероятности события В, т. е. если
условная вероятность события В равна его
безусловной вероятности
P( B | A) P( B)

15. Теорема умножения вероятностей

• Вероятность произведения • Вероятность
двух (зависимых) событий
произведения двух
равна произведению
независимых событий
вероятности одного из них
равна произведению
на условную вероятность
вероятностей этих
другого, при условии, что
событий.
первое событие уже
P( AB ) P( A) P( B)
произошло.
P( AB) P( A) P( B | A)
P( AB) P( B) P( A | B)

16. Следствия теоремы умножения

• Для независимых событий справедливо
равенство
P( A1 A2 ... An ) P( A1 ) P( A2 ) ... P( An ).
• Для любого конечного числа зависимых
событий
P( ABC MN ) P( A) P( B А) P(C АВ) P( N ABC M )
Р( А1 А2 А3 ) Р( А1 ) Р( А2 А1 ) Р( А3 А1 А2 )

17. Вероятность появления хотя бы одного события

• Вероятность появления хотя бы одного из
событий A1 , A2 , ..., An , независимых в
совокупности, равна разности между
единицей и произведением вероятностей
противоположных событий.
P( A1 A2 ... An ) 1 P( A1 ) P( A2 )...P( An ) 1 q1q2 qn .
A1 , A2 , ..., An
• Если независимые события
имеют одинаковую вероятность, равную р, то
вероятность появления хотя бы одного из этих
n
событий
P( A) 1 q

18. Формула полной вероятности

• Пусть событие А может происходить в различных
условиях, о характере которых можно выдвинуть
n гипотез Н1, Н2, …, Нп – п событий образующих
полную группу. Из некоторых соображений
известны вероятности P(Hi) гипотез до
проведения испытания (априорные
вероятности), известны также условные
вероятности события А по каждой гипотезе.
• Формула полной вероятности позволяет
вычислять вероятность события А, которое может
произойти вместе с одной из гипотез
n
P( A) P( H i ) PHi ( A).
i 1

19. Формулы Байеса

• Формулы Байеса позволяет вычислить вероятности
гипотез после наступления события А –
апостериорные вероятности PA(Hi) гипотез.
• Пусть события Н1, Н2, …, Нп образуют полную
группу, и в результате испытания произошло
событие А. Тогда вероятность того, что при этом
была реализована гипотеза с номером k,
вычисляется по формуле
РA ( H k )
Р( H k А)
P( H k ) PH k ( A)
P( A)
P( H k ) P( А H k )
n
P( H ) P( А H )
i 1
i
i
,
k 1,2, ,n.

20.

• Задача 1. Две фабрики одной фирмы выпускают одинаковые
мобильные телефоны. Первая фабрика выпускает 30% всех
телефонов этой марки, а вторая—остальные телефоны.
Известно, что из всех телефонов, выпускаемых первой
фабрикой, 1% имеют скрытые дефекты, а из выпускаемых
второй фабрикой—1,5%. Найдите вероятность того, что
купленный в магазине телефон этой марки имеет скрытый
дефект.
Н1 – телефон выпущен 1-ой фабрикой Р(Н1)=0,3
Р(А|Н1)=0,01
Н2 – телефон выпущен 2-ой фабрикой Р(Н2)=0,7 Р(А|Н2)=0,015
А – телефон имеет скрытый дефект
n
P( A) P( H i ) PHi ( A). Р(H1 ) P( A | H1 ) Р(H 2 ) P( A | H 2 )
i 1
0,3 0,01 0,7 0,015

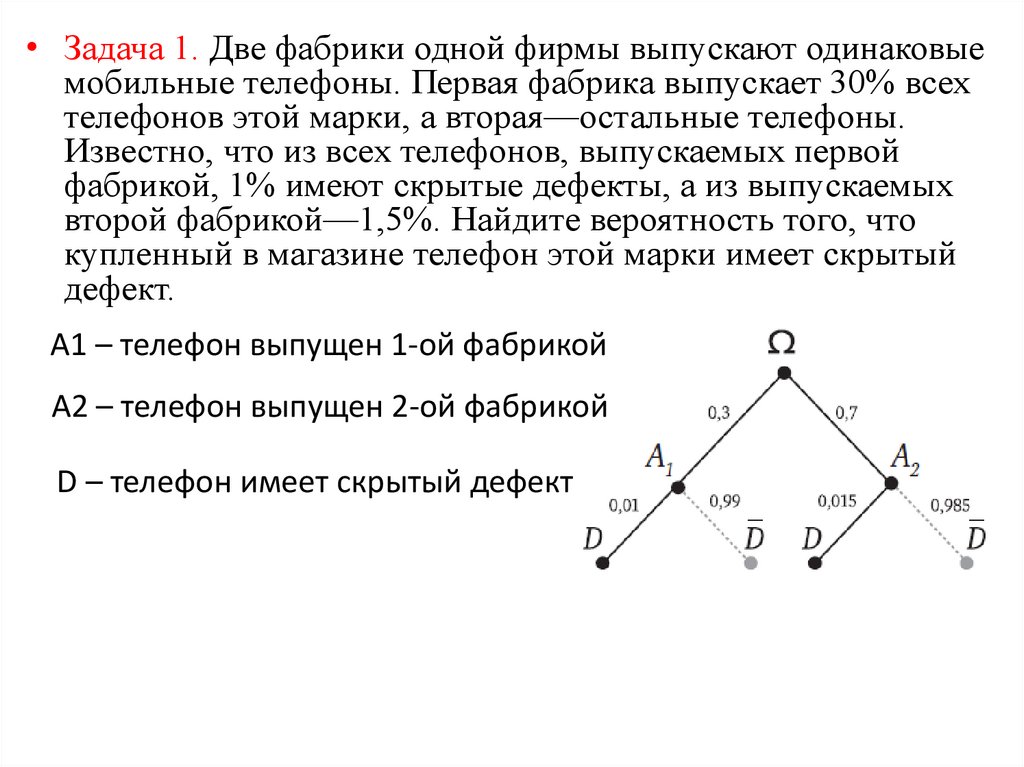
21.

• Задача 1. Две фабрики одной фирмы выпускают одинаковые
мобильные телефоны. Первая фабрика выпускает 30% всех
телефонов этой марки, а вторая—остальные телефоны.
Известно, что из всех телефонов, выпускаемых первой
фабрикой, 1% имеют скрытые дефекты, а из выпускаемых
второй фабрикой—1,5%. Найдите вероятность того, что
купленный в магазине телефон этой марки имеет скрытый
дефект.
A1 – телефон выпущен 1-ой фабрикой
A2 – телефон выпущен 2-ой фабрикой
D – телефон имеет скрытый дефект

22.

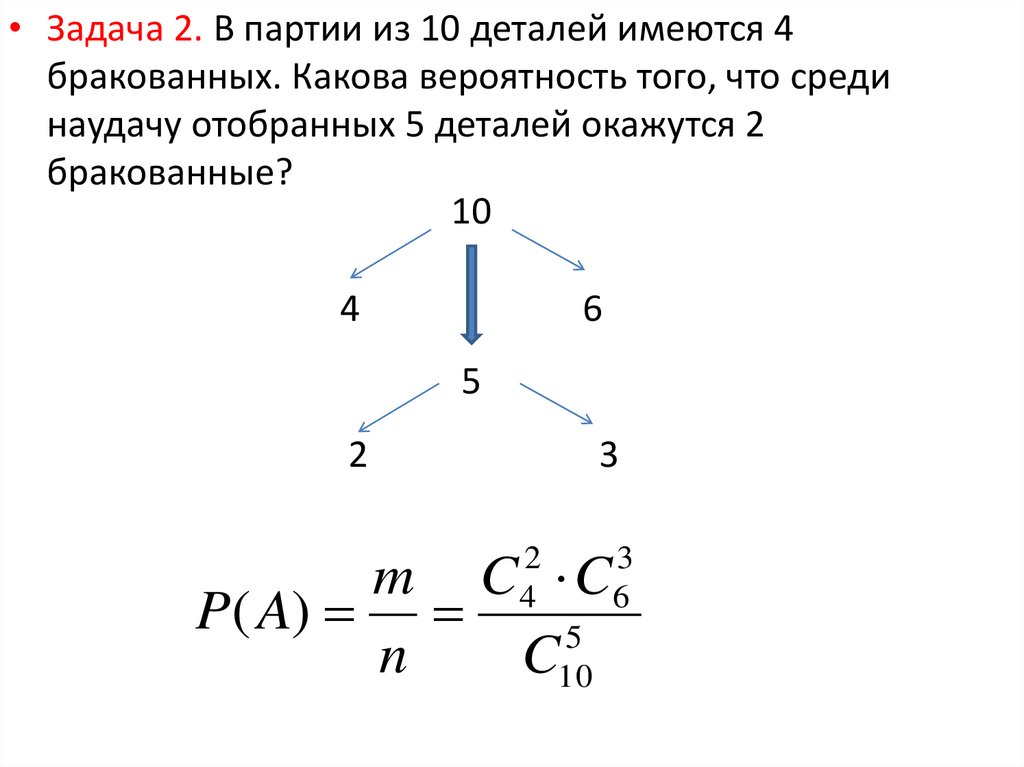
• Задача 2. В партии из 10 деталей имеются 4
бракованных. Какова вероятность того, что среди
наудачу отобранных 5 деталей окажутся 2
бракованные?
10
4
6
5
2
3
m C C
P( A)
5
n
C10
2
4
3
6

23.

24.

• Задача 3. Два зенитных орудия стреляют одновременно и
независимо друг от друга по самолету. Самолет сбит, если в
него попал хоть один снаряд. Какова вероятность сбить
самолет, если вероятность попадания первого снаряда
равна 0,8, а второго – 0,7?
Решение.
1 способ. Самолет сбит, если в него попало ИЛИ первое орудие, ИЛИ второе, ИЛИ оба
Р(А + В)=Р(А) + Р(В) – Р(АВ)= 0,8+0,7 – 0,8∙0,7=1,5 – 0,56=0,94.
2 способ. Самолет сбит, если в него попало ИЛИ первое орудие, а второе не попало, ИЛИ
второе попало, а первое не попало, ИЛИ попали оба орудия, т.е. речь идет о сумме трех
несовместных событий
1
2
2
1
1
2
P p q p q p p
Р(А+В)=0,8∙0,3 + 0,7∙0,2 + 0,8∙0,7=0,24 +0,14 + 0,56=0,94.
3 способ. Самолет не сбит, если в него оба орудия не попали
P q1 q2 0,2 0,3 0,06
P 1 P 1

25. 26. Задачи.

• Задача 4. В одном ящике 4 белых и 8 черных
шаров, в другой – 9 белых и 6 черных. Найти
вероятность того, что два шара будут белыми,
если: 1) первый вытащили из первого, а второй из
второго ящика; 2) один за другим шары достает из
первого ящика; 3) их достали из разных ящиков.
Решение.
2) Событие А – первый белый шар достали из первого ящика.
Событие С – второй белый шар так же достали из первого ящика.
Достали И первый белый, И второй белый
P( A С )
m 4 1 3
PA (С )
n 12 1 11
m
4
4 1
P( A)
n 4 8 12 3
P( A С) P( A) PA (C)
1 3
1
3 11 11

27. Задачи.

• Задача 4. В одном ящике 4 белых и 8 черных шаров, в другой –
9 белых и 6 черных. Найти вероятность того, что два шара
будут белыми, если: 1) первый вытащили из первого, а второй
из второго ящика; 2) один за другим шары достает из первого
ящика; 3) их достали из разных ящиков.
Решение.
3) Событие А – белый шар достали из первого ящика. Событие В – белый шар
достали из второго ящика. Событие С – второй белый шар достали из первого
ящика, а событие D - второй белый шар достали из второго ящика. Белые шары
достали из разных ящиков, т.е. ИЛИ из первого, ИЛИ из второго.
P( A С B D) P( A С) P( B D) P( A) PA (C) P( B) PB ( D)
P( A С) P( A) PA (C) 1 3 1
3 11
11
m
9
9 3 P ( D) m 9 1 8 4
B
P( В)
n 15 1 14 7
n 6 9 15 5
1 12 167
P ( A С B D) 11 35 385 0,43
P( B) PB ( D)
3 4 12
5 7 35

28.

• Задача 5. Среди партии товара 95% качественных
изделий. Выбирают 2 изделия. Какова вероятность
того, что среди них хотя бы одно окажется
исправным.
P( A B) 1 0,05 0,9975
2
• Задача 6. В ящике в случайном порядке расположены
20 деталей, причем 5 из них стандартные. Рабочий
берет наудачу 3 детали. Найти вероятность того, что
все взятые детали окажутся стандартными.
5 4 3
1
P( A B С ) P( A) PA ( B) PAB (C )
20 19 18 114

English Русский Rules