presentaciya

1.

Проверка статистических
гипотез: основ ы и
практическое применение
Современный подход к принятию решений на основе данных

2.

Что такое статистическая
гипотеза
Определение
Роль в исследованиях
Статистическая гипотеза — это
предположение о свойствах
генеральной совокупности или о
исследовательских вопросов
параметрах распределения
вероятностей, которое может быть
проверено на основе выборочных
данных.
Гипотезы формулируются до сбора
данных и выражаются в терминах
статистических параметров:
средних значений, дисперсий,
пропорций или распределений.
Формализация
Объективная оценка
утверждений
Контроль вероятности
ошибочных выводов
Основа для принятия решений в
науке и бизнесе

3.

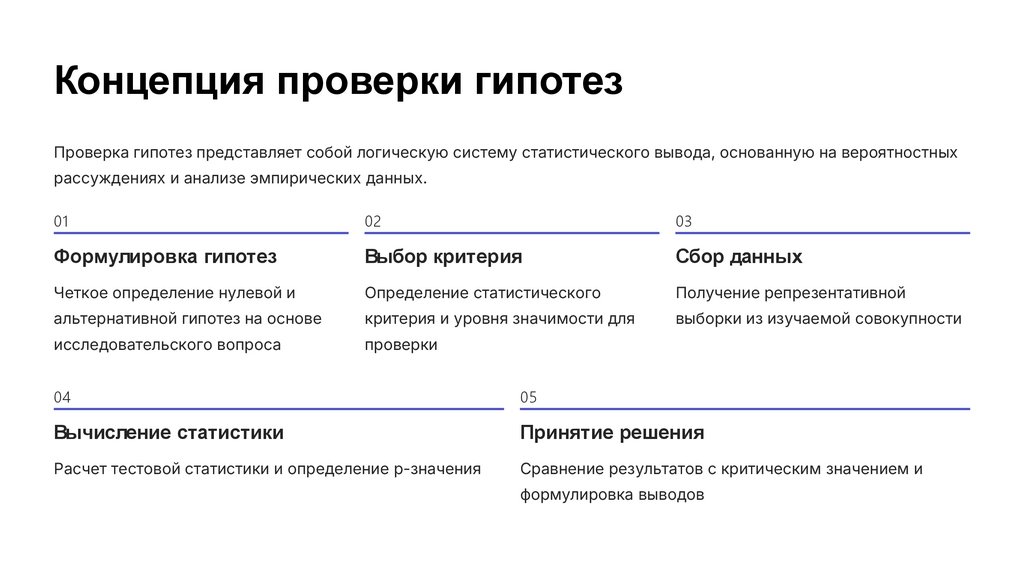
Концепция проверки гипотез
Проверка гипотез представляет собой логическую систему статистического вывода, основанную на вероятностных
рассуждениях и анализе эмпирических данных.
01
02
03
Формулировка гипотез
Выбор критерия
Сбор данных
Четкое определение нулевой и
Определение статистического
Получение репрезентативной
альтернативной гипотез на основе
критерия и уровня значимости для
выборки из изучаемой совокупности
исследовательского вопроса
проверки
04
05
Вычисление статистики
Принятие решения
Расчет тестовой статистики и определение p-значения
Сравнение результатов с критическим значением и
формулировка выводов

4.

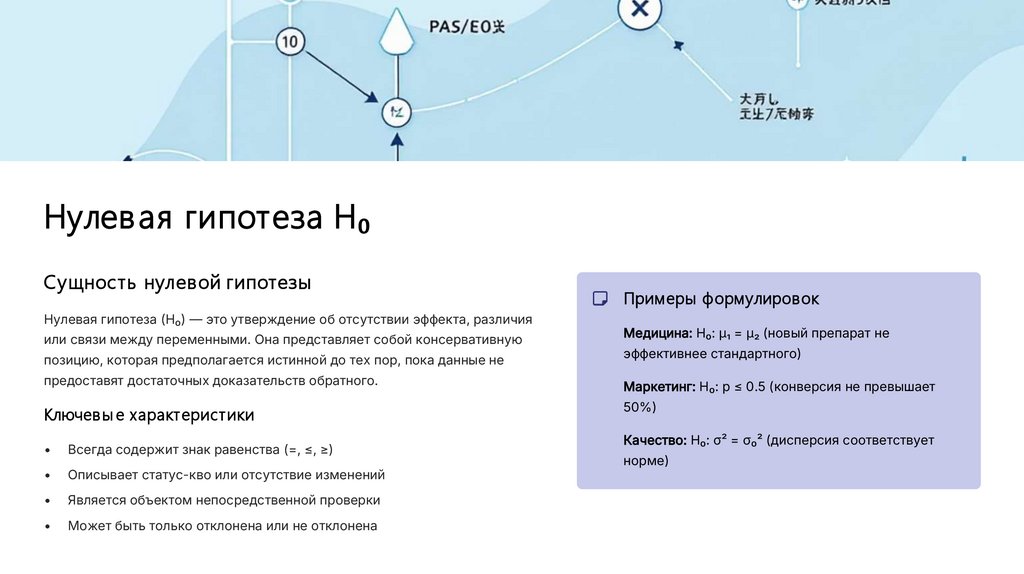
Нулевая гипотеза H₀
Сущность нулевой гипотезы
Нулевая гипотеза (H₀) — это утверждение об отсутствии эффекта, различия
или связи между переменными. Она представляет собой консервативную
позицию, которая предполагается истинной до тех пор, пока данные не
Примеры формулировок
Медицина: H₀: μ₁ = μ₂ (новый препарат не
эффективнее стандартного)
предоставят достаточных доказательств обратного.
Маркетинг: H₀: p ≤ 0.5 (конверсия не превышает
Ключев ы е характеристики
50%)
Всегда содержит знак равенства (=, ≤, ≥)
Описывает статус-кво или отсутствие изменений
Является объектом непосредственной проверки
Может быть только отклонена или не отклонена
Качество: H₀: σ² = σ₀² (дисперсия соответствует
норме)

5.

Альтернативная гипотеза H₁
Альтернативная гипотеза (H₁ или Hₐ) — это утверждение, которое принимается, если нулевая гипотеза отклоняется.
Она отражает исследовательское предположение или ожидаемый эффект.
Двусторонняя
Правосторонняя
Левосторонняя
H₁: μ ≠ μ₀
H₁: μ > μ₀
H₁: μ < μ₀
Параметр отличается от
Параметр больше заявленного
Параметр меньше заявленного
заявленного значения в любую
значения
значения
Пример: Новый метод
Пример: Улучшение снижает
увеличивает производительность
время обработки
сторону
Пример: Средний вес отличается
от 100 кг
Выбор типа альтернативной гипотезы зависит от исследовательского вопроса и направления ожидаемого эффекта.

6.

Процедура проверки гипотез
Ф ормулиров ка H₀ и H₁
Четкое определение проверяемых утверждений
Установ ка уров ня значимости α
Обычно α = 0.05, 0.01 или 0.10
Вы бор критерия и расчет
t-тест, z-тест, χ², F-тест и др.
Определение критической области
Значения, при которых H₀ отклоняется
Принятие решения
Сравнение и формулировка выводов

7.

Ошибка первого рода (α)
Определение
Ошибка первого рода возникает, когда мы отклоняем истинную нулевую гипотезу. Это
ложноположительный результат — мы обнаруживаем эффект, которого на самом деле нет.
Вероятнос ть и контроль
Вероятность ошибки первого рода обозначается буквой α (альфа) и называется уровнем
значимости. Исследователь устанавливает α заранее, обычно на уровне 0.05 (5%).
α = 0.05 — стандарт в социальных науках
α = 0.01 — более строгий критерий
α = 0.10 — менее строгий (разведочные исследования)

8.

Ошибка второго рода (β)
Определение
Ошибка второго рода происходит, когда мы не отклоняем ложную нулевую гипотезу. Это
ложноотрицательный результат — мы не обнаруживаем эффект, который существует.
Вероятность и факторы
Вероятность ошибки второго рода обозначается буквой β (бета). В отличие от α, значение β обычно не
контролируется напрямую.
Факторы, влияющие на β:
Размер выборки (больше n → меньше β)
Величина эффекта (больше эффект → меньше β)
Уровень значимости α (больше α → меньше β)
Вариабельность данных

9.

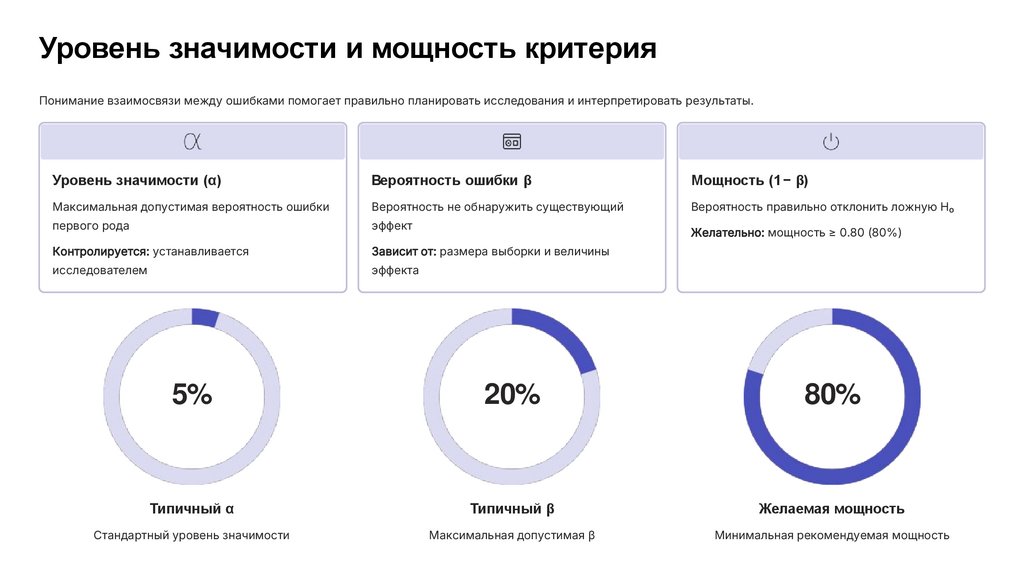
Уровень значимости и мощность критерия
Понимание взаимосвязи между ошибками помогает правильно планировать исследования и интерпретировать результаты.
Уровень значимости (α)
Вероятность ошибки β
Мощность (1 − β)
Максимальная допустимая вероятность ошибки
Вероятность не обнаружить существующий
Вероятность правильно отклонить ложную H₀
первого рода
эффект
Контролируется: устанавливается
Зависит от: размера выборки и величины
исследователем
эффекта
Желательно: мощность ≥ 0.80 (80%)
5%
20%
80%
Типичный α
Типичный β
Желаемая мощность
Стандартный уровень значимости
Максимальная допустимая β
Минимальная рекомендуемая мощность

10.

Практические рекомендации
Планирование
Анализ
Отчетность
Определяйте гипотезы до сбора данных
Проверяйте предпосылки
Сообщайте точные p-значения
Рассчитывайте необходимый размер
применимости тестов
Указывайте доверительные интервалы
Обсуждайте ограничения исследования
выборки
Интерпретируйте p-значения правильно
Учитывайте мощность критерия
Различайте статистическую и
практическую значимость
Ключевы е в ы воды
Проверка статистических гипотез — это мощный инструмент научного познания, требующий понимания баланса между ошибками первого и второго
рода. Правильное применение методологии позволяет принимать обоснованные решения на основе данных, контролируя риски ошибочных выводов.
Статистика не дает абсолютной истины, но предоставляет количественную меру уверенности в наших выводах.