Similar presentations:
Проверка статистических гипотез
1.
Проверкастатистических
гипотез
ТЮРНЕВА Т.Г.
ИМЭИ ИГУ
1
2.
Практическая работа №32
3.
Основные понятия◦ Статистическая гипотеза – это
предположение о значении параметров закона
распределения с.в. Х (параметрическая) или его
виде (непараметрическая).
◦ Статистическая гипотеза называется
простой, если она однозначно определяет
распределение с.в. Х; в противном случае,
гипотеза называется сложной.
3
4.
Основные понятияПроверяемую гипотезу обычно называют нулевой
(или основной) и обозначают Н0.
Наряду с нулевой гипотезой рассматривают
альтернативную (или конкурирующую) гипотезу Н1,
являющуюся логическим отрицанием Н0.
Выбор альтернативной гипотезы определяется
конкретной формулировкой задачи.
Проверка статистической гипотезы H состоит в
выяснении того, насколько эта гипотеза согласуется с
опытными данными X.
4
5.
Основные понятия◦ Решение – принять или отвергнуть гипотезу Н0 – принимается на
основании некоторого правила или критерия по выборочным
данным. При этом выбирается подходящая функция элементов
выборки, или статистика критерия, которую в общем случае будем
обозначать Z.
Правило, по которому принимается решение принять или
отклонить гипотезу Н0, называется критерием К.
◦ Принцип проверки статистических гипотез:
маловероятные события считаются невозможными, а события,
имеющие большую вероятность – достоверными.
5
6.
Принцип проверкистатистических гипотез
Реализация принципа:
◦ Задать уровень значимости α.
◦ Выбрать статистику Z критерия К;
◦ Множество значений статистики Z
разбить на непересекающиеся
подмножества – критическую
область и область принятия
гипотезы Н0.
6
7.
Критическая область◦ Множество значений статистики Z, при которых
принимается решение отклонить гипотезу Н0,
называется критической областью.
◦ Графически эта область определяется по кривой
распределения.
Уровень значимости α определяет «размер»
критической области
◦ Критическая
область
выбирается
так,
чтобы
вероятность попадания в нее была минимальной (равной
α), если верна нулевая гипотеза Н0, и максимальной в
противоположном случае.
7
8.
Критическая область◦ В зависимости от вида конкурирующей гипотезы и
распределения критерия выбирают вид расположения
критической области: правосторонняя, левосторонняя или
двусторонняя.
Границы (критические точки) при заданном уровне
значимости находят из соотношений для критических
областей:
правосторонней: P(Z > Zкр) = α;
левосторонней: P(Z < Zкр) = α;
двусторонней: P(Z < Zкр) = α /2 и P(Z > Zкр) = α /2.
8
9.
Область принятиярешения
Множество значений статистики Z,
при которых гипотеза Н0
принимается, называется областью
принятия решения.
9
10.
Критерий, основанный на использованиизаранее заданного уровня значимости α,
называют критерием значимости.
Проверка статистических гипотез может
быть проведена на основе
соответствующих доверительных
интервалов.
10
11.
Ошибки первого ивторого рода
Уровень значимости α – это вероятность ошибки первого
рода, т.е. вероятность того, что будет отвергнута гипотеза Н0, если
на самом деле для генеральной совокупности верна гипотеза Н0.
Значение α устанавливается на основе практического опыта в
различных областях исследования. Вероятность α задается
заранее малым числом: 0,05; 0,01; 0,005; 0,001.
Вероятность ошибки второго рода обозначают β – это
вероятность того, что будет принята гипотеза Н0, если на самом
деле верна гипотеза Н1.
Вероятность не совершить ошибку второго рода (1 – β), т. е.
вероятность правильного отклонения неверной нулевой
гипотезы, называют мощностью критерия.
11
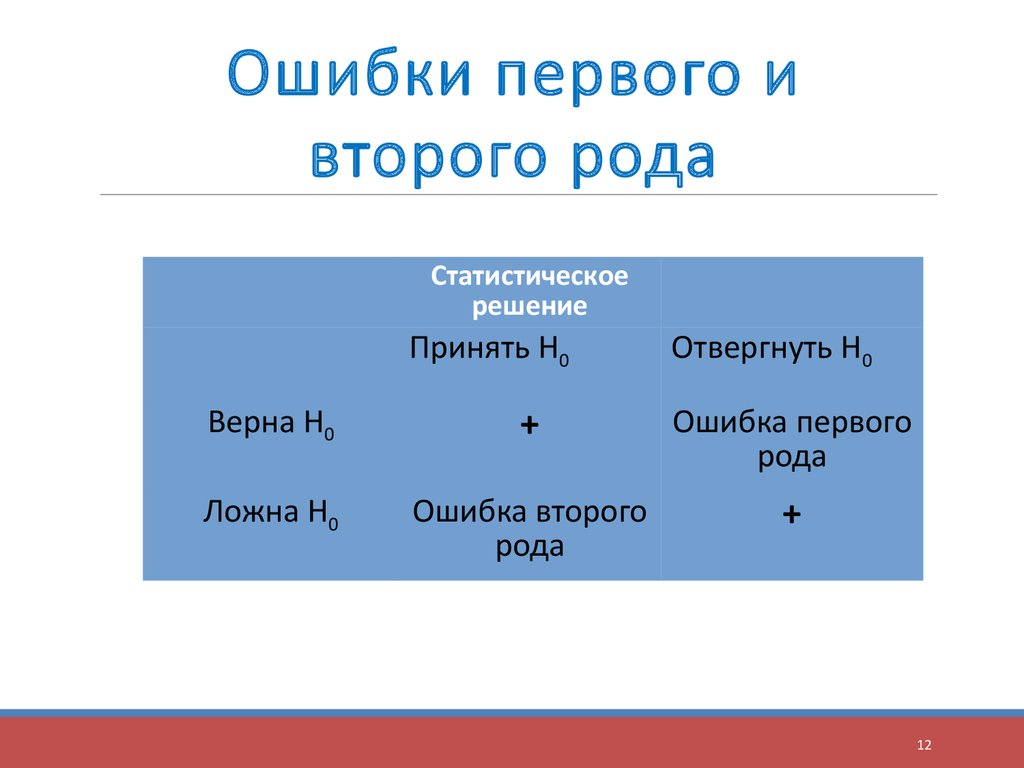
12.
Ошибки первого ивторого рода
Статистическое
решение
Принять Н0
Отвергнуть Н0
Верна Н0
+
Ошибка первого
рода
Ложна Н0
Ошибка второго
рода
+
12
13.
Ошибки первого ивторого рода
Статистическая ошибка первого рода (Type I Error) – ошибка
обнаружить различия или связи, которые на самом деле не
существуют!
Статистическая ошибка второго рода (Type II Error) - не обнаружить
различия или связи, которые на самом деле существуют
«Судебная» аналогия: Вердикт «Не виновен» или «Виновен»
Ошибка первого рода - невинный обвинен
Ошибка второго рода - виновный освобожден
13
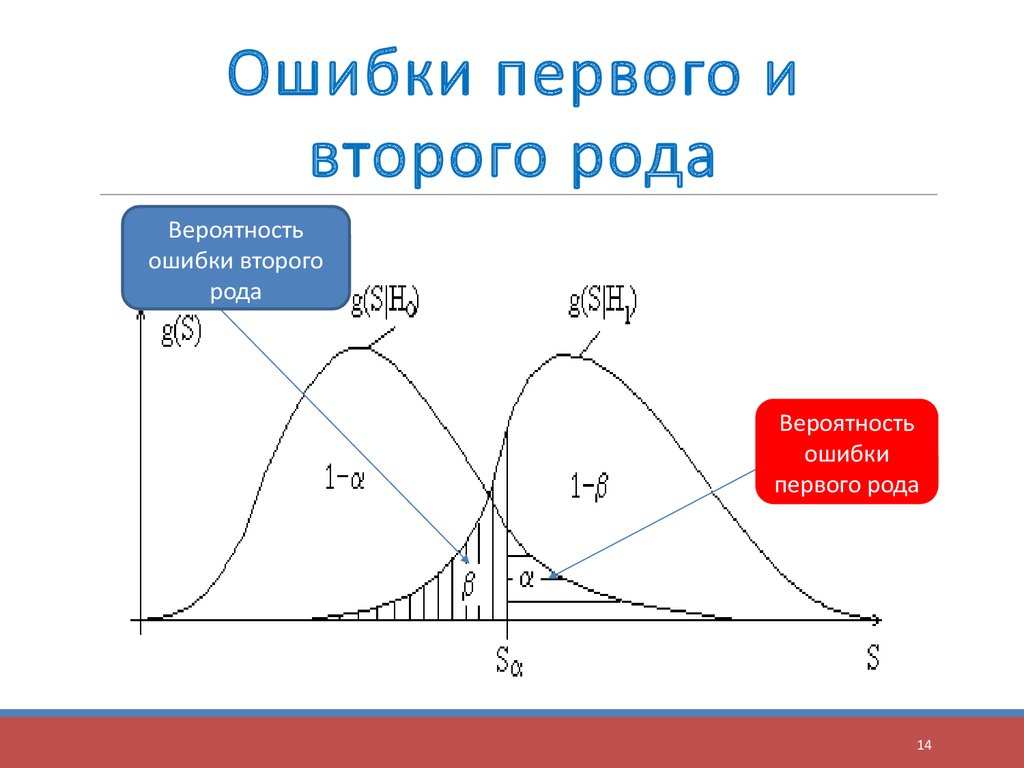
14.
Ошибки первого ивторого рода
Вероятность
ошибки второго
рода
Вероятность
ошибки
первого рода
14
15.
Этапы проверки гипотезы опараметрах распределения
1. формулируются гипотезы
Н0 и Н1;
2. задается уровень значимости α;
3. выбирается статистика Z критерия для проверки Н0;
определяется выборочное распределение статистики Z
при условии, что верна Н0;
4. в зависимости от Н1 определяется критическая
область;
5. вычисляется выборочное значение статистики z;
6. принимается статистическое решение.
15
16.
Статистическое решениеЕсли zв принадлежит критической области
Отклонить гипотезу Н0 как несогласующуюся с
результатами наблюдений
Если zв не принадлежит критической
области
Принять гипотезу Н0, т.е. считать, что она не
противоречит результатам наблюдений
16
17.
Замечания1. На этапах 4-7 используют статистику, квантили
которой табулированы.
2. В статистических пакетах обычно не используется
значения задаваемого уровня значимости. В выходных
данных содержатся выборочные значения статистики
критерия и вероятность того, что с.в. превышает
выборочное значение.
Эта вероятность называется р-значением (p-level).
17
18.
математическаястатистика / под ред. А.В.
Ефимова.
По паспортным данным автомобильного двигателя расход
топлива на 100 км. пробега составляет 10л. В результате изменения
конструкции двигателя ожидается, что расход топлива уменьшится.
Для проверки проводятся испытания 25 случайно отобранных
автомобилей с модернизированным двигателем, причем
выборочное среднее расходов топлива на 100 км. пробега по
результатам испытаний составило 9,3 л. Предположим, что выборка
расходов топлива получена из нормально распределенной
генеральной совокупности со средним а и дисперсией 4 л 2 .
Используя
критерий
значимости,
проверить
гипотезу,
утверждающую, что изменение конструкции двигателя не повлияло
на расход топлива.
18
19.
Пример 2◦ В условиях примера 1 предположим, что
наряду с гипотезой Н0 :а=10л рассматривается
альтернативная гипотеза Н1 :а=9л. В качестве
статистики критерия рассмотрим выборочное
среднее
Предположим, что критическая
область задана неравенством 9,44л. Найти
вероятности ошибок первого и второго рода
для критерия с такой критической областью.
19
20.
Критерии согласияПусть х1 , х2 ….. хn– выборка наблюдений случайной величины X.
Проверяется гипотеза Н0 о том, что случайная
величина X имеет функцию распределения
F(x).
◦ 1. По выборке наблюдений находят оценки неизвестных
параметров предполагаемого закона распределения с.в. Х.
◦ 2. Область возможных значений с.в. Х разбивается на r множеств
Δ1, Δ2,… Δr . Если Х-непрерывная с.в., то на r интервалов, если Хдискретная с.в., то r-число групп.
◦ 3. Подсчитывается число элементов выборки - nk,
принадлежащих множеству Δк , к=1,2, ….r.
=n.
20
21.
Критерий4. Используя предполагаемый закон
распределения с.в. Х, находят
вероятности pk =P[X Δк ], к=1,2, ….r.
Очевидно, что =1.
5. Выборочное значение статистики
критерия вычисляется по формуле
21
22.
Критерий6. Гипотеза Н0 согласуется с результатами
наблюдений на уровне значимости , если <(r-l-1),
где (r-l-1) – квантиль порядка 1-α распределения с
(r-l-1) степенями свободы, l – число неизвестных
параметров распределения, оцениваемых по
выборке.
Необходимо, чтобы для всех
интервалов выполнялось условие 5.
Если для некоторых интервалов это условие не
выполняется, то их следует объединить с
соседними.
22
23.
Проверить гипотезу:Н 0 : а = а 0, где а 0 = +0,5s
23
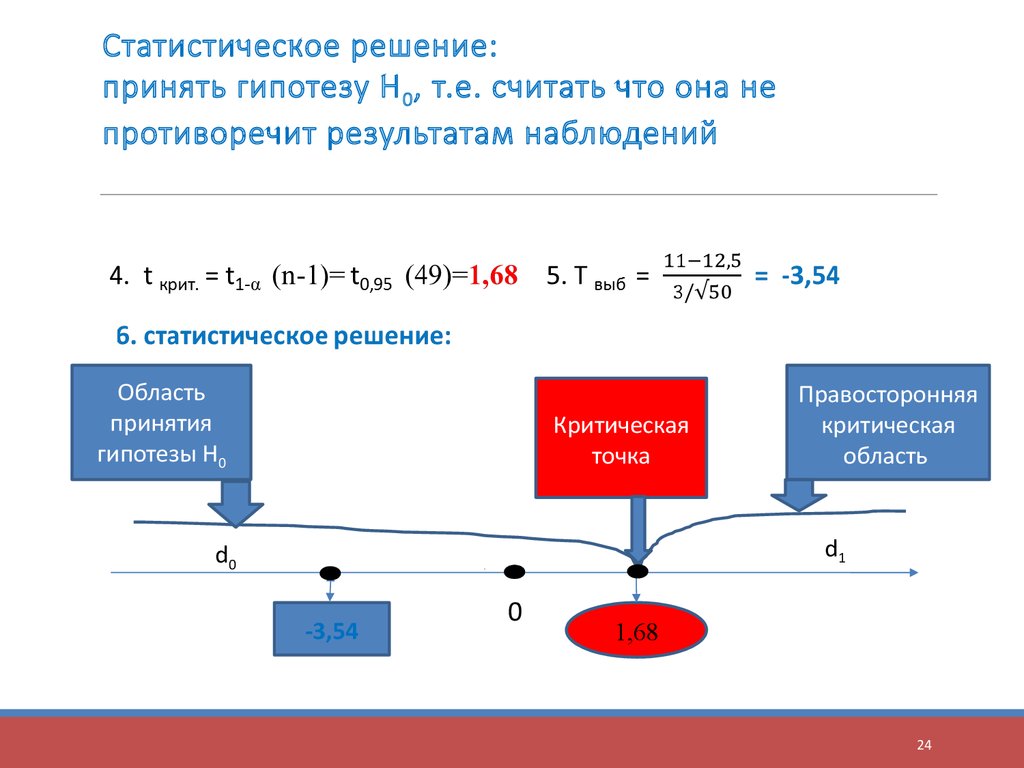
24.
Статистическое решение:принять гипотезу Н 0, т.е. считать что она не
противоречит результатам наблюдений
Область
принятия
гипотезы Н0
Критическая
точка
Правосторонняя
критическая
область
d1
d0
-3,54
0
1,68
24
25.
Н 0 : = ϭ02 , где ϭ02 = 3sСтатистическое решение:
принять гипотезу Н0, т.е.
считать что она не
противоречит результатам
наблюдений
d1
d0
32,4
d1
71,4
25
26.
КритерийОбъем выборки n=50.
Оценка математического ожидания =11
Оценка дисперсии S2 = 8,82 S=2,97
1. Н 0 : Х распределена по нормальному з
2. уровень значимости α=0,05
3.
26
27.
p k =P[X Δ к ]=Ф()-Ф()Номер
интервала
Границы
интервалов
1
1
2
2
--6
6
6 -- 8
8
8
8 -- 10
10
10 - 12
12 - 14
14 - 16
16 -
3
3
4
5
6
7
-
-- 1,67
1,67
-- 1
1
-- 1,67
1,67
-- 1
1
-- 0,33
0,33
0,33
- 0,33
0,33
1
1,67
1
1,67
+
Φ(
Φ(
-- 0,5
0,5
-- 0,4525
0,4525
-- 0,4525
0,4525
-- 0,3413
0,3413
-- 0,3413
0,3413
- 0,1293
0,1293
0 ,3413
0, 4525
-- 0,1293
0,1293
0,1293
0,0475
0,0475
0,1112
0,1112
0,212
0,212
0,2586
0 ,3413
0,212
0, 4525
0 ,5
0,1112
0,0475
1
27
28.
Выборочное значение статистикикритерия
Номер
интервала
1
2
3
4
5
6
7
Наблюдаемая частота
nk
2
7
9
13
11
6
2
50
Ожидаемая
частота
n
nk - n
0,0475
2,375
0,1112
5,56
7,935
1,065
0,143
0,212
10,6
10,6
-1,6
0,242
0,2586
12,93
12,93
0,07
0,000
0,212
10,6
10,6
0,4
0,015
0,1112
5,56
7,935
0,065
0,001
0,0475
2,375
1
50
0,401
28
29.
Статистическое решениеГипотеза Н0 согласуется с результатами наблюдений на уровне
значимости , если <(r-l-1),
где (r-l-1) – квантиль порядка 1-α распределения с (r-l-1)
степенями свободы, l – число неизвестных параметров
распределения, оцениваемых по выборке.
r=5; l=2
Число степеней свободы r-l-1 = 5-2-1=2
(r-l-1)= (2) =(2)=5,99
= 0,401
Гипотеза о нормальном
распределении выборки
согласуется с результатами
наблюдений
29


























 mathematics
mathematics








