Проверка статистических гипотез. Урок № 34

1.

Проверка
статистических гипотез
Урок № 34

2.

В экономике, производстве и различных
областях науки и техники часто для выяснения
истинности того или иного случайного факта
прибегают к проверке тех или иных
предположений или высказываний, которые
называют гипотезами.
Опираясь на результаты наблюдений в
случайной выборке, гипотезы можно проверить
статистически, используя критерии оценки
статистических гипотез.

3.

Определение.
Под статистическими гипотезами
подразумеваются такие гипотезы,
которые относятся или к виду случайной
величины, или к отдельным параметрам
распределения случайной величины.

4.

К статистическим гипотезам
можно отнести высказывания
типа
случайная величина X подчиняется
нормальному закону распределения
генеральные средние двух исследуемых
совокупностей равны между собой

5.

Средние размеры одежды, производимые
на однотипных предприятиях, не
различаются между собой.
Распределение трудовых ресурсов в
одинаковых организационно-технических
условиях имеет нормальный закон
распределения.

6.

Выдвинутую гипотезу называют нулевой и
обозначают Н0.
ПО отношению к высказанной (основной)
нулевой гипотезе всегда можно
сформулировать альтернативную или
конкурирующую гипотезу,
противоречащую ей - H1.

7.

Определение.
Проверкой статистических гипотез
называется сопоставление выдвинутой
гипотезы Н0 с альтернативной при
использовании статистических
критериев и данных выборочных
наблюдений.

8.

Определение.
Если гипотеза H0 сводится к
утверждению, что значение некоторого
неизвестного параметра распределения
случайной величины равно заданной
величине, то гипотеза называется
простой.

9.

Критическая область
и область допустимых значений
Все возможное множество выборок
объема n можно разделить на два
непересекающихся подмножества
(обозначим их через О и W), таких, что
проверяемая гипотеза Н0 должна быть
отвергнута, если наблюдаемая выборка
попадет в подмножество W, и принята,
если выборка принадлежит
подмножеству О.

10.

Определение.
Подмножество W выборок таких, что
проверяемая гипотеза Н0 должна быть
отвергнута, называют критической
областью;
Подмножество О выборок таких, что
проверяемая гипотеза Н0 должна быть
принята,— областью допустимых
значений.

11.

Так как подмножество О состоит из всех
тех выборок, которые не вошли в
подмножество W, то подмножество W
однозначно определяет подмножество
О, и наоборот.
Т.е. необходимо определить одно
подмножество, второе же получается
автоматически единственным образом.

12.

Возникает вопрос о том, какими
принципами следует руководствоваться
при построении критической области W.
Эти принципы были сформулированы в
работах известных математиков Е.
Неймана и Э. Пирсона.

13.

При выборе критической области
следует иметь в виду, что принимая или
отклоняя гипотезу Н0, можно допустить
ошибки двух видов:
ошибки 1-го рода
ошибки 2-го рода

14.

Ошибки двух видов
Ошибка первого рода состоит в том,
что нулевая гипотеза Н0 отвергается,
т.е. принимается гипотеза H1 в то время
как в действительности все же верна
гипотеза Н0.
Ошибка второго рода состоит в том,
что гипотеза Н0 принимается, в то время
как верна гипотеза H1

15.

Ошибки двух видов
Гипотеза Н0
Отвергается
Верна
Неверна
Ошибка 1-го Правильное
рода
решение
Принимается Правильное
решение
Ошибка 2-го
рода

16.

Методы оценки
статистических гипотез
Проверка статистических гипотез
осуществляется с помощью выбранного
статистического критерия.

17.

Статистическим критерием называют
правило, которое позволяет оценить
меру расхождения результатов,
полученных при оценке выборочного
наблюдения и основной выдвинутой
гипотезы Н0

18.

Статистический критерий подбирается в
каждом отдельном случае таким
образом, чтобы он соответствовал
принципу отношения правдоподобия.

19.

Критерий К с известной функцией
плотности f(k) позволяет при
заданном уровне значимости
определить критическую точку Ккр.
распределения f(k).
Обычно Ккр. определяется по таблице
соответствующего распределения.

20.

Ккр. разделяет область значений критерия
на две части:
область допустимых значений, в которой
результаты выборочного исследования
выглядят более правдоподобно,
и критическую область, в которой
результаты выборочного наблюдения
менее правдоподобны в отношении
гипотезы H0.

21.

Значение критерия на основе
выборочного наблюдения
определяется по специальным
правилам и называется наблюдаемым
значением критерия Кнабл.

22.

Если наблюдаемое значение критерия
попадает в область допустимых
значений О, значит, на основе
выборочных данных на принятом
уровне значимости можно принять
нулевую гипотезу Н0 как более
правдоподобную для результатов
выборочного исследования.

23.

Если же наблюдаемое значение
критерия попадает в критическую
область W, то нулевая гипотеза
отклоняется в пользу альтернативной
гипотезы Н1

24.

Критическая область может быть
односторонней (левосторонней и
правосторонней) или двухсторонней в
зависимости от того как задана
конкурирующая гипотеза H1

25.

В том случае, когда конкурирующая
гипотеза H1 —правосторонняя, то и
критическая область — правосторонняя
Тогда, если Кна6л попадает в интервал от
-∞ до Ккр , то нулевая гипотеза
принимается, а альтернативная
отклоняется.
Если же Кна6л > К , то нулевая гипотеза
отклоняется в пользу альтернативной.

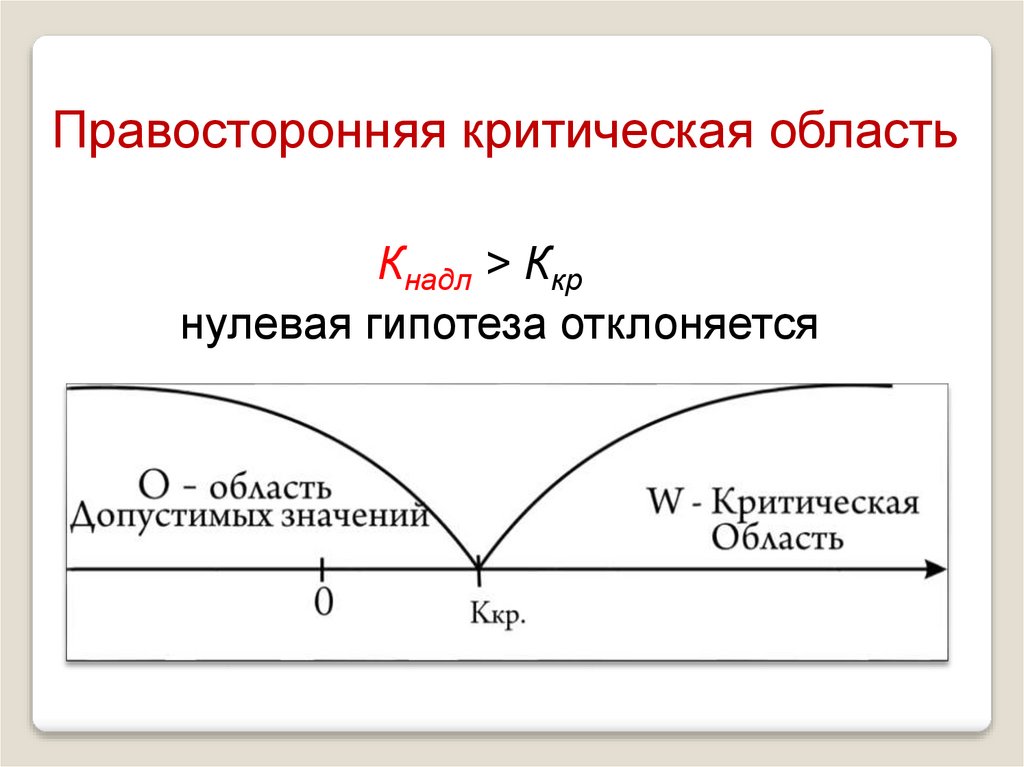
26.

Правосторонняя критическая область
Кнадл > Ккр
нулевая гипотеза отклоняется

27.

В том случае, когда конкурирующая
гипотеза Н1 левосторонняя, то и
критическая область левосторонняя
Тогда, если Кнабл. лежит в интервале от
- ∞ до Ккр. , то нулевая гипотеза
отклоняется в пользу альтернативной.
Если же Кнадл > Ккр. , то нулевая
гипотеза принимается, а альтернативная
отклоняется.

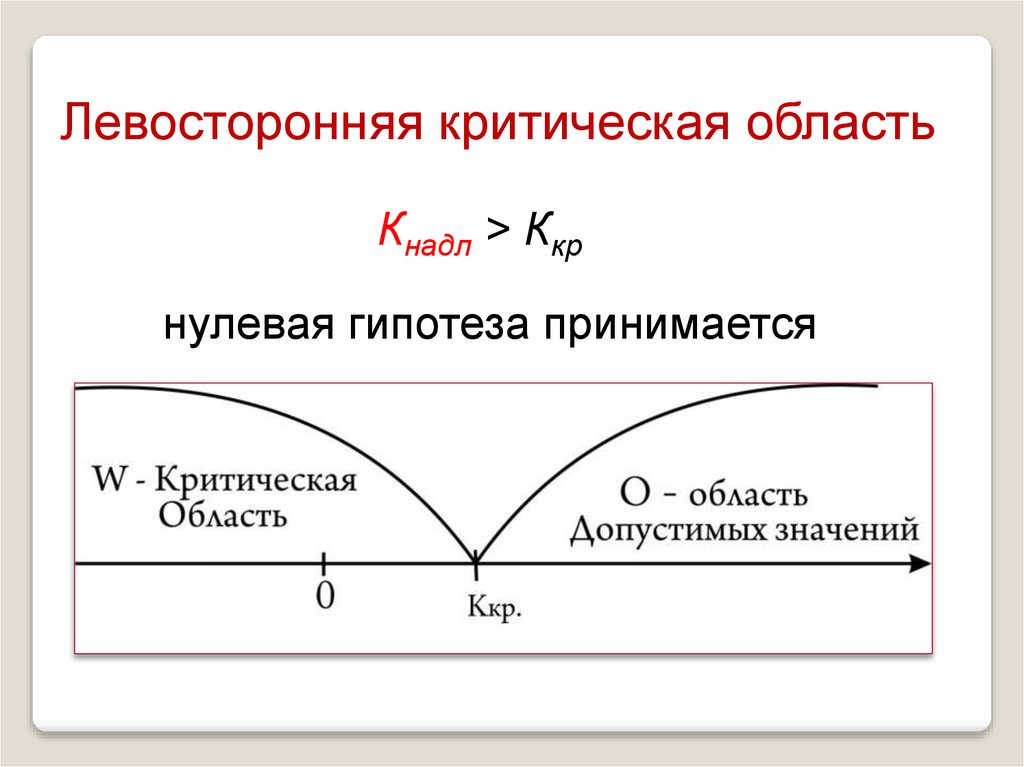
28.

Левосторонняя критическая область
Кнадл > Ккр
нулевая гипотеза принимается

29.

Если конкурирующая гипотеза Н1
двухсторонняя, то и критическая
область, двухсторонняя .
Тогда нулевая гипотеза принимается,
если
-Ккр. < Кнабл. < Ккр. ,
и отклоняется в противном случае в
пользу альтернативной.

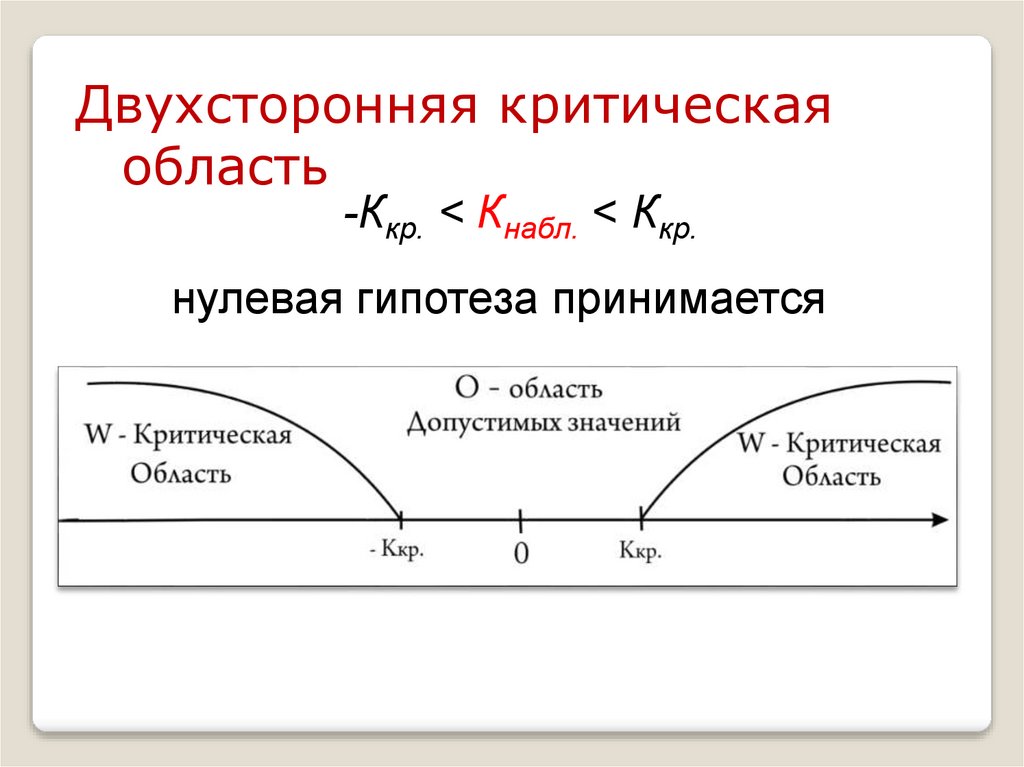
30.

Двухсторонняя критическая
область
-Ккр. < Кнабл. < Ккр.
нулевая гипотеза принимается

31.

Проверка выдвинутого в процессе
анализа или исследования
предположения выполняется
обычно по следующему плану:
1) Выдвигается нулевая гипотеза Н0;
2) Формулируется альтернативная
гипотеза Н1;
3) Задается уровень значимости а,
удовлетворяющий исследователя;

32.

4) Подбирается наиболее мощный
критерий оценки гипотезы по
статистическим данным.
Чаще всего это:
n — нормальное распределение;
χ2 — распределение Пирсона хи-квадрат;
t — распределение Стьюдента;
5) Вычисляется экспериментальное
значение критерия на основе
выборочных данных;

33.

6) Определяется табличное значение
критерия. В зависимости от вида
альтернативной гипотезы в
соответствующей таблице выбирают
квантили критерия для двусторонней
(К1-a/2 И Кa/2 ) или односторонней
области (К1-а или Ка);
7) Табличное значение критерия
определяет точку Ккр , которая
отделяет критическую область W OT
области допустимых значений;

34.

8) Если значение Кнабл. находится в
области допустимых значений О, то на
уровне значимости а нулевая гипотеза
принимается, а конкурирующая
отклоняется;
9) Если вычисленное по выборочным
данным значение Кнабл попадает в
критическую область, то нулевая
гипотеза отклоняется в пользу
конкурирующей гипотезы.

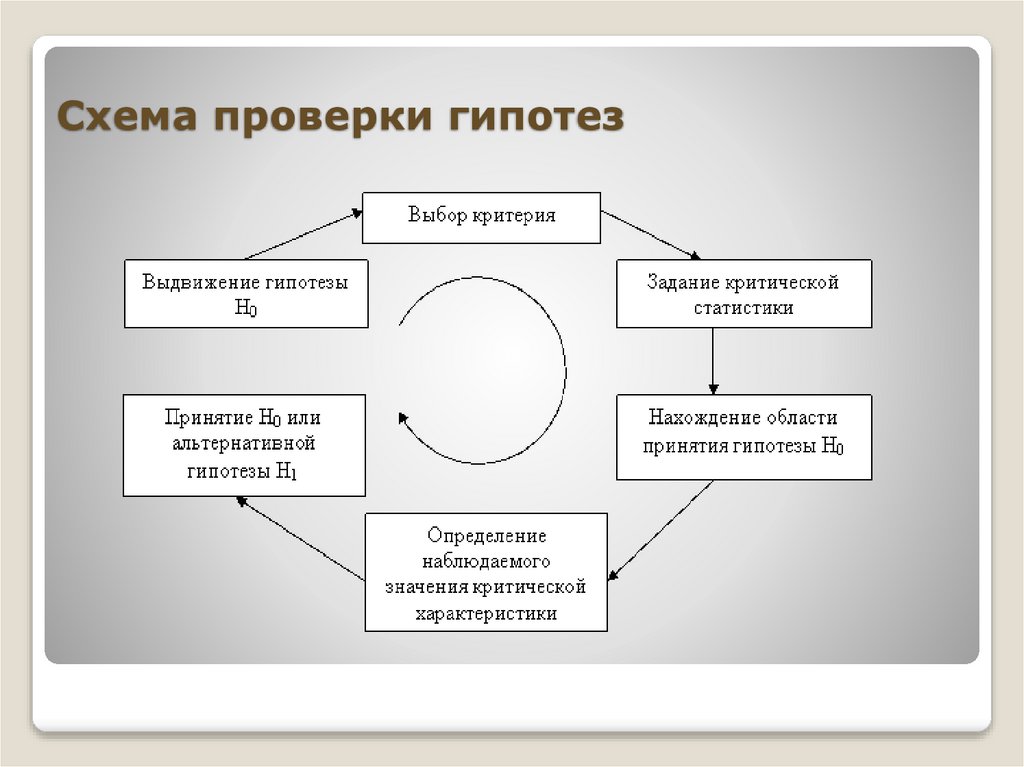
35.

Схема решения задачи
Этапы проверки
статистических гипотез

36.

Располагая
выборочными данными
Х 1, Х 2 , ... , Х n и руководствуясь
конкретными условиями задачи,
формулируют гипотезу H0, которую
называют основной или нулевой, и
гипотезу H1,
конкурирующую с
гипотезой H0.
Первый этап

37.

Задаются вероятностью α («альфа»),
которую называют уровнем значимости.
α = PH0 (H1)
где PH0(H1) – вероятность того, что
будет принята гипотеза H1, если на
самом деле в генеральной совокупности
верна гипотеза H0.
α – вероятность ошибки первого рода
Второй этап

38.

Вероятность α задается заранее,
разумеется, малым числом, поскольку
это вероятность ошибочного значения:
0,05; 0,01; 0,005; 0,001.
Например, α = 0,05 означает
следующее: если гипотезу H0
проверять по каждой из 100 выборок
одинакового объема, то в среднем в 5
случаях из 100 мы совершим ошибку
первого рода.

39.

Находят величину φ такую, что:
ее значения зависят от выборочных
данных Х 1, Х 2 , ... , Х n,
т.е. для которой справедливо
равенство
φ = φ (Х 1, Х 2 , ... , Х n);
Величину φ
называют критерием.
Третий этап

40.

Так как значения критерия позволяют
судить о «расхождении выборки с
гипотезой H0», то из области
допустимых значений критерия φ
следует выделить подобласть ω таких
значений, которых свидетельствовали
бы о существенном расхождении
выборки с гипотезой H0 и,
следовательно, о невозможности
принять гипотезу H0. подобласть ω
называют критической областью.
Находят φ кр.
Четвертый этап

41.

В формулу критерия
φ = φ (Х 1, Х 2 , ... , Х n) вместо
Х 1, Х 2 , ... , Х n подставляют
конкретные числа, полученные в
результате n наблюдений.
Подсчитывают числовое значение
φчис. = φ набл. критерия.
Пятый этап

42.

Делают вывод
Если φ набл. критерия попадает в область
допустимых значений, то принимают
основную гипотезу.
Если φ набл. критерия попадает в
критическую область, то принимают
конкурирующую гипотезу.
Шестой этап

43.

Схема проверки гипотез

44.

Решение задач

45.

Экстрасенсу предложили подтвердить
диагноз 16 человек, в 10 из ответов был
поставлен правильный диагноз.
На уровне значимости 0,05 определите,
случайно ли это, или целитель
действительно обладает
экстрасенсорными способностями?
Задача 1

46.

Сформулируем нулевую и
конкурирующую гипотезы.
H0: Х~ R(a; b) — случайная величина X
подчиняется равномерному
распределению с параметрами (а; Ь), то
есть правильные диагнозы установлены
случайно (ттеор = тэкспер)
Первый этап

47.

Н1: случайная величина X не
подчиняется равномерному
распределению, то есть распределение
числа правильных диагнозов не
случайно и целитель действительно
обладает экстрасенсорными
способностями (ттеор < тэкспер).
Альтернативная гипотеза Н1
правосторонняя, значит и критическая
область правосторонняя.
Первый этап

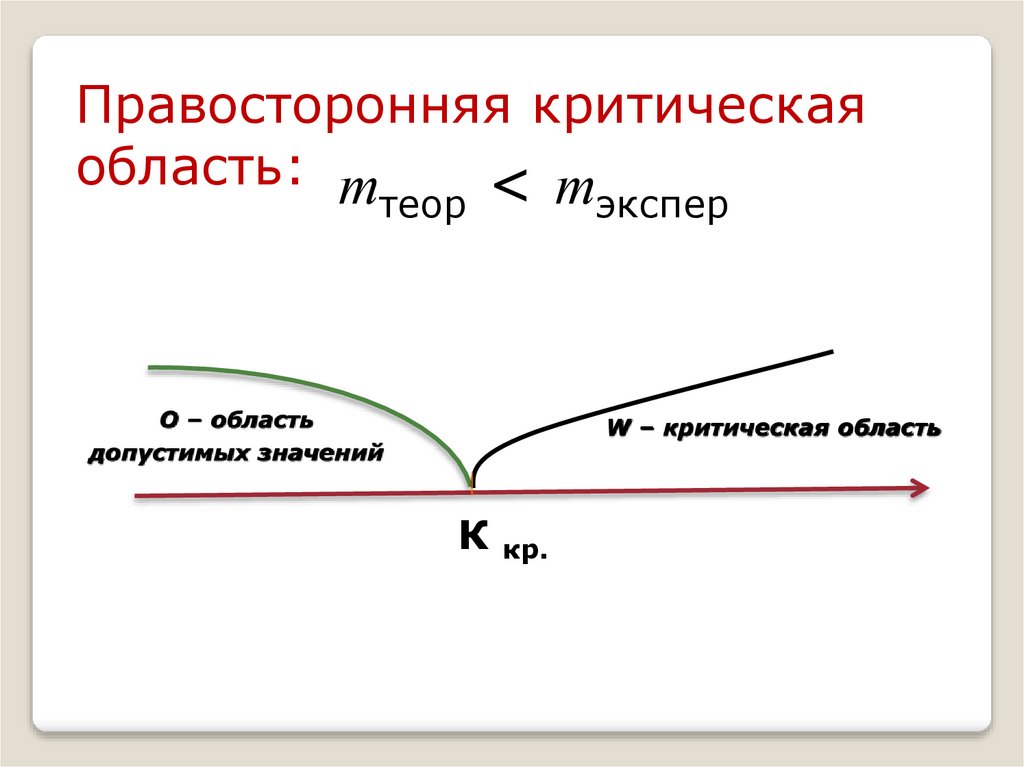
48.

Правосторонняя критическая
область: т
<т
теор
О – область
допустимых значений
экспер
W – критическая область
К кр.

49.

Задать уровень значимости.
Он дан в условии задачи.
По условию α = 0,05
Второй этап

50.

Этот вид статистических гипотез относится
к гипотезам о виде закона распределения
генеральной совокупности.
В качестве критерия для проверки
статистических гипотез о неизвестном
законе распределения генеральной
совокупности используется критерий
Пирсона, случайная величина χ2 (хиквадрат).
Выбор критерия

51.

Критическое значение следует определять
по таблице распределения (χ2набл.) по
уровню значимости α и числу степеней
свободы k.
Число степеней свободы рассчитывается по
формуле:
k=n–l-1
где k — число степеней свободы
n – число групп выборки;
l — число неизвестных параметров
предполагаемой модели, оцениваемых по
данным выборки (если все параметры
предполагаемого закона известны точно,
то l = 0).

52.

По условию задачи число групп
выборки (n) равно 2, так как могут быть
только два варианта ответов
экстрасенса: верные и неверные.
Число неизвестных параметров
равномерного распределения (l ) равно
0.
Отсюда, k = 2-0-1 = 1.

53.

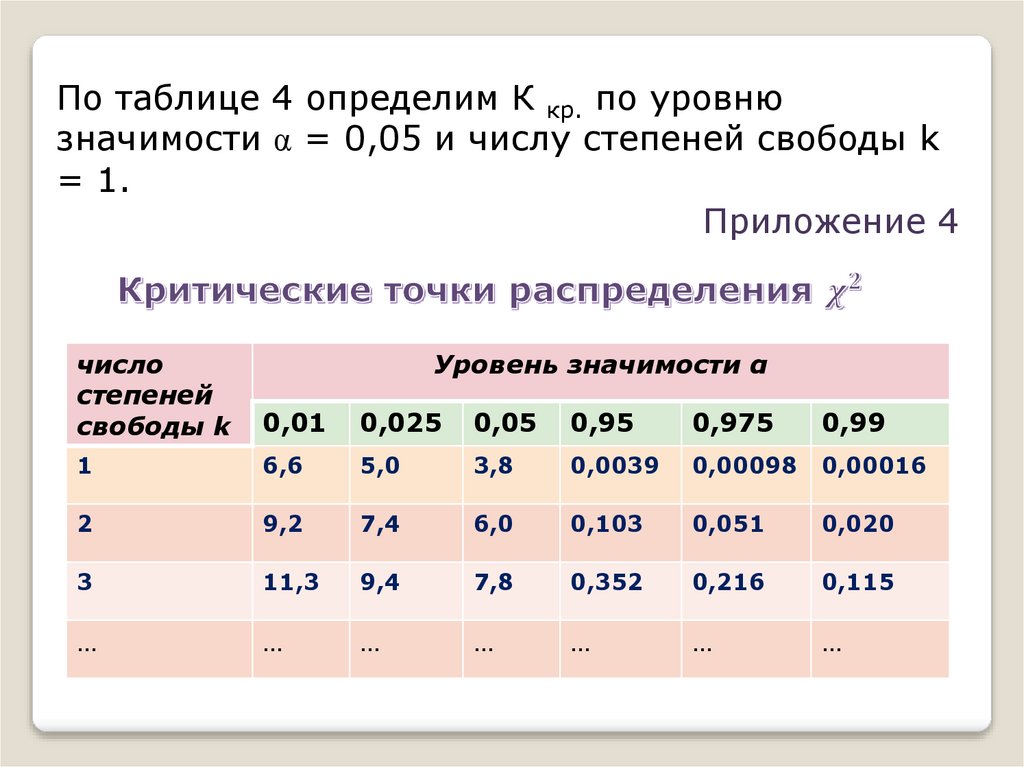
По таблице определим χ2кр.
по уровню значимости α = 0,05
по числу степеней свободы k = 1
Получим
К кр. = χ2кр.(α = 0,05; k = 1) = 3,8
Третий этап

54.

По таблице 4 определим К кр. по уровню
значимости α = 0,05 и числу степеней свободы k
= 1.
Приложение 4
число
степеней
свободы k
Уровень значимости α
0,01
0,025
0,05
0,95
0,975
0,99
1
6,6
5,0
3,8
0,0039
0,00098
0,00016
2
9,2
7,4
6,0
0,103
0,051
0,020
3
11,3
9,4
7,8
0,352
0,216
0,115
…
…
…
…
…
…
…

55.

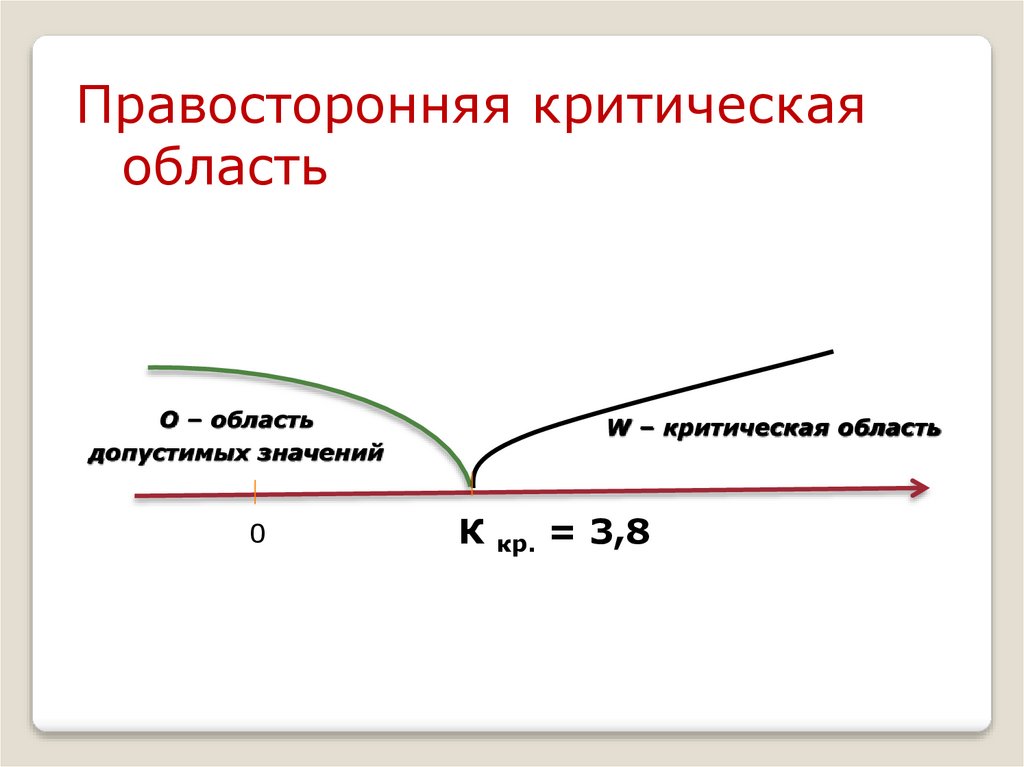
Правосторонняя критическая
область
О – область
допустимых значений
0
W – критическая область
К кр. = 3,8

56.

Наблюдаемое значение (χ2набл.)
рассчитывается по формуле:
2
набл.
где т(эмп)i
n
(т( эмпир)i т( теор)i )
i 1
т( теор)i
2
эмпирическая частота i-той
группы выборки;
т (теор)i теоретическая частота i-той
группы выборки.

57.

Для того чтобы ответить на вопрос
задачи, проверим статистическую
гипотезу о том, совпадает ли данное
эмпирическое распределение числа
действий экстрасенса с равномерным
теоретическим распределением, при
котором вероятность выбрать
правильное решение – ½ ?

58.

Если ответ экстрасенса выбираются
случайно, то, с учетом особенностей
равномерного распределения, число
правильных и неправильных ответов
должно распределиться поровну,
значит, в этом случае 8 ответов
должны быть правильными, а 8 нет.
Четвертый этап

59.

Составим таблицу распределения
эмпирических и теоретических частот:
Частоты
эмпирическая
теоретическая
Число
Число
правильных неверных
ответов
ответов
10
8
6
8
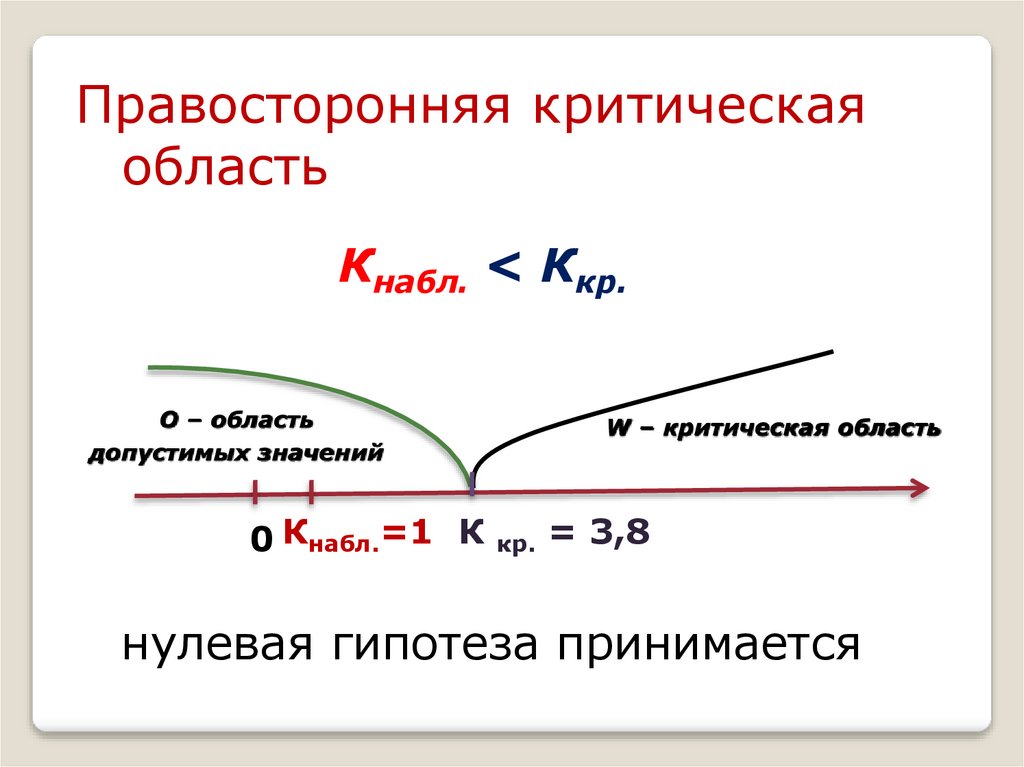
Найдем наблюдаемое значение χ2набл.:
K набл= χ2набл.=(10 – 8)2 / 8 + (6 – 8)2 / 8 = 1

60.

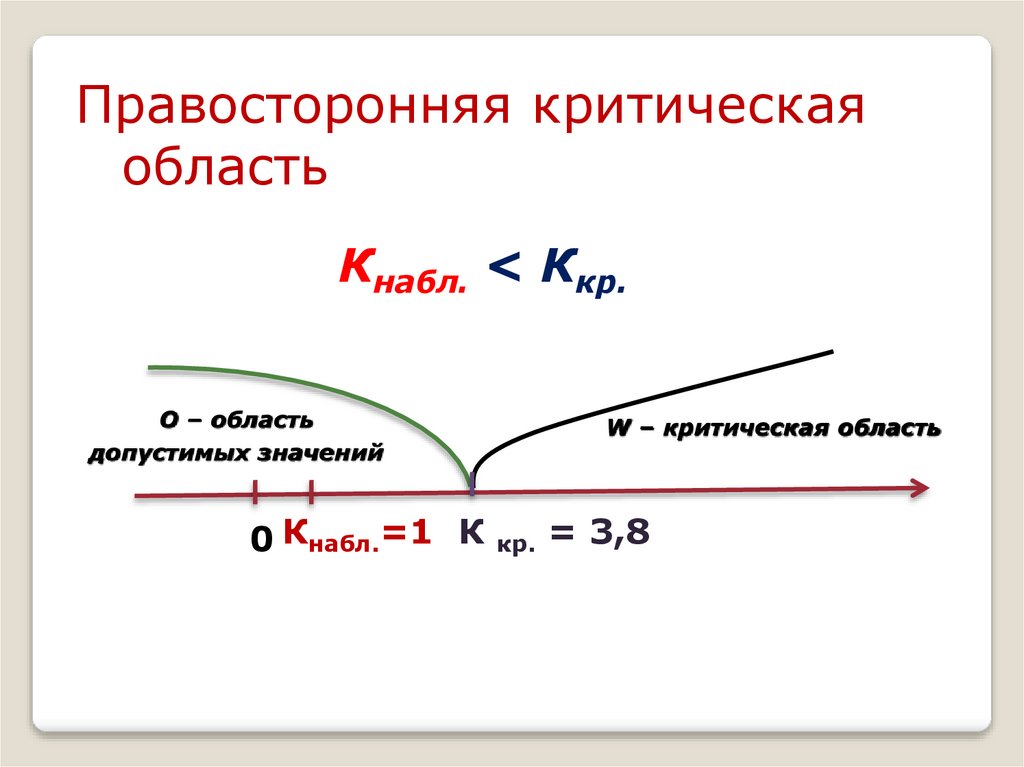
Правосторонняя критическая
область
Кнабл. < Ккр.
О – область
допустимых значений
W – критическая область
0 Кнабл.=1 К кр. = 3,8

61.

χ2набл.< χ2кр. лежит в области О,
следовательно, на данном уровне
значимости нулевую гипотезу нельзя
отклонить, расхождения эмпирических
и теоретических частот незначимые.
Данные наблюдений согласуются с
гипотезой о равномерном
распределении генеральной
совокупности.
Пятый этап

62.

Правосторонняя критическая
область
Кнабл. < Ккр.
О – область
допустимых значений
W – критическая область
0 Кнабл.=1 К кр. = 3,8
нулевая гипотеза принимается

63.

Это означает, что на уровне значимости
α = 0,05 можно утверждать, что
правильные диагнозы установлены
случайно и целитель не обладает
экстрасенсорными способностями.
Ответ: на уровне значимости α = 0,05
можно утверждать, что целитель не
обладает экстрасенсорными
способностями.

64.

Вопросы для самоконтроля
Что подразумевают
под статическими
гипотезами?
В чем состоит смысл ошибок второго рода ?
Какую гипотезу обозначают Н0 ?
Как обозначают альтернативную гипотезу?
Перечислить этапы проверки гипотезы
Виды критических областей и критерии
принятия гипотез

65.

Данный
критерий
был
разработан
Уильямом Госсеттом для оценки качества
пива в компании Гинесс . В связи с
обязательствами перед компанией по
неразглашению
коммерческой тайны (а
руководство Гиннесса считало таковой
использование статистического аппарата в
своей работе), статья Госсетта вышла в
журнале «Биометрика» под псевдонимом
«Student» (Студент).