Similar presentations:
Основы теории проверки статистических гипотез
1. Основы теории проверки статистических гипотез.
2.
Процедура сопоставления высказанногопредположения (гипотезы) с выборочными
данными называется проверкой гипотез.
Задачи статистической проверки гипотез:
Относительно
некоторой
генеральной
совокупности высказывается та или иная
гипотеза Н0.
Из этой генеральной совокупности извлекается
выборка.
Требуется указать правило, при помощи
которого можно было бы по выборке решить
вопрос о том, следует ли отклонить гипотезу Н0
или принять ее.
3.
Гипотеза – предположение о свойствепопуляции (каком-либо параметре, форме
распределения…).
Тестирование гипотезы (hypothesis testing) – –
процедура, в которой мы решаем, принять
гипотезу («accept») или отвергнуть (reject).
Примечание. На самом деле мы никогда не можем действительно принять гипотезу: можем либо
отвергнуть, либо не иметь достаточных оснований, чтобы её отвергнуть.
4.
Предполагается, что мыформулируем гипотезу ДО сбора
данных.
5.
Тестирование гипотез в статистикеГипотеза формулируется о свойствах ПОПУЛЯЦИИ =
генеральной совокупности, (предположения о самой выборке
легко проверить без статистики).
Опровергнуть гипотезу в принципе легче, чем подтвердить.
Формулируем ДВЕ взаимоисключающие гипотезы:
H0 (нулевая гипотеза, null hypothesis) – её мы собираемся опровергать; обычно
говорит, что нет различий, нет эффекта, нет изменений…
H1 (альтернативная гипотеза, alternative hypothesis) – её мы примем, если
удастся отвергнуть H0 .
Решение о том, принять или отвергнуть гипотезу
принимается на основе статистики критерия (test statistic).
6.
7.
Уровнем значимости критерия ( ) называетсявероятность допустить ошибку 1-го рода.
Уровень значимости — процент появления ошибок
первого рода (отклонение верной нулевой гипотезы).
• первый уровень — 5% или 0.05, т. е. вероятность
ошибиться 5 к 100 или 1 к 20.
• второй уровень — 1% или 0.01, т. е. вероятность 1 к 100.
• третий уровень — 0.1% или 0.001, вероятность 1 к 1000.
8.
Тестирование гипотез в статистикеХорошая практика при изложении результатов в
публикации –
Приводить точную оценку вероятности ошибки 1-го рода p
(например, р=0.025, р=0.0001). Тогда читатель может сам
выбирать уровень значимости.
* - достоверные различия – р<0.05
** - высокодостоверные различия - р<0.01
*** - р<0.001
Если вероятность ошибки близка к α, лучше всего провести
дополнительные исследования и не делать окончательных
выводов (Zar, 2010)
9.
Тестирование гипотез в статистикеОдновыборочные критерии
сравнивающие среднее значение с заданным числом.
Двусторонняя
альтернатива
(two-tailed
hypothesis)
H0: μ = 90 г;
H1 : μ ≠ 90 г
Односторонняя
альтернатива
(one-tailed
hypothesis)
H0: μ ≤ 90 г;
H1 : μ > 90 г
10. Сравнение групп
11.
Виды критериевПараметрические т.е. основанные на расчете параметрв
генеральной совокупности (X, σ2).
Достоинства:
• более мощные и точные.
Трудности:
• требуют измерений по шкале интервалов или равных отношений;
• только нормальное распределение!;
• желательный объем выборки N>50
12.
t-критерий Стьюдента - общее название для классаметодов статистической проверки гипотез (статистических
критериев), основанных на распределении Стьюдента.
Наиболее частые случаи применения t-критерия связаны с
проверкой равенства средних значений в двух выборках.
13.
Применение tкритерияКритерий позволяет
найти вероятность того,
что оба средних значения в
выборке относятся к одной
и той же совокупности.
Данный критерий
наиболее часто
используется для проверки
гипотезы: «Средние двух
выборок относятся к одной
и той же совокупности».
При использовании критерия можно
выделить два случая.
В первом случае его применяют для проверки
гипотезы о равенстве генеральных средних двух
независимых, несвязанных выборок (так
называемый двухвыборочный t-критерий). В этом
случае есть контрольная группа и
экспериментальная (опытная) группа, количество
испытуемых в группах может быть различно.
Во втором случае, когда одна и та же группа
объектов порождает числовой материал для
проверки гипотез о средних, используется так
называемый парный t-критерий. Выборки при
этом называют зависимыми, связанными.
14.
Критерий Стьюдента применяется, еслинужно сравнить только две группы
количественных признаков с
нормальным распределением (частный
случай дисперсионного анализа).
Примечание: этим критерием нельзя
пользоваться, сравнивая попарно
несколько групп, в этом случае
необходимо применять дисперсионный
анализ.
15.
16.
17.
18.
Виды критериевНепараметрические т.е. не включающие в
формулу расчета параметров распределения,
основанные на оперировании частотами или
рангами.
Достоинства:
• просты в расчете;
• применимы на малых выборках (N<10);
• не привязаны к характеру распределения.
Недостатки:
• менее мощные (β),
• имеют табличные ограничения по макс. N
19.
20.
Критерий Вилкоксона - вычисляются разности между индивидуальнымизначениями показателя после проведения эксперимента и до него.
Алгоритм проверки:
1. Модули разностей ранжируются в порядке возрастания.
2. Отмечаются ранги, соответствующие сдвигам в нетипичном направлении.
Например, если в большинстве случаев после проведения эксперимента
наблюдалось увеличение измеряемого параметра, то его уменьшение следует
считать нетипичным сдвигом.
3. Эмпирическое значение критерия определяется как сумма рангов,
соответствующих нетипичным сдвигам.
4. Если критическое значение не превосходит эмпирического, то на данном уровне
значимости отсутствуют основания для отклонения нулевой гипотезы о
несущественности различий. В противном случае нулевая гипотеза отвергается.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44. КОРРЕЛЯЦИОННЫЙ и РЕГРЕССИОННЫЙ АНАЛИЗ
45.
Если из множества значенийаргумента Х одному значению
соответствуют множество значений
Y на конечном интервале значений,
то такая взаимосвязь называется
корреляционной.
46. Различают корреляции нескольких направлений:
Прямая положительная корреляция, прикоторой увеличение причинного фактора
вызывает увеличение следственного
фактора; например, увеличение силы мышц
разгибателей ног положительно сказывается
на росте результатов в прыжках в высоту с
разбега.
47.
Прямая отрицательная корреляция, прикоторой уменьшение причинного
фактора вызывает уменьшение
следственного фактора; например,
уменьшение длины дистанции
приводит к сокращению времени её
преодоления.
48.
Обратная положительная корреляция,при которой уменьшение причинного
фактора вызывает увеличение
следственного фактора; например,
уменьшение длины дистанции
приводит к увеличению скорости бега.
49.
Обратная отрицательная корреляция,при которой увеличение причинного
фактора вызывает уменьшение
следственного; например, увеличение
силы мышц может привести к
уменьшению скорости их сокращения.
50. Коэффициент корреляции
(r)–показатель тесноты взаимосвязи
между парой показателей,
получивший широкое применение в
практике.
51.
Количественную меру коэффициентакорреляции принято различать по
нескольким уровням:
Слабая связь – при /r/ < /0,30/
Средняя связь – при /0,31/ < /r/ < /0,69/
Сильная связь – при /0,70/ < /r/ < /0,99/
52.
Качественный анализ коэффициентакорреляции принято различать по
характеру взаимосвязи:
Отрицательная связь – при r < 0
Положительная связь – 0 < r
При r=0 – взаимосвязь отсутствует.
53. Результат вычисления коэффициента корреляции позволяет отвечать на три вопроса:
Имеется ли взаимосвязь междудвумя величинами?
Какова направленность этой
взаимосвязи (прямо или обратно
пропорциональная)?
Какова теснота взаимосвязи?
54.
Цель корреляционного анализа – установить,можно ли значения одного показателя
предсказывать по значениям другого.
Задачи корреляционного анализа:
Установить, надёжны ли исходные данные при
оценке корреляции.
Установить, имеет ли она практическое значение.
55.
Если величина коэффициента корреляции по модулюбольше или ровна 0,7 , то говорят, что корреляция,
имеет практическое значение, если значение меньше
0,7 , то корреляция не имеет практического значения.
56. Корреляция
• Корелляция Пирсона (параметрический)• Ранговая корреляция
Спирмена(непараметрический)
57.
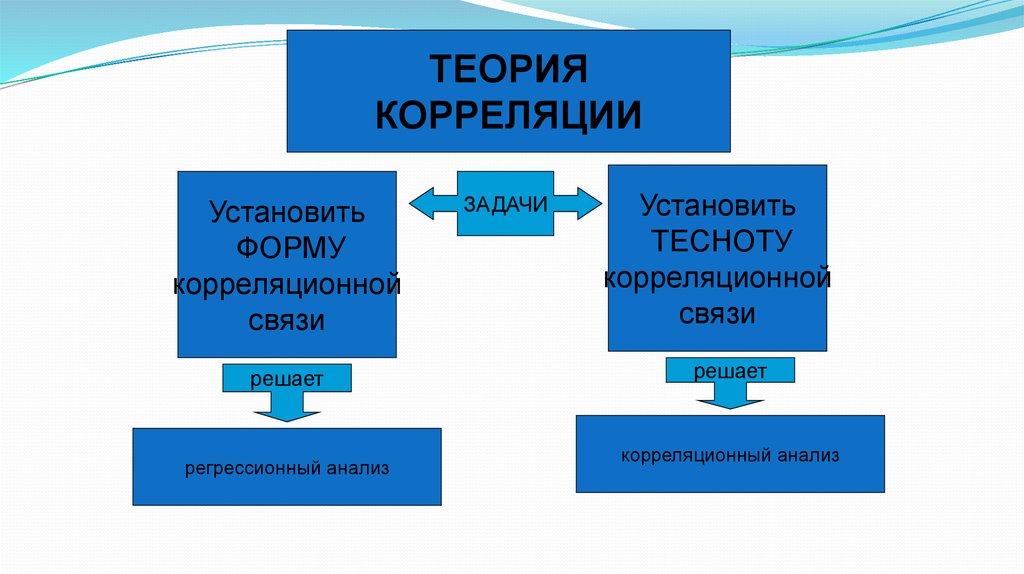
ТЕОРИЯКОРРЕЛЯЦИИ
Установить
ФОРМУ
корреляционной
связи
решает
регрессионный анализ
ЗАДАЧИ
Установить
ТЕСНОТУ
корреляционной
связи
решает
корреляционный анализ
58. Регрессионный анализ
Задачей регрессионного анализа является нахождениефункциональной зависимости между зависимой у и
независимой х переменными y = f(x), которую называют
регрессией (или функцией регрессии). График функции
называют линией или кривой регрессии.
Hа практике x задается, а y - это наблюдение какой-либо
величины на опыте, в эксперименте.
59.
В ходе регрессионного анализа определяется аналитическоевыражение связи зависимой случайной величины Y
(результативный признак) с независимыми случайными
величинами Х1, Х2, …Хm (факторами).
Практически речь идёт о том, чтобы, анализируя множество
точек на графике (т.е. множество статистических данных),
найти линию, по возможности точно отражающую
заключённую в этом множестве закономерность, тенденцию –
линию регрессии.
59
60. 1.В зависимости от числа явлений
– простой (регрессия между двумяпеременными);
– множественной (регрессия между
зависимой переменной Y и несколькими
независимыми переменными (X1, X2, …, Xn)).
61.
2.В зависимости от формы– линейной (отображается
линейной функцией, а между
изучаемыми явлениями существуют
линейные отношения);
у
х
– нелинейной (отображается
нелинейной функцией, между
изучаемыми переменными связь
носит нелинейный характер).
у
х
62. 3. По характеру связи между включенными в рассмотрение переменными
у– положительной (увеличение
значения независимой переменной
приводит к увеличению значения
зависимой переменной и наоборот);
х
у
– отрицательной (с увеличением
значения
независимой
переменной значение зависимой
переменной уменьшается).
х
63. Основные задачи
1. Определение формы зависимости.2. Отыскание подходящих значений
неизвестных параметров.
3. Оценка неизвестных значений зависимой
переменной.
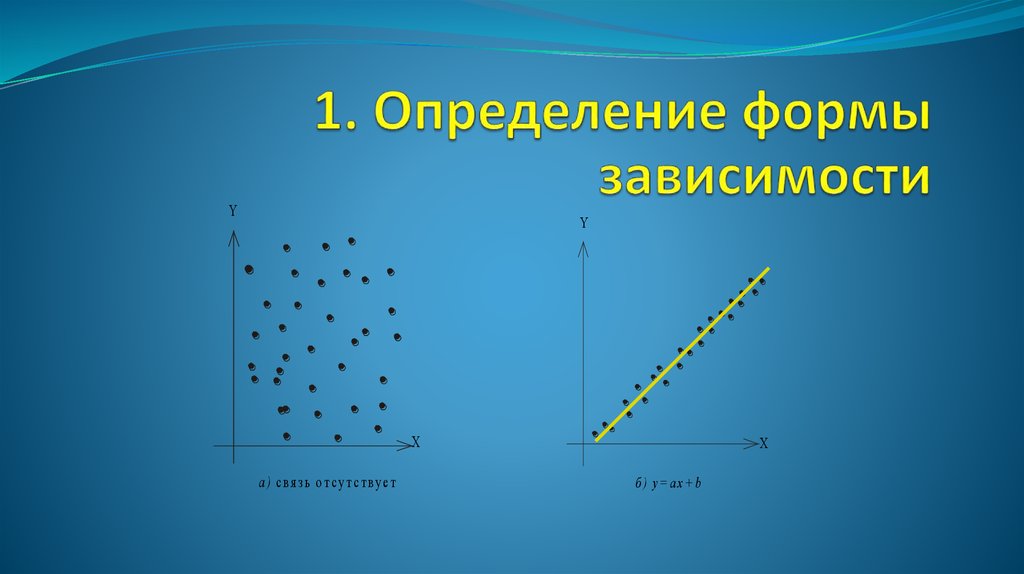
64. 1. Определение формы зависимости
YY
X
а ) с в я зь о т су т с тв у е т
X
б) y= ax+ b
65. 1. Определение формы зависимости
YY
X
X
2
в) y=ax +bx+c
г) y = asin(x b )+ c
66.
Линейную регрессию можно отразить уравнением прямой линии:Y = а · X + в, где:
Y – значения признака по линии регрессии, т. е. теоретические значения,
а – угловой коэффициент регрессии,
X – значения признака-фактора (предиктора),
в – свободный член, константа.
Если независимая переменная одна, то регрессия называется парной.
Простейшая парная регрессионная модель – линейная.
67. Нелинейная регрессия
1)Полиномиальная
2)
Гиперболическая
3)
Степенная
4) Показательная
5)
Экспоненциальная
y b0 eb1x
67
68. Определение коэффициента детерминации
R2
Для анализа общего качества уравнения линейной многофакторной
2
регрессии используют множественный коэффициент детерминации R ,
называемый также квадратом коэффициента множественной корреляции
R
и определяют долю вариации результативного признака, обусловленную
изменением факторных признаков, входящих в многофакторную
регрессионную модель.
68
69. Коэффициент детерминации
Свойства:а) 0 RI 1;
б) Чем ближе коэффициент детерминации к
1, тем лучше регрессия «объясняет»
зависимость данных;
в) В случае линейной регрессии
RI r
2
70. Порядок действий
при использовании методовкорреляционно-регрессионного анализа
1. Исследование природы
рассматриваемых переменных для
установления типа зависимости
между переменными.
71. Порядок действий
2. Сбор экспериментальных данных,обсуждение вопроса об
ограничениях:
2.1. Случайность выборки: несвязанность i-го
наблюдения с предыдущими и отсутствие
влияния на последующие.
2.2. Однородность дисперсий: рассеяния должны
быть
одинаковыми
для
всех
значений
независимого переменного.
2.3. Нормальность распределений.
72. Порядок действий
3. Построение диаграммы разброса.4. Измерение тесноты связи, вычисление
выборочного коэффициента корреляции.
5. Установление общего вида зависимости
(линейная, параболическая и т.д.)
73. Порядок действий
6. Построение эмпирической линиирегрессии методом наименьших
квадратов.
7. Исследование статистических свойств
регрессионной зависимости, оценка
адекватности модели.





































































 mathematics
mathematics








