Геометрия_2часть_ЕГЭ(1)

1.

2.

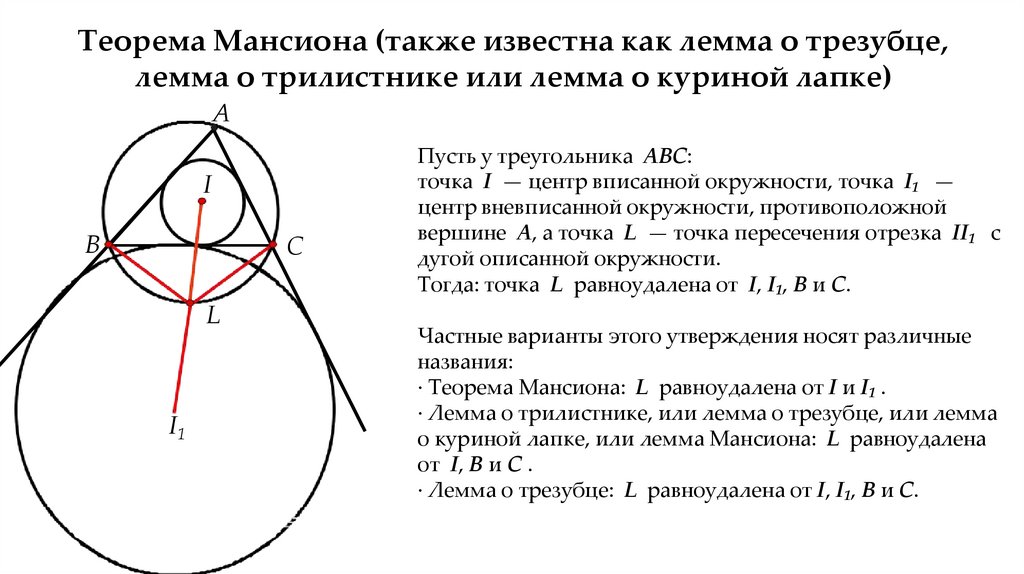
Теорема Мансиона (также известна как лемма о трезубце,
лемма о трилистнике или лемма о куриной лапке)
А
I
B
C
L
I1
Пусть у треугольника ABC:
точка I — центр вписанной окружности, точка I1 —
центр вневписанной окружности, противоположной
вершине A, а точка L — точка пересечения отрезка II1 с
дугой описанной окружности.
Тогда: точка L равноудалена от I, I1, B и C.
Частные варианты этого утверждения носят различные
названия:
· Теорема Мансиона: L равноудалена от I и I1 .
· Лемма о трилистнике, или лемма о трезубце, или лемма
о куриной лапке, или лемма Мансиона: L равноудалена
от I, B и C .
· Лемма о трезубце: L равноудалена от I, I1, B и C.

3.

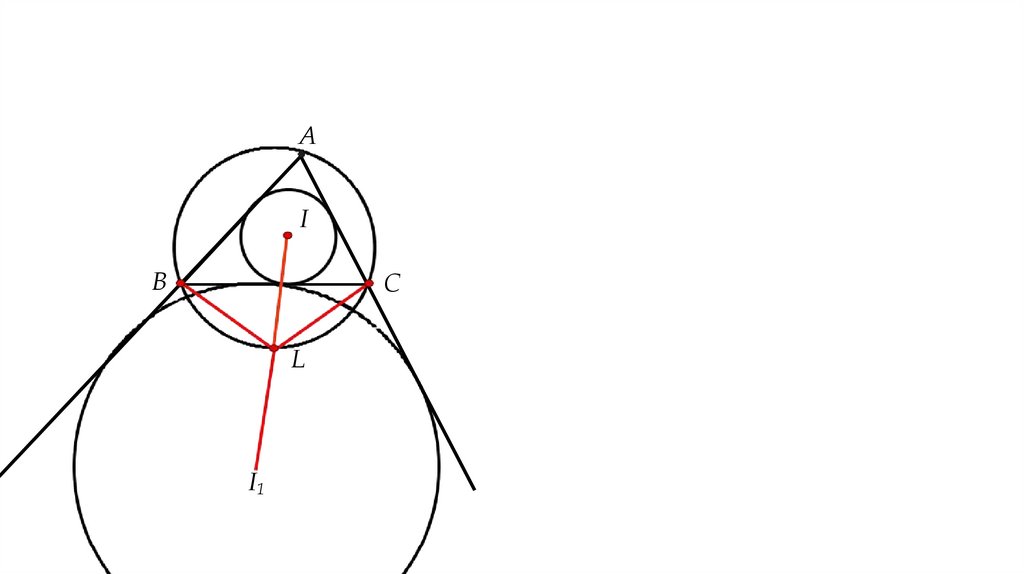
А
I
B
C
L
I1

4.

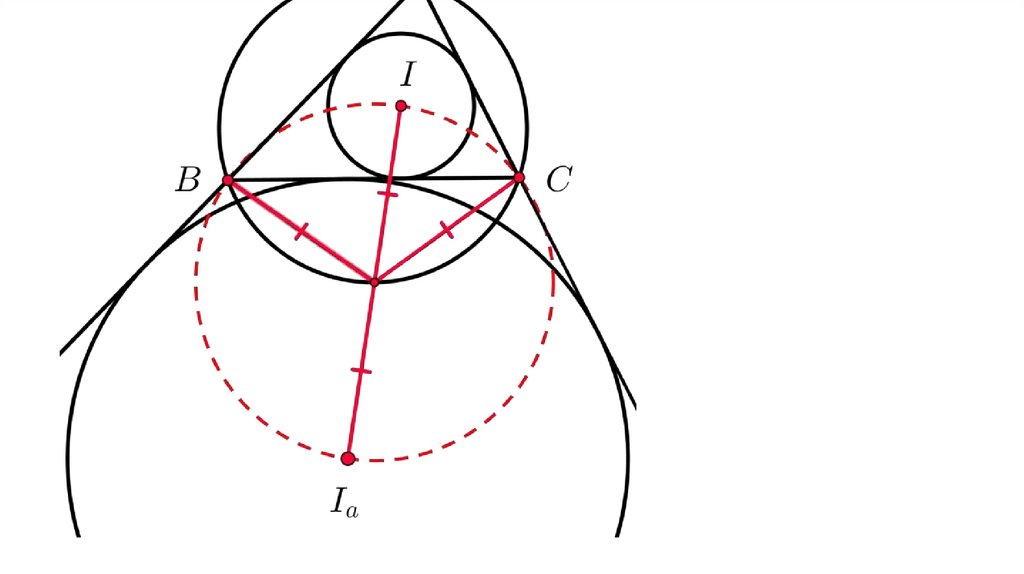
А
I
B
C
L
I1

5.

Пусть у треугольника ABC точка I — центр вписанной окружности, точка I1 — центр
вневписанной окружности, противоположной вершине A , а точка L — точка пересечения
отрезка II1 с дугой описанной окружности. Тогда точка L равноудалена от I, I1, B и C.
Частные варианты этого утверждения носят различные названия
· Теорема Мансиона: L равноудалена от I и I1 .
· Лемма о трилистнике, или лемма о трезубце, или лемма Мансиона: L равноудалена
от I, B и C .
· Лемма о трезубце: L равноудалена от I, I1, B и C.
Другой вариант задания точки L — как центра дуги BC описанной окружности, не
содержащей точки A^[4] .

6.

7.

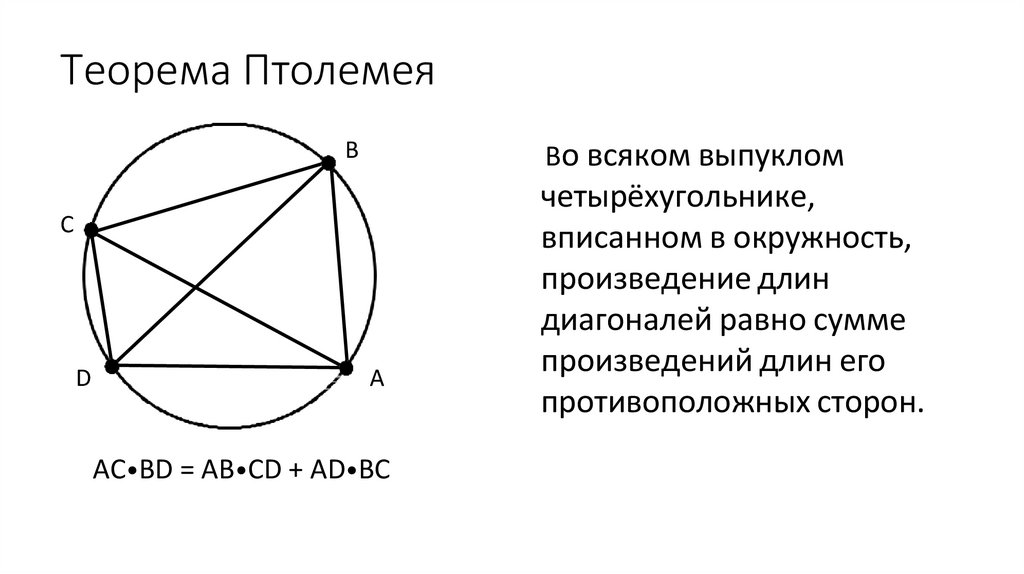
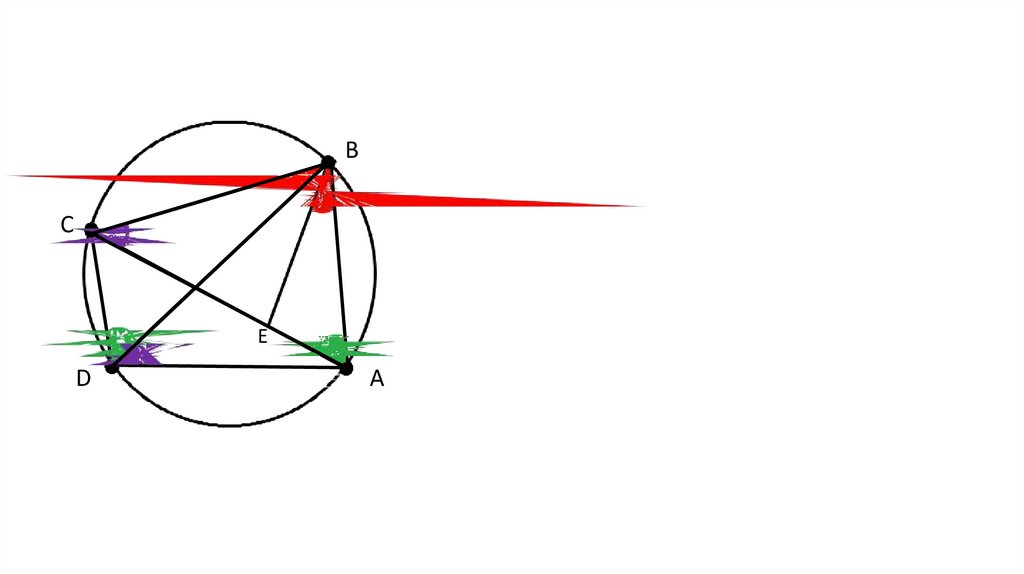
Теорема Птолемея
B
Во всяком выпуклом
C
D
A
AC•BD = AB•CD + AD•BC
четырёхугольнике,
вписанном в окружность,
произведение длин
диагоналей равно сумме
произведений длин его
противоположных сторон.

8.

B
C
E
D
A