Вписанные и описанные окружности

1.

ВПИСАННЫЕ И
ОПИСАННЫЕ
ОКРУЖНОСТИ
Выполнил: ученик 9 «А» класса
Чуднов Иван

2.

Цели и задачи :
■ Основной задачей и главной целью моей работы является
изучение темы «Вписанные и описанные окружности». А
точнее:
– Расширение своих знаний по теме «окружности»
– Систематизация их для упрощения процесса решение задач

3.

В истории:
Гиппократ Хиосский
Евклид
(5 в. до н. э.)
(родился в 330 году до н. э.)

4.

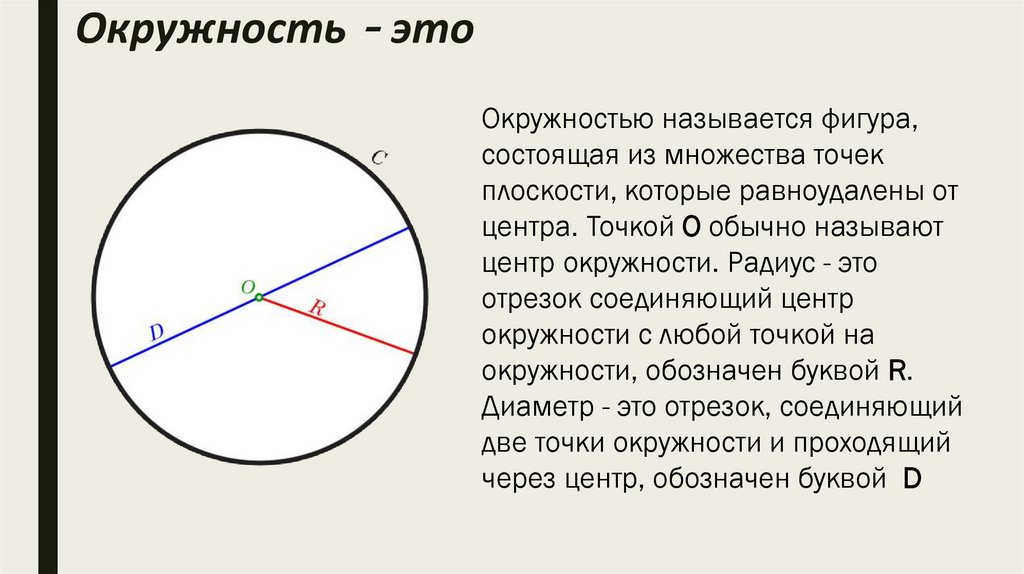
Окружность - это
Окружностью называется фигура,
состоящая из множества точек
плоскости, которые равноудалены от
центра. Точкой О обычно называют
центр окружности. Радиус - это
отрезок соединяющий центр
окружности с любой точкой на
окружности, обозначен буквой R.
Диаметр - это отрезок, соединяющий
две точки окружности и проходящий
через центр, обозначен буквой D

5.

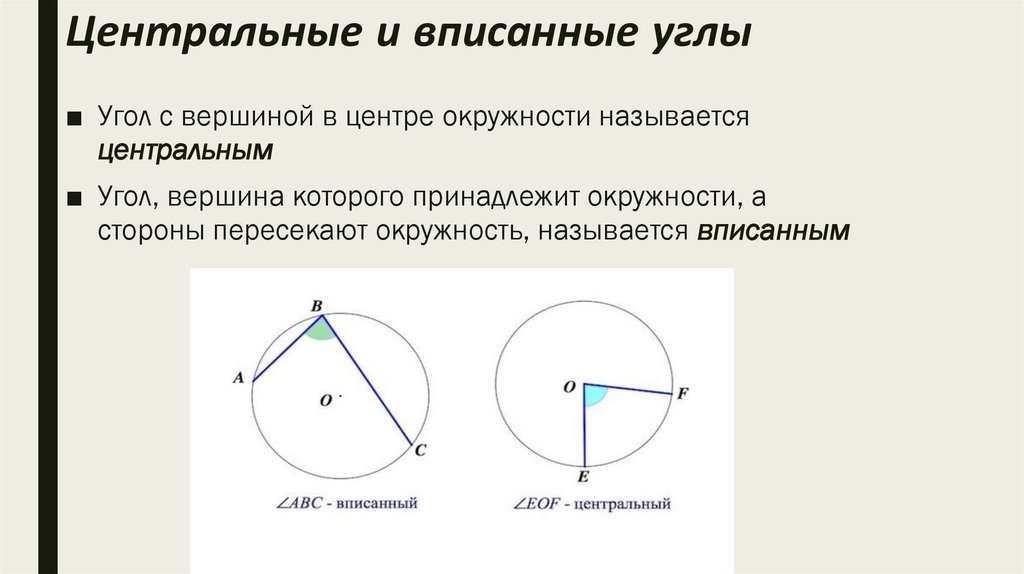
Центральные и вписанные углы
■ Угол с вершиной в центре окружности называется
центральным
■ Угол, вершина которого принадлежит окружности, а
стороны пересекают окружность, называется вписанным

6.

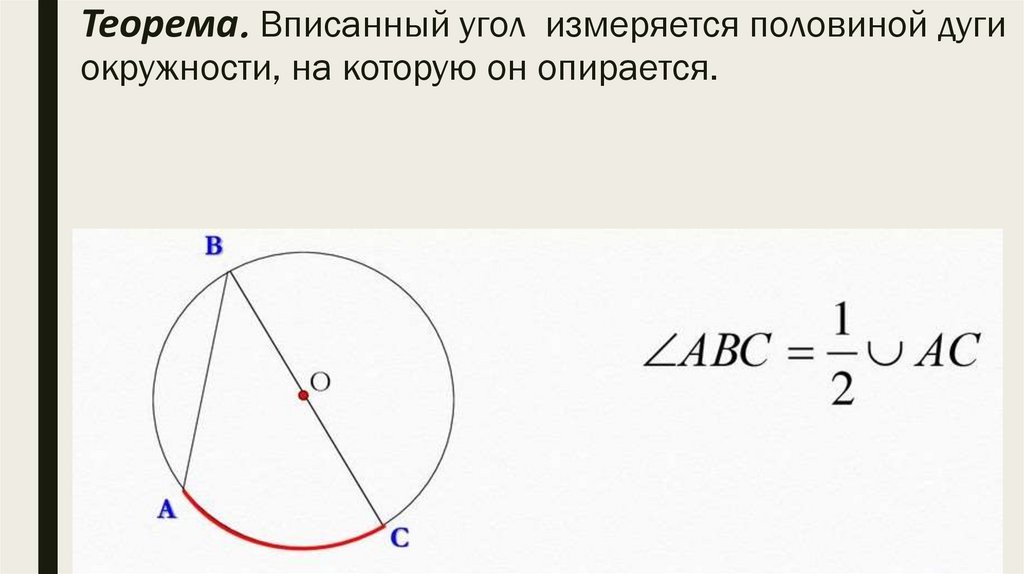
Теорема. Вписанный угол измеряется половиной дуги
окружности, на которую он опирается.

7.

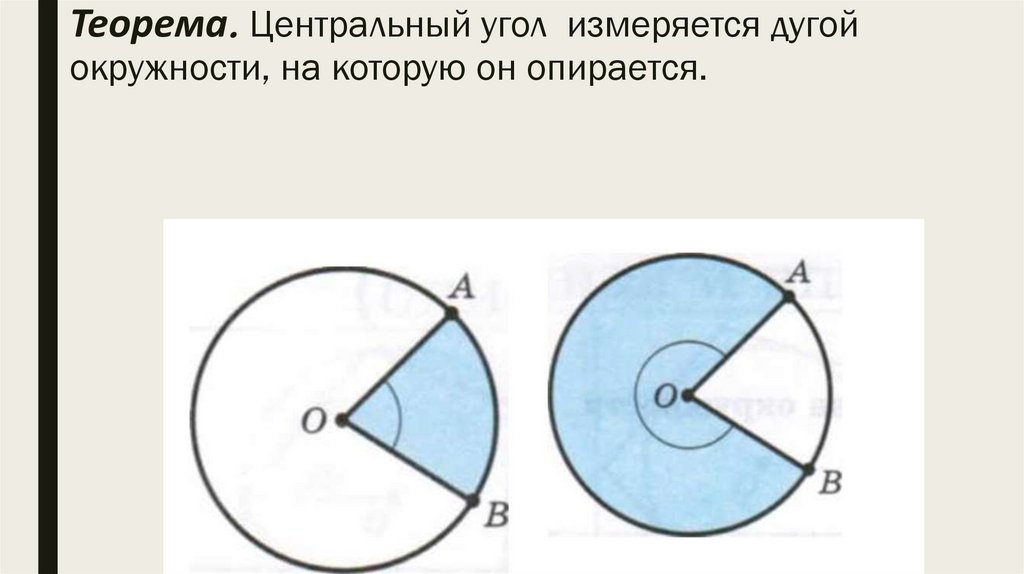
Теорема. Центральный угол измеряется дугой
окружности, на которую он опирается.

8.

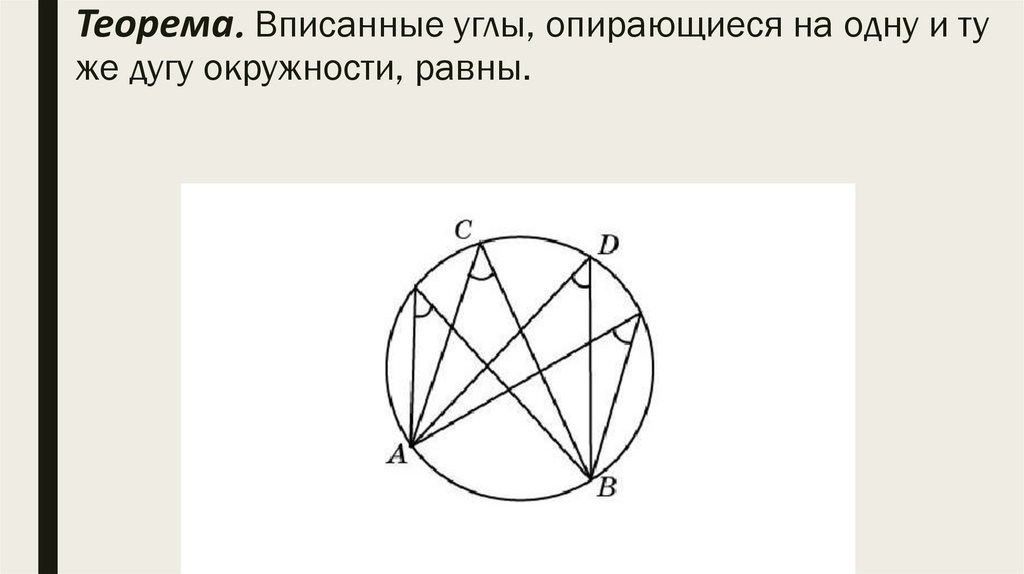
Теорема. Вписанные углы, опирающиеся на одну и ту
же дугу окружности, равны.

9.

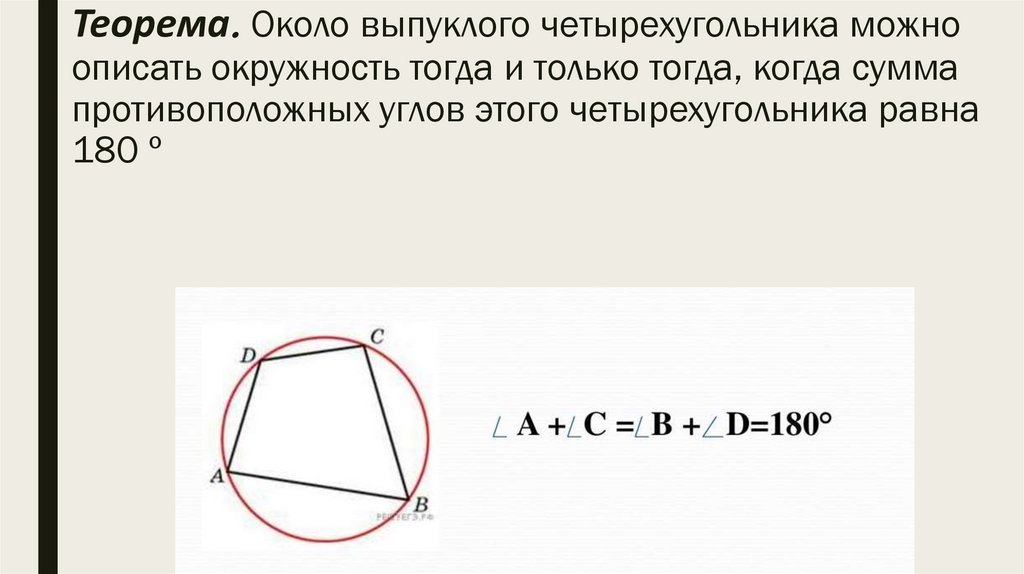
Теорема. Около выпуклого четырехугольника можно
описать окружность тогда и только тогда, когда сумма
противоположных углов этого четырехугольника равна
180 º

10.

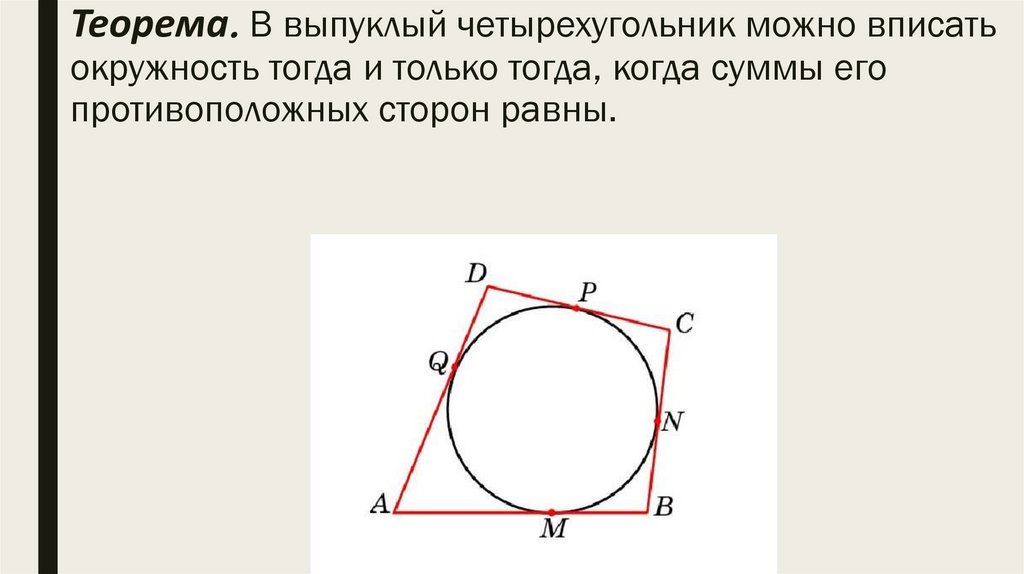
Теорема. В выпуклый четырехугольник можно вписать
окружность тогда и только тогда, когда суммы его
противоположных сторон равны.

11.

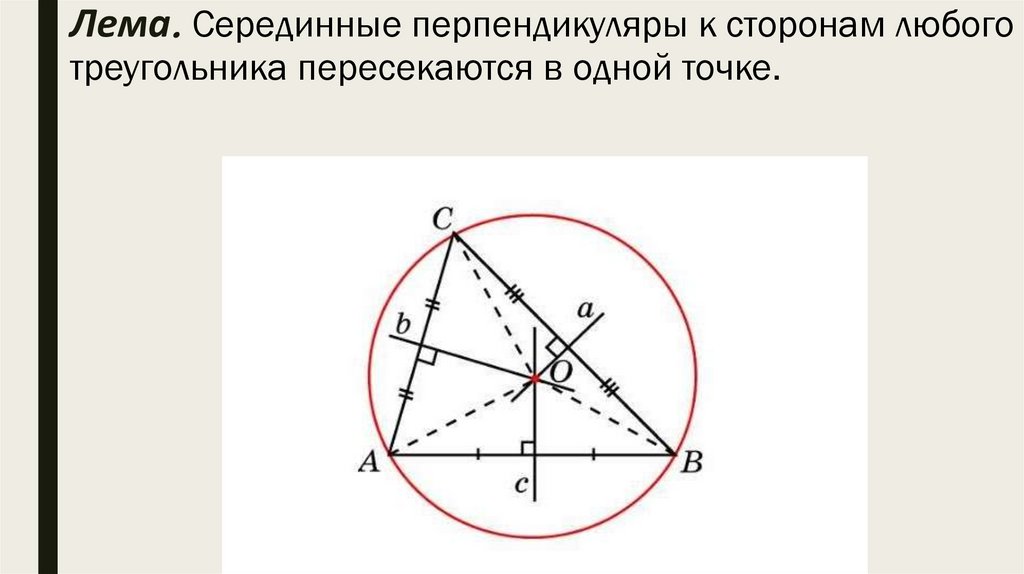
Лема. Серединные перпендикуляры к сторонам любого
треугольника пересекаются в одной точке.

12.

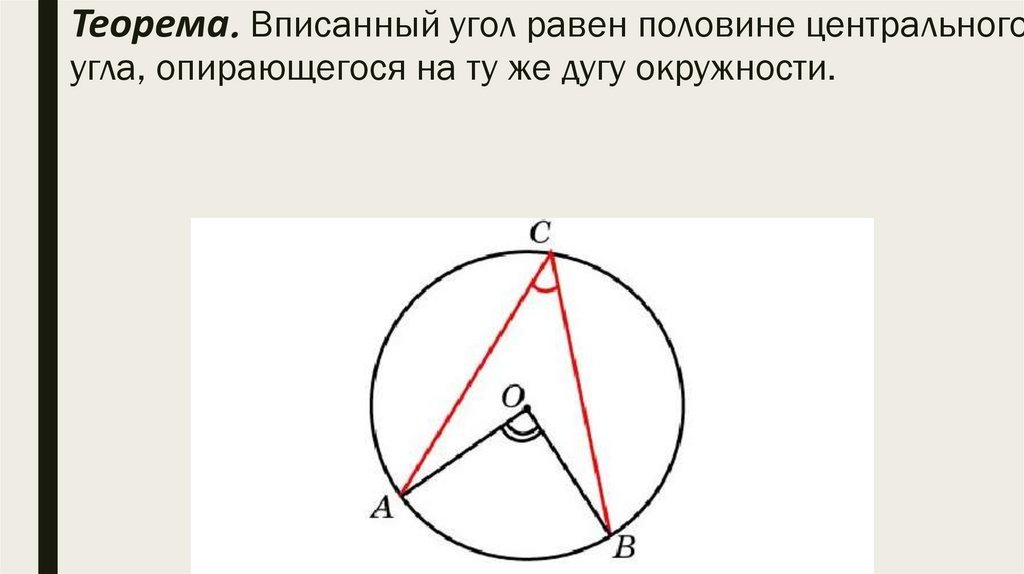
Теорема. Вписанный угол равен половине центрального
угла, опирающегося на ту же дугу окружности.

13.

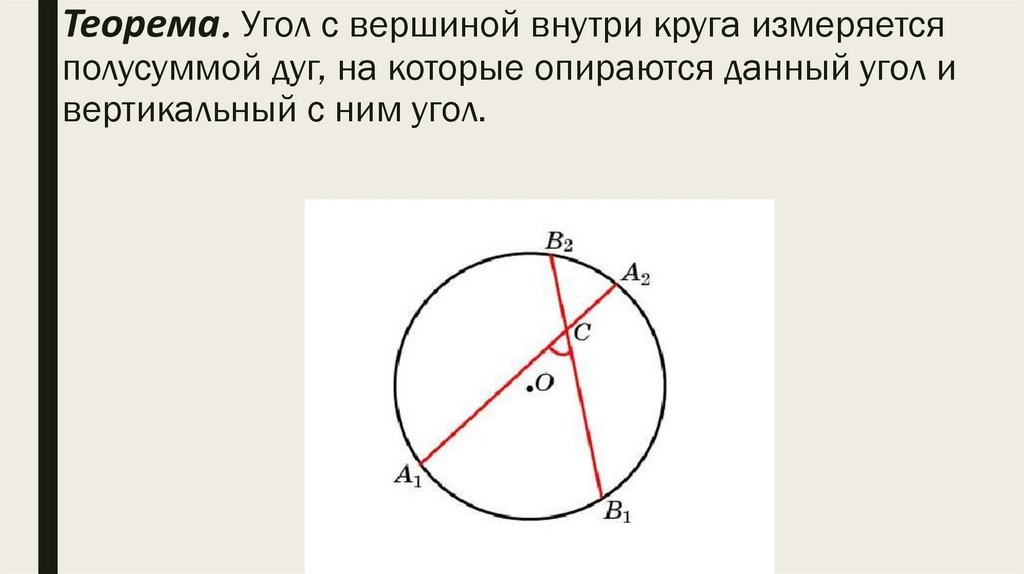
Теорема. Угол с вершиной внутри круга измеряется
полусуммой дуг, на которые опираются данный угол и
вертикальный с ним угол.

14.

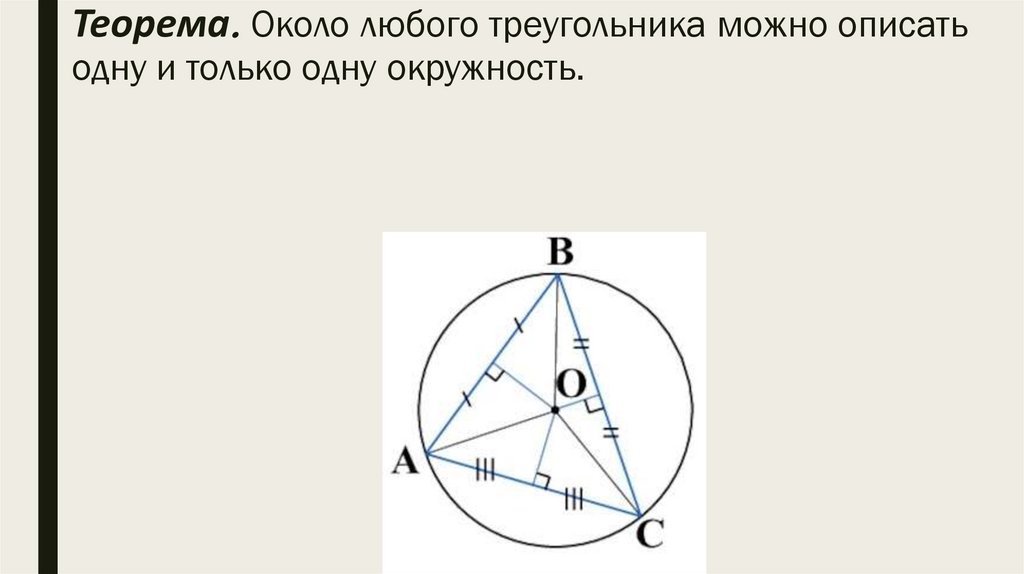
Теорема. Около любого треугольника можно описать
одну и только одну окружность.

15.

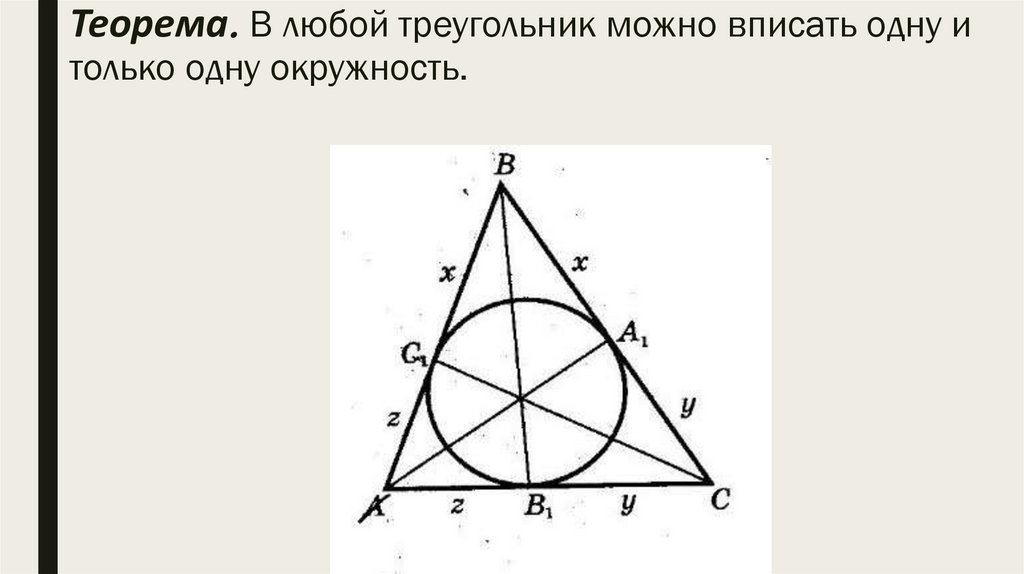
Теорема. В любой треугольник можно вписать одну и
только одну окружность.

16.

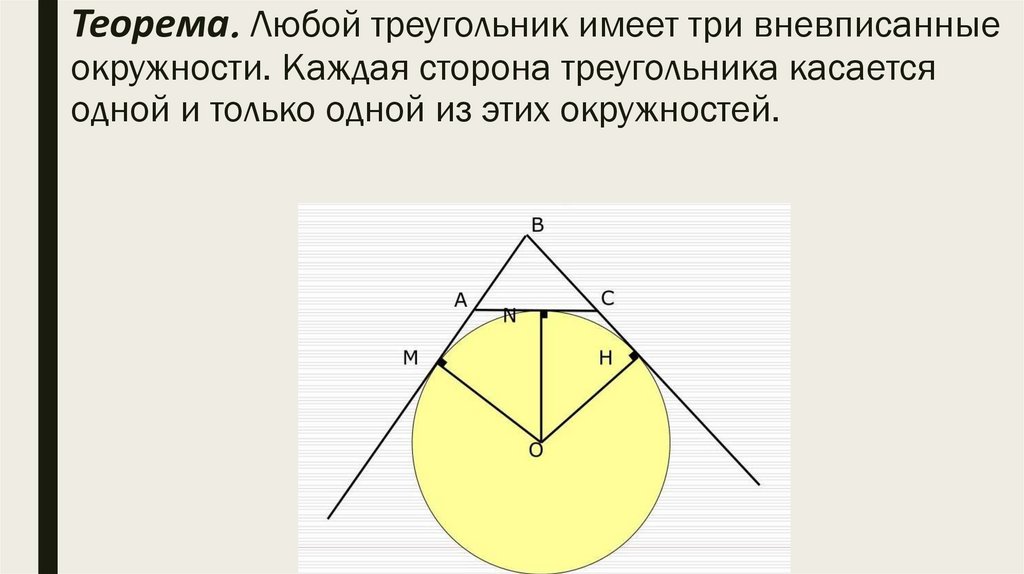
Теорема. Любой треугольник имеет три вневписанные
окружности. Каждая сторона треугольника касается
одной и только одной из этих окружностей.

17.

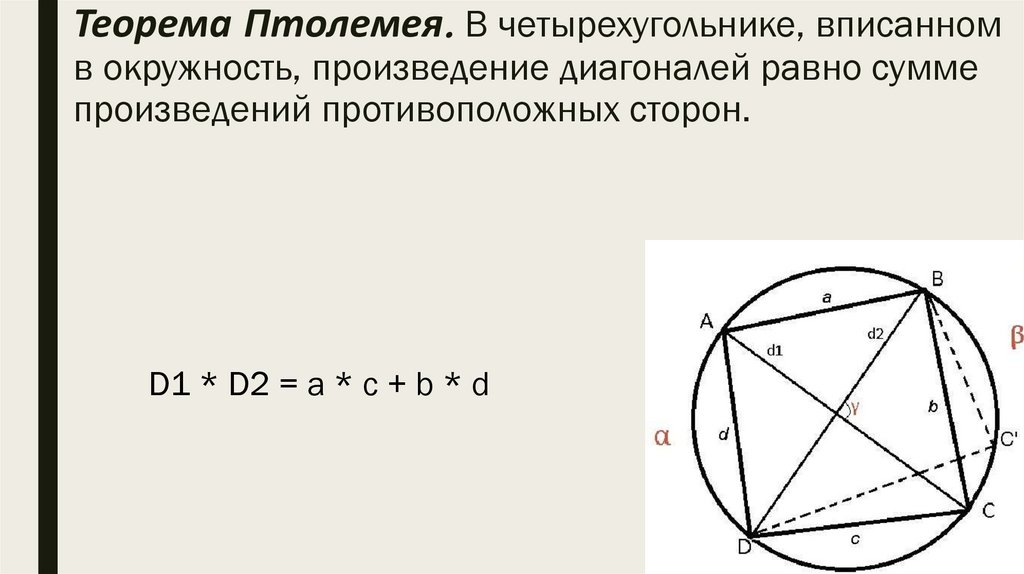
Теорема Птолемея. В четырехугольнике, вписанном
в окружность, произведение диагоналей равно сумме
произведений противоположных сторон.
D1 * D2 = a * c + b * d

18.

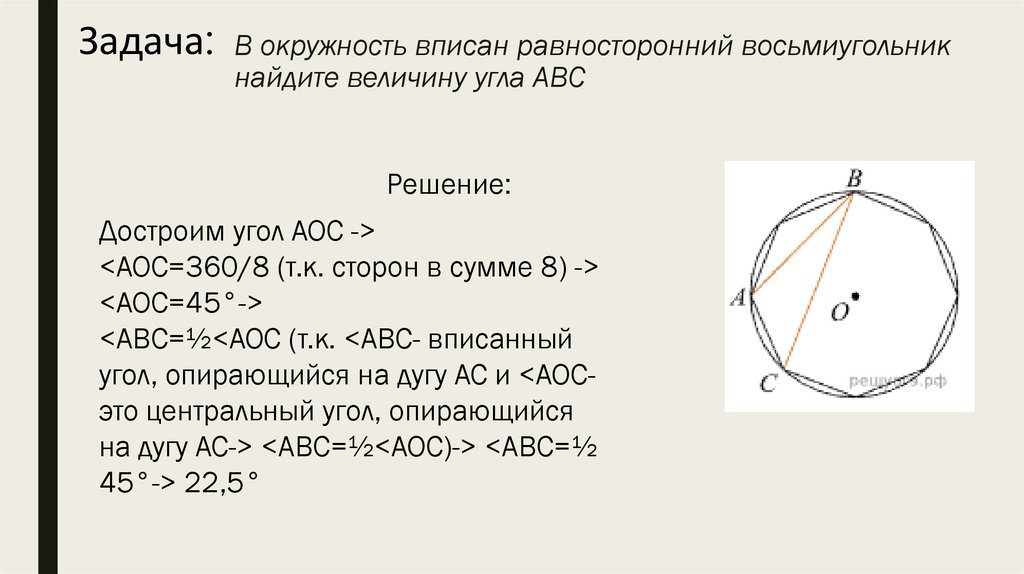
Задача: В окружность вписан равносторонний восьмиугольник
найдите величину угла ABC
Решение:
Достроим угол AOC ->
<AOC=360/8 (т.к. сторон в сумме 8) ->
<AOC=45°->
<ABC=½<AOC (т.к. <ABC- вписанный
угол, опирающийся на дугу AC и <AOCэто центральный угол, опирающийся
на дугу AC-> <ABC=½<AOC)-> <ABC=½
45°-> 22,5°

19.

Заключение:
■ В процессе выполнения проекта я углубил свои знания на
теме «Вписанные и описанные окружности», освоил
множество теорем, систематизировал знания по данной
теме и закрепил методы решения этих задач на практике

20.

Спасибо за внимание