Similar presentations:
Вписанные и описанные многоугольники
1. Вписанные и описанные многоугольники
Урок 52.
Вписанные углыABK ACK ADK
Вписанные углы, которые
опираются на одну и ту же
дугу, равны между собой.
Вписанный угол, который
опирается на диаметр, равен 90о.
ABD ACD 90
o
3. Вписанные углы
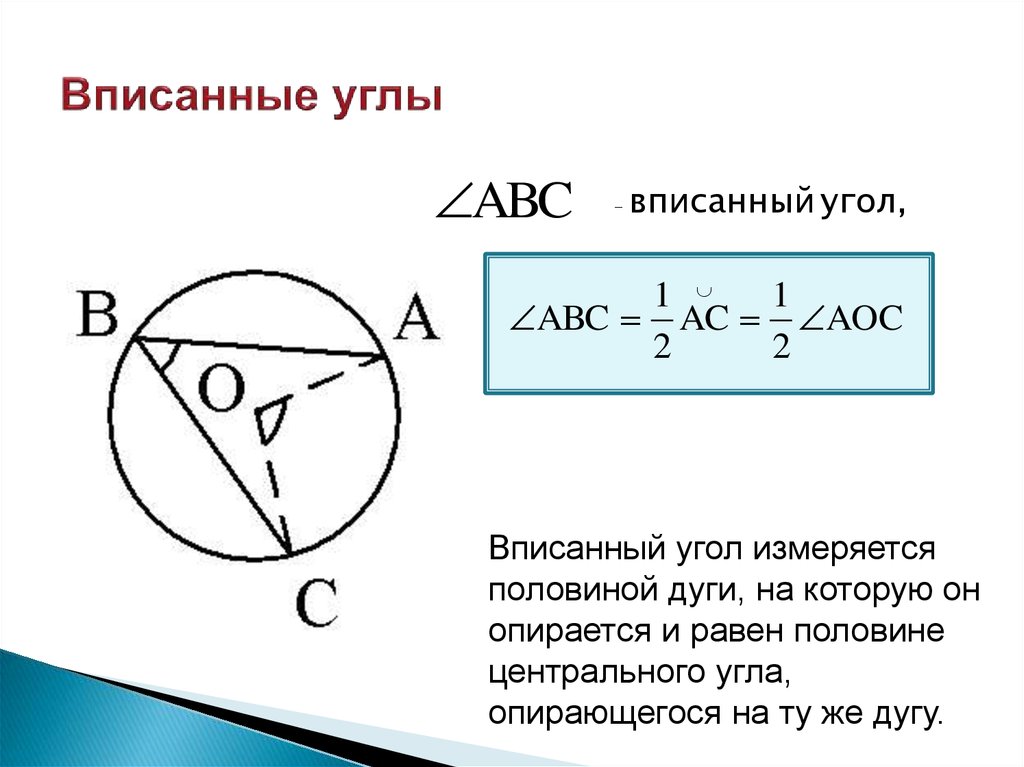
ABC-
вписанный угол,
1
1
ABC AC AOC
2
2
Вписанный угол измеряется
половиной дуги, на которую он
опирается и равен половине
центрального угла,
опирающегося на ту же дугу.
4.
Описаннаяокружность
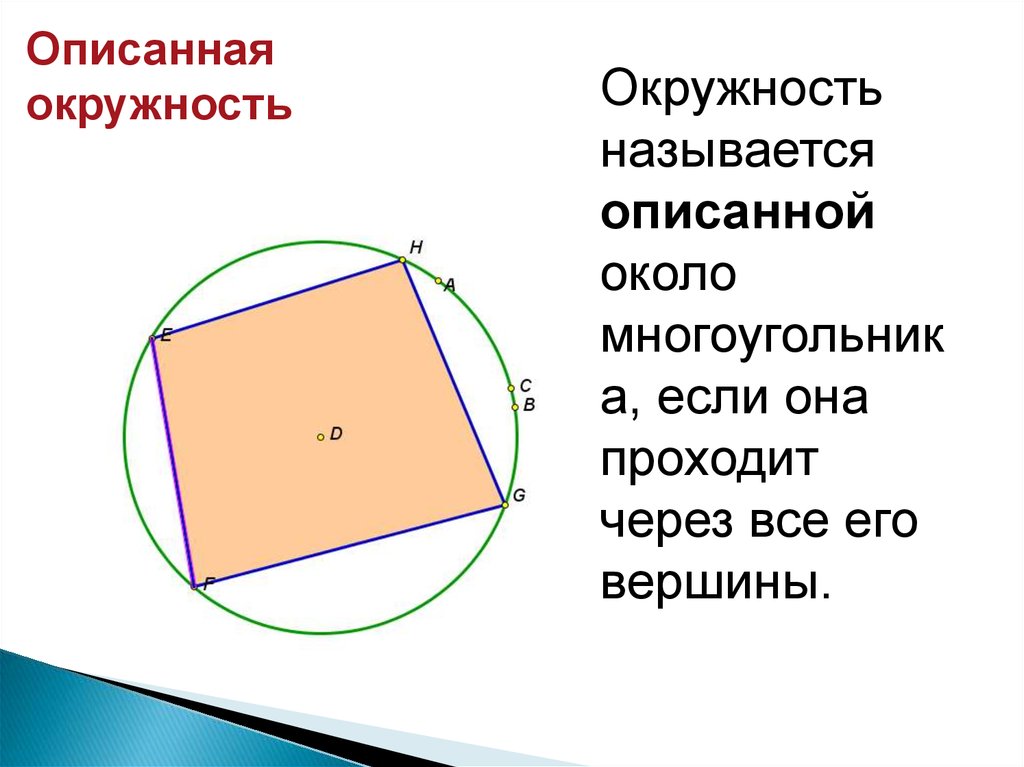
Окружность
называется
описанной
около
многоугольник
а, если она
проходит
через все его
вершины.
5.
Описаннаяокружность
Расположение центра описанной окружности в
зависимости от вида треугольника:
Остроугольный треугольник
Тупоугольный треугольник
о
о
о
Прямоугольный
треугольник
6.
Описаннаяокружность
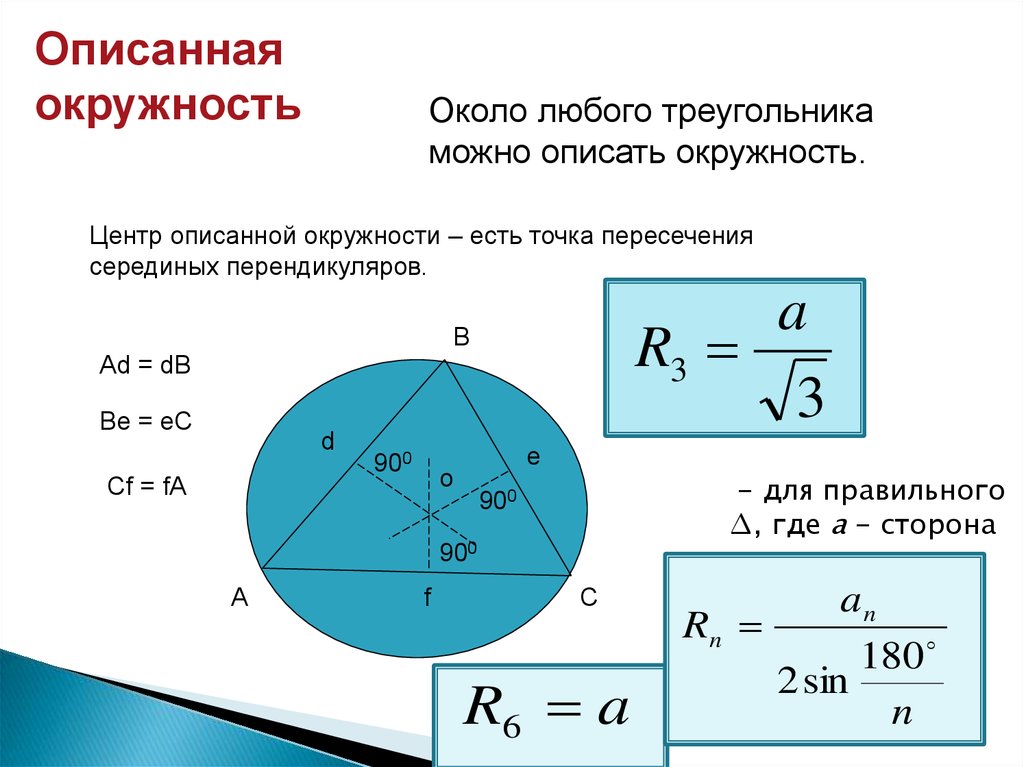
Около любого треугольника
можно описать окружность.
Центр описанной окружности – есть точка пересечения
серединых перендикуляров.
a
R3
3
В
Ad = dB
Be = eC
d
Cf = fA
900
e
o
- для правильного
∆, где а - сторона
900
900
А
f
С
R6 a
an
Rn
180
2 sin
n
7.
Описаннаяокружность
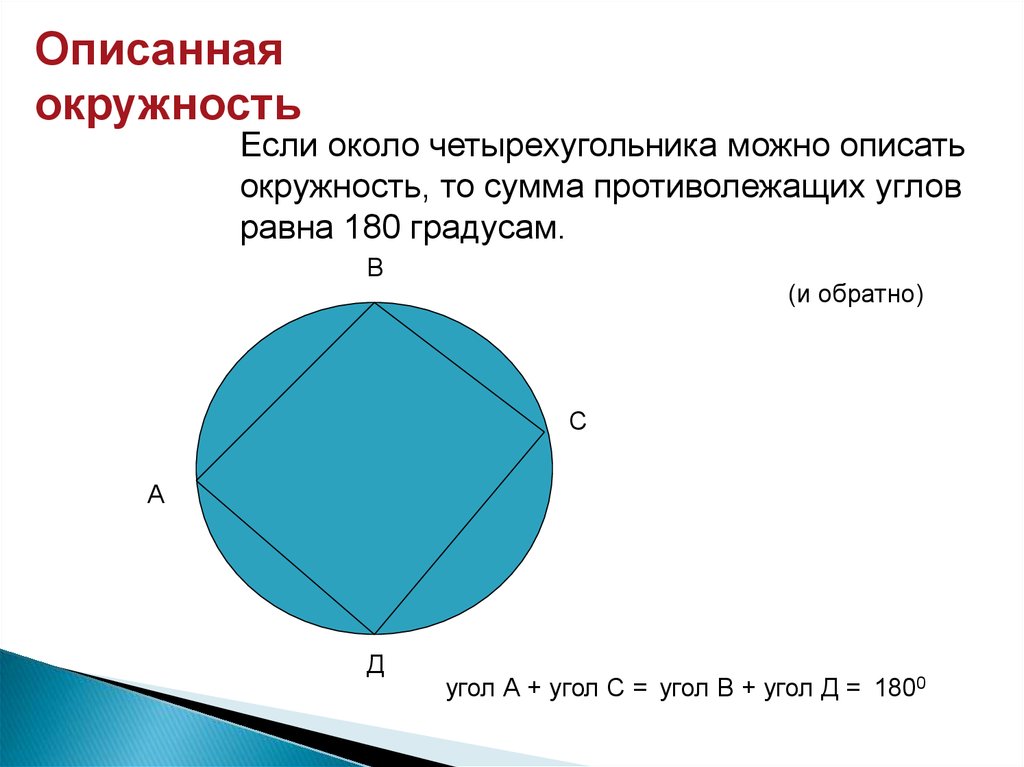
Если около четырехугольника можно описать
окружность, то сумма противолежащих углов
равна 180 градусам.
В
(и обратно)
С
А
Д
угол А + угол С = угол В + угол Д = 1800
8.
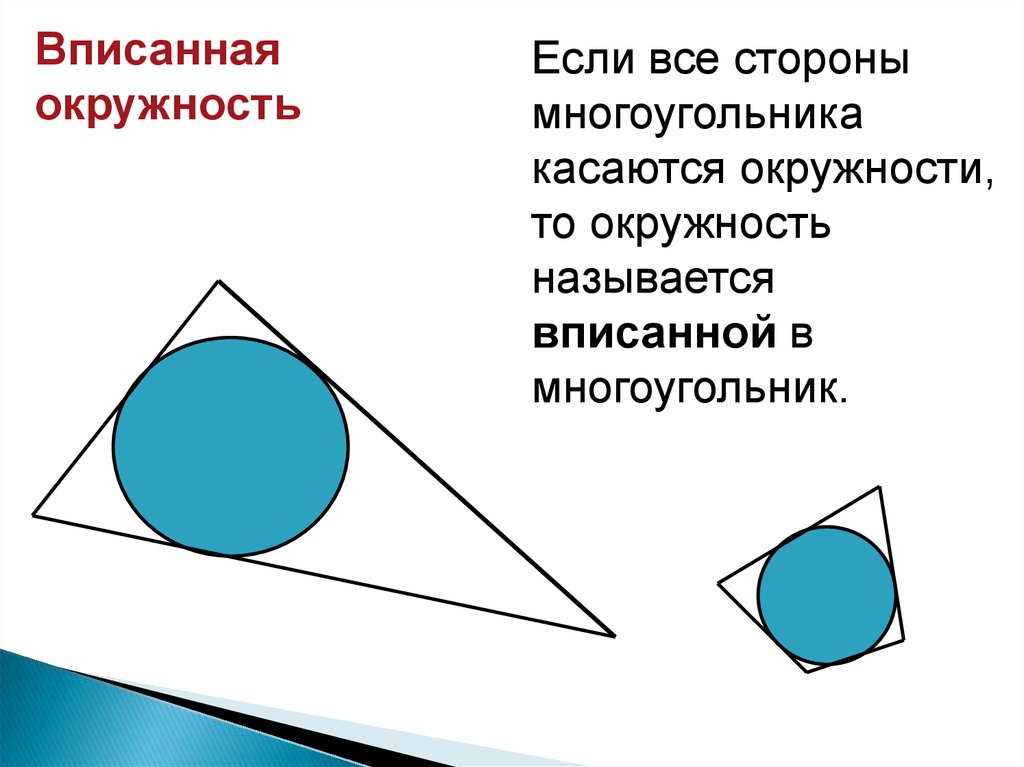
Вписаннаяокружность
Если все стороны
многоугольника
касаются окружности,
то окружность
называется
вписанной в
многоугольник.
9.
Вписаннаяокружность
В любой треугольник можно вписать окружность.
Центр вписанной окружности – есть
точка пересечения
биссектрис его углов.
B
M
N
r3
a
2 3
o
A
- для правильного ∆,
где a - сторона
an
rn
180
2 tg
n
P
a 3
r6
2
C
10.
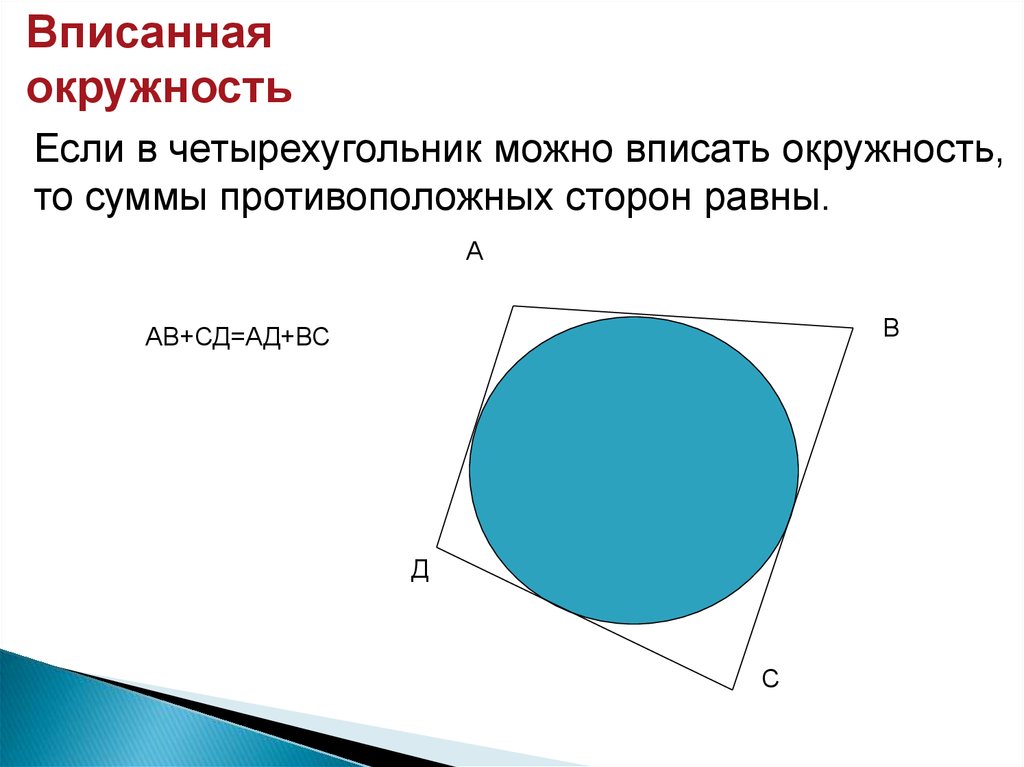
Вписаннаяокружность
Если в четырехугольник можно вписать окружность,
то суммы противоположных сторон равны.
А
В
АВ+СД=АД+ВС
Д
С
11.
Формулы площадей треугольников.=p*r
S
S
=
где
A*B*C
4*R
Р – полупериметр треугольника
r – радиус вписанной окружности
где
A, B, C - стороны треугольника
R- радиус описанной окружности
12.
Задача 1.Найдите радиус R окружности, описанной около
треугольника ABC, если стороны квадратных клеток
равны 1. В ответе укажите
Подсказка:
Т.к. окружность описана
около прямоугольного
треугольника, то его
гипотенуза является
диаметром окружности.
13.
Задача 2.Найдите радиус окружности, описанной около
правильного треугольника ABC, считая стороны
квадратных клеток равными 1.
Подсказка:
Центр окружности,
описанной около
треугольник – точка
пересечения серединных
перпендикуляров.
Подсказка 2:
Медианы, биссектрисы,
высоты в треугольнике
точкой пересечения делятся
в отношении 2:1, считая от
вершины треугольника.
14.
Задача 3.Найдите радиус окружности, вписанной в
треугольник ABC, считая стороны квадратных
клеток равными 1.
Подсказка:
S
=p*r
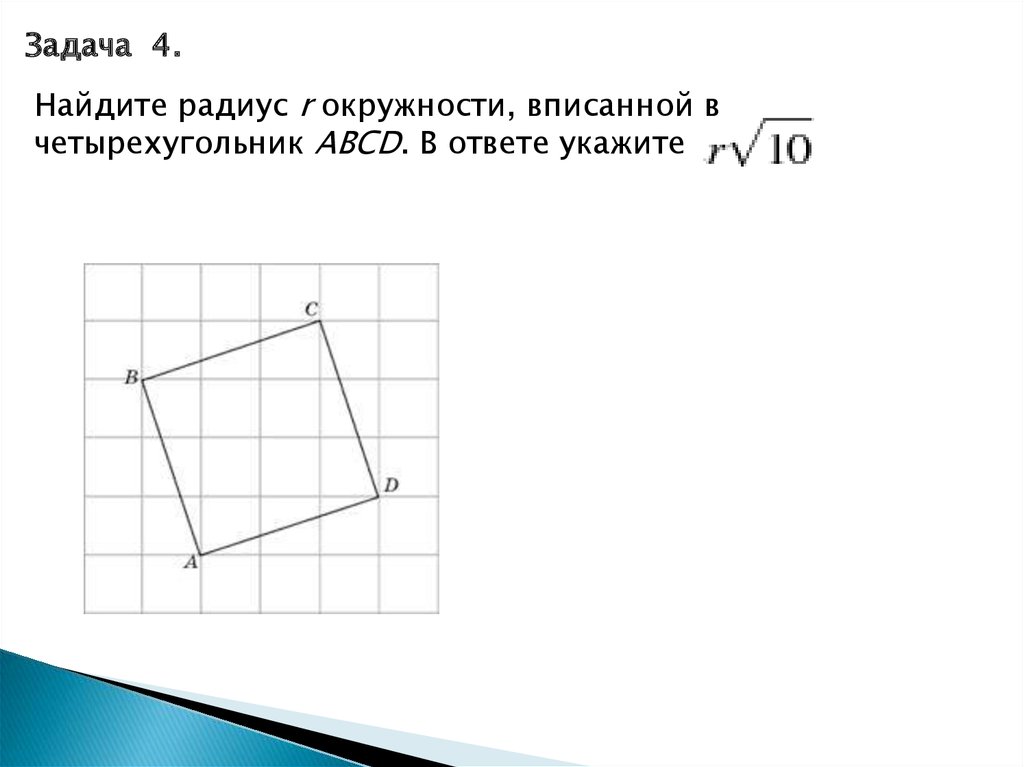
15.
Задача 4.Найдите радиус r окружности, вписанной в
четырехугольник ABCD. В ответе укажите
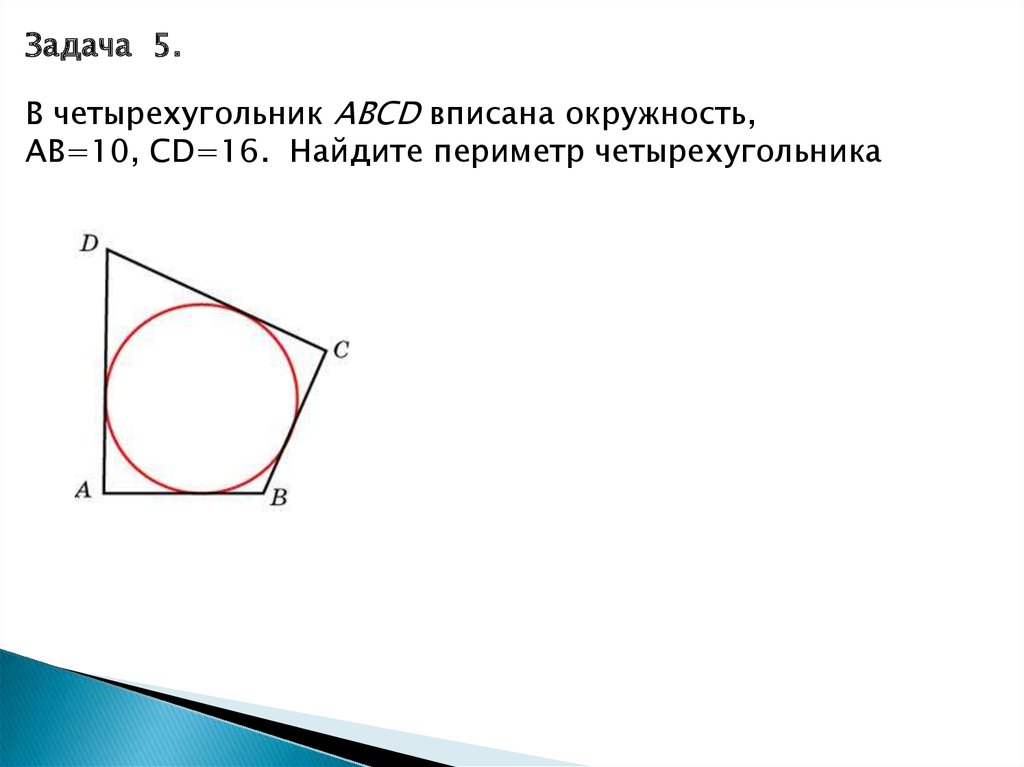
16.
Задача 5.В четырехугольник ABCD вписана окружность,
AB=10, CD=16. Найдите периметр четырехугольника








 mathematics
mathematics








