признак перпендикурярности прямой и плоскости

1. Признак перпендикулярности прямой и плоскости

10 класс

2. Перпендикулярность в пространстве

Обелиск
Башня

3. Цель: знать признак перпендикулярности прямой и плоскости

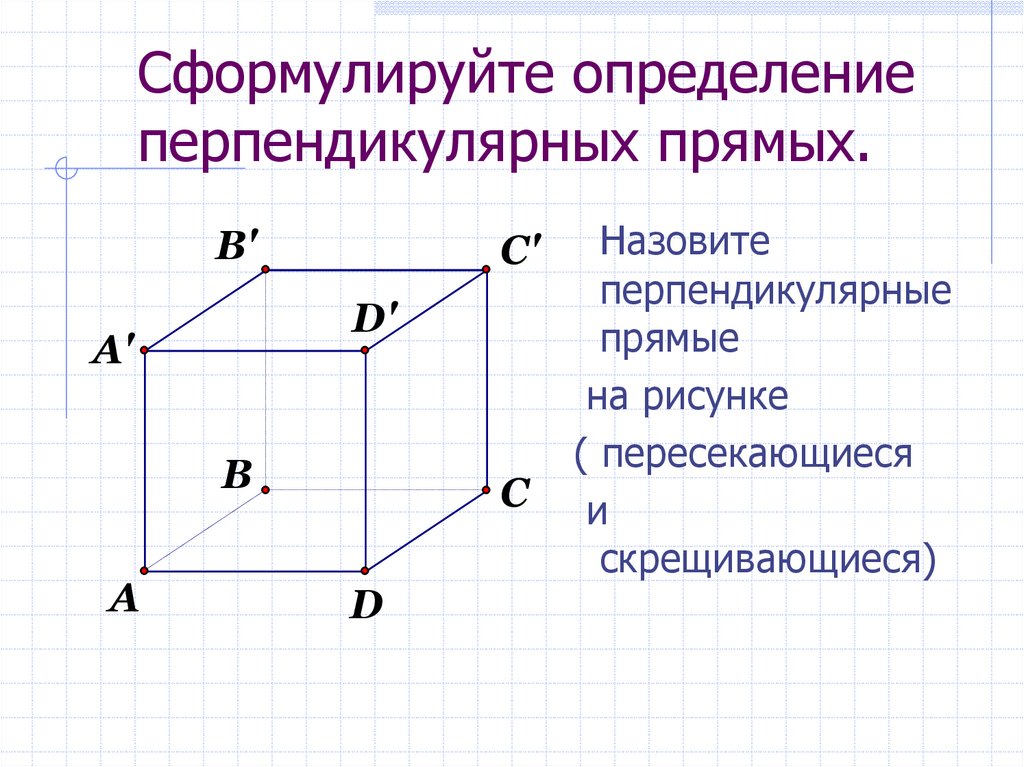
4. Сформулируйте определение перпендикулярных прямых.

B'
C'
D'
A'
B
A
C
D
Назовите
перпендикулярные
прямые
на рисунке
( пересекающиеся
и
скрещивающиеся)

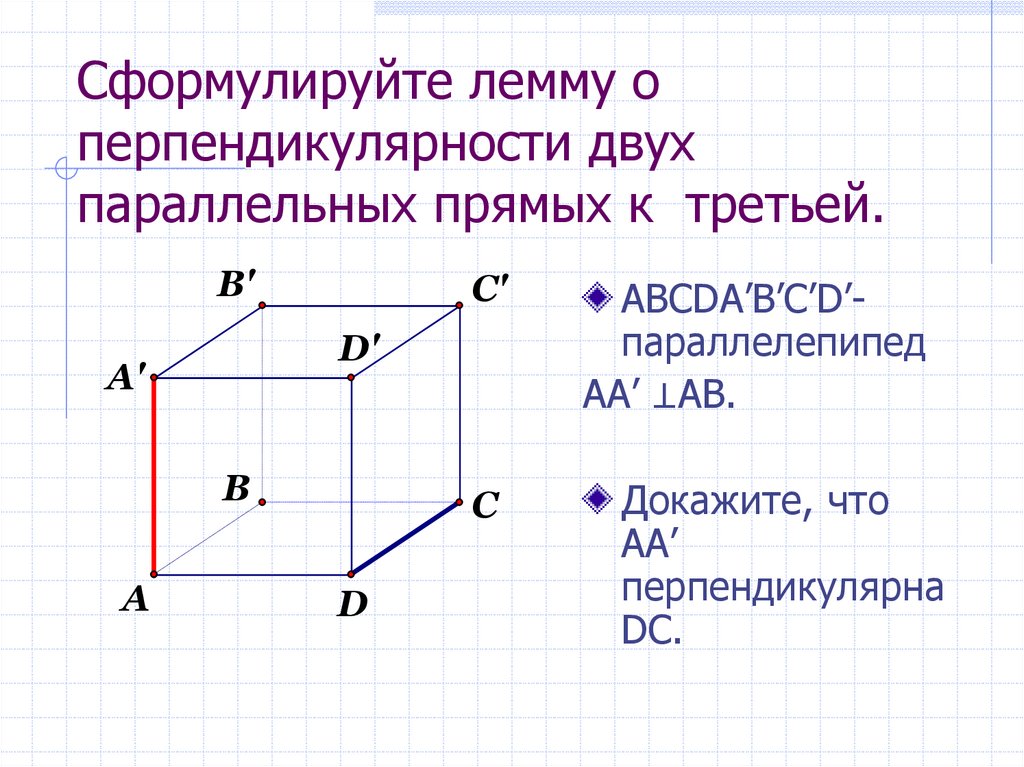
5. Сформулируйте лемму о перпендикулярности двух параллельных прямых к третьей.

B'
ABCDA’B’C’D’параллелепипед
AA’ ⊥AB.
C
Докажите, что
АА’
перпендикулярна
DС.
D'
A'
B
A
C'
D

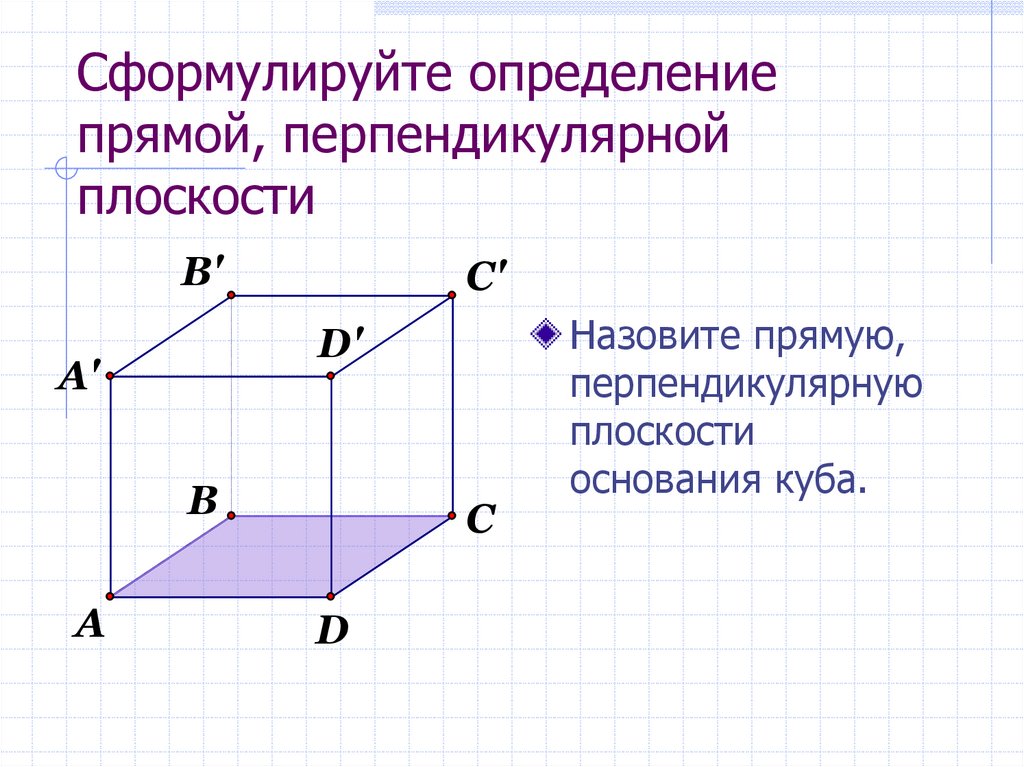
6. Cформулируйте определение прямой, перпендикулярной плоскости

B'
C'
D'
A'
B
A
C
D
Назовите прямую,
перпендикулярную
плоскости
основания куба.

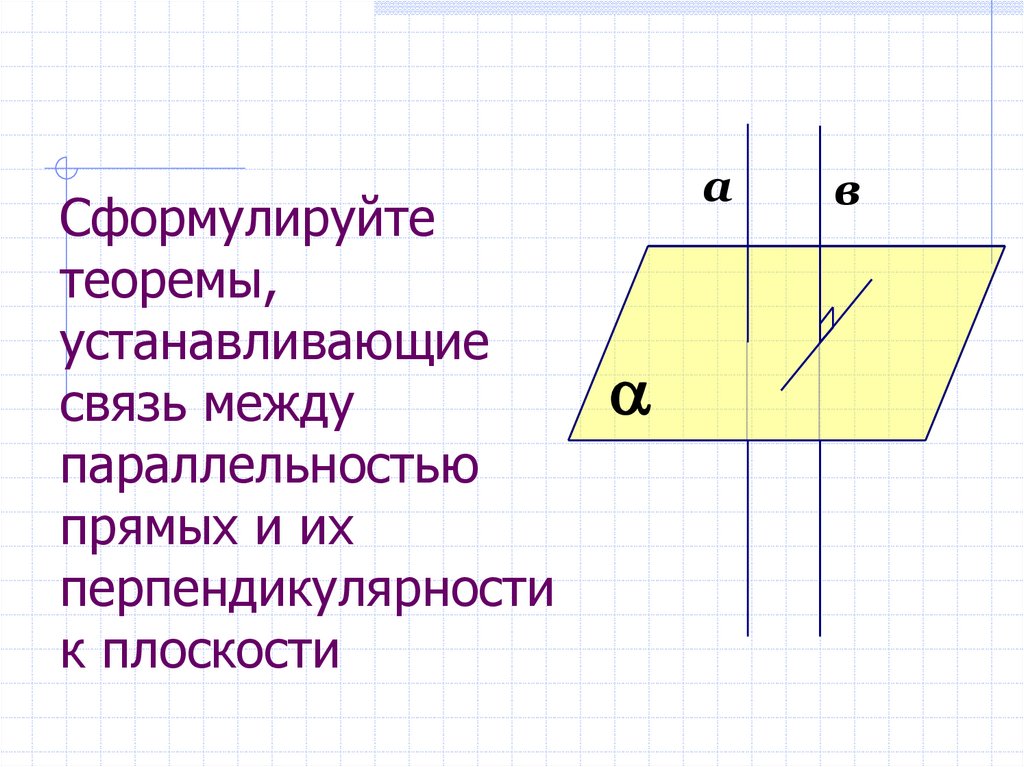
7. Сформулируйте теоремы, устанавливающие связь между параллельностью прямых и их перпендикулярности к плоскости

а
в

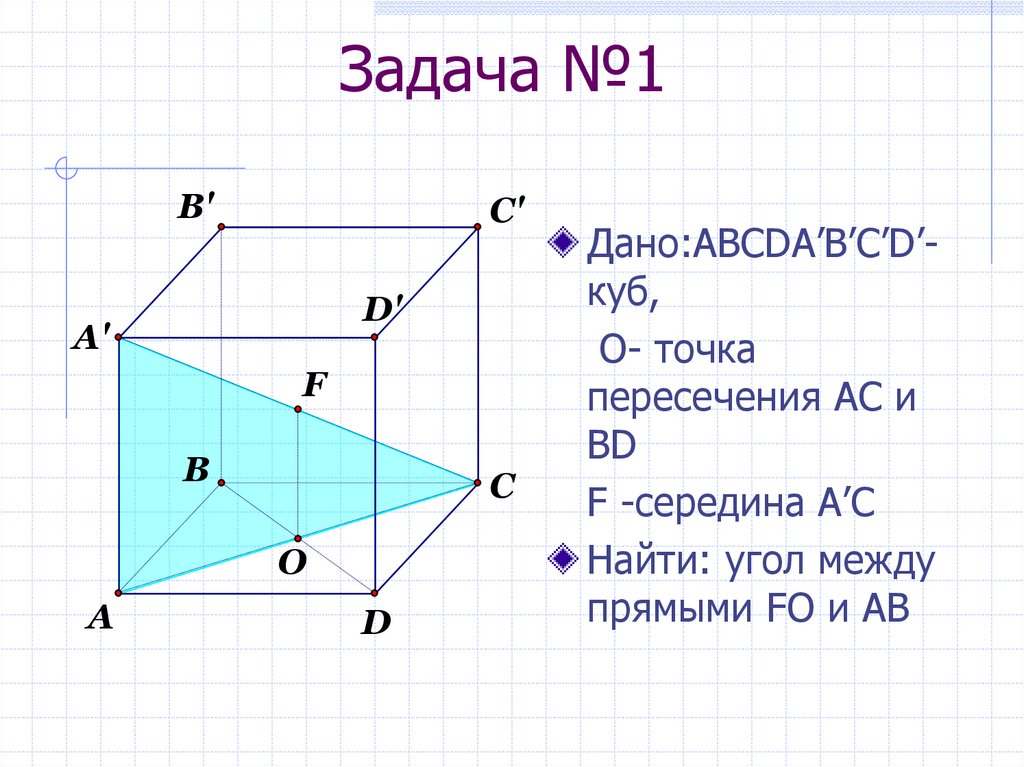
8. Задача №1

B'
C'
D'
A'
F
B
C
О
A
D
Дано:ABCDA’B’C’D’куб,
О- точка
пересечения AC и
BD
F -середина А’С
Найти: угол между
прямыми FO и АВ

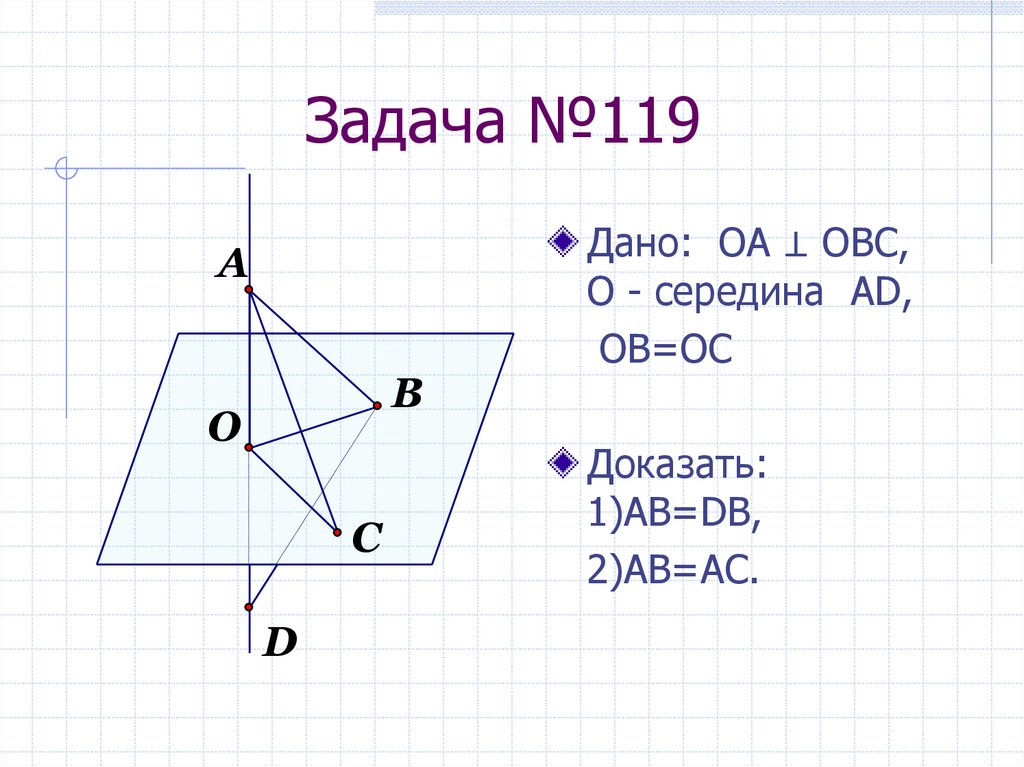
9. Задача №119

A
B
O
C
D
Дано: ОА ⊥ ОВС,
О - середина AD,
OB=OC
Доказать:
1)АВ=DB,
2)AB=AC.

10. Верны ли утверждения:

Прямая перпендикулярна плоскости,
если она перпендикулярна какой–
нибудь прямой, лежащей в этой
плоскости?
Прямая перпендикулярна плоскости,
если она перпендикулярна
параллельным прямым?

11.

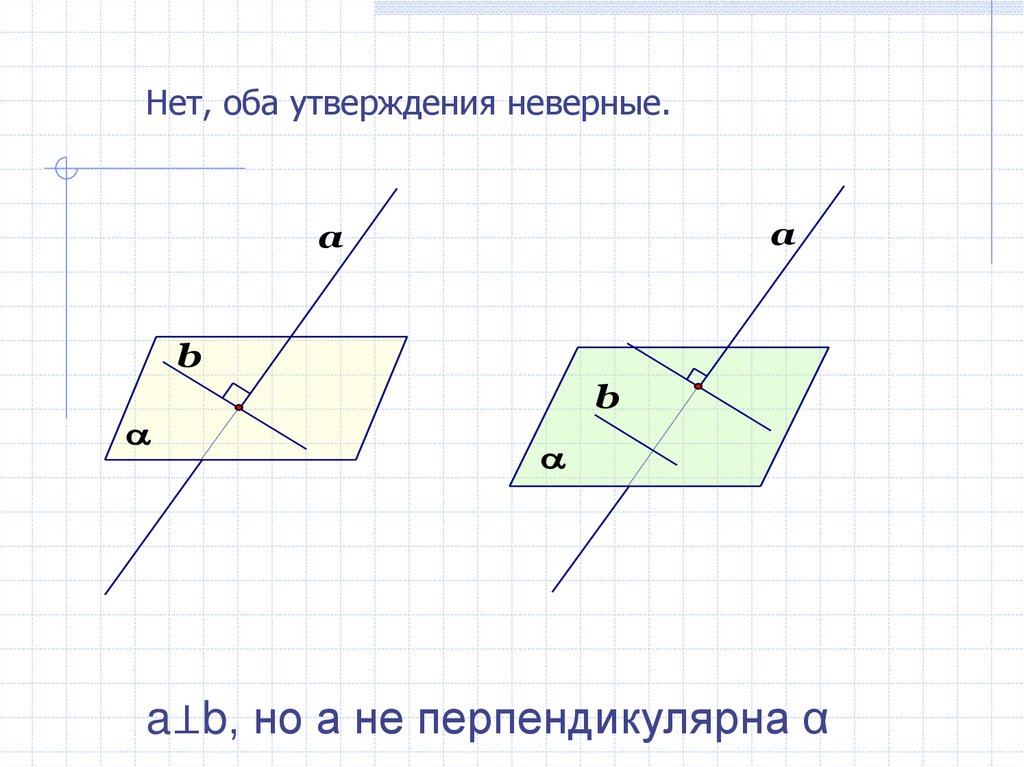
Нет, оба утверждения неверные.
a
a
b
b
a⊥b, но а не перпендикулярна α

12. Признак перпендикулярности прямой и плоскости

Если прямая перпендикулярна к двум
пересекающимся прямым, лежащим в
плоскости, то она перпендикулярна
этой плоскости.

13.

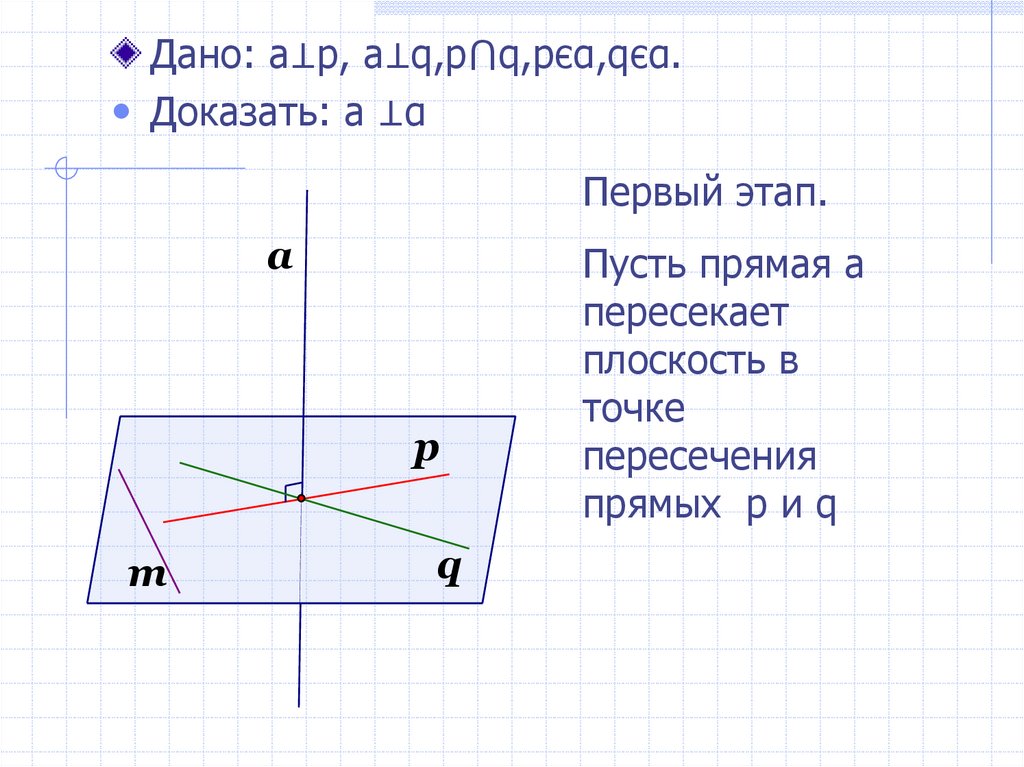
Дано: a⊥p, a⊥q,p⋂q,pєα,qєα.
• Доказать: а ⊥α
Первый этап.
a
p
m
q
Пусть прямая а
пересекает
плоскость в
точке
пересечения
прямых p и q

14.

A
a
q
p
O
m
L
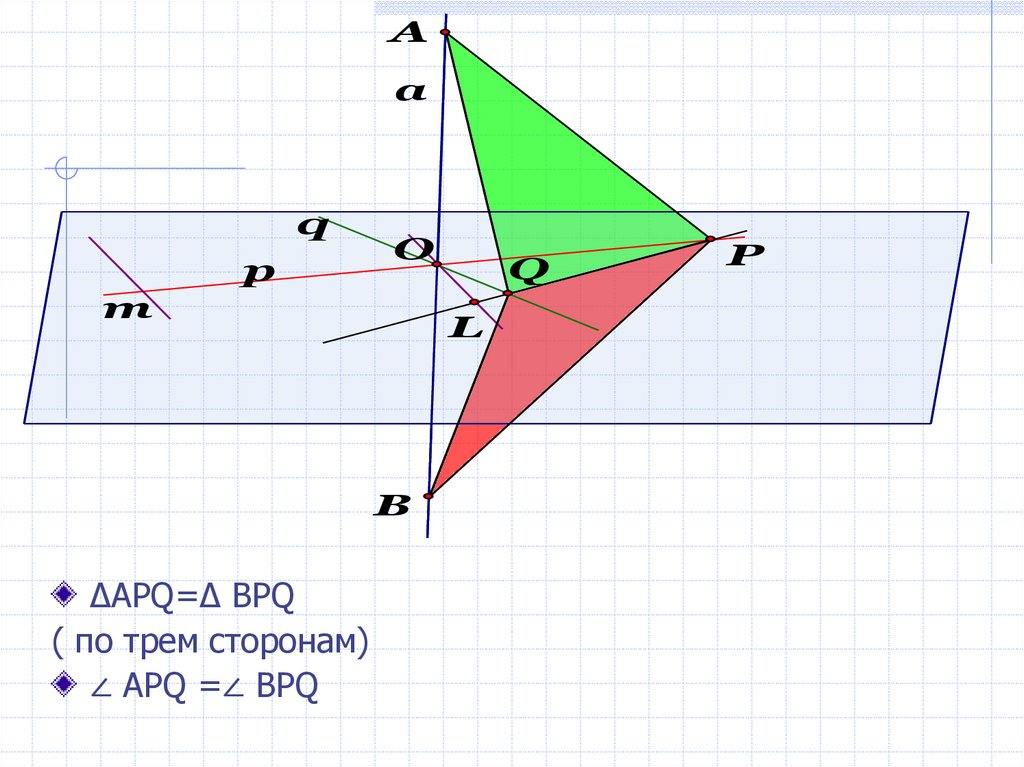
B
∆APQ=∆ BPQ
( по трем сторонам)
∠ APQ =∠ ВPQ
Q
P

15.

A
a
q
p
O
m
Q
P
L
B
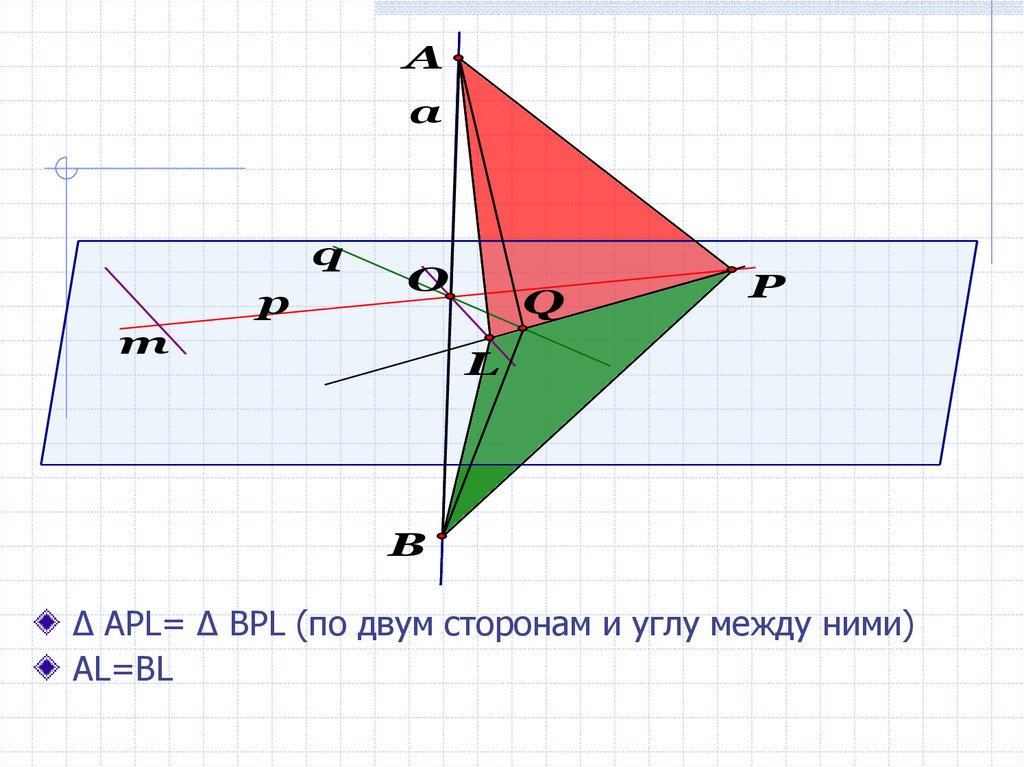
∆ APL= ∆ BPL (по двум сторонам и углу между ними)
AL=BL

16.

A
a
q
p
O
m
Q
L
B
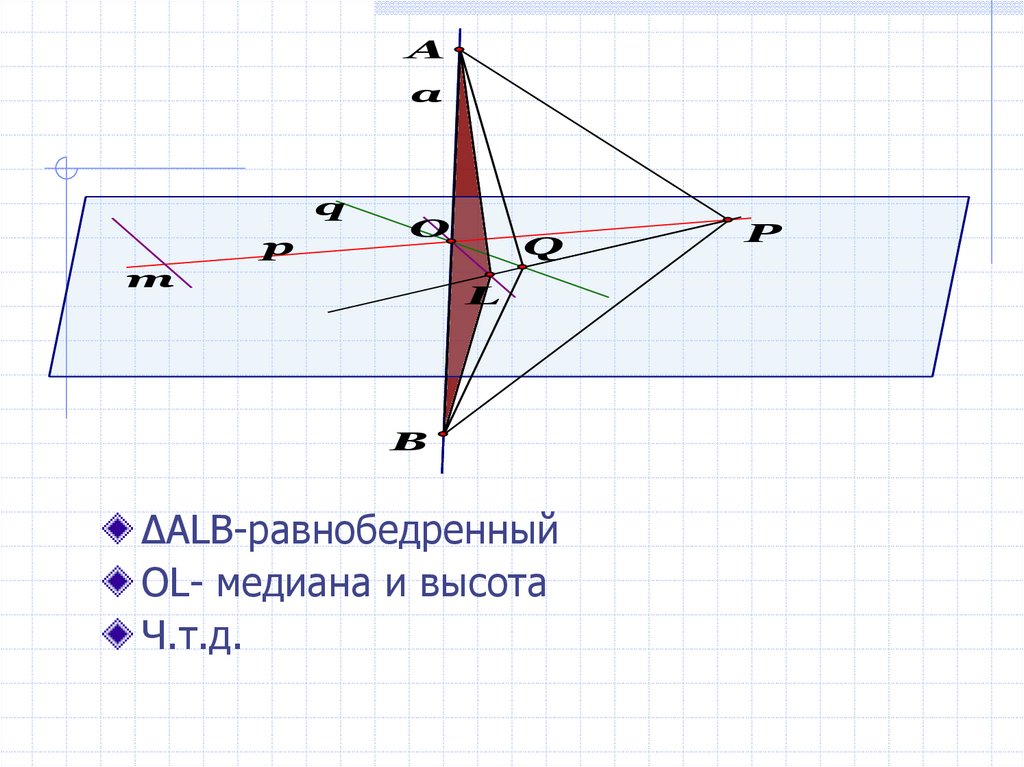
∆ALB-равнобедренный
OL- медиана и высота
Ч.т.д.
P

17.

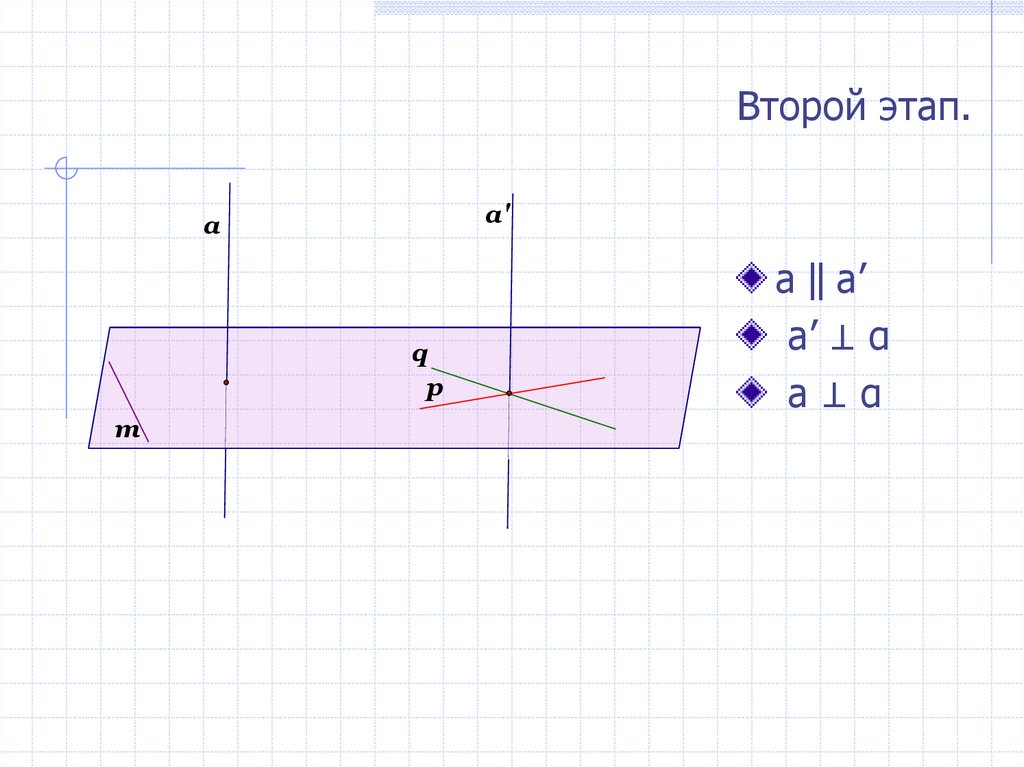
Второй этап.
a'
a
q
p
m
a ‖ a’
a’ ⊥ α
a⊥α

18. Проверка перпендикулярности осветительных столбов

19. № 128

M
B
C
O
A
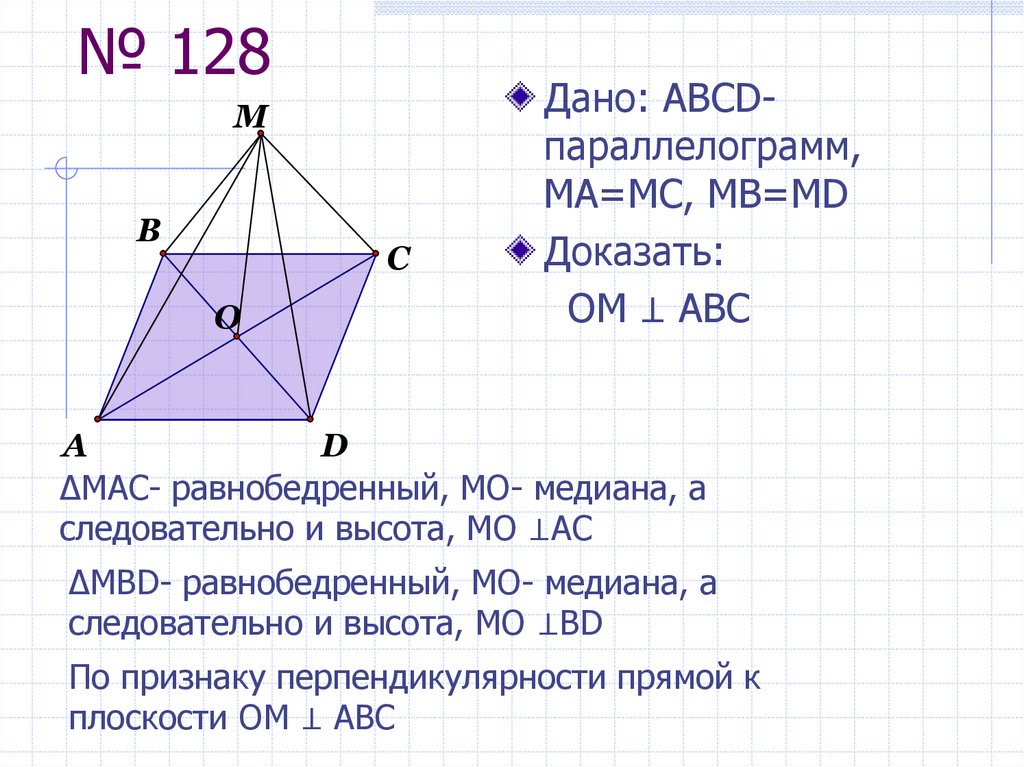
Дано: АBCDпараллелограмм,
MA=MC, MB=MD
Доказать:
ОМ ⊥ АВС
D
∆МАС- равнобедренный, МО- медиана, а
следовательно и высота, МО ⊥АС
∆МBD- равнобедренный, МО- медиана, а
следовательно и высота, МО ⊥BD
По признаку перпендикулярности прямой к
плоскости ОМ ⊥ АВС

20. Прямая а проходит через центр круга. Можно ли утверждать, что прямая а перпендикулярна кругу, если

1.она перпендикулярна диаметру
2.двум радиусам
3.двум диаметрам

21. Проверка вертикальности

22. Домашнее задание

П .15-17 №124, 126

23. До новых встреч!