Similar presentations:
Презентация лекции 10 ВМ в МКЭ
1. Лекция 10. Вариационный принцип Лагранжа в МКЭ. Плоская задача. Треугольный конечный элемент.
Вариационный принцип (и уравнение)Лагранжа может быть сформулирован
следующим образом: из множества
кинематически допустимых перемещений,
перемещения, действительно имеющие
место, сообщают потенциальной энергии
упругой
системы
(Э)
минимальное
значение. Соответствующее уравнение
записывается в виде:
dЭ=0
(1)
2.
Полная потенциальная энергия упругой системы Э может бытьразделена на две части, одна из которых соответствует работе
(энергии деформации) внутренних сил W, а другая определяется
работой приложенных (в частности внешних A) сил.
После разбиения области на элементы это равенство должно
быть записано в виде суммы
s
Э W A
r
r
r 1
где s – общее количество конечных элементов.
Энергия деформации бесконечно малого объема d U в
случае статического приложения внешних сил и наличия
вынужденных деформаций может быть вычислена по
формуле:
dW r
1 T
2
(3)
3. Связь вектора деформации с вектором перемещений и напряжений (плоская задача)
xy ,
xy
u
Z
v
B Z,
T
D DB Z
T
x
u
,
x
y
v
,
x
1
x
E
y
1 2
0
xy
1
E
D
2
1
0
1
0
xy
1
0
0
0
1
2
u v
,
y x
0 x
0 y ,
1
2 xy
4.
5. Вариации работы внешних сил и потенциальной энергии
A ( z )T P r ,T
W ( ) dV
Vr
Символ означает вариацию, т.е. возможное изменение,
P r - вектор узловой нагрузки.
Z- вектор узловых перемещений. Т.к. вариация полной энергии в
стационарном состоянии должна быть равна нулю, т.е. δЭ=δА-δW=0, то
вектор внешней нагрузки имеет вид:
P r ( BT DBdV ) z r , P r K r z r , K r BT DBdV
Vr
Vr
Величина Кr – представляет собой реакции
перемещений, т.е. матрицу жесткости системы.
от
единичных
6. Матрица жесткости для r-го элемента при постоянной толщине h и площади A
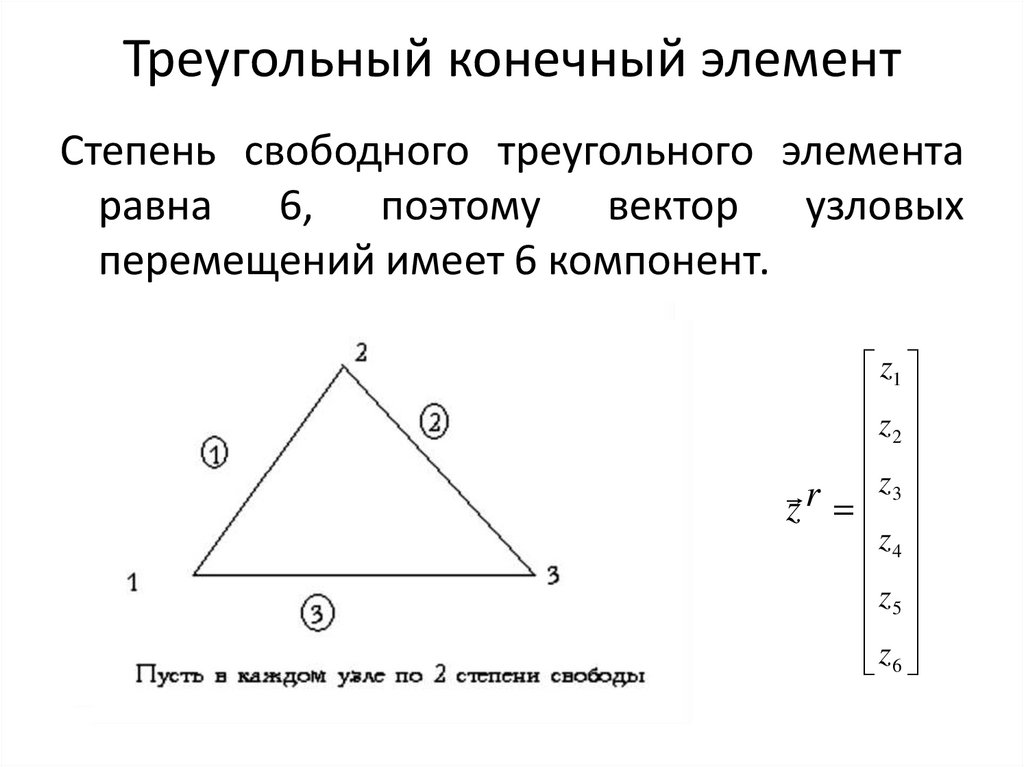
7. Треугольный конечный элемент
Степень свободного треугольного элементаравна 6, поэтому вектор узловых
перемещений имеет 6 компонент.
z1
z2
z r z3
z
4
z5
z 6
8. Матрица жесткости для треугольного элемента
9. Тестовые вопросы
1. Связь вектора деформации с векторомперемещений и напряжений (плоская
задача)
2. Формирование матрицы жесткости для
плоской задачи
3. Формирование матрицы жесткости для
треугольного элемента
4. Формирование
матрицы
Д,
определяющей модули системы



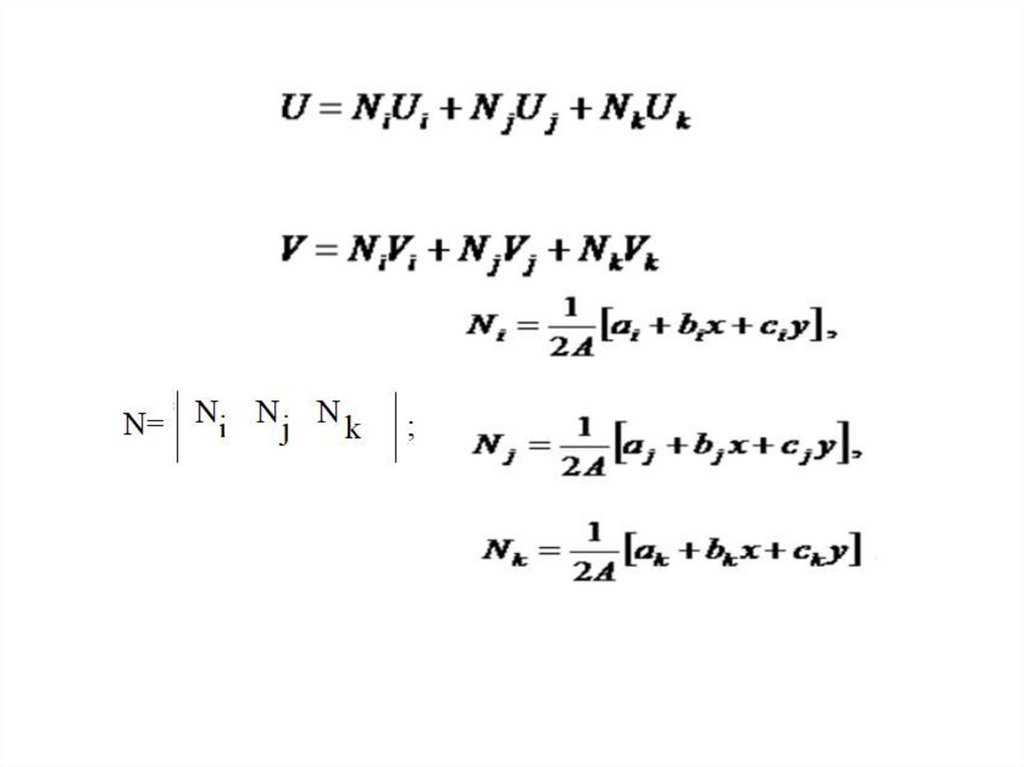




 Construction
Construction








