Vector_product

1.

Dot product and
Cross product
to turn math into the world’s most engaging sport
- starting where it was born
Uzbekistan, 12th November 2025

2.

Learning objectives
•Understand the distinction between scalar and vector products in terms of result (scalar vs vector)
and geometric meaning.
•Recognize how vector orientation influences the outcomes of dot and cross products.
•Interpret the dot product as a measure of directional alignment and the cross product as a
measure of perpendicular interaction.

3.

Learning objectives
•Compute the scalar (dot) product using algebraic and magnitude–angle formulations.
•Compute the vector (cross) product using determinant and component methods.
•Apply properties of dot and cross products (commutativity, distributivity, anti-commutativity where
applicable, scalar multiplication rules).
•Use vector products to determine angles, magnitudes, and orthogonality conditions.

4.

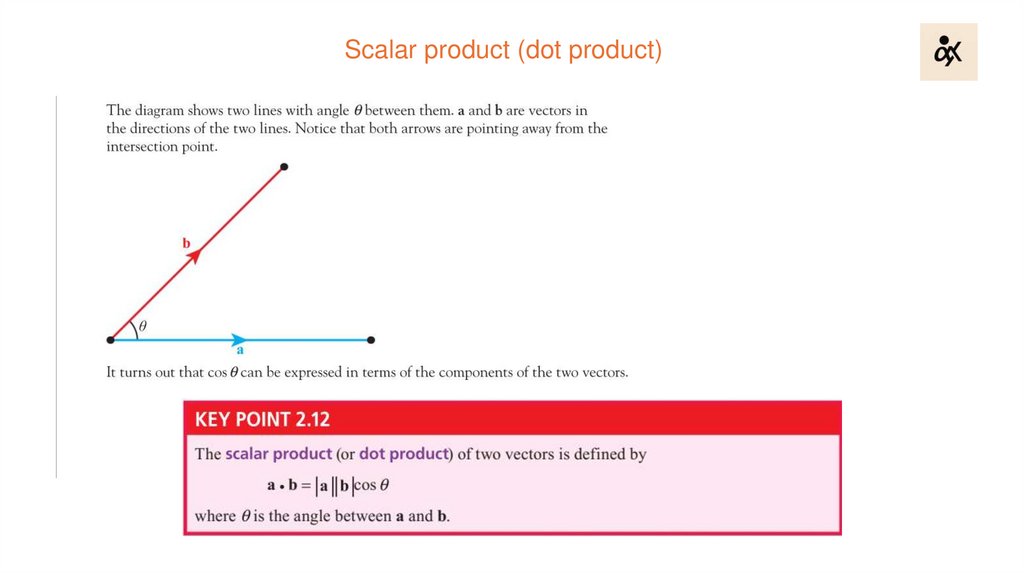
Scalar product (dot product)

5.

Examples

6.

Another form of a product
Notice that the scalar product is a number (scalar).

7.

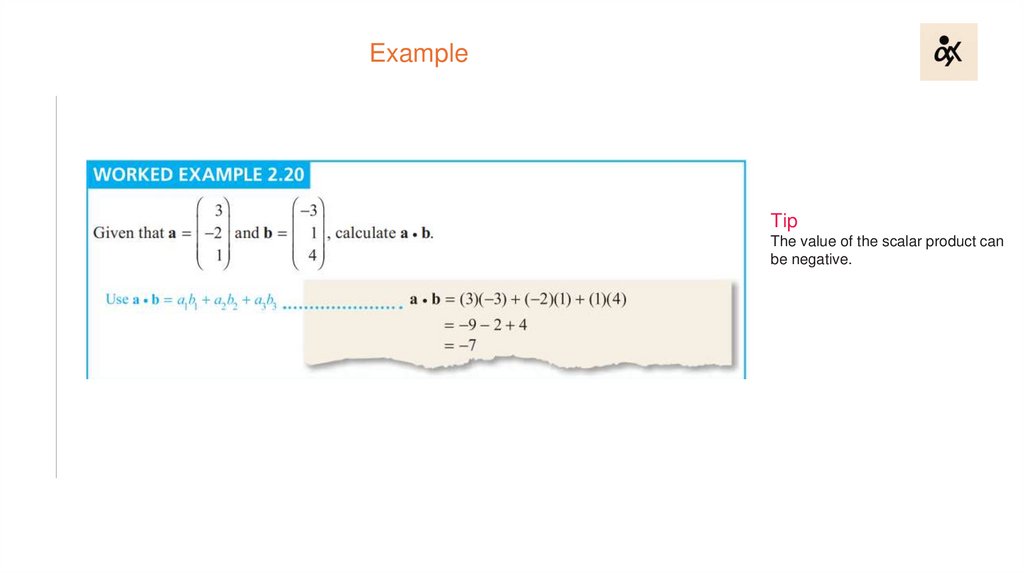
Example
Tip
The value of the scalar product can
be negative.

8.

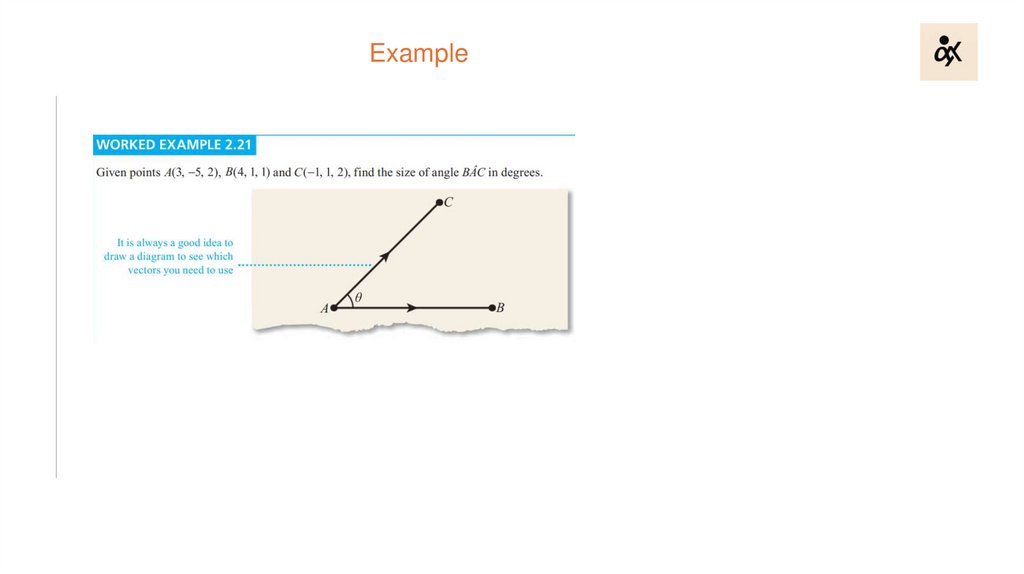
Another form of a product
Calculating the angle between two vectors given in component form.

9.

Example

10.

Examples

11.

Examples
Two further important properties of the scalar product concern perpendicular and
parallel vectors. They are derived using the facts that cos 90° = 0, cos 0° = 1 and
cos180° = -1.

12.

Now let’s dive in to solve practice questions
Someone who fights for tomorrow lives in a today !
Dr. Bret Stenbarger