Similar presentations:
тригонометрические функции 10
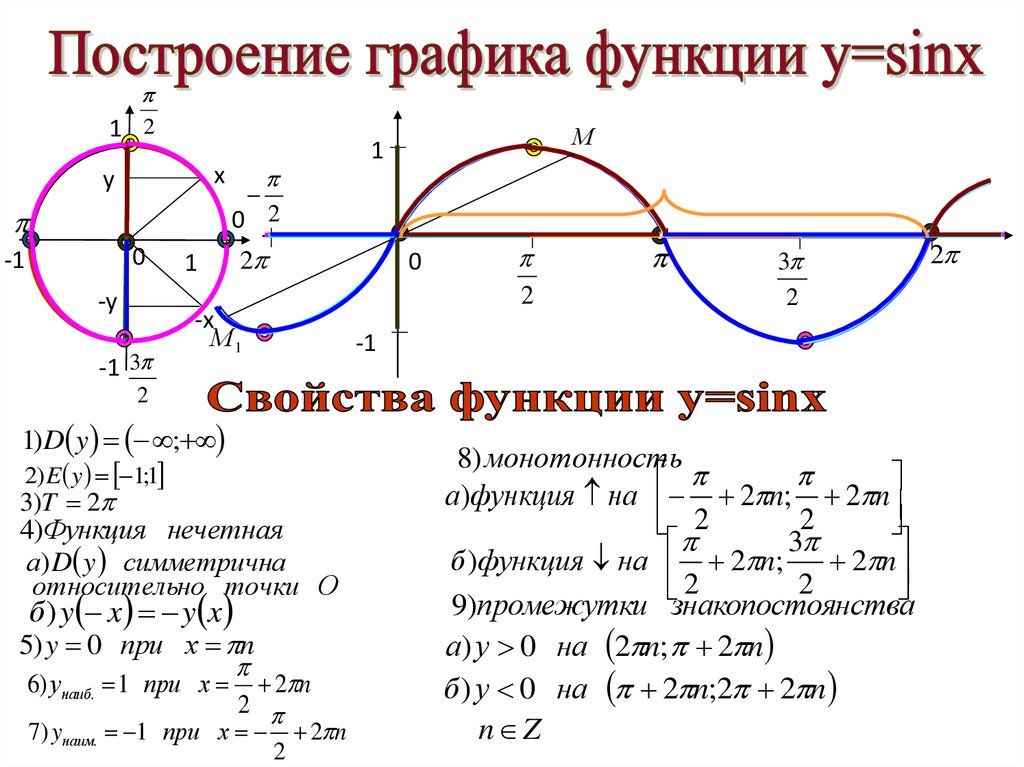
1. Тригонометрические функции, их свойства и графики
2.
1 2x
y
М
1
0 2
0
-1
-y
-1 3
1
2
0
-x
М1
2
3
2
-1
2
1) D y ;
2) E y 1;1
3)T 2
4)Функция нечетная
а) D y симметрична
относительно точки О
б ) y x y x
5) y 0 при х n
6) унаиб. 1 при х
2 n
2
7) yнаим. 1 при х
2
2 n
8) монотонность
а)функция на 2 n; 2 n
2
2
3
б )функция на 2 n;
2 n
2
2
9)промежутки знакопостоянства
а) у 0 на 2 n; 2 n
б ) у 0 на 2 n;2 2 n
n Z
2
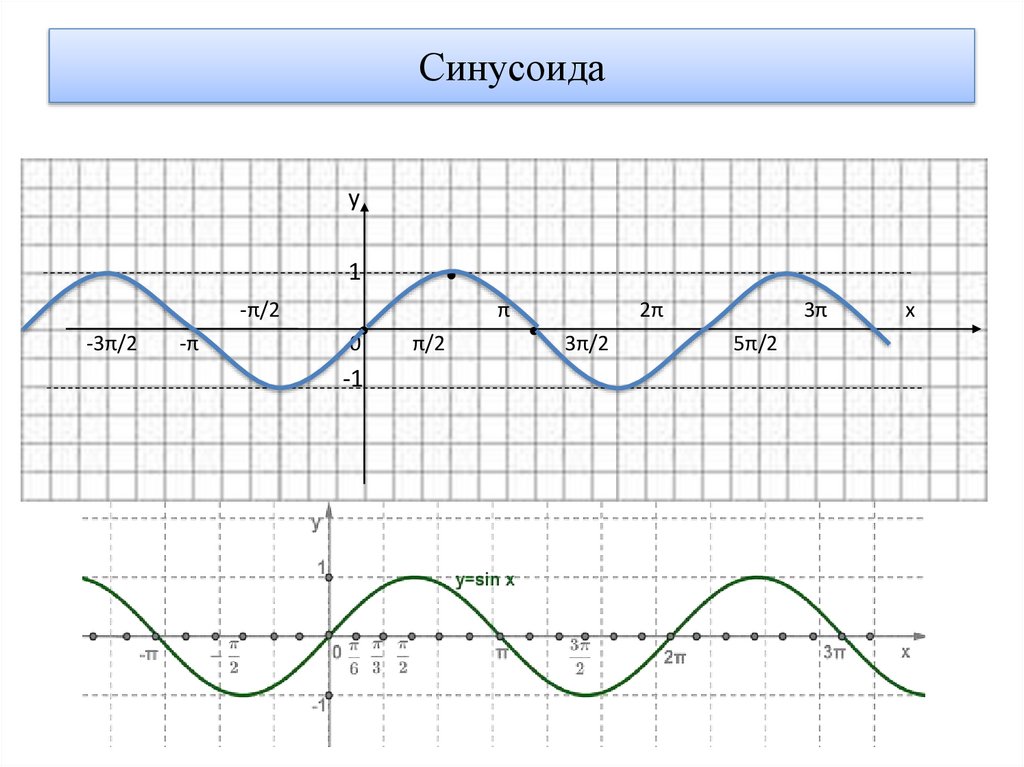
3. Синусоида
у1
-π/2
-3π/2
-π
π
0
-1
π/2
2π
3π/2
3π
5π/2
х
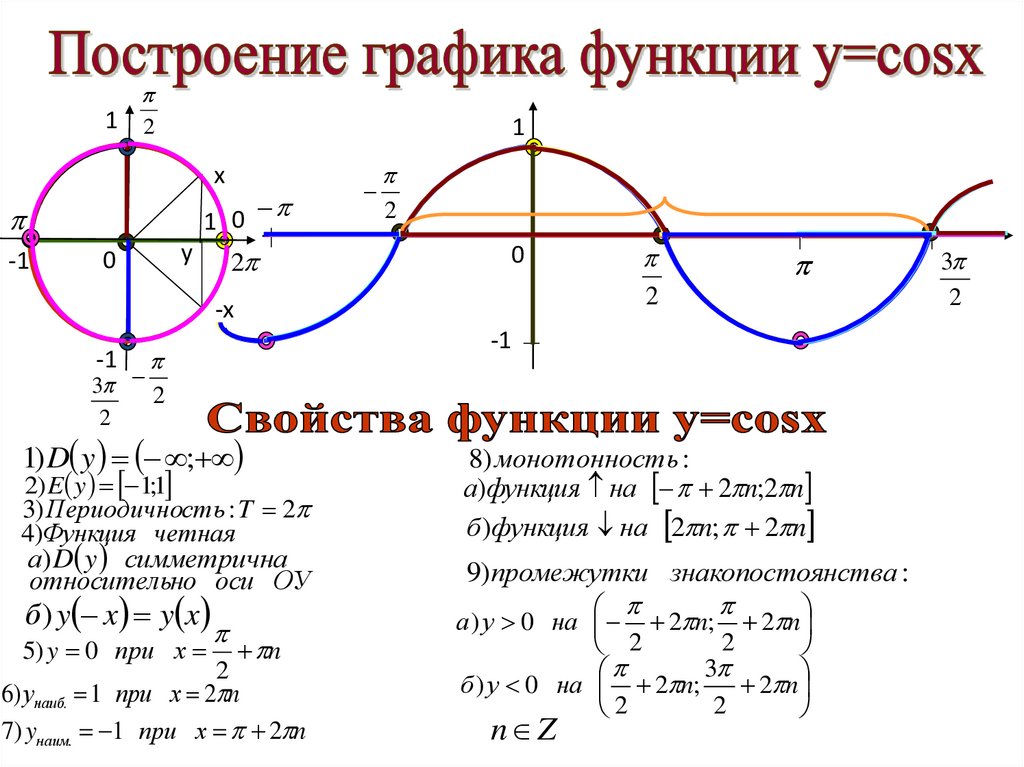
4.
1 21
x
1 0
-1
y
0
2
2
0
-x
-1
2
-1
3 2
2
1) D y ;
2) E y 1;1
3) Периодичность : T 2
4)Функция четная
8) монотонность :
а)функция на 2 n;2 n
б )функция на 2 n; 2 n
б) y x y x
9)промежутки знакопостоянства :
а ) у 0 на 2 n; 2 n
а) D y симметрична
относительно оси ОУ
5) y 0 при х
n
2
6) унаиб. 1 при х 2 n
7) yнаим. 1 при х 2 n
2
2
3
б ) у 0 на 2 n;
2 n
2
2
n Z
3
2
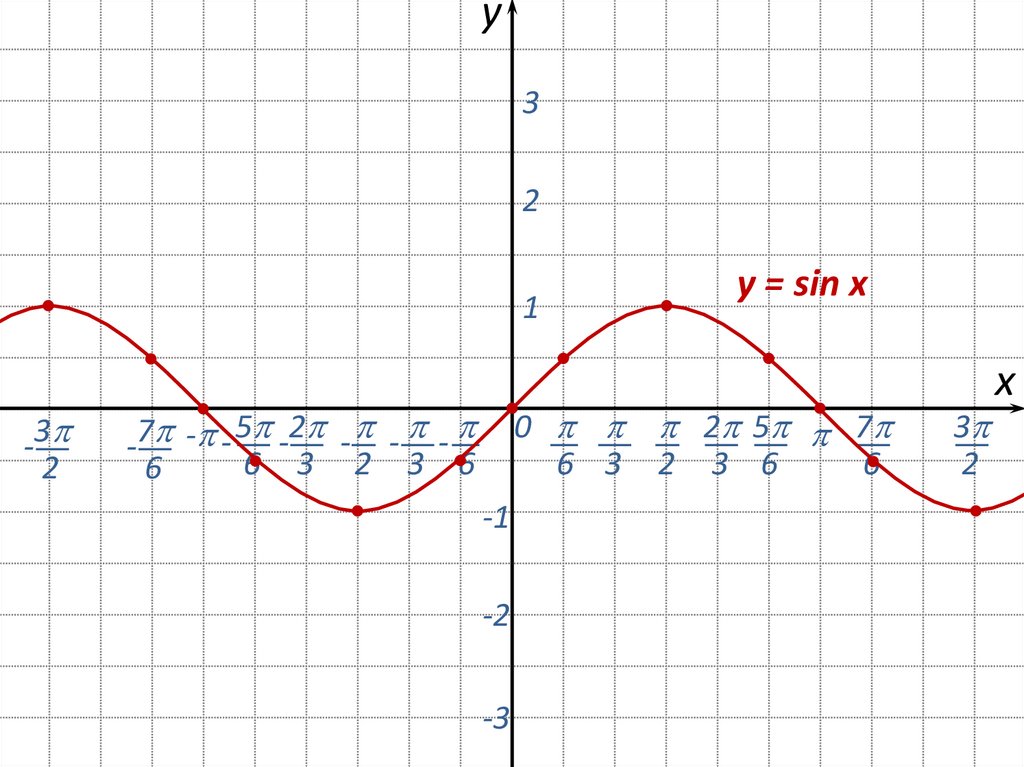
5.
y3
2
y = sin x
1
-3
2
5 -2 - - -
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2
х
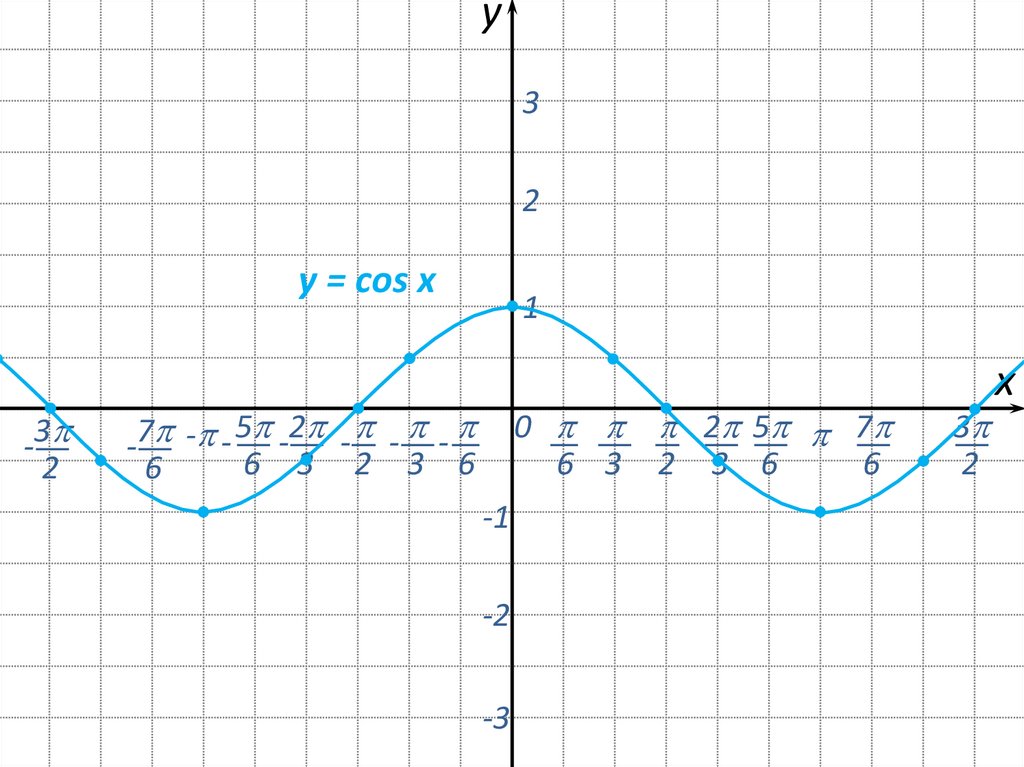
6.
y3
2
y = соs x
-3
2
1
5 -2 - - -
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2
х
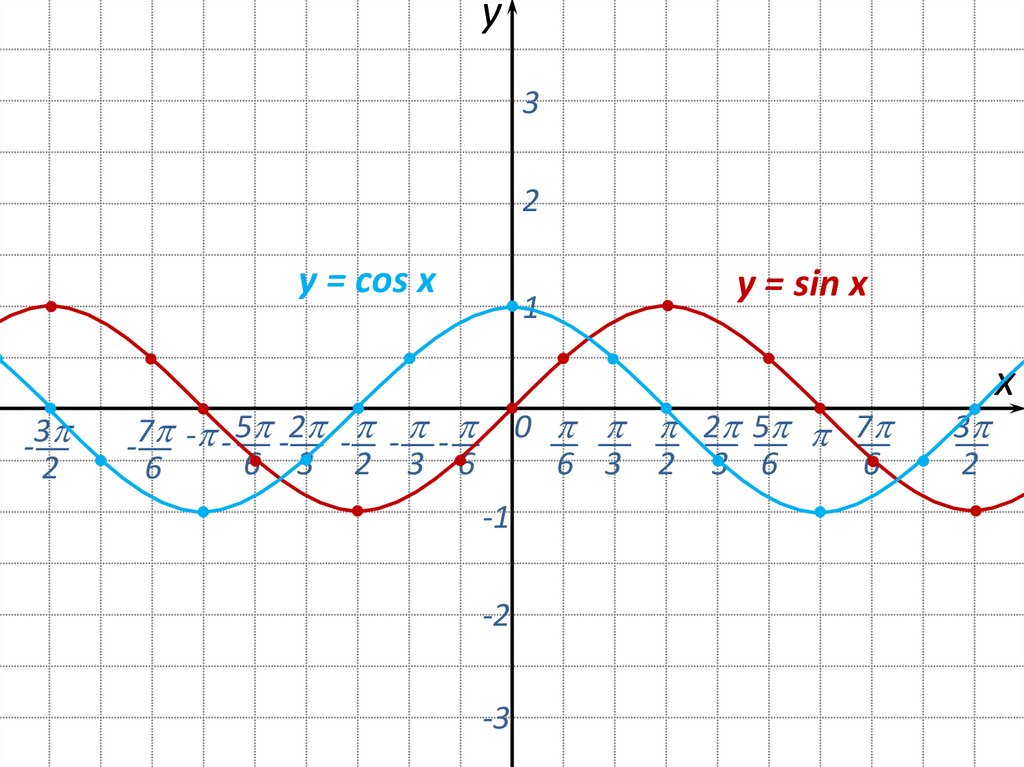
7.
y3
2
y = соs x
-3
2
y = sin x
1
5 -2 - - -
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2
х
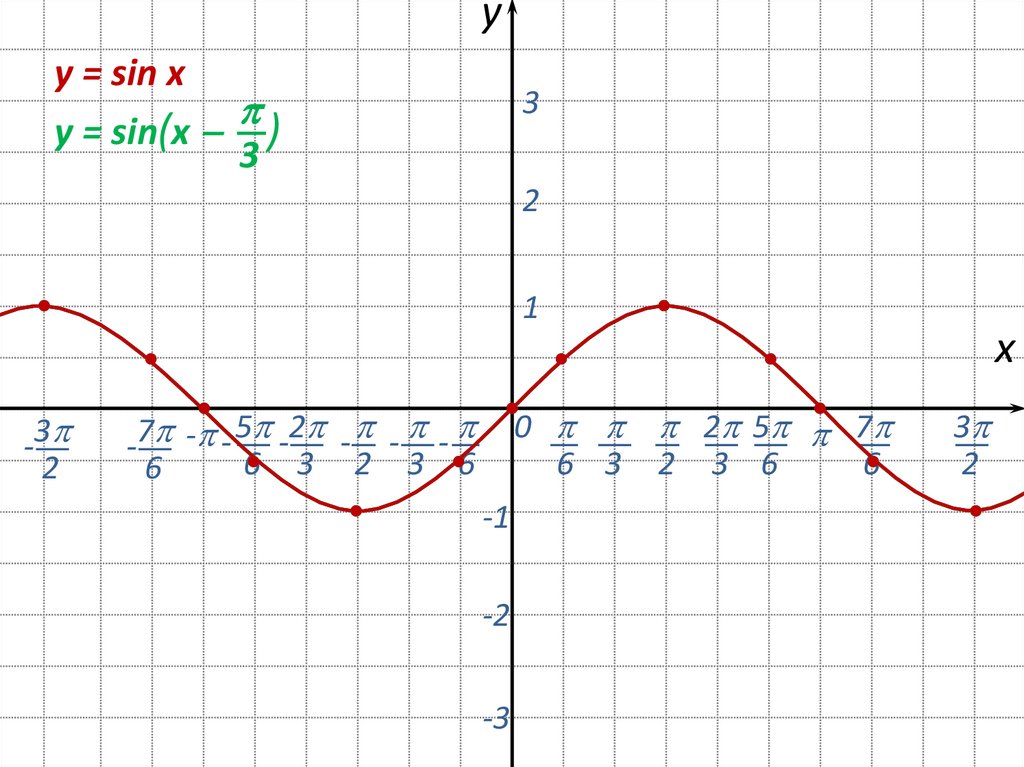
8.
yy = sin x
y = sin(x )
3
3
2
1
х
-3
2
5 -2 - - -
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2
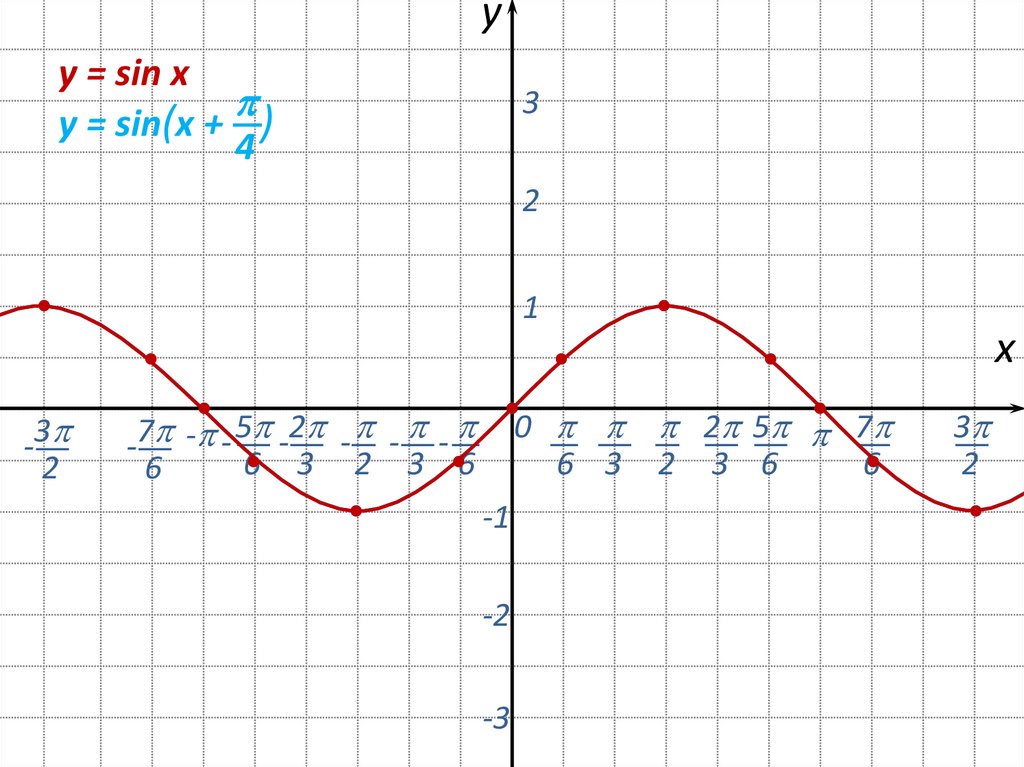
9.
yy = sin x
y = sin(x + )
4
3
2
1
х
-3
2
5 -2 - - -
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2
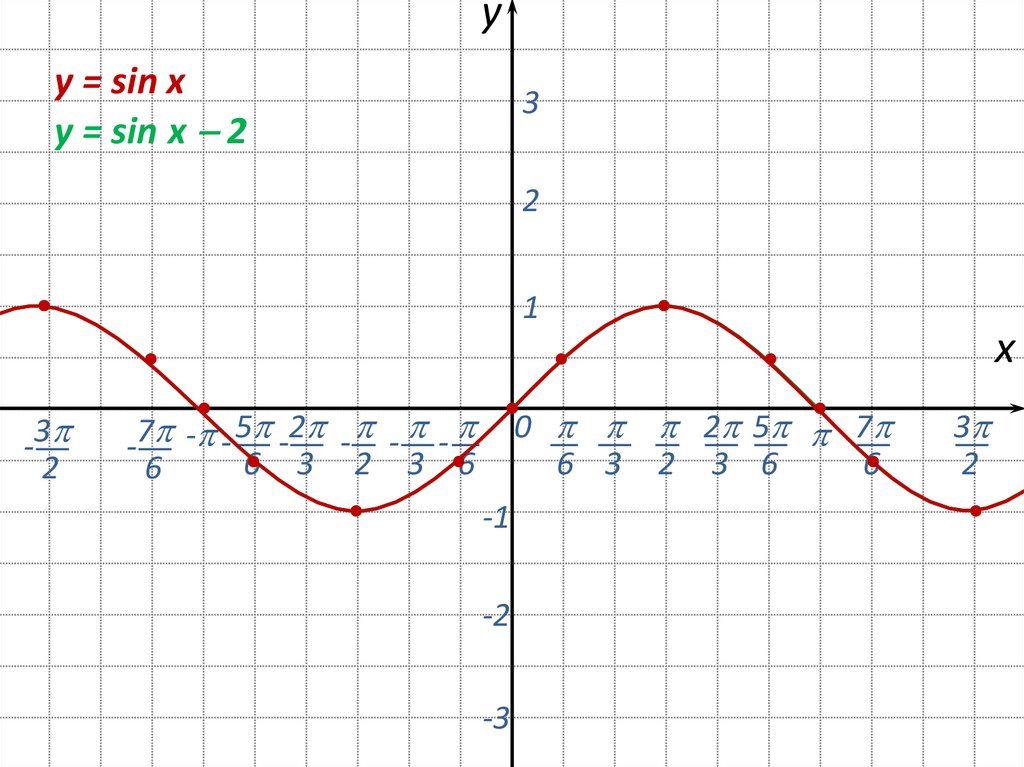
10.
yy = sin x
y = sin x 2
3
2
1
х
-3
2
5 -2 - - -
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2
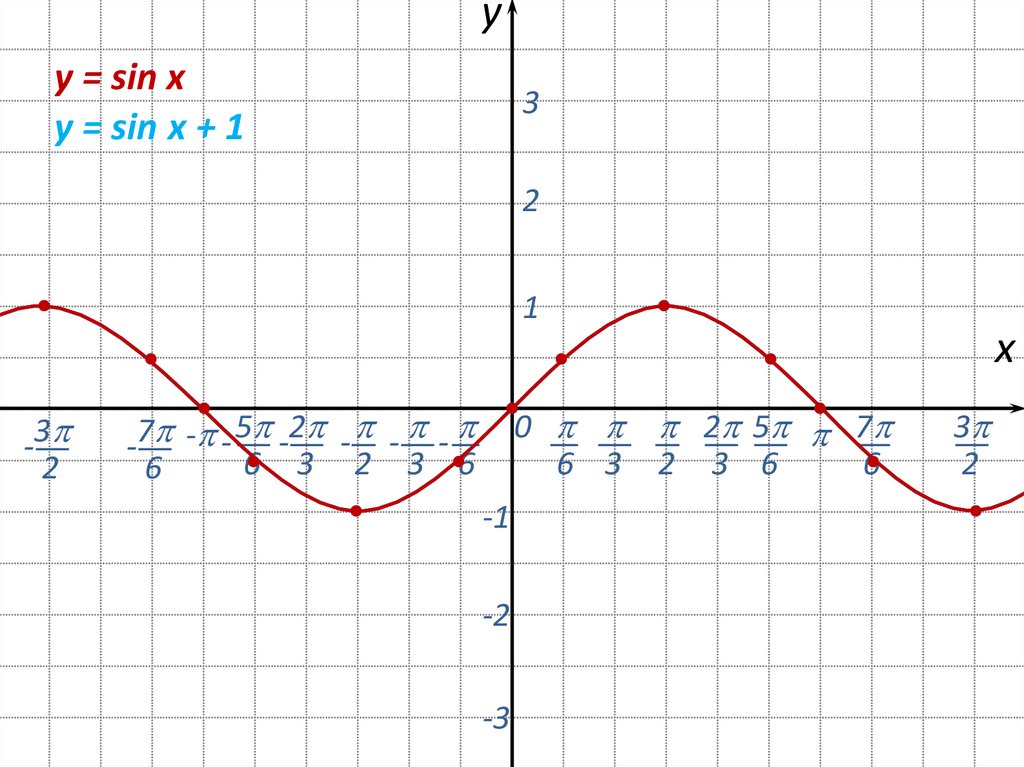
11.
yy = sin x
y = sin x + 1
3
2
1
х
-3
2
5 -2 - - -
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2
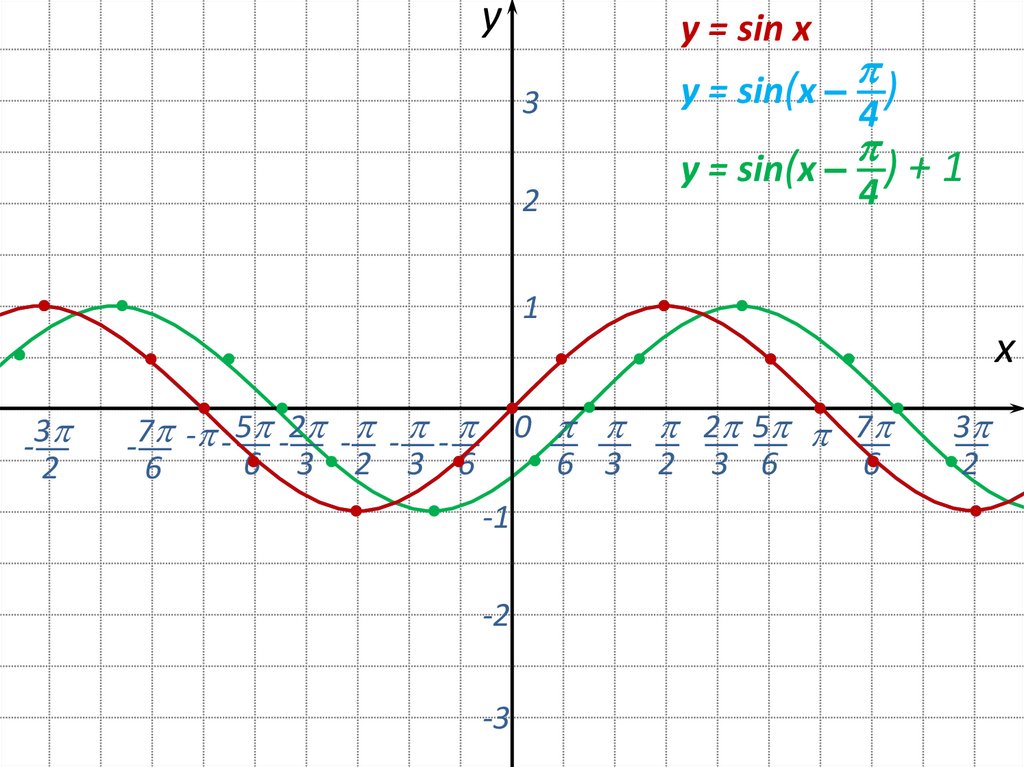
12.
yy = sin x
y = sin(x – )
4
y = sin(x – ) + 1
4
3
2
1
х
-3
2
5 -2 - - -
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2
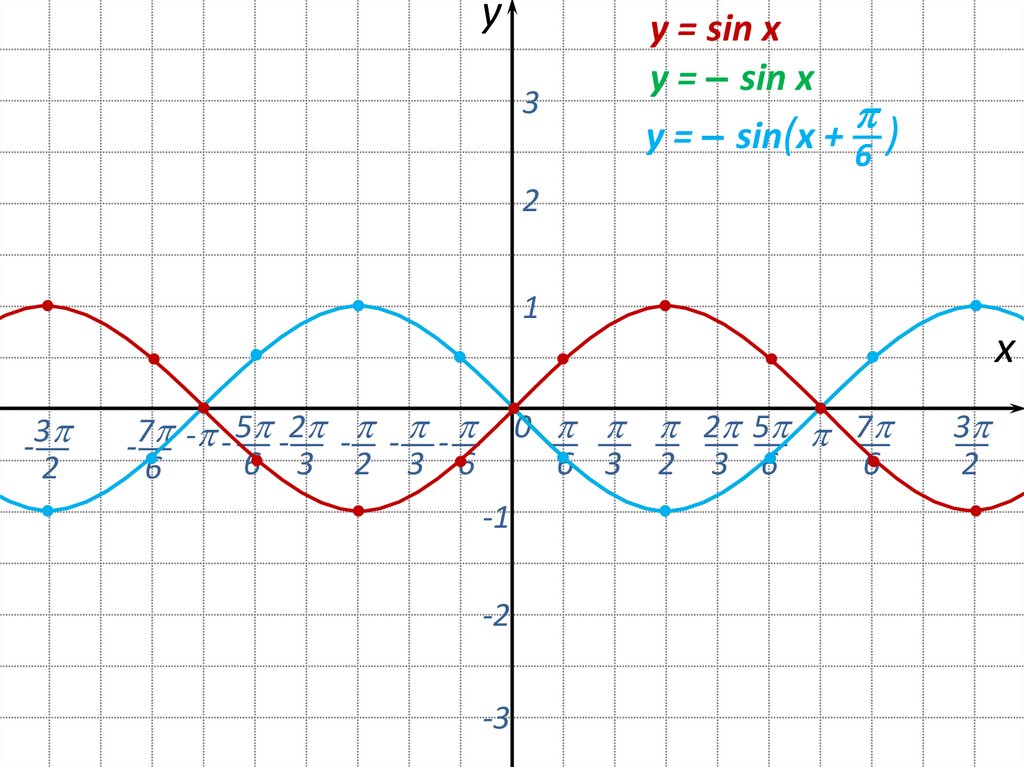
13.
y3
y = sin x
y = – sin x
y = – sin(x + 6 )
2
1
х
-3
2
5 -2 - - -
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2
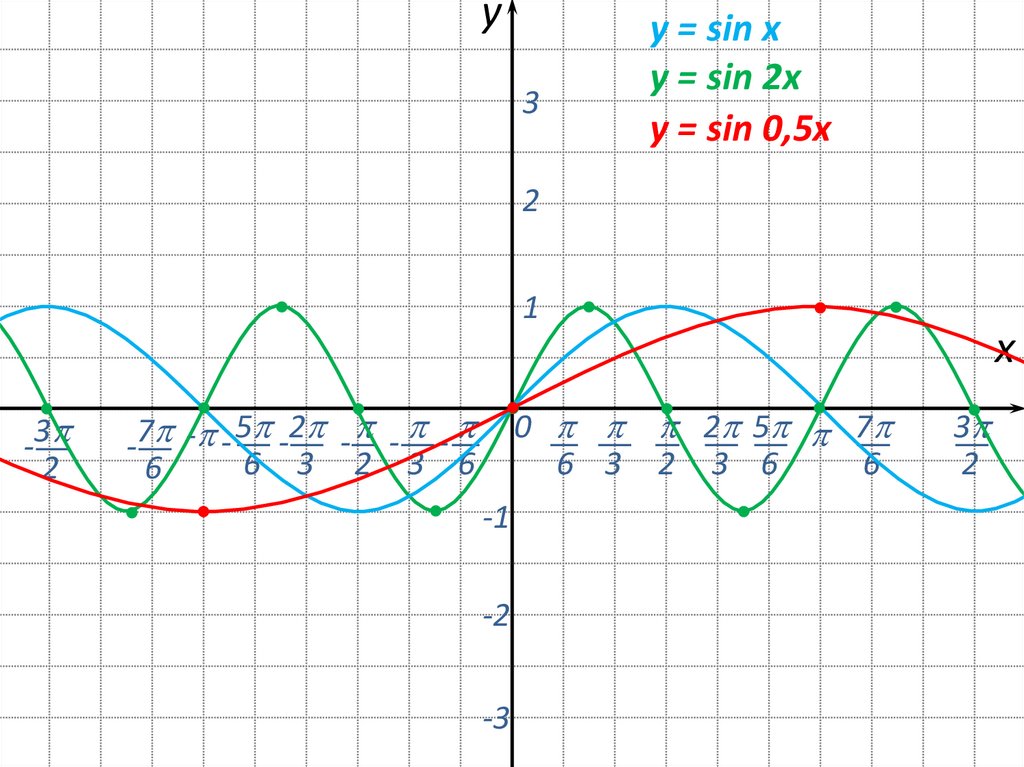
14.
y3
y = sin x
y = sin 2x
y = sin 0,5x
2
1
х
-3
2
5 -2 - - -
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2
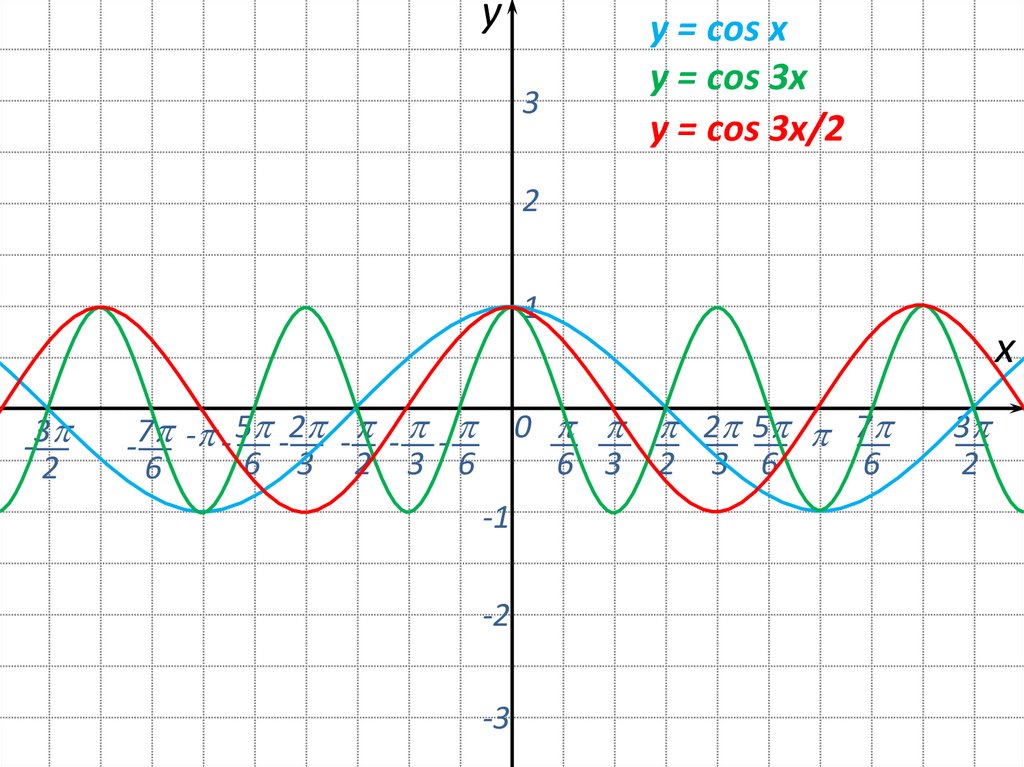
15.
y3
y = соs x
y = соs 3x
y = соs 3x/2
2
1
х
-3
2
5 -2 - - -
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2
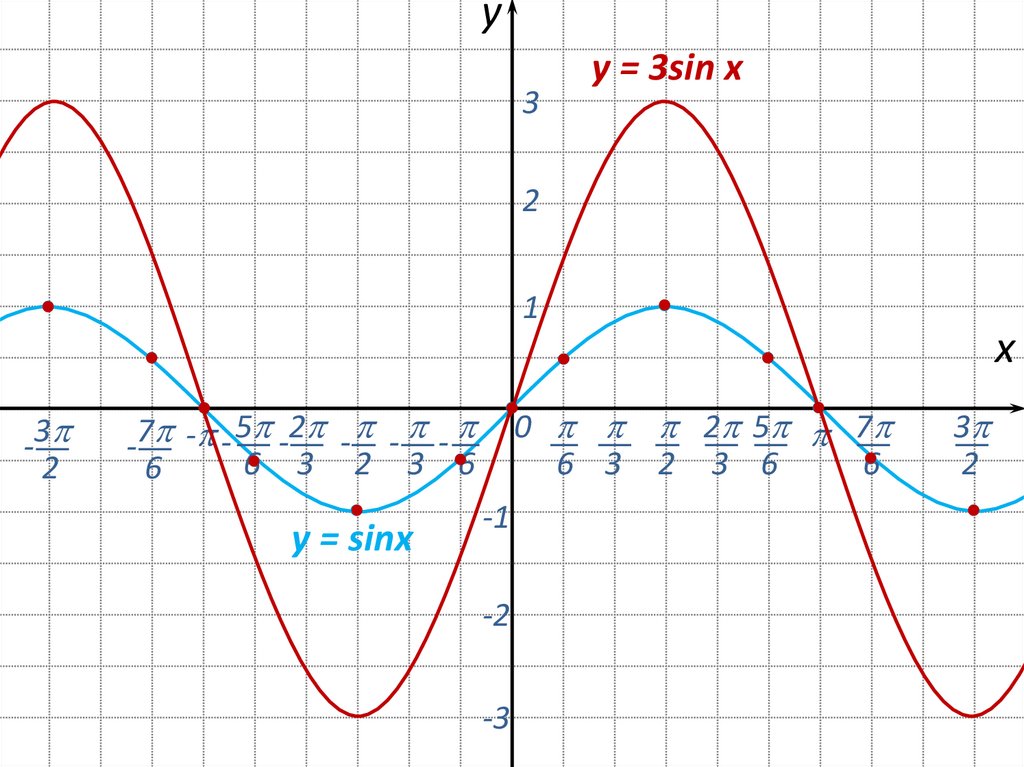
16.
y3
y = 3sin x
2
1
х
-3
2
5 -2 - - -
7
6 3 2 3 6
6
y = sinx
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2
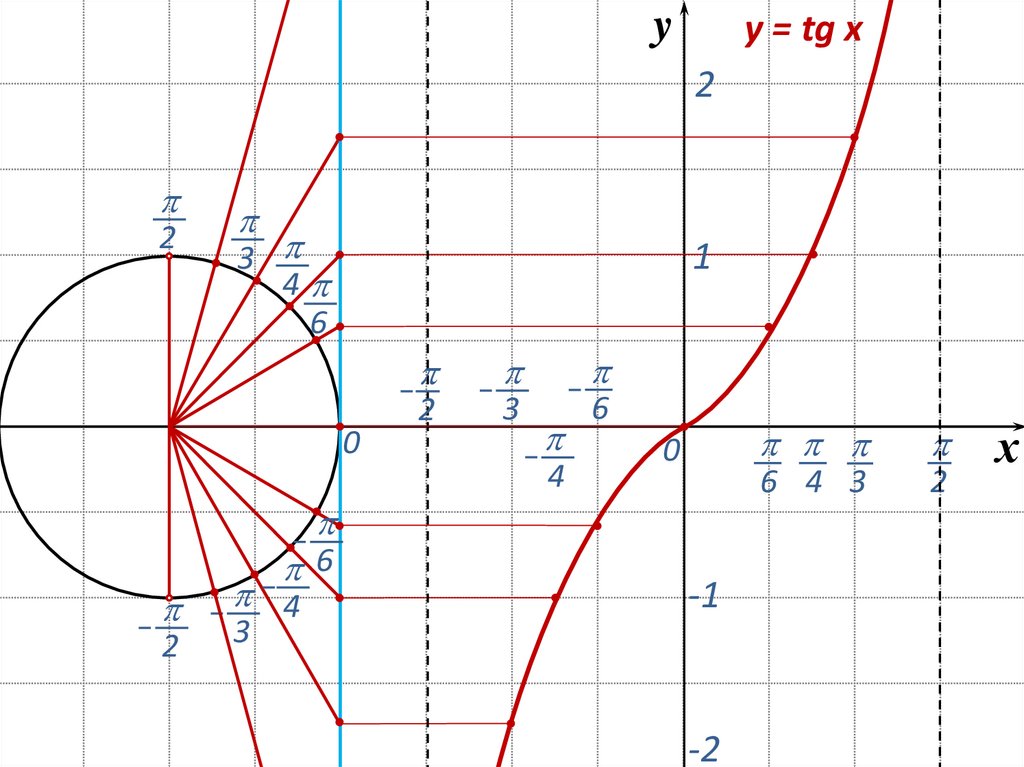
17.
yy = tg x
2
2
3
4
6
1
0
2
3
6
4
0
2
6
4
3
-1
-2
6 4 3
2
х
18. Свойства графика функции y=tg x
1. Область определения: x≠π/2+πn, n∈Z2. Множество значений: y∈(-∞;∞)
3.
4.
5.
6.
7.
8.
Функция периодическая Т=π
Функция нечетная
y=0, при x=πn, n∈Z
y>0, при x∈(πn; π/2+πn), n∈Z
y<0, при x∈(-π/2+πn; πn), n∈Z
Функция возрастает на интервалах: (-π/2+πn; π/2+πn), n∈Z
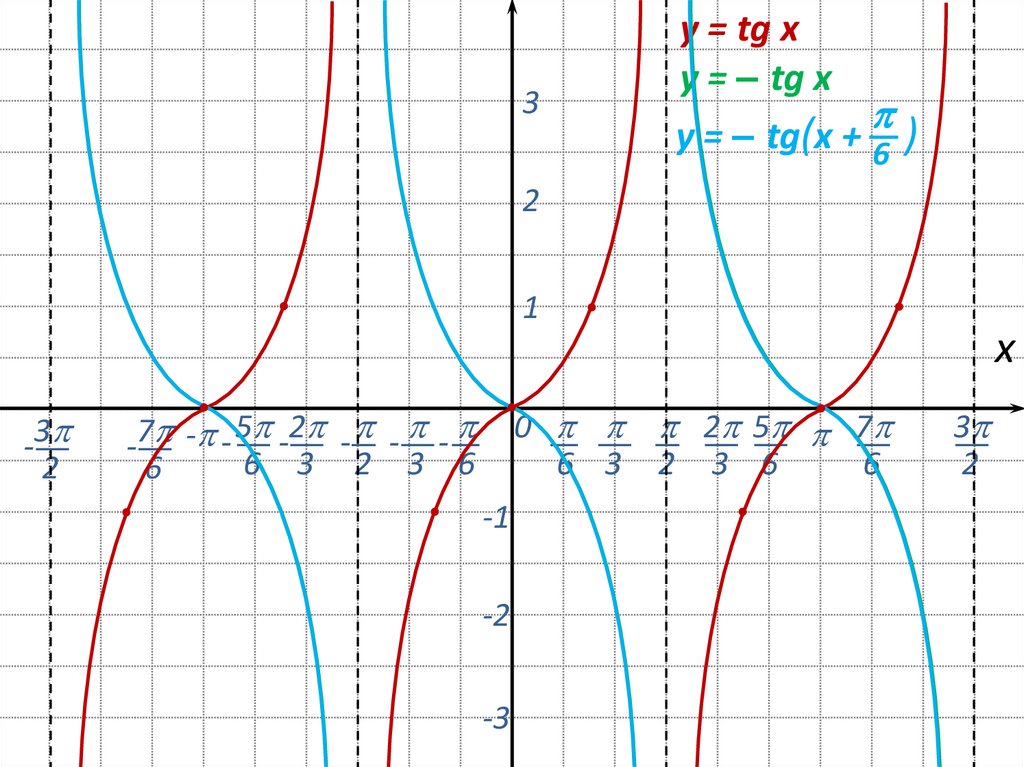
19.
y = tg xy = – tg x
y = – tg(x + 6 )
3
2
1
х
-3
2
5 -2 - - -
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2
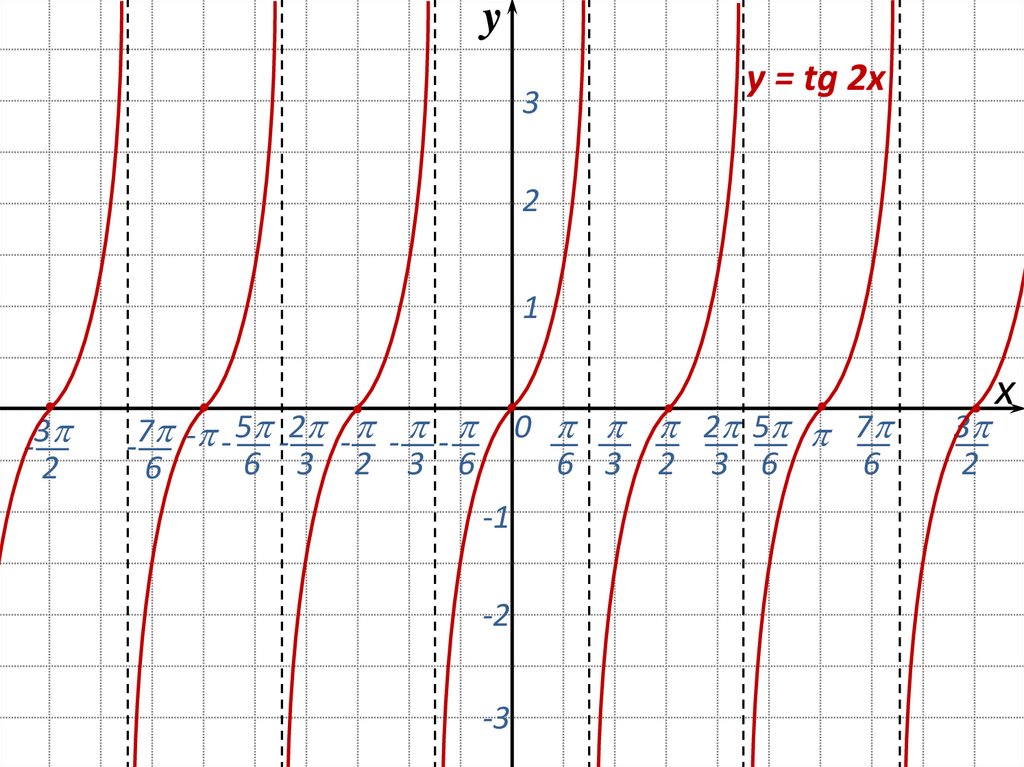
20.
yy = tg 2x
3
2
1
-3
2
5 -2 - - -
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2
х
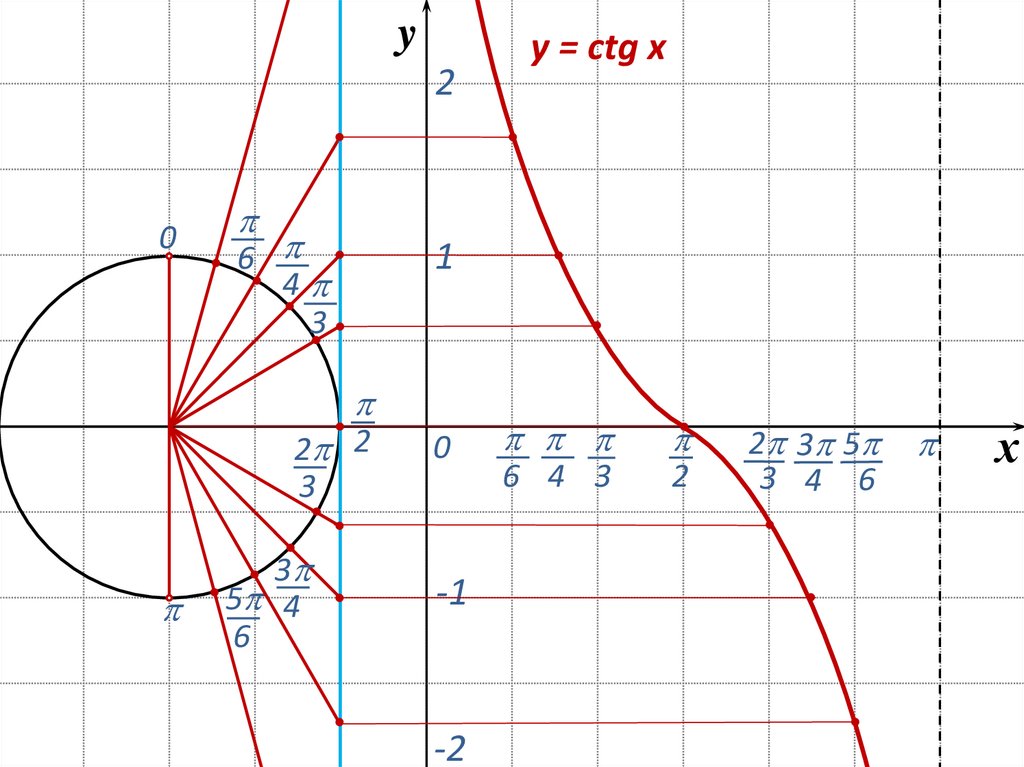
21.
y2
0
6
4
3
1
2 2
3
3
5 4
6
y = сtg x
0
-1
-2
6 4 3
2
2 3 5
3 4 6
х
22. Свойства графика функции y=ctg x
1. Область определения: x≠πn, n∈Z2. Множество значений: y∈(-∞;∞)
3.
4.
5.
6.
7.
8.
Функция периодическая T=π
Функция нечетная
y=0, при x=π/2+πn, n∈Z
y>0, при x∈(0+πn; π/2+πn), n∈Z
y<0, при x∈(-π/2+πn; 0+πn), n∈Z
Функция убывает на интервалах (πn; π+πn), n∈Z
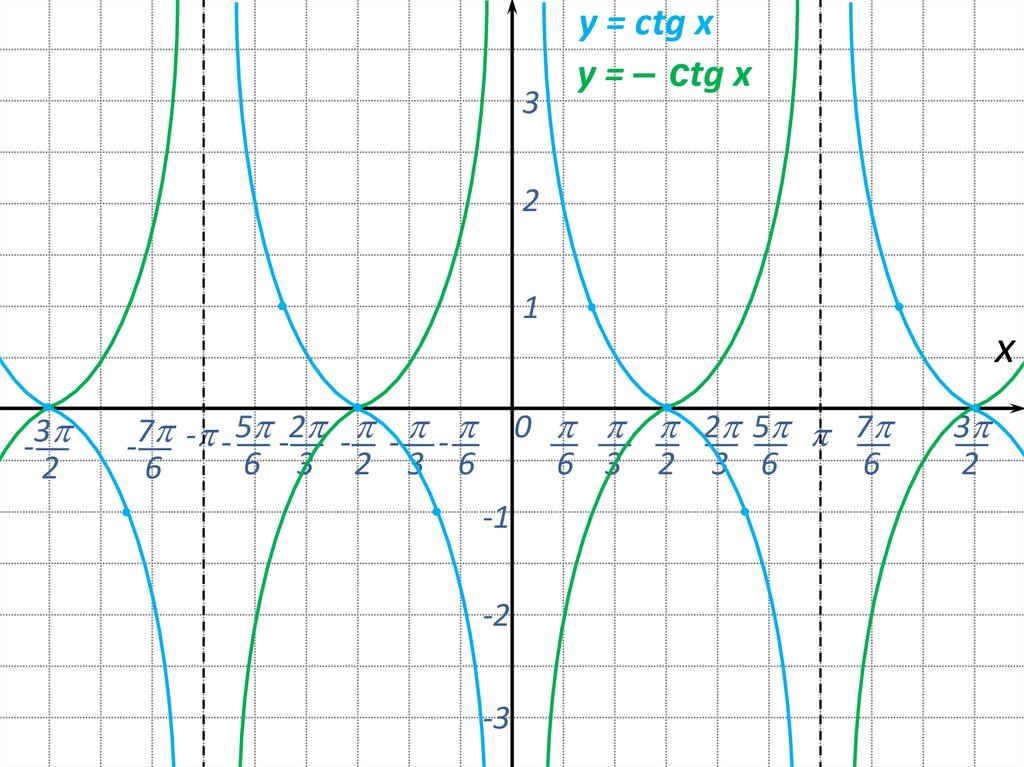
23.
3y = сtg x
y = – сtg x
2
1
х
-3
2
5 -2 - - -
7
6 3 2 3 6
6
0
6 3
-1
-2
-3
2 5 7
2
3 6
6
3
2
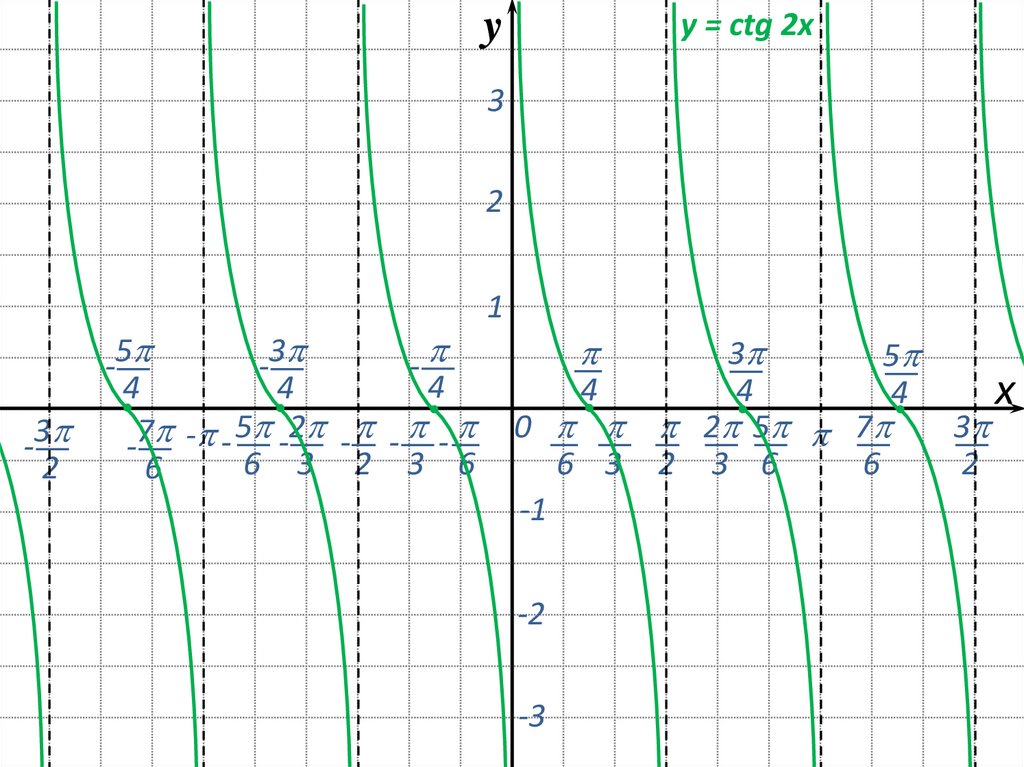
24.
yy = сtg 2x
3
2
-
-5
-3
4
4
4
5 -2 - - -
3
7
6 3 2 3 6
2
6
1
4
0
6 3
-1
-2
-3
3
5
4
4
2 5 7
2 3 6
6
3
2
х
25. Преобразование вида y = |f(x)|
— Это отображение нижней части графика функции y= f(x) в верхнюю полуплоскость относительно оси
абсцисс
с сохранением верхней
части графика
у
y = |f(x)|
y = f(x)
х
0
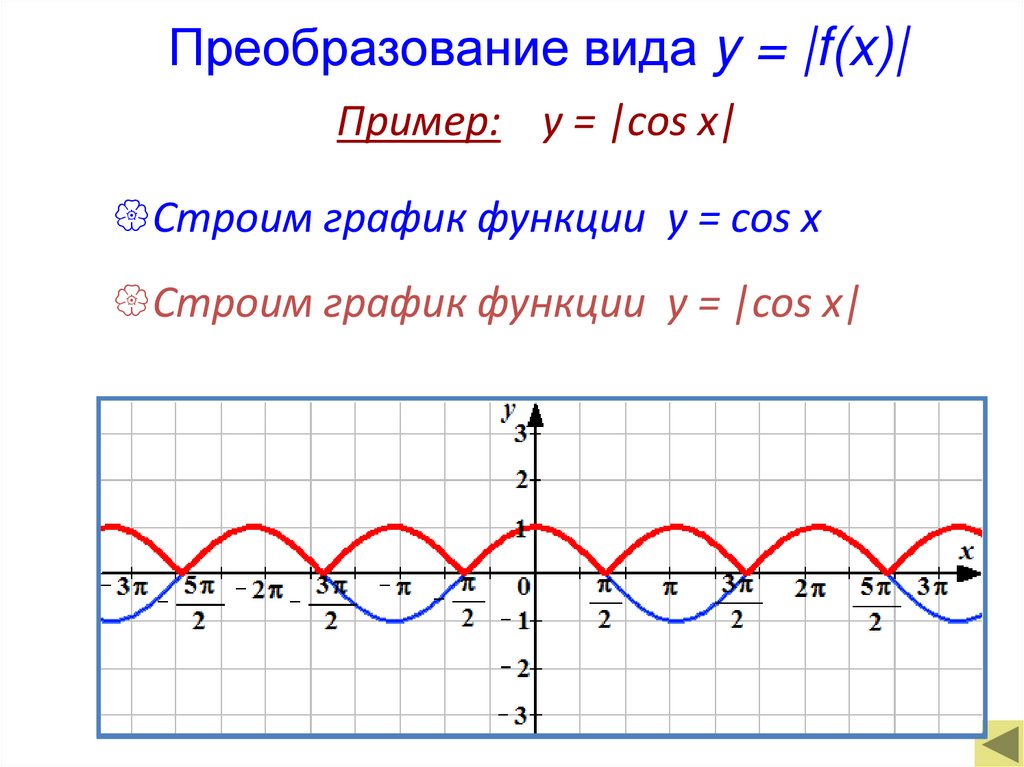
26. Преобразование вида y = |f(x)|
Пример: y = |cos x|Строим график функции у = cos x
Строим график функции у = |cos x|
27. Преобразование вида y = f (|x|)
— Это отображение правой части графика функцииy = f(x) в левую полуплоскость
относительно оси ординат
с сохранением правой части графика
у
y = f(|x|)
х
0
y = f(x)
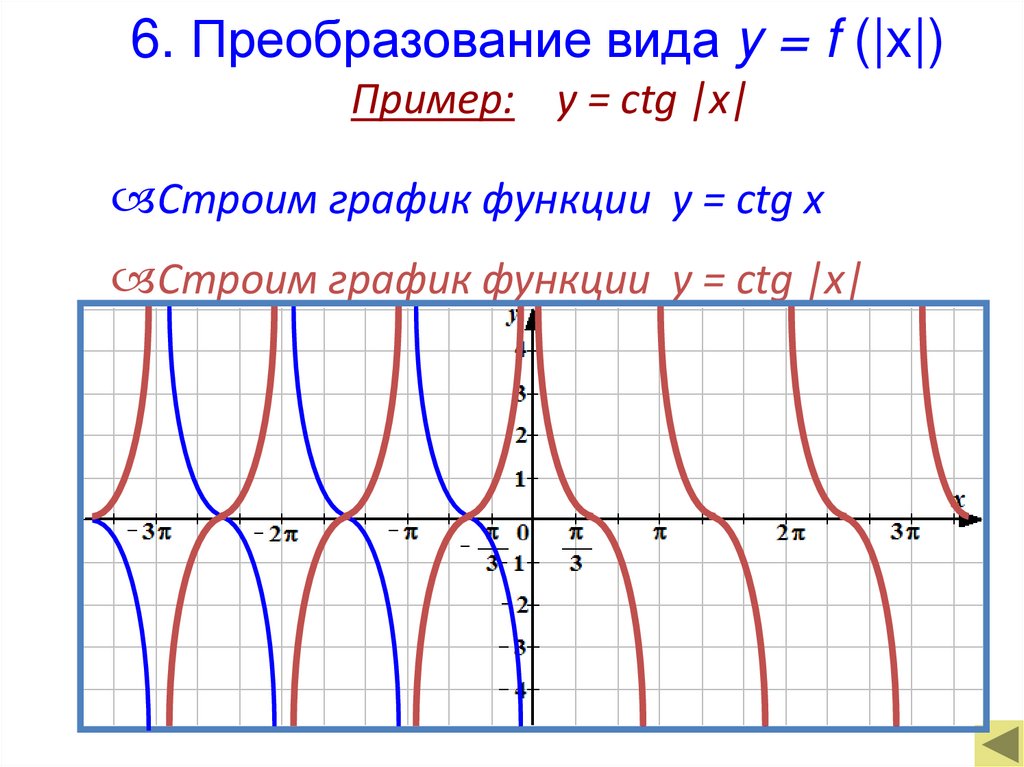
28. 6. Преобразование вида y = f (|x|)
Пример: y = ctg |x|Строим график функции у = ctg x
Строим график функции у = ctg |x|





 mathematics
mathematics








