тема 5 операторы и стац. задачи

1.

х
МОДУЛЬ 3. Тема 5. СТАЦИОНАРНЫЕ ЗАДАЧИ
КВАНТОВОЙ МЕХАНИКИ
5.1. Стационарные состояния
Волновая функция
5.2. Операторы физических величин
5.3. Частица в одномерной прямоугольной
яме с бесконечными внешними «стенками»
5.4.* Прохождение частиц сквозь
потенциальный барьер. Туннельный эффект
5.5.* Гармонический осциллятор

2. 5.1. Стационарные состояния

Волновая функция стационарного состояния частицы
имеет вид
( x, y, z ) e
1
iEt
функция ( x, y , z )
, где
является решением стационарного уравнения Шредингера
Ĥ E
ИЛИ
2
2m
2
( E U ) 0
где
2 потенциальная энергия
U ( x, y , z )
4 плотность вероятности
W
явно не зависит
от времени,
3 полная энергия в каком-либо квантовом состоянии
имеет определенное значение,
2
и вероятность
обнаружения частицы в какой-либо области пространства
не зависит от времени.

3.

Свойства волновой функции
Уравнение Шредингера – линейное дифференциальное уравнение, для которого
выполняется принцип суперпозиции: Если 1 и
2 решения
уравнения, то функция c1 1 c2 2 с произвольными постоянными
коэффициентами c1 и c2 тоже является решением этого же волнового
уравнения.
Принцип суперпозиции, необходимый для объяснения волновых свойств
частиц, и вероятностный смысл волновых функций определяют их свойства.
1. Из понятия плотности вероятности следует условие
нормировки: Если известно, что частица находится в объеме V
2
(достоверное событие), то
2
dV 1
V
2.
dV
V
функция должна быть конечной и однозначной. Только при
этом её физическая интерпретация как амплитуда вероятности имеет
смысл.

4.

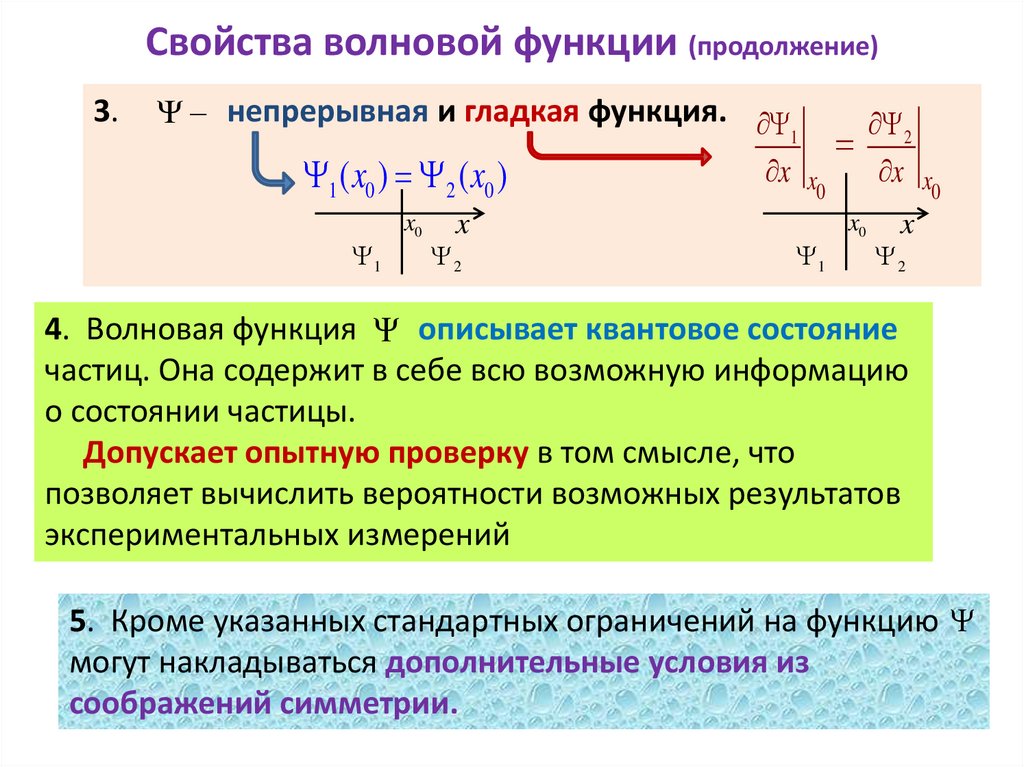
Свойства волновой функции (продолжение)
3.
непрерывная и гладкая функция.
2
1
x x
x x
1 ( x0 ) 2 ( x0 )
0
1
x0
x
2
1
0
x0
x
2
4. Волновая функция описывает квантовое состояние
частиц. Она содержит в себе всю возможную информацию
о состоянии частицы.
Допускает опытную проверку в том смысле, что
позволяет вычислить вероятности возможных результатов
экспериментальных измерений
5. Кроме указанных стандартных ограничений на функцию
могут накладываться дополнительные условия из
соображений симметрии.

5.

5.2. Операторы физических величин
Идея Макса Борна «о сопоставлении
физической величине определённого
оператора»:
Каждой физической величине f
соответствует определённый
оператор Ф̂ .
При этом соотношения между
операторами имеют ту же структуру, что и
соотношения между соответствующими
им физическими величинами в
классической механике.

6.

Оператор – это математическое правило, следуя
которому можно преобразовать одну функцию в
другую.
Такое преобразование может быть простым умножением
исходной функции на число или известную функцию,
дифференцированием функции, перестановкой аргументов
функции и др. Оператор обозначают буквой со «шляпкой» и
он действует на написанную за ним функцию: L̂
Пример: Функцию
функцию cos x
sin x можно преобразовать в
с помощью оператора
d
ˆ
дифференцирования L
:
dx
d
cos x sin x
dx

7.

Если при действии оператора Ф̂
на
некоторую функцию получается та же
самая функция, умноженная на число f :
Ф̂ f
,
то такую функцию называют собственной
функцией оператора Ф̂ , а число f – его
собственным значением.

8.

Оператор импульса
Уравнение Шредингера для свободной частицы
(потенциальная энергия U=0 ), когда частица
движется в одном направлении (ось X) с импульсом
px p имеет вид
2
2
2m x
2
i
t
Решением этого уравнения является плоская волна де Бройля, которая
описывает квантовое состояние свободно движущейся частицы:
A e
i
( Et px )
E p 2 2m
,
где
p
i x ,
Дифференцируя выражение для плоской волны по x, получим
i
p
x
x
, или в операторном виде
pˆ x p .
Оператор компоненты импульса равен:
pˆ x i
x

9.

Операторы полной энергии , кинетической и
потенциальной энергии.
Путем дифференцирования плоской волны де Бройля по
времени t можно найти оператор полной энергии E:
Ê i
t
Дважды дифференцируя выражение для плоской волны де Бройля по координате x ,
получим:
2
2
px 2 ,
2
x
или в операторном виде:
Оператор квадрата импульса равен
pˆ x 2 px 2
2
pˆ x 2 pˆ x pˆ x 2 2
x
Умножая оператор квадрата импульса на 1 2m ,
Получим
оператор кинетической энергии E K :
2
2
2
ˆ
р
Eˆ K
2m
2m x 2
Оператор потенциальной энергии – это оператор умножения: Uˆ U ( x)

10. Обобщение на трехмерный случай

x
Обобщение на трехмерный случай
z
y
Обобщение на трехмерный случай сводится к введению
векторного оператора импульса:
ˆ
P ex pˆ x ey pˆ y ez pˆ z i (ex
ey
ez ) i
x
y
z
Оператор кинетической энергии:
2
2
2
ˆˆ
ˆ
p
pp
Eˆ K
2
2m 2m
2m
2m
Оператор потенциальной энергии:
Uˆ U ( x, y, z )
Оператор Гамильтона Ĥ для полной энергии:
Hˆ Eˆ K Uˆ
2
2m
2 U ( x, y, z ) (гамильтониан)
Стационарное уравнение Шредингера в операторном виде:
Eˆ K Uˆ E ,
2
2m
2 U ( x, y, z ) E , или
( x, y , z )
Ĥ E

11. Частица в одномерной потенциальной яме с непроницаемыми стенками

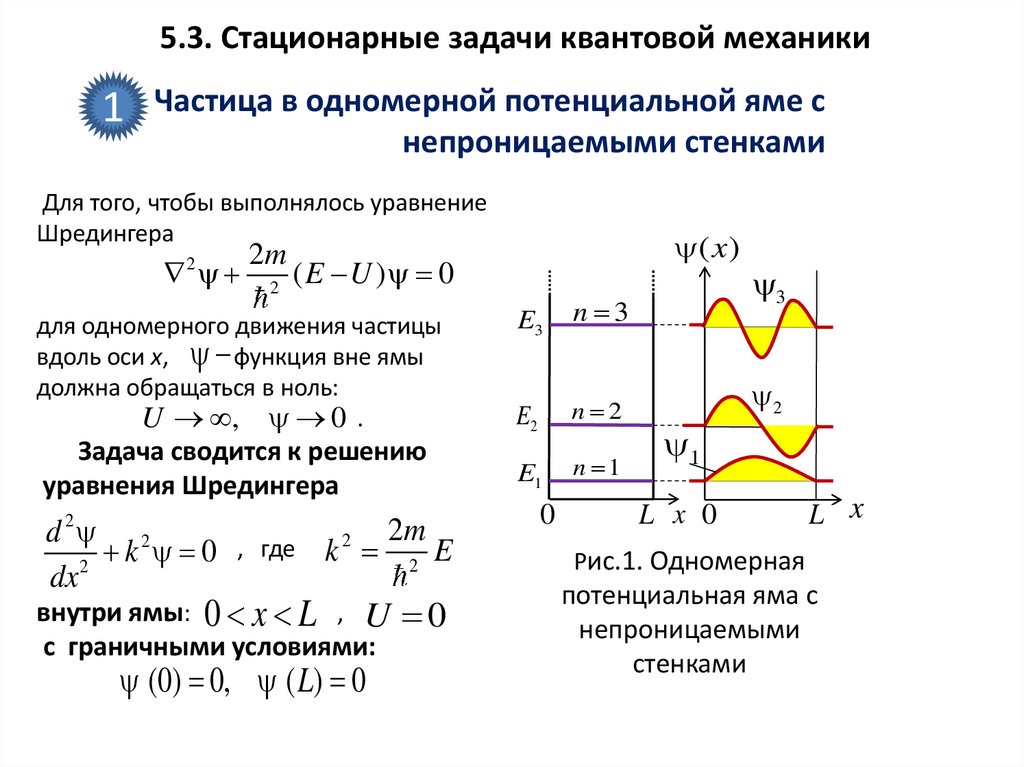
5.3. Стационарные задачи квантовой механики
1 Частица в одномерной потенциальной яме с
непроницаемыми стенками
Для того, чтобы выполнялось уравнение
Шредингера
2
2m
2
( x)
( E U ) 0
для одномерного движения частицы
вдоль оси x, функция вне ямы
должна обращаться в ноль:
U , 0 .
Задача сводится к решению
уравнения Шредингера
d 2
, где k 2
k
0
dx 2
2
2m
E3
n 3
E2
n 2
E1
n 1
0
3
2
1
L x 0
L x
E
Рис.1. Одномерная
внутри ямы: 0 x L , U 0
с граничными условиями:
потенциальная яма с
непроницаемыми
стенками
(0) 0, ( L) 0
2

12.

d 2
2
Решение уравнения
k
0 хорошо известно из теории колебаний.
2
dx
Запишем это решение в виде ( x) A sin(kx )
Из граничного условия (0) 0 при
x 0 следует, что 0
.
Другое граничное условие ( L) 0 приводит к квантованию энергии:
x L, ( L) 0,
k
2m
2
E
sin kL 0,
kn L n , n 1, 2,3,
2 2 2
En
n ,
2
2mL
n 1, 2,3,
kn L n ,
где n – квантовое число, а соответствующее ему значение En называется
уровнем энергии.
Первые три уровня энергии изображены . Состояние частицы
с наименьшей энергией E1 2 2 2mL2 , ( n 1 ) называется основным
(невозбужденным) состоянием,
все остальные состояния являются возбужденными.

13.

( x)
Волновые функции частицы:
n
x
L
Множитель A находим из условия
нормировки
2
n ( x) A sin kn x A sin
n
E3
dx 1,
L
A2 sin 2 (
0
n
L
x) dx A2 1 , A
L
2
2
L
n 3
E2
n 2
E1
n 1
0
2 ( x)
3
32
2
22
1
L x0
12
L
0
L x
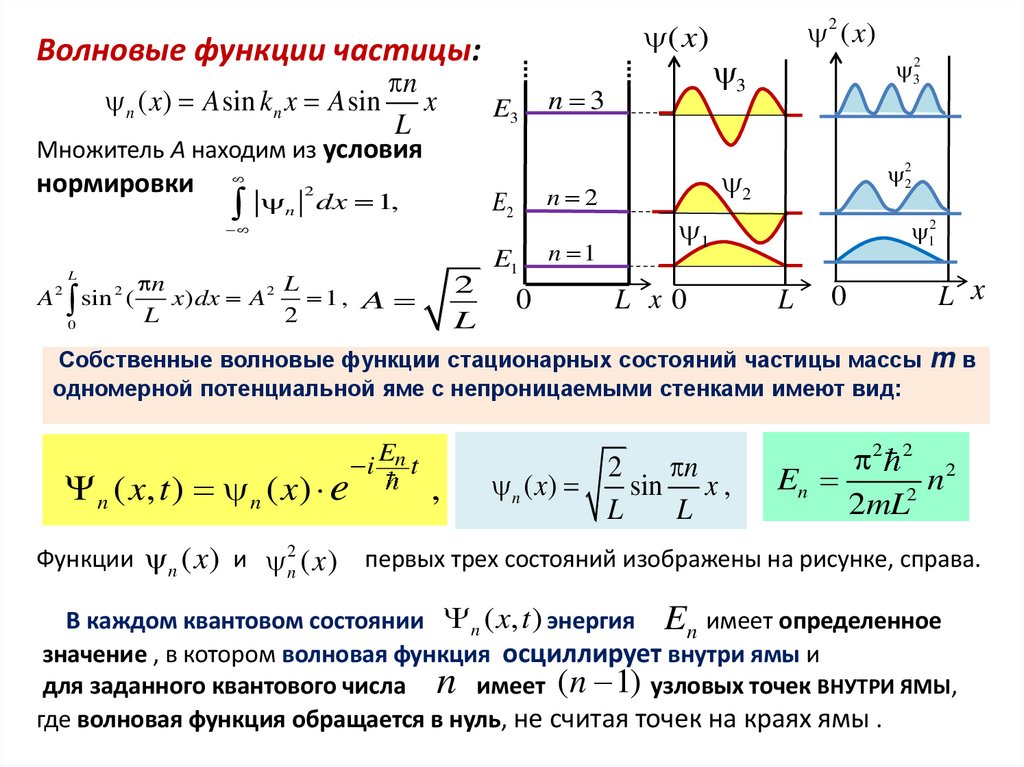
Собственные волновые функции стационарных состояний частицы массы m в
одномерной потенциальной яме с непроницаемыми стенками имеют вид:
n ( x, t ) n ( x ) e
Функции n ( x ) и 2n ( x )
i
En
t
,
2
n
n ( x)
sin x ,
L
L
2 2 2
En
n
2
2mL
первых трех состояний изображены на рисунке, справа.
В каждом квантовом состоянии n ( x, t ) энергия En имеет определенное
значение , в котором волновая функция осциллирует внутри ямы и
для заданного квантового числа n имеет ( n 1) узловых точек ВНУТРИ ЯМЫ,
где волновая функция обращается в нуль, не считая точек на краях ямы .

14.

О вероятности обнаружения частицы в потенциальной яме.
Плотность вероятности: ( x) n 2n ( x)
2
Условие нормировки:
2 2 n
sin
x
L
L
2
n
1
2 n
W ( x)dx sin 2 ( x) dx 1 cos(
x) dx 1
L
L
L
L
0
0
0
L
L
L
2
n
означает, что суммарная площадь под кривой зависимости n ( x ) от x на графике
равна единице (для достоверного события - «частица находится где-то в яме»
- вероятность W 1 ).
2
1 Вероятность W12 обнаружить частицу внутри ямы
в основном состоянии с квантовым числом n 1
в интервале от x1 до x2 равна
12 ( x )
W12
x2
W12 12 ( x)dx
x1
,
x1
0 W12 1
0
W
x2
L
x

15.

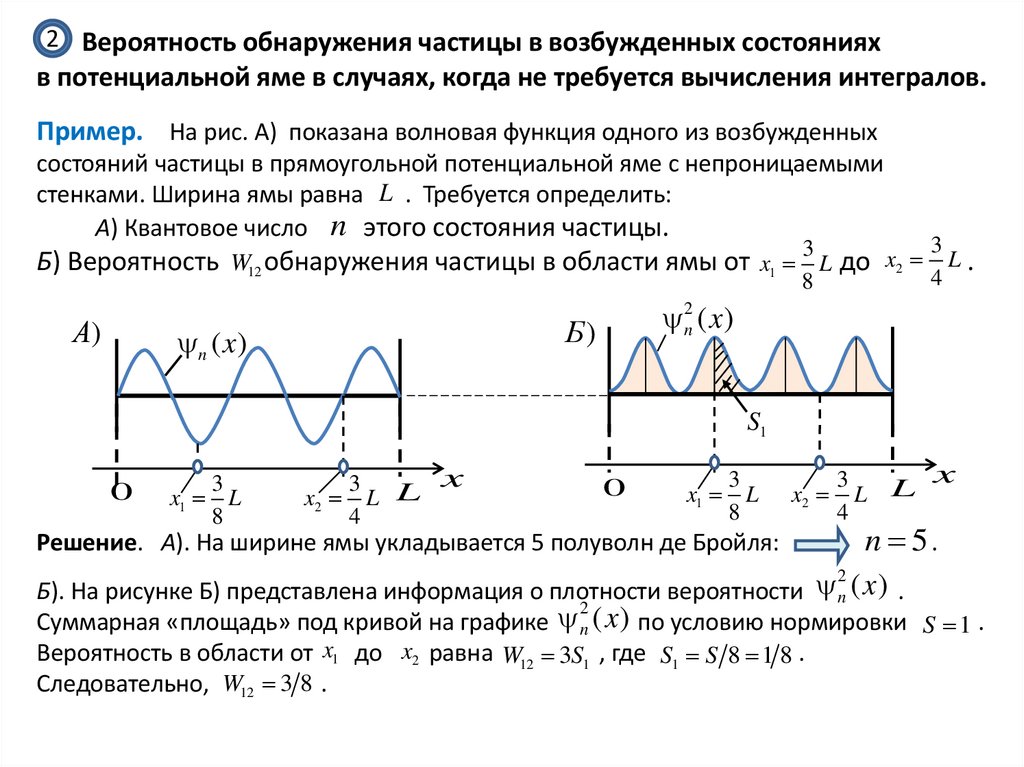
2 Вероятность обнаружения частицы в возбужденных состояниях
в потенциальной яме в случаях, когда не требуется вычисления интегралов.
Пример. На рис. А) показана волновая функция одного из возбужденных
состояний частицы в прямоугольной потенциальной яме с непроницаемыми
стенками. Ширина ямы равна L . Требуется определить:
А) Квантовое число n этого состояния частицы.
3
3
8
Б) Вероятность W12 обнаружения частицы в области ямы от x1 L до x2 L .
4
А)
2n ( x )
Б)
n ( x)
S1
0
3
x1 L
8
x
3
x2 L L
4
0
3
x1 L
8
3
x2 L
4
L
x
n 5.
Решение. А). На ширине ямы укладывается 5 полуволн де Бройля:
Б). На рисунке Б) представлена информация о плотности вероятности n ( x ) .
2
Суммарная «площадь» под кривой на графике n ( x ) по условию нормировки S 1 .
Вероятность в области от x1 до x2 равна W12 3S1 , где S1 S 8 1 8 .
Следовательно, W12 3 8 .
2

16. Движение частицы в области прямоугольной потенциальной ступеньки.

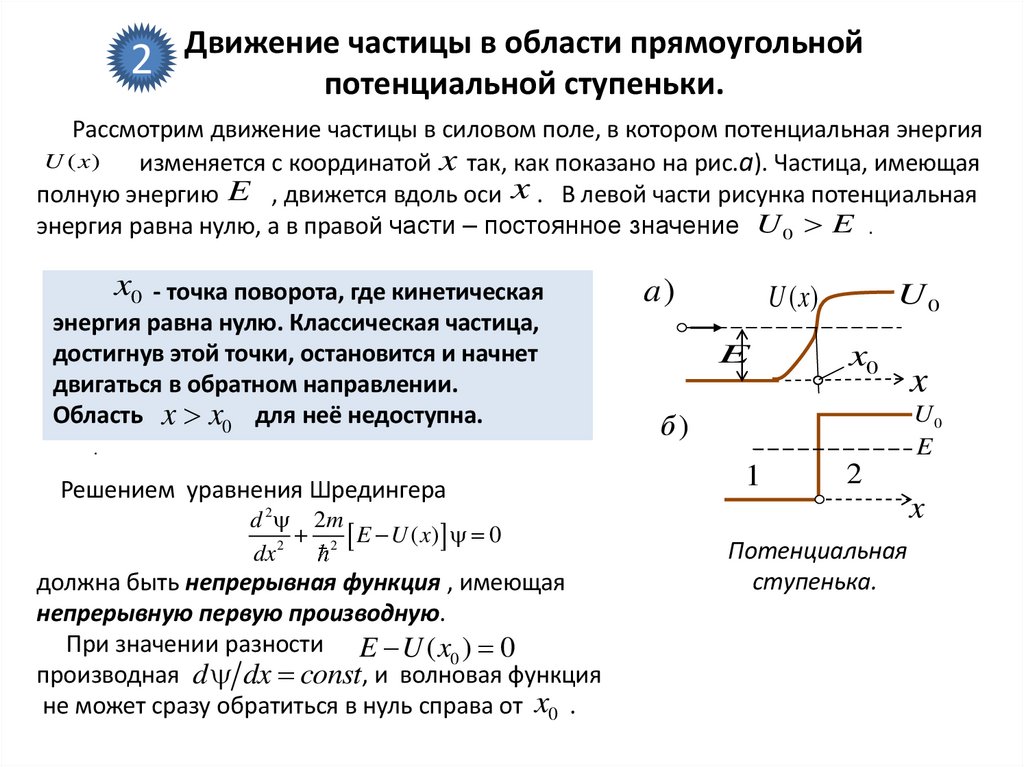
2
Движение частицы в области прямоугольной
потенциальной ступеньки.
Рассмотрим движение частицы в силовом поле, в котором потенциальная энергия
U ( x)
изменяется с координатой x так, как показано на рис.а). Частица, имеющая
полную энергию E , движется вдоль оси x . В левой части рисунка потенциальная
энергия равна нулю, а в правой части – постоянное значение U 0 E .
x0 - точка поворота, где кинетическая
энергия равна нулю. Классическая частица,
достигнув этой точки, остановится и начнет
двигаться в обратном направлении.
Область x x0 для неё недоступна.
a)
U0
U ( x)
E
x0
U0
E
б)
.
Решением уравнения Шредингера
d 2 2m
2 E U ( x) 0
dx 2
должна быть непрерывная функция , имеющая
непрерывную первую производную.
При значении разности E U ( x0 ) 0
производная d dx const, и волновая функция
не может сразу обратиться в нуль справа от x0 .
x
1
2
x
Потенциальная
ступенька.

17.

В соответствии с вероятностным смыслом волновой функции
это означает отличную от нуля вероятность обнаружить частицу
в области x x0 .
Квантовая частица способна проникать в область,
запрещенную классической механикой.
Чтобы упростить ситуацию, заменим непрерывную функцию U ( x) ,
изображенную на рис. а), ступенчатой функцией, показанной на рис. б),
а начало координат поместим в точку поворота, так что x0 0 .
Будем искать решение уравнения Шредингера в областях 1 и 2.
В области 1, ( x 0 ), уравнение Шредингера принимает вид
k12 0, где
k12 2mE ,2
1
два штриха над волновой функцией означают двойную производную по
координате . Общее решение этого уравнения
ik1x
ik1x
1 ( Ae
Be
) e
представляет сумму двух волн, падающую с амплитудой А и
отраженную от потенциальной ступеньки волну с амплитудой В.
i E t
U0
E
2
x

18.

В области 2, ( x 0 ), уравнение Шредингера k22 0 ,
где
k22 2m(U 0 E )
2
,
имеет общее решение
2 Ce k2 x De k2 x
U0
E
2
1
x
0
2 должна быть ограниченной, а второе слагаемое в решении
Поскольку
неограниченно возрастает с увеличением x , то необходимо, чтобы D 0 .
Таким образом физически приемлемым решением является
2 Ce k2 x
На границе раздела областей 1 и 2, то есть при x = 0, должны выполняться
условия непрерывности пси-функций и их производных:
1 (0) 2 (0)
1 (0) 2 (0)
A B C
ik1 A ik1B k2C
(5)

19.

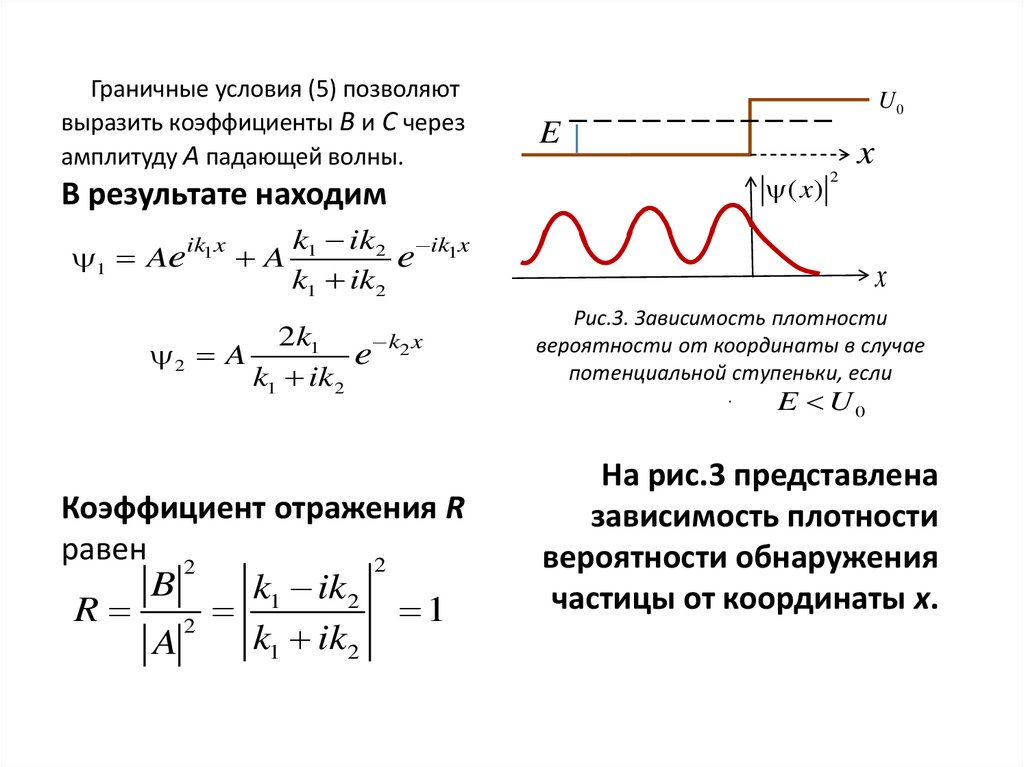
Граничные условия (5) позволяют
выразить коэффициенты В и С через
амплитуду А падающей волны.
U0
E
x
( x)
В результате находим
ik1x
1 Ae
2
k1 ik2 ik1x
A
e
k1 ik2
2k1
2 A
e k2 x
k1 ik 2
Коэффициент отражения R
равен 2
2
B
k1 ik2
R 2
1
k1 ik2
A
x
Рис.3. Зависимость плотности
вероятности от координаты в случае
потенциальной ступеньки, если
.
E U0
На рис.3 представлена
зависимость плотности
вероятности обнаружения
частицы от координаты x.

20.

Коэффициент отражения определяет вероятность того, что частица
отразится от ступеньки.
R 1 означает: в установившемся (стационарном) состоянии
вся энергия падающей волны отражается, однако в классически
запрещенной области существует определенная вероятность
обнаружить там частицу. И эта вероятность равна
W( x 0) 2
0
2
4k12
2k12
2 k2 x
2
2
dx A 2
e
dx A
2
k1 k2 0
k2 (k12 k22 )
На глубине
1
xэфф
2k2 2 2m(U 0 E )
плотность вероятности 2 уменьшается в e 2, 72 раза.
Величина xэфф называется эффективной глубиной
проникновения квантовой частицы в область, запрещенную
классической механикой.
2

21.

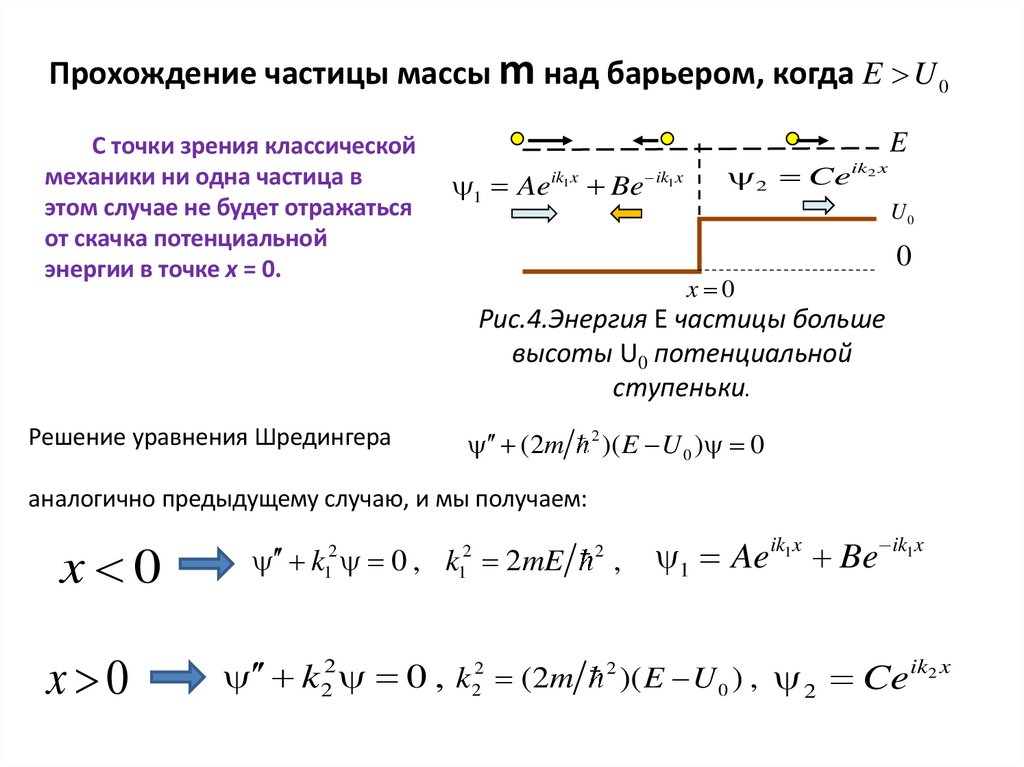
Прохождение частицы массы m над барьером, когда E U 0
С точки зрения классической
механики ни одна частица в
этом случае не будет отражаться
от скачка потенциальной
энергии в точке x = 0.
E
1 Ae
ik1 x
Be
ik1 x
2 Ceik2 x
U0
0
x 0
Рис.4.Энергия E частицы больше
высоты U0 потенциальной
ступеньки.
Решение уравнения Шредингера
(2m
2
)( E U 0 ) 0
аналогично предыдущему случаю, и мы получаем:
x 0
x 0
k12 0 , k12 2mE
k22 0 , k22 (2m
2
ik1 x
ik1 x
Ae
Be
,
1
2
)( E U 0 ) , 2 Ceik2 x

22.

Из граничных условий о непрерывности функций и их производных при x 0
находятся амплитуды B и C:
k1 k2
2k1
B
k1 k2
C
A ,
k1 k2
A
По аналогии с плотностью потока частиц jN nv , где
скорость v частиц, n плотность частиц (число частиц в единице объема),
введем плотность потока вероятности
2
jW W v v ,
v скорость одной частицы.
где
Коэффициенты отражения R и прохождения D определяются как :
R
jотр
jпад
2
отр 1
пад 1
2
2
2
k1 k2
,
2
A
k1 k2
B
D
jпрош
jпад
2 2
2
пад 1
2
2
C k2
2
A k1
4k1k2
(k1 k2 )2
Здесь использовалось соотношение v p m k m . Можно убедиться,
что R D 1 .
Таким образом, существует отличная от нуля вероятность отражения, даже
если E U 0 . Этот эффект является чисто квантовым и объясняется
наличием у частицы волновых свойств.
Интересно отметить, что коэффициенты R и D не изменятся, если k1 и k2
поменять местами, что соответствует случаю, когда частица движется к
потенциальной ступеньке справа налево.

23.

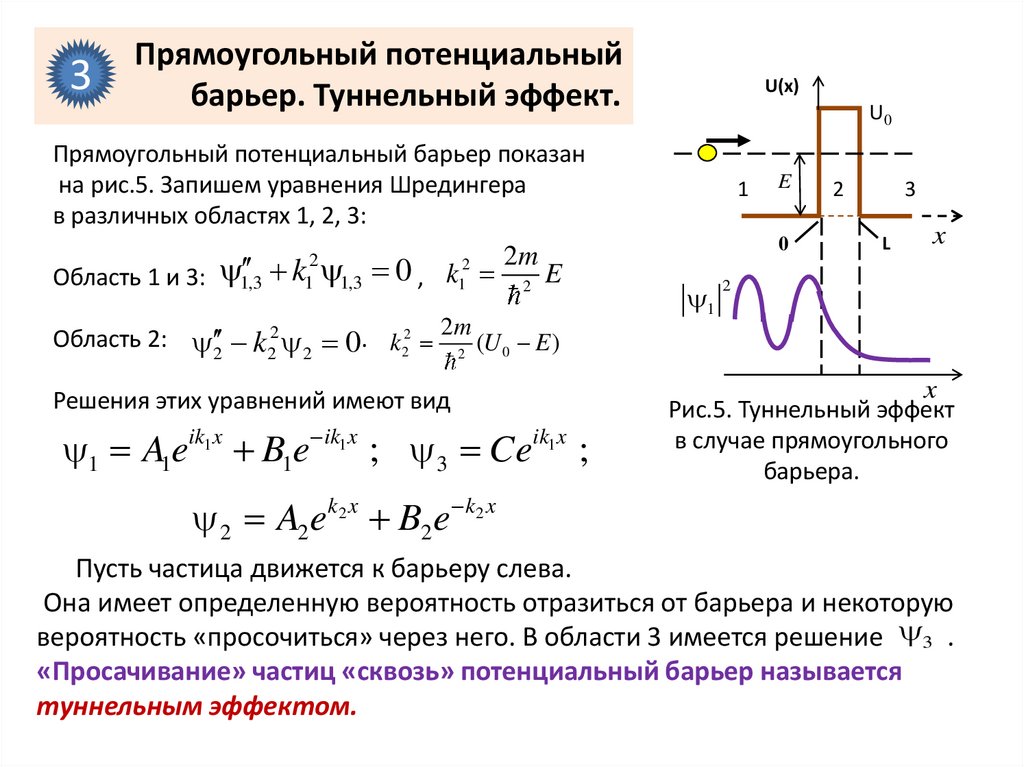
3
Прямоугольный потенциальный
барьер. Туннельный эффект.
U(x)
U0
Прямоугольный потенциальный барьер показан
на рис.5. Запишем уравнения Шредингера
в различных областях 1, 2, 3:
2m
2
2
k
0
k
E
Область 1 и 3: 1,3
, 1
1 1,3
2
Область 2: 2 k22 2 0. k22 2m
(U 0 E )
2
Решения этих уравнений имеют вид
1 A1eik1x B1e ik1x ; 3 Ceik1x ;
1
E
0
1
3
2
L
x
2
x
Рис.5. Туннельный эффект
в случае прямоугольного
барьера.
2 A2 e k2 x B2e k2 x
Пусть частица движется к барьеру слева.
Она имеет определенную вероятность отразиться от барьера и некоторую
вероятность «просочиться» через него. В области 3 имеется решение 3 .
«Просачивание» частиц «сквозь» потенциальный барьер называется
туннельным эффектом.

24.

Вероятность проникновения частицы в область 3
определяется коэффициентом прозрачности барьера
D C
2
A1
2
В том случае, когда k2 L 1 (для электрона это условие выполняется уже
при ширине барьера в несколько атомных слоев), коэффициент прозрачности
равен
D
16k12 k22
2 k2 L
e
(k12 k22 )
или
E E
2L
D 16 1 exp
2m(U 0 E )
U0 U0
Основной вклад в зависимость D от параметров задач
дает экспонента. Множитель перед экспонентой является
медленно изменяющейся функцией отношения E U 0 ,
численное значение которой сравнимо с единицей.
Поэтому часто при оценке коэффициента прозрачности
используется выражение
2L
D exp
2m(U 0 E )

25. Частица в прямоугольной потенциальной яме конечной глубины.

4
Частица в прямоугольной
потенциальной яме конечной глубины.
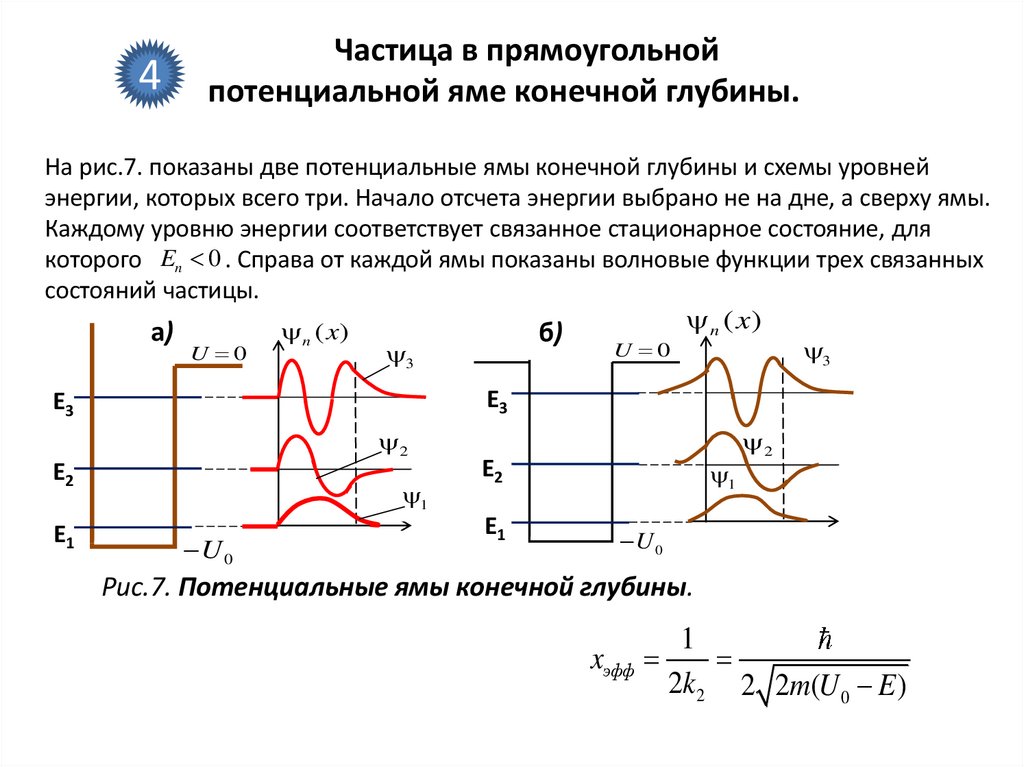
На рис.7. показаны две потенциальные ямы конечной глубины и схемы уровней
энергии, которых всего три. Начало отсчета энергии выбрано не на дне, а сверху ямы.
Каждому уровню энергии соответствует связанное стационарное состояние, для
которого En 0 . Справа от каждой ямы показаны волновые функции трех связанных
состояний частицы.
n ( x)
n ( x)
а)
б)
U 0
3
U 0
3
E3
E3
2
E2
E1
1
U 0
E2
E1
1
2
U 0
Рис.7. Потенциальные ямы конечной глубины.
1
xэфф
2k2 2 2m(U 0 E )

26.

В яме на рис.7,а потенциальная энергия на левой стенке стремится к
бесконечности, поэтому волновые функции на этой стенке обращаются в нуль. Вне
ямы (слева) 0 . Волновая функция остается непрерывной, но перестает быть
гладкой. Разрыв первой производной функции на левой стенке ямы обусловлен
предельным переходом U , что не реализуется в конкретных физических
ситуациях.
На правой стенке для частицы в состояниях с энергиями En имеется
потенциальный барьер конечной высоты, и частица с некоторой вероятностью
проникает в классически запрещенную область под барьером. Это обусловлено тем,
что волновая функция должна быть непрерывной и гладкой, она не может
«оборваться» на правой стенке и должна продолжаться под барьер. Глубина xэфф
проникновения под барьер увеличивается с уменьшением массы
разности (U0 En ) .
m частицы и
Аналогично объясняется и вид волновых функций в случае ямы на рис.7, б. Заметим,
что функция 1 имеет один экстремум и ни одного нуля, функция 2 имеет два
экстремума и один нуль внутри ямы, следующая функция – три экстремума и два нуля,
и т.д.
В потенциальной яме с двумя бесконечно высокими (непроницаемыми) стенками
число состояний частицы (число уровней энергии) бесконечно велико. В яме конечной
глубины число уровней энергии в яме ограничено и зависит от ширины ямы L и
глубины U0.

27. Когда в яме существует только одно стационарное состояние?

5
Когда в яме существует только одно
стационарное состояние?
Выясним, когда в яме может существовать
только одно связанное состояние (рис.8), и оно
является основным. Для этого воспользуемся
соотношением неопределенностей
p x
Полагая, что x L , где L ширина ямы,
неопределенность в импульсе p p ,
для кинетической энергии частицы в яме
2
2
2mL2 .
получим EK p 2m
0
E1
U 0
EK
Рис.8. Потенциальная яма с
одним уровнем энергии.
Чтобы частица могла локализоваться внутри ямы, необходимо выполнение
2
неравенства
EK U 0 , или
2
U0L
2m
Полученное условие является приближенным. Строгое решение задачи о
потенциальной яме на рис.7,б с использованием уравнения Шредингера приводит к
неравенству U 0 L2 2 2 2m
Если потенциальная яма слишком узкая или слишком мелкая, в ней отсутствуют
связанные состояния. С увеличением произведения U 0 L2 появляется сначала один
уровень энергии, затем второй, третий и так далее.

28. Выводы:

6
Выводы:
1. Энергия частицы E в потенциальной яме не может принимать
произвольных значений, она принимает ряд дискретных
значений, если выполнено условие U 0 L2 2 2 2m . Квантовая
частица не может упасть на дно ямы. Наименьшее значение
называется энергией нулевых колебаний.
2. Для одномерного движения волновая функция n 1
обращается в нуль внутри ямы n раз.
3. Если стенки ямы глубиной U 0 имеют конечную
толщину, то частица может покинуть яму в результате
туннельного эффекта.

29. Квантовый гармонический осциллятор.

7 Квантовый гармонический осциллятор.
Гармонический осциллятор – это система, способная совершать
гармонические колебания.
Малые колебания вблизи положения
равновесия можно считать гармоническими.
Примером таких колебаний в квантовой механике являются колебания
атомов в молекулах, твердых телах и т.д.
Гармонические колебания частицы под действием
возвращающей квазиупругой силы F x
в классической физике описывается уравнением
2
, или x 2 x 0 , где m0 .
m0 x x
Здесь частота гармонических колебаний, m0- масса
частицы.
Потенциальная энергия такого осциллятора равна
x 2 m0 2 2
U ( x)
x
2
2

30.

Квантово-механическая задача о гармоническом осцилляторе
сводится к задаче о движении частицы в параболической потенциальной
яме и решению стационарного уравнения Шредингера
m0 2 x 2
U ( x)
2
x
2m0
m0 2 x 2
2 E
0
2
Решение этой задачи приводит к квантованию энергии в
виде
n 0,1, 2,3,
E (n 1 2)
n
Число n называется колебательным квантовым числом.

31.

Не приводя математического решения задачи, рассмотрим вид волновых
функций из общих соображений. Пусть частица обладает полной энергией En .
Точки a0 и a0 , в которых полная энергия En U ( x) m0 2 x 2 2 , являются
для частицы классическими точками поворота. Подставляя в это равенство x a0 ,
получим, что
a0 2En m0 2
В основном состоянии с минимальной энергией E0 2 , n 0 (как и в
основном состоянии в прямоугольной потенциальной яме с шириной 2a0 )
волновая функция 0 ( x ) имеет экстремум в центре ямы ( x 0) и нигде не
обращается в нуль. Эта функция простирается за пределы точек поворота
так, что обеспечивается непрерывность самой функции и её
a0 2 E0 m0 2
первой производной при x a0 . Непосредственной подстановкой в
уравнение Шредингера можно убедиться, что функция
0 ( x)
1
x0
где x0
Если
x2
exp 2
2 x0
m0 , является его решением для E E0
x , то 0 ( x) 0 .
2 .

32.

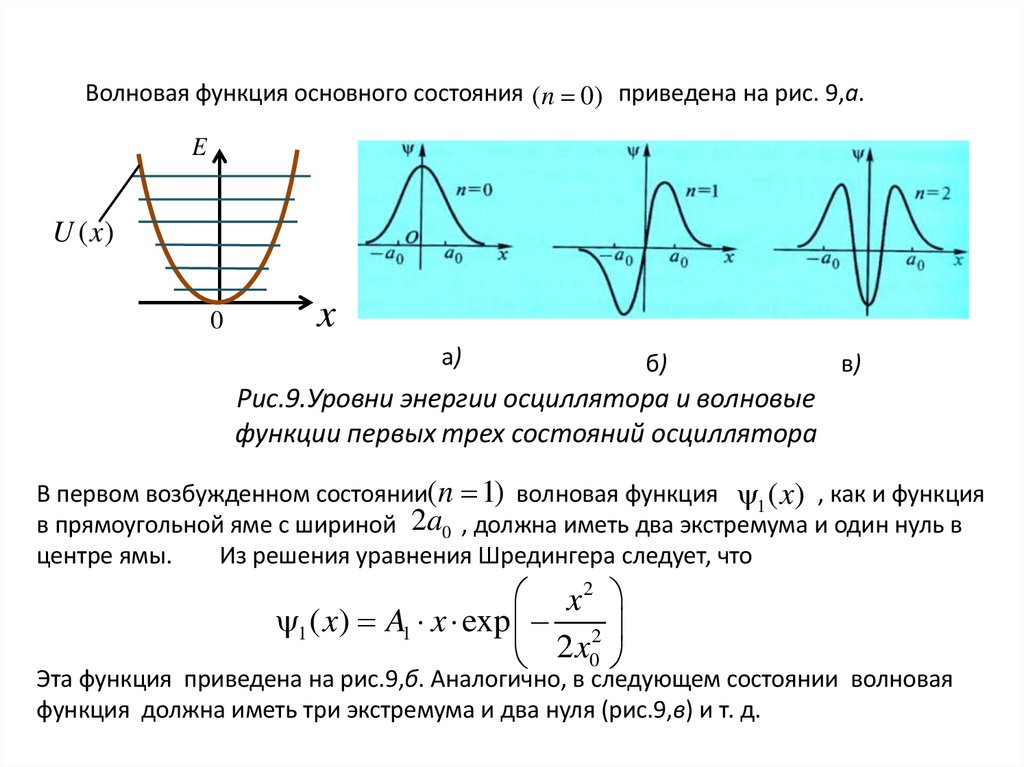
Волновая функция основного состояния (n 0) приведена на рис. 9,а.
E
U ( x)
0
x
а)
б)
в)
Рис.9.Уровни энергии осциллятора и волновые
функции первых трех состояний осциллятора
В первом возбужденном состоянии(n 1) волновая функция 1 ( x) , как и функция
в прямоугольной яме с шириной 2a0 , должна иметь два экстремума и один нуль в
центре ямы.
Из решения уравнения Шредингера следует, что
x2
1 ( x) A1 x exp 2
2 x0
Эта функция приведена на рис.9,б. Аналогично, в следующем состоянии волновая
функция должна иметь три экстремума и два нуля (рис.9,в) и т. д.

33.

Из приведенного рассмотрения следует:
1.
Квантовая механика не интересуется устройством осциллятора.
Общие принципы должны быть применимы для всех частиц
с массой m0 и всех возможных осцилляторов.
Можно ввести обобщенную координату q отклонения осциллятора
из положения равновесия и
обобщенный импульс p m0 q .
p 2 m0 2 q 2
Тогда энергия осциллятора запишется в виде E
2m0
2
2. Энергия осциллятора изменяется не непрерывно, а порциями
величины . Тем самым подтверждена гипотеза М.Планка,
с которой началось зарождение квантовой физики.

34.

3.
Когда энергия минимальна, классический осциллятор находится в
покое в положении равновесия.
Квантовый осциллятор в состоянии с минимальной энергией
при n 0 совершает колебания – «нулевые колебания». Среднее
значение координаты q 0 и импульса p 0 , а среднее значение
квадрата координаты q 2 0 и квадрата импульса p 2 0 .
Энергия колебаний равна 2 . Кинетическая и потенциальная
энергии не могут одновременно равняться нулю, это противоречило
бы соотношениям неопределенностей.
4. Представим себе, что между параллельными металлическими
экранами, перпендикулярно им, образовалась электромагнитная стоячая
волна. В такой волне происходят колебания электрического и магнитного
поля – это тоже осциллятор. Обобщенной координатой можно считать
напряженность электрического поля в какой-либо точке.
В качестве импульса должна быть величина, пропорциональная скорости
изменения электрического поля. Такой величиной является магнитное
поле.
При выборе таких обобщенных величин энергия будет иметь
такой же вид записи, как у осциллятора. К стоячей волне – осциллятору
можно применить уже известные результаты квантования.

35.

8
Бегущие волны
Рассмотрим бегущую волну. В этом случае тоже происходят периодические
колебания, и энергия для каждого волнового вектора k имеет такой же
вид, как для осциллятора.
Энергия волны определяется соотношением En (n 1 2)
и изменяется порциями величины , но в отличие от стоячей волны
бегущая волна обладает импульсом . Поэтому, когда номер возбуждения
бегущей волны с волновым вектором k (k 2 )
увеличивается на единицу (n n 1 ) , это означает появление
частицы-фотона с энергией E и импульсом p c .
Каждому k соответствует свой осциллятор, который может
находиться в определенном состоянии возбуждения.

36. Нулевые колебания

9
Нулевые колебания
В основном состоянии, состоянии с минимальной энергией,
происходят нулевые колебания. Можно найти вероятность того или иного
значения электрического или магнитного поля. Средний квадрат
напряженности электрического и средний квадрат напряженности
магнитного полей имеют неравные нулю значения, даже если в
пространстве нет ни одной частицы и ни одного фотона
электромагнитного поля. Фотоны возникают как возбужденные
состояния этого поля.
Существуют нулевые колебания в вакууме всех возможных
физических полей в основном состоянии, колебания, состоящие в
появлении и исчезновении электрон-позитронных, нуклонантинуклонных и других пар. С этой точки зрения вакуум наполнен
такими не родившимися, образующимися и исчезающими частицами.
Они называются виртуальными частицами. Достаточно возбудить
вакуум, сталкивая, например, два нуклона, виртуальные частицы могут
превратиться в реальные – при столкновении рождаются новые частицы.