НИР_КГ_Бинарное_лямбда_исчисления_расширенной_кодировки_Черча

1.

Бинарное лямбда
исчисления
расширенной кодировки
Черча
Екатерина Голова

2.

История
Λ-исчисление - формальная система, описывающая вычисления с помощью
функций и их применения.
○
○
1928: Давид Гильберт формулирует Entscheidungsproblem — существует ли
общий алгоритм вывода истинности формулы?
1936: Алонзо Чёрч (λ-исчисление) и Алан Тьюринг (машина Тьюринга)
независимо показывают: такого алгоритма не существует.
Теорема Чёрча-Тьюринга:
Не существует алгоритма который бы принимал в качестве входных данных
описание любого другого алгоритма на который были 2 возможных ответа: ‘’да’’
или ‘’нет’’ используя при этом формальную мат. логику.

3.

История
Таким образом, λ-исчисление впервые привлекло внимание, но продолжало
оставаться в области математической логики ещё несколько десятилетий. Однако
в середине 1960-х годов Питер Ландин предложил новый взгляд на эту тему и
обратил внимание на то, что сложные языки программирования можно более
эффективно изучать, сформулировав их ядро в виде небольшой базовой системы,
описывающей основные механизмы языка, и дополнив её удобными
производными формами, которые можно было бы выразить через базовую
систему. В качестве такой основы, Ландин выбрал λ-исчисление Чёрча.

4.

Основы
Лямбда-анализ на поверхности представляет собой особую запись для
функций. Оно чрезвычайно лаконично, но, на первый взгляд, сложно.
Давайте рассмотрим функцию 3x:
○
f(x)
= 3x
○ function f(x) begin f := 3∗x end;
○ (lambda (x)
(∗3x))
○ λ
x
. 3x
Mат. язык
Pascal
Lisp
Лямбда запись

5.

Основы - Определение комбинатора
В общем, функции в лямбда анализе могут быть высшего порядка.
Функции высшего порядка — это такие функции которые оперируют не
над множествами чисел, матрицами и тп., а над функциями ( higher-order
functions анг.)
Оператор — математические операции, применяемые к функциям, если
результат это тоже функция. Хотя сейчас они чаще всего называются
функционалами высших типов.
Комбинатор — это такой оператор, который нельзя получить из других
операторов.

6.

Комбинаторы - SKI логика
Шейнфинкель выделил три главных таких комбинатора:
○ (I x) = λx.x = x (единичный комбинатор)
○ (K x y) = λxy.x = x (поглотитель)
○ (S x y z) = λx.z λy.z = (x z)(y z) (заменитель)
Теперь выведем и определим некоторые другие комбинаторы:
○ (F x y) = (S K x y) = K y (x y) = y
○ (N x) = (F K x)

7.

Комбинаторы - отход от λ выражений
Давайте преобразуем λ выражение через комбинаторы.
Пример:
○ λxy.yx
λxy.yx = λx.λy.yx = λx.S(λy.y)λy.x = λx.SI λy.x =λx.SIKx =
= S(λx.SI)(λx.Kx) = (SKSI)(Sλx.K)λx.x
= (SKSI)(SKKI)

8.

Комбинаторы - булева логика
Рассмотрим комбинаторы K, F, N поближе и увидим:
(K)N = K(F)(K) = F
(F)N = F(F)(K) = K
При данных условиях N ведет себя как логическое ‘’Не’’
(K)K(K) = K(K)(K) = K
(K)(K)F = K(K)(F) = K
(K)K(F) = K(K)(F) = K
(K)(F)F = K(F)(F) = F
(F)K(K) = F(K)(K) = K
(F)(K)F = F(K)(F) = F
(F)K(F) = F(K)(F) = F
(F)(F)F = F(F)(F) = F
K - комбинатор логического ‘’Или’’, F - комбинатор логического ‘’И’’
ЕСЛИ = λxyf. λf(xyf)

9.

Комбинаторы - числа как функции
Числа Чёрча - это представления натуральных чисел в кодировке Чёрча. функция высшего порядка,
представляющая натуральное число n, - это функция, которая отображает любую функцию f в её nкратную композицию. Проще говоря, "значение" числа эквивалентно количеству раз, инкапсулируя
свой аргумент.
f∗n(x) = f(f(f(...f(x)))) = f∗f∗f∗…∗f(x)
+
ℤ
Опр. через функции
Опр. через λ-функции
0
f(x) = x
λf.I
1
f(x) = f~(x)
λf~.Ix.Y
2
f(x) = f~(f~(x))
λf~.Ix.Y Y
…
…
…
n
f(x) = f∗~n(x)
λf~.Ix.Y∗n

10.

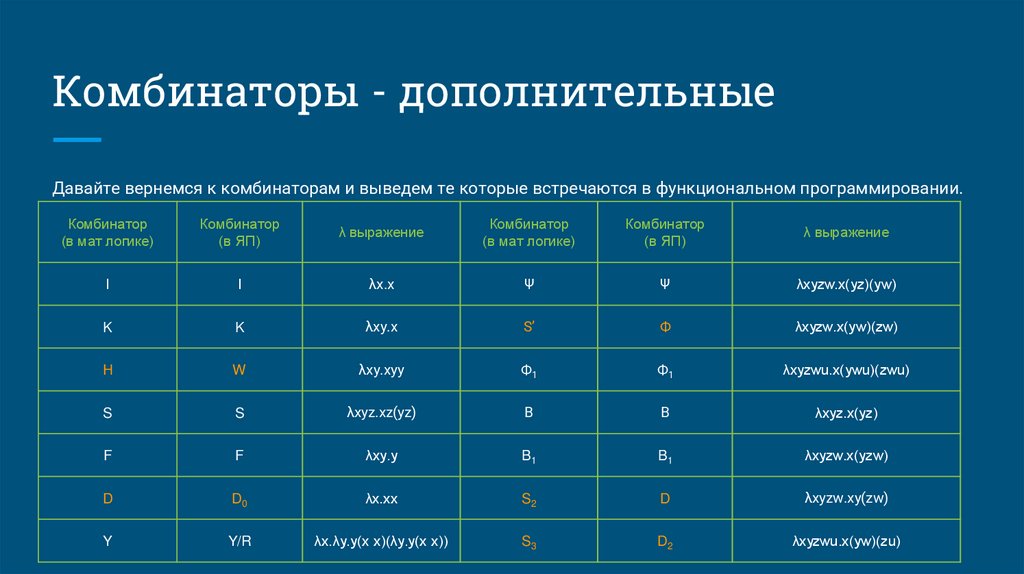
Комбинаторы - дополнительные
Давайте вернемся к комбинаторам и выведем те которые встречаются в функциональном программировании.
Комбинатор
(в мат логике)
Комбинатор
(в ЯП)
λ выражение
Комбинатор
(в мат логике)
Комбинатор
(в ЯП)
λ выражение
I
I
λx.x
Ψ
Ψ
λxyzw.x(yz)(yw)
K
K
λxy.x
S’
Ф
λxyzw.x(yw)(zw)
H
W
λxy.xyy
Ф1
Ф1
λxyzwu.x(ywu)(zwu)
S
S
λxyz.xz(yz)
B
B
λxyz.x(yz)
F
F
λxy.y
B1
B1
λxyzw.x(yzw)
D
D0
λx.xx
S2
D
λxyzw.xy(zw)
Y
Y/R
λx.λy.y(x x)(λy.y(x x))
S3
D2
λxyzwu.x(yw)(zu)

11.

Комбинаторы - числа Чёрча
Мы определили числа Чёрча через функции, теперь определим операции над ними:
succ(n) = n + 1, succ(n) = λn.λf.λx.f (n f x) = λ succ n.succ(n)
S+
f∗(n+1)(x) = f(f∗n(x))
plus(m, n) = K m n succ(m)
P+
f∗(m+n)(x) = f∗m(f∗n(x))
mult(m, n) = K m n add(m, n)
P*
f∗(m∗n)(x) = (f∗n)∗m(x)
prev(n) = n - 1, prev(n) = λn.λf.λx. (n I(n, λsucc(n, -1).λn.x))
minus(m, n) = K m n prev(m)
P-
S-

12.

Исследование - Расширение на Z
Поскольку λ-исчисление рассматривается как универсальная модель
вычислимых функций, в нем должно быть представимо стандартное
кольцо целых чисел Z со всеми базовыми арифметическими операциями.
Целое число представляем как пару [b, n], где b - булев (плюс или минус), а n
- натуральное число в кодировке Чёрча; далее вводим λ-термы для
конструктора пары, проекций и булева знака.
○ [a, b] = λ a b f.f a b, тогда
○ nZ = [b, nN]

13.

Исследование - Очевидное расширение на Z/dZ
Теперь перейдём от целых чисел Z к кольцу вычетов Z/dZ. Тут два есть способа. Достаточно
очевидный, но алгоритмически неэффективный. И через проекции. Сначала рассмотрим первый
способ.
Функция остатка от деления у нас уже построена, поэтому через примитивную рекурсию (индукцию по
аргументу) можно явно выписать лямбда-термы для операций в Z/dZ.
○
○
M≡ x d = [ x (λp. H( = (S+ p₂) d) ([S+ p₁, 0], [p₁, S+ p₂])) [0, 0] ]₂
M≡Z/dZ x = Ṡ xZ λt.[T, P- dZ (M≡ xZ)₂ d] λt.[T, 0Z] λt.[T, M≡ (xZ)₂ d]
Первый терм M≡ для натурального x и модуля d по шагам перебирает x, накапливая пару [частное,
остаток], и в конце возвращает остаток;
Второй терм M≡Z/dZ учитывает знак целого xZ: для положительных чисел берёт обычный остаток, для
нуля возвращает 0, для отрицательных сначала берёт остаток, а потом переводит его в эквивалентный
представитель в промежутке от 0 до d − 1.

14.

Исследование - Очевидное расширение на Z/dZ
После такого преобразования термы сложения P+Z/dZ и вычитания P-Z/dZ
считаются как сумма или разность в Z и затем берём остаток.
Но такой подход неэффективен: каждая операция всё равно использует
тяжелый примитивно-рекурсивный оператор остатка и сначала работает в
Z, а только потом проецируется результат в Z/dZ, вместо прямых
вычислений в самом кольце вычетов.

15.

Исследование - Проективные вычеты
В системе вычетов Z/dZ проекторы нужны затем, чтобы удобно выбирать отдельные
компоненты из набора аргументов и использовать циклическую структуру.
Проектор:
Uik x1 … xk = xi (для 1 ≤ i ≤ k).
Полу-проектор:
Vik x0 … xk-1 = xk xk+1 … xi-1 x0 … xk-1.
Проективные числа:
ī в Z/dZ определяется как Uid.

16.

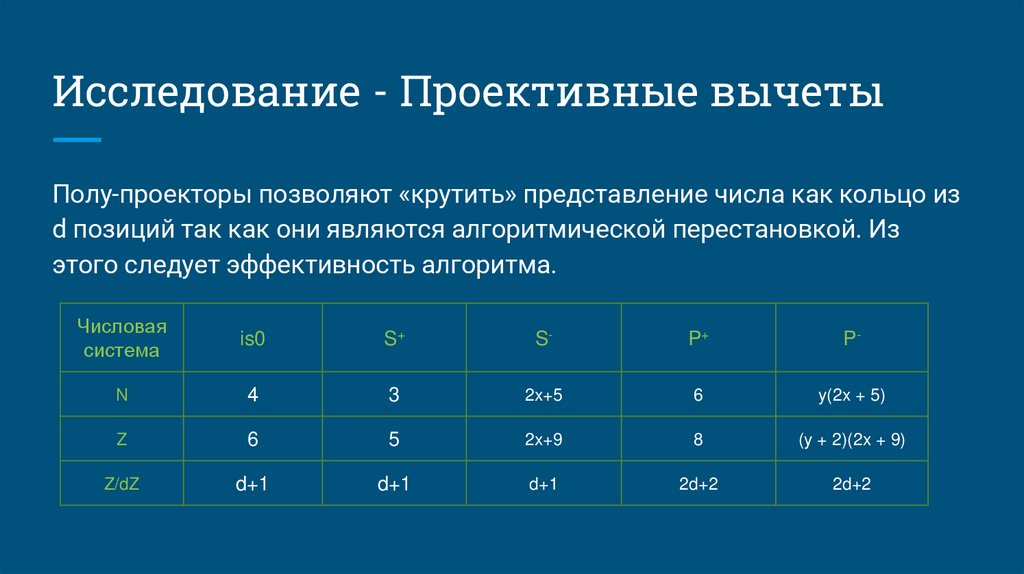
Исследование - Проективные вычеты
Полу-проекторы позволяют «крутить» представление числа как кольцо из
d позиций так как они являются алгоритмической перестановкой. Из
этого следует эффективность алгоритма.
Числовая
система
is0
S+
S-
P+
P-
N
4
3
2x+5
6
y(2x + 5)
Z
6
5
2x+9
8
(y + 2)(2x + 9)
Z/dZ
d+1
d+1
d+1
2d+2
2d+2

17.

Исследование - Бинарное лямбда исчисления
Мы узнали что через λ-выражения можно создавать числовую системы,
булеву логику и пора определить двоичную систему. Это нужно, потому
что компьютеры понимают только 0 и 1 и если определить λ-выражения
через это же 0 и 1, то можно создавать вычислительную технику на
лямбда анализе. Ученый De Bruijn сделал следующую рекурсию:
λx.00x, λxy.01xy, i = 1i0 где i это числа Чёрча
Таким образом, каждый комбинатор можно представить как двоичное
число.

18.

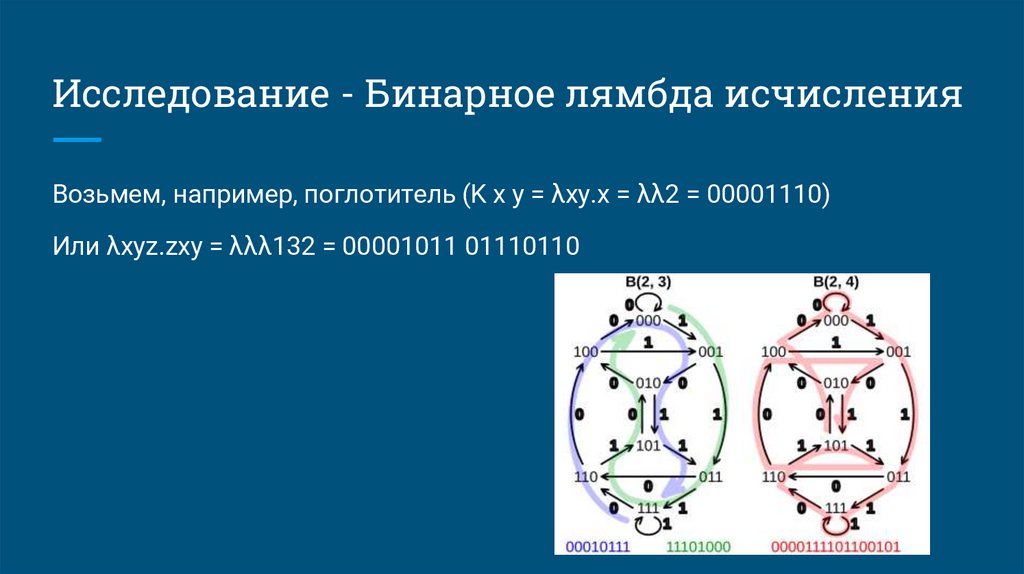
Исследование - Бинарное лямбда исчисления
Возьмем, например, поглотитель (K x y = λxy.x = λλ2 = 00001110)
Или λxyz.zxy = λλλ132 = 00001011 01110110

19.

Исследование - ФП

20.

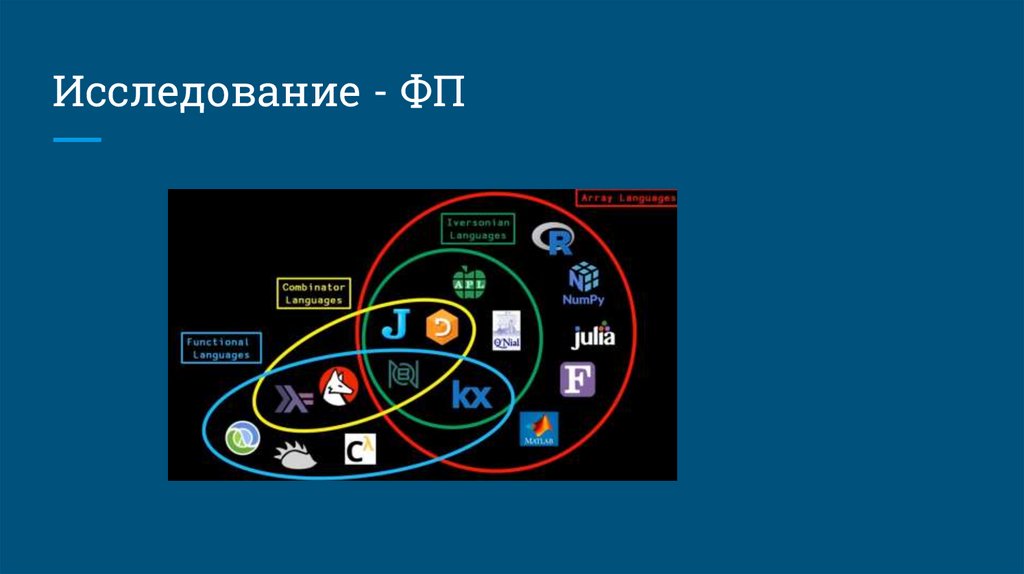
Исследование - ФП
Существует целый тип языков программирования (ЯП) которые
построены на λ выражениях: функциональные и массивного типа. Самые
известные функциональные: Haskell, F#, Kotlin. Масивного типа: APL, BQN,
J, Uiua.

21.

Исследование - ФП
Существуют разные подходы к бинаризации термов в бинарном λисчислении:
○ ООП реализация на привычных языках (например, через деревья)
дает относительно тяжелую, вплоть до квадратичной, асимптотику по
размеру терма.
○ ФП реализация на Rust позволяет опустить сложность до
квазилинейной.
○ Отдельно стоит реализация на языке программирования Uiua, APL и
тп, где каждый комбинатор — это глиф (иероглиф) и достаточно
нового вида данных - вектор глубин.
(λx.λy.x)(λx.(λz.z)x)(λa.a) -> [[1 2 3 1 2 3 2 1 2] [0 0 2 0 0 1 1 0 1]]

22.

Исследование - ФП реализация

23.

Материалы
Combinatory Logic and Combinators in Array Languages - Conor Hoekstra - conorhoekstra@gmail.com
Lambda Calculus - CSE 340 – Principles of Programming Languages
Lambda Calculus - Mattox Beckman - https://uiuc-cs421-sp22.netlify.app/handouts/lambda-calculus.pdf
Lambda Calculus - Steven Syrek - https://github.com/sjsyrek/presentations/blob/master/lambda-calculus/slides.md
Combinators - Pol Dellaiera - https://github.com/loophp/combinator/blob/master/README.md
Русская литература:
Ламбда-исчисления, его синтаксис и семантика - Х. Барендрегх (перевод)
Комбинаторная логика - В. Э. Вольфенгаген - (перевод)

24.

Спасибо за внимание!