ДЗ ньютона_bec734165cb406e76199557d644689c3

1.

2. Проверка домашнего задания

Решите уравнение:
1.
Ax2C xx 1 48
Ответ: x=4
2. C 1x 6C x2 6C x3 9 x 2 14 x
Ответ: x=7
x 2
3
C
2
C
3.
x 1
x 1 7( x 1)
Ответ: x=5
4.
Ax4
24
Ax3 1 C xx 4 23
Ответ: x=5
5.
Px 2
210
x 4
Ax 1 P3
Ответ: x=5
x 1
6. Ax 1 2 Px 1
30
Px
7
Ответ: x=7
Abramova N.K.
Abramova N.K
2

3. Проверка домашнего задания

Используя свойство числа сочетаний, найти значение выражения:
7.
10
11
a )C13
C13
Ответ: 364
б )C143 C142
Ответ: 455
в)C40 C41 С42 С43 С44
Ответ: 16
г )C74 C75 С76 С77
Ответ: 64
Abramova N.K.
Abramova N.K
3

4. Бином

Бином (лат. bis - два, nomen - имя) или двучлен —
частный случай многочлена (полинома), который состоит из
двух слагаемых одночленов (мономов).
Например:
a+b,
a-b,
a2 +b2,
Abramova N.K.
3b-4b3
Abramova N.K
4

5. Формулы сокращенного умножения

(a + b)2 = a2 + 2ab + b2
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
n=0
n=1
n=2
n=3
n=4
1
1
1
1
1
1
2
3
4
1
3
6
1
4
1
5-я строка (n=4) получается так:
1, 4=1+3, 6=3+3, 4=3+1, 1
Abramova N.K.
Abramova N.K
5

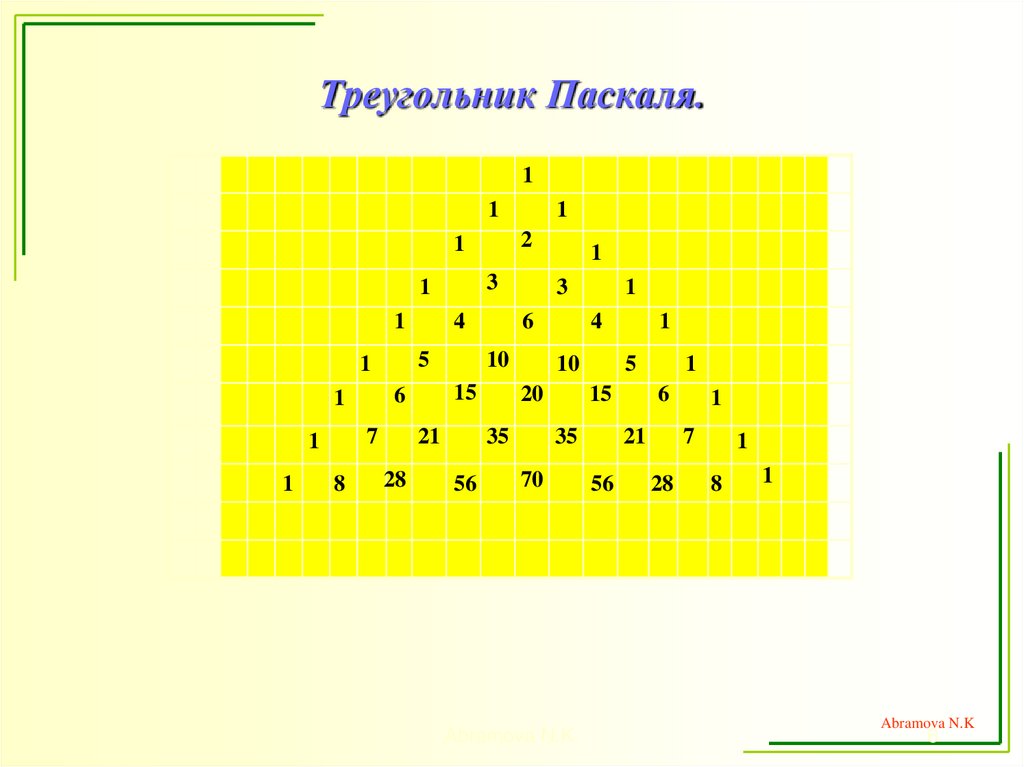
6. Треугольник Паскаля.

1
1
2
1
3
1
1
7
1
8
28
3
10
21
1
4
10
20
35
56
1
6
15
6
1
1
4
5
1
1
1
5
15
35
70
Abramova N.K.
1
6
21
56
1
7
28
1
8
1
Abramova N.K
6

7. Разложение бинома с помощью треугольника Паскаля.

Пример 1
(a b) 7 1 a 7 7 a 6 b1 21 a 5 b 2 35 a 4 b 3
35 a 3 b 4 21 a 2 b 5 7 a1 b 6 1 b 7
a 7 7a 6b 21a 5b 2 35a 4b 3 35a 3b 4 21a 2b 5 7ab 6 b 7
Abramova N.K.
Abramova N.K
7

8. Разложить бином с помощью треугольника Паскаля.

Задание 1
(1 x) 7
Задание 2
(2 x 3) 4
Abramova N.K.
Abramova N.K
8

9. Биномиальные коэффициенты

В основе построения треугольника Паскаля лежит свойство
сочетаний Cmn 11 Cmn Cmn 1.
Поэтому коэффициенты разложения степени бинома можно
записать с помощью числа сочетаний:
(a b)1 C10 a C11b
(a b) 2 C20 a 2 C21ab C22b 2
(a b)3 C30 a 3 C31a 2b C32 ab 2 C33b 3
(a b) 4 C40 a 4 C41a 3b C42 a 2b 2 C43 ab 3 C44b 4
Abramova N.K.
Abramova N.K
9

10. Общий вид биномиальной формулы Ньютона

(a b) m Cm0 a m Cm1 a m 1b Cm2 a m 2b 2 ... Cmm 1ab m 1 Cmmb m
Бином Ньютона –формула, выражающая целую положительную степень
суммы двух слагаемых (двучлена, бинома) через степени этих слагаемых.
Частными случаями бинома Ньютона являются формулы квадрата
и куба суммы двух слагаемых a и b
Abramova N.K.
Abramova N.K
10

11. Свойства разложения бинома

(a b) m Cm0 a m Cm1 a m 1b Cm2 a m 2b 2 ... Cmm 1ab m 1 Cmmb m
1. Число всех членов разложения на единицу больше показателя бинома.
2. Сумма показателей степеней a и b каждого члена разложения равна
показателю степени бинома
3. Общий член разложения имеет вид:
Tk 1 Cmk a m k b k
4. Сумма коэффициентов разложения (a+b)m равна 2m.
5. Биномиальные коэффициенты членов, равноотстоящих от концов
разложения равны
Cmk Cmm k
Abramova N.K.
Abramova N.K
11

12. Блез Паскаль и его треугольник.

На рисунке справа изображено несколько
строк числового треугольника, образованного по следующему правилу:
по краям каждой строки стоят единицы,
а каждое из остальных чисел равно сумме двух
стоящих над ним чисел предыдущей строки.
В такой форме треугольник приведен в
«Трактате об арифметическом треугольнике»
французского математика Б.Паскаля (1623-1662),
опубликованном в 1665 году уже после смерти автора.
Несколько иные варианты этой числовой
таблицы встречались столетием раньше
у итальянского математика Н.Тартальи, а
за несколько веков до этого у среднеазиатского
ученого и поэта Омара Хайяма, некоторых
китайских и индийских ученых.
Abramova N.K.
Abramova N.K
12

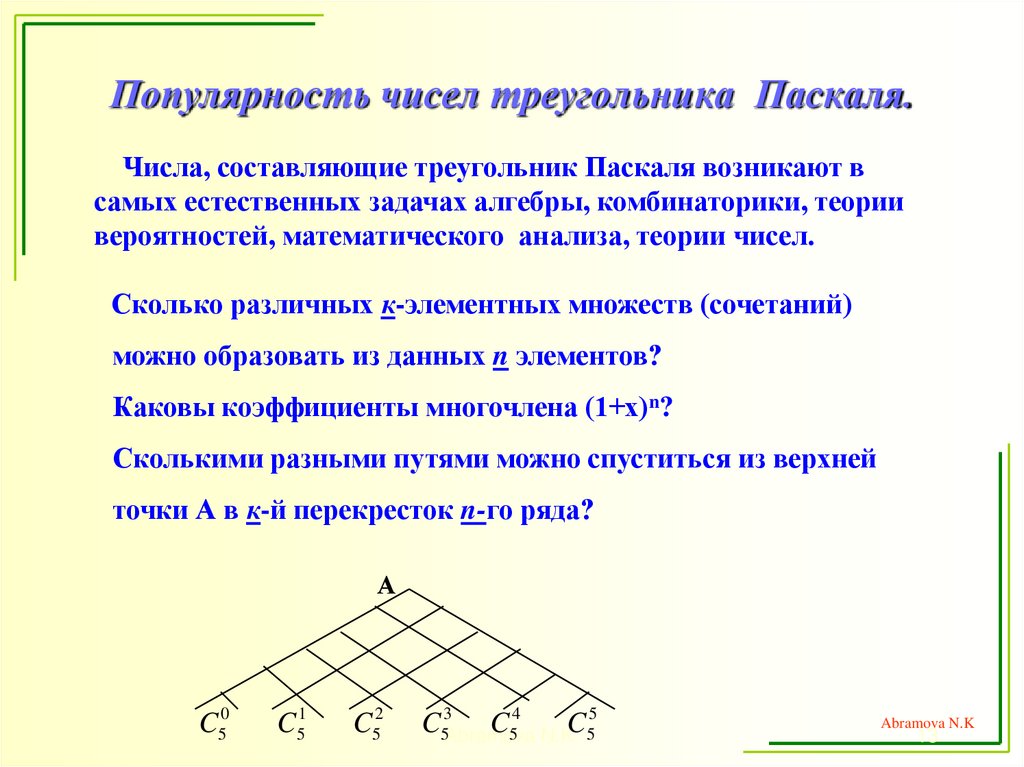
13. Популярность чисел треугольника Паскаля.

Числа, составляющие треугольник Паскаля возникают в
самых естественных задачах алгебры, комбинаторики, теории
вероятностей, математического анализа, теории чисел.
Сколько различных к-элементных множеств (сочетаний)
можно образовать из данных n элементов?
Каковы коэффициенты многочлена (1+х)n?
Сколькими разными путями можно спуститься из верхней
точки А в к-й перекресток n-го ряда?
А
C50
C51
C52
C53Abramova
C54 N.K.C55
Abramova N.K
13

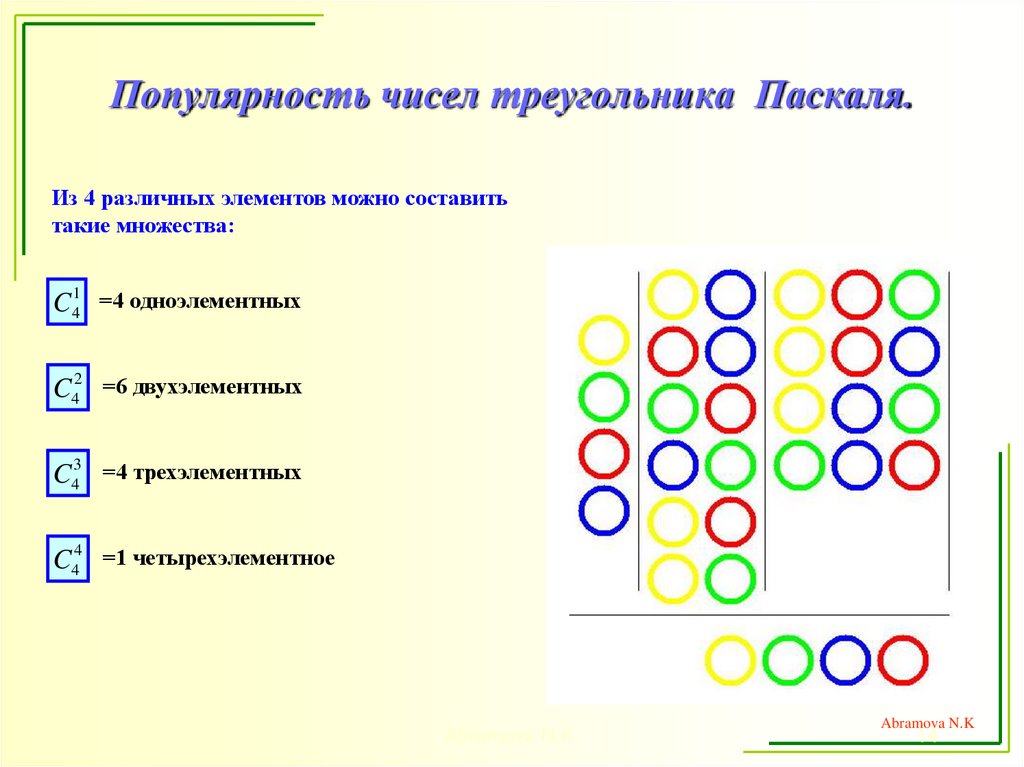
14. Популярность чисел треугольника Паскаля.

Из 4 различных элементов можно составить
такие множества:
C41 =4 одноэлементных
C42 =6 двухэлементных
C43 =4 трехэлементных
C44 =1 четырехэлементное
Abramova N.K.
Abramova N.K
14

15. Бином Ньютона.

В 1664-1665 г.г. И.Ньютон установил,
что формула выражающая степень
двучлена в виде суммы одночленов
обобщается на случай произвольных
(дробных и отрицательных) показателей
Исаак Ньютон
1643-1727
Abramova N.K.
Abramova N.K
15

16. Бином Ньютона в художественной литературе

Бином Ньютона появляется в нескольких запоминающихся контекстах,
где речь идет о чем-либо сложном.
В рассказе А. Конан Дойля «Последнее дело Холмса» Холмс говорит о
математике профессоре Мориарти:
«Когда ему исполнился двадцать один год, он написал трактат о биноме
Ньютона, завоевавший ему европейскую известность. После этого он
получил кафедру математики в одном из наших провинциальных
университетов, и, по всей вероятности, его ожидала блестящая
будущность».
Знаменита цитата из «Мастера и Маргариты» М. А. Булгакова:
«Подумаешь, бином Ньютона!».
Abramova N.K.
Abramova N.K
16

17. P.S.

H
S(х)
P.S.
х
Считай несчастным тот день
или час, в который ты не
усвоил ничего нового и ничего
не прибавил к своему
образованию.
Ян Амос Коменский
Abramova N.K.
Abramova N.K
17