Свойства биноминальных коэффициентов. Бином Ньютона

1.

Свойства биномиальных
коэффициентов
Цель: познакомиться со свойствами
биноминальных коэффициентов;
научить применять формулу бинома Ньютона
при возведении в степень двучлена;

2.

Бином Ньютона

3.

Основные свойства
биномиальных коэффициентов:

4. Бином Ньютона.

Бином (лaт. bis − два, nomen - имя)
или двучлен — частный случай
многочлена (полинома), который
состоит из двух слагаемых
одночленов (мономов).
Например:
a + b,
a − b,
a2 + b2,
3b −4b3

5.

Степени суммы двух чисел:
а b 1
1
а b 1 а 1 b
2
2
2
а b 1 а 2 аb 1 b
3
3
2
2
3
а b 1 а 3 а b 3 аb 1 b
4
а b 1 а 4 4 а 3b 6 а 2b 2 4 аb3 1 b 4
0
а b
5
1 а 5 5 а 4b1 10 а 3b 2 10 а 2b 3 5 а1b 4 1 b 5
Составим таблицу из коэффициентов в
записанных суммах

6.

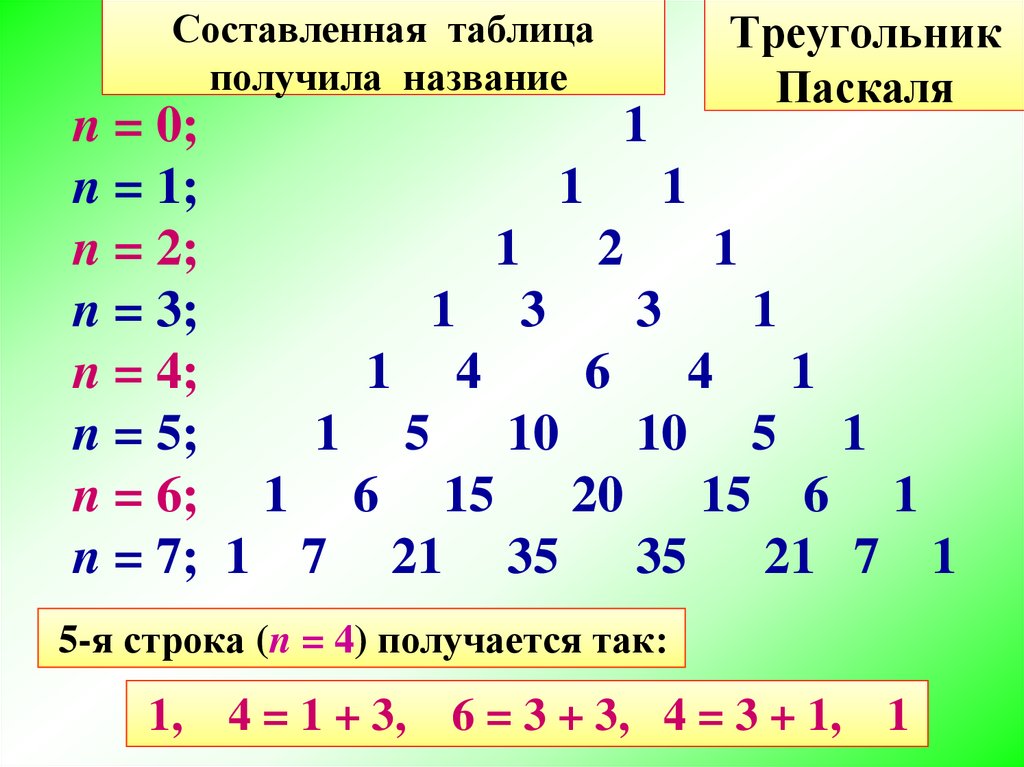
Составленная таблица
получила название
Треугольник
Паскаля
n = 0;
1
n = 1;
1
1
n = 2;
1
2
1
n = 3;
1 3
3
1
n = 4;
1 4
6
4 1
n = 5;
1 5
10
10 5 1
n = 6; 1 6 15
20
15 6 1
n = 7; 1 7 21 35
35
21 7 1
5-я строка (n = 4) получается так:
1, 4 = 1 + 3, 6 = 3 + 3, 4 = 3 + 1, 1

7. Разложение бинома с помощью треугольника Паскаля.

Коэффициенты 7 строки:
1; 7; 21; 35; 35; 21; 7; 1
Пример 1
(a b) 1 a 7 a b 21 a b 35 a b
7
7
6
1
5
2
4
3
35 a 3 b 4 21 a 2 b5 7 a1 b 6 1 b 7
a 7 7a 6b 21a 5b 2 35a 4b3 35a 3b 4 21a 2b5 7ab 6 b 7

8.

Пример 2
Коэффициенты 7 строки:
1; 7; 21; 35; 35; 21; 7; 1
(1 x) 7 1 17 7 16 x1 21 15 x 2 35 14 x 3
35 13 x 4 21 12 x 5 7 11 x 6 1 x 7
1 7 x 21x 2 35 x 3 35 x 4 21x 5 7 x 6 x 7
Коэффициенты 4 строки:
Пример 3
1; 4; 6; 4; 1
(2 x 3) 4 1 (2 x) 4 4 (2 x)3 31 6 (2 x) 2 32
4 (2 x)1 33 1 34
16 x 96 x 216 x 216 x 81
4
3
2

9. Биномиальные коэффициенты

В основе построения треугольника Паскаля
лежит свойство сочетаний
C
n 1
m 1
C C
n
m
n 1
m
.
Поэтому коэффициенты разложения степени
бинома можно записать с помощью числа
сочетаний

10.

Степени суммы двух чисел:
а b
1
1 а 1 b
С 1; С 1
0
1
1
1
а b
1
а b
и
a 1; b 1, тогда
0
0
С а b С а b
0 1 0
1
1 0 1
1
С 1; С 2; С 1
0
2
Аналогично:
2
Заметим, что
1
2
2
2
С а b С а b С а b
0
2
2 0
1 1 1
2
2
2
0 2
С 1; С 3; С 3; С 1
0
3
1
3
а b
3
2
3
3
3
С а b С а b С а b С а b и т. д.
0 3 0
3
1 2 1
3
2 1 2
3
3 0 3
3

11. Правило Паскаля:

С
C
n
m 1
n 1
m
C
n
m
Биноминальные коэффициенты:
m!
С
n!(m n)!
n
m
C C 1;
0
m
С
n
m 1
C C
m
m
C
n 1
m
1
m
C ;
n
m
С C ... C
0
m
1
m
С
m 1
m
n
m 1
m 1
m
m;
C
n 1
m 1
C ;
C 2
m
m
n
m
m

12. Бином Ньютона:

а b
т
С а b C a
0
m
m 0
1
m
m 1 1
b ... C
m 1 1 m 1
m
ab
C a b
m
m
0 m
Бином Ньютона – формула, выражающая целую
положительную степень суммы двух слагаемых
(двучлена, бинома) через степени этих слагаемых.
Частными случаями бинома Ньютона являются
формулы квадрата и куба суммы
двух слагаемых a и b

13.

Применение формулы бинома Ньютона
Пример 4
1
1 2
1 5
1
4
2
3
5
(2a ) (2a ) C5 (2a) ( ) C5 (2a) ( )
2
2
2
1 3
1 4
1 5
4
1
C ( 2 a ) ( ) C5 ( 2 a ) ( ) ( )
2
2
2
5
1
5
4
3
2
32a 40a 20a 5a a
8
32
3
5
2

14. Самостоятельная работа Задание 1. Найти разложение бинома

15. Задание 2.

У многочлена P(x) найдите коэффициент
при:
Задание 3.
4Р3+3А210-С25

16.

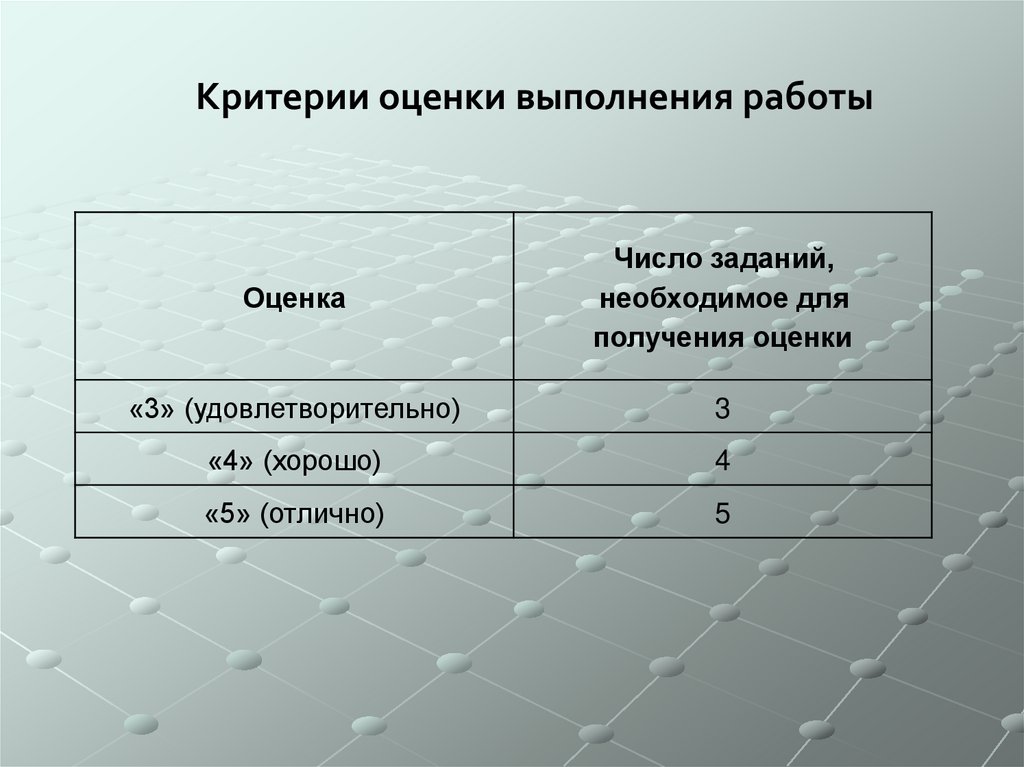
Критерии оценки выполнения работы
Оценка
Число заданий,
необходимое для
получения оценки
«3» (удовлетворительно)
3
«4» (хорошо)
4
«5» (отлично)
5