presentation (2)

1.

Использование интегралов в
высшей математике
Кафедра математического анализа

2.

Введение: Интегралы в математике
Интегральное исчисление — фундаментальный раздел математического анализа,
имеющий широкое применение в науке и технике.
• Определенный интеграл — площадь под кривой
• Неопределенный интеграл — первообразная функции
• Несобственные интегралы — расширение понятия
• Кратные интегралы — интегрирование по областям
• Криволинейные интегралы — интегрирование вдоль кривых
0.3cm
Формула Ньютона-Лейбница:
$$\int_{a}^{b} f(x)dx = F(b) - F(a)$$

3.

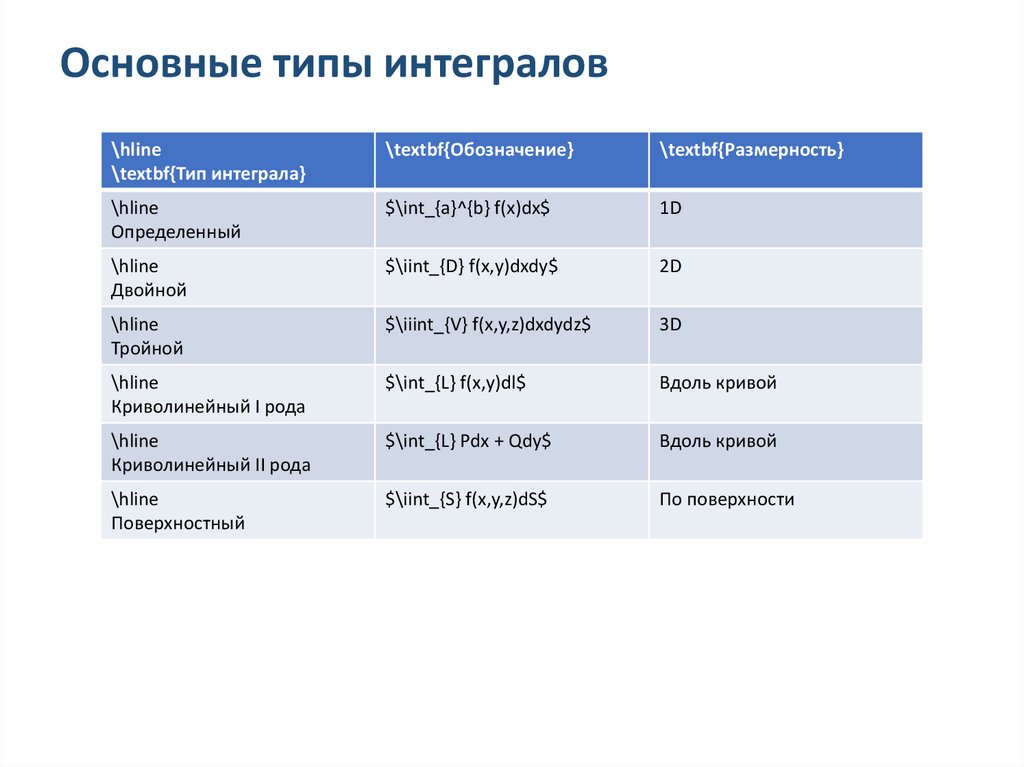
Основные типы интегралов
\hline
\textbf{Тип интеграла}
\textbf{Обозначение}
\textbf{Размерность}
\hline
Определенный
$\int_{a}^{b} f(x)dx$
1D
\hline
Двойной
$\iint_{D} f(x,y)dxdy$
2D
\hline
Тройной
$\iiint_{V} f(x,y,z)dxdydz$
3D
\hline
Криволинейный I рода
$\int_{L} f(x,y)dl$
Вдоль кривой
\hline
Криволинейный II рода
$\int_{L} Pdx + Qdy$
Вдоль кривой
\hline
Поверхностный
$\iint_{S} f(x,y,z)dS$
По поверхности

4.

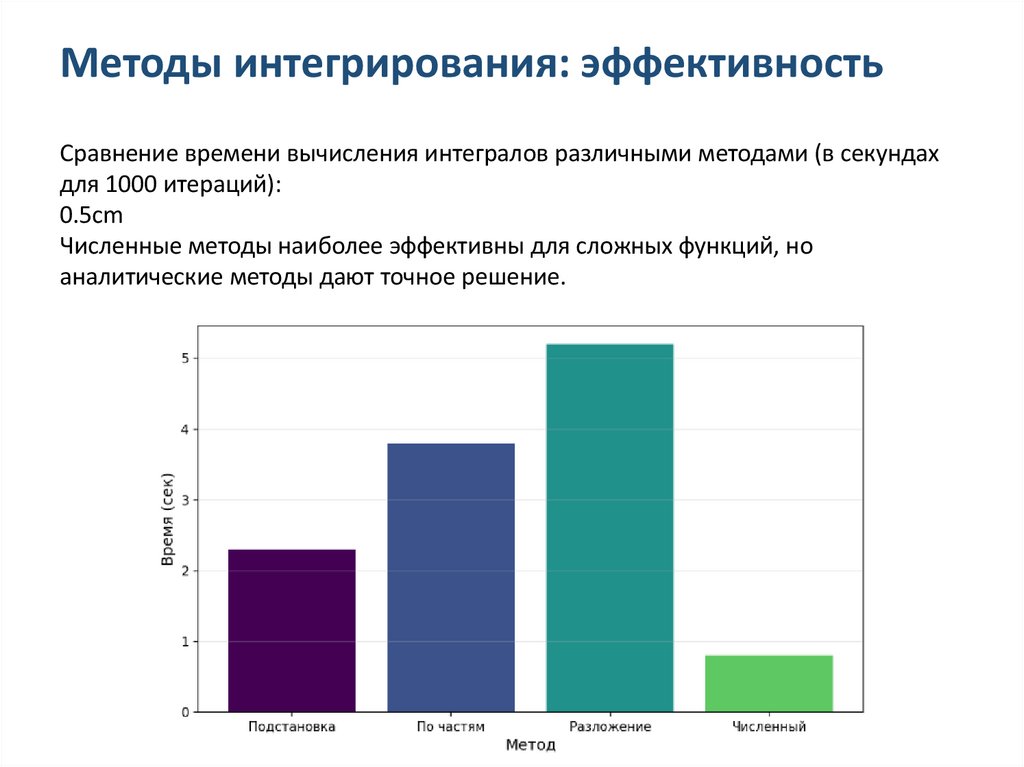
Методы интегрирования: эффективность
Сравнение времени вычисления интегралов различными методами (в секундах
для 1000 итераций):
0.5cm
Численные методы наиболее эффективны для сложных функций, но
аналитические методы дают точное решение.

5.

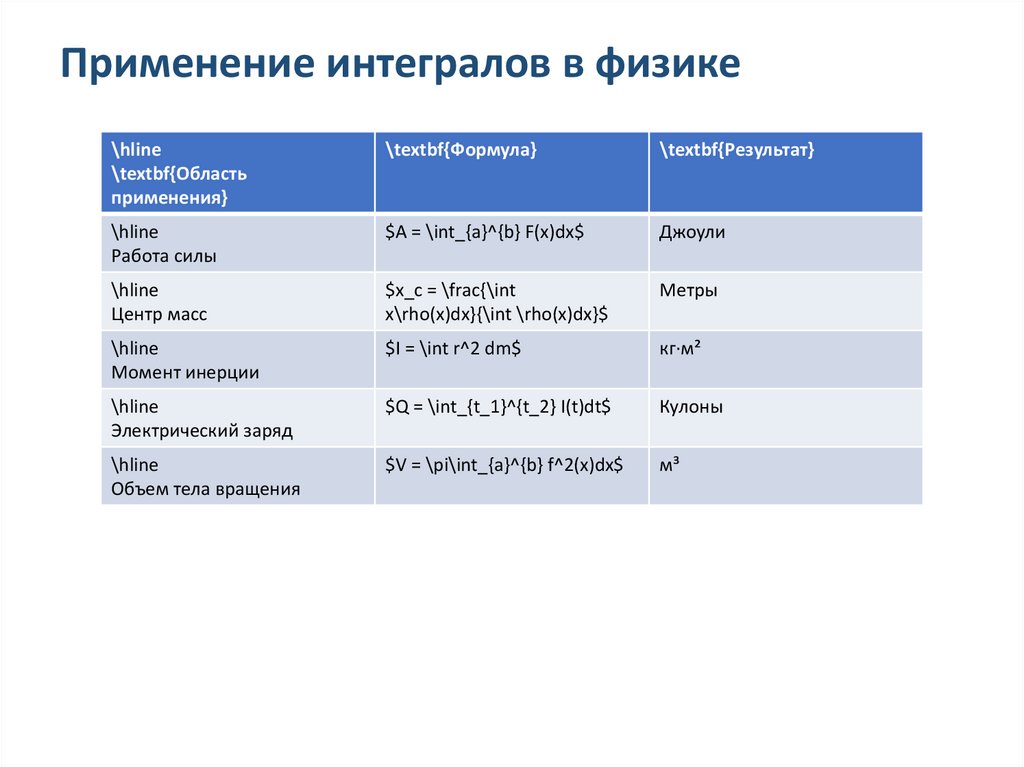
Применение интегралов в физике
\hline
\textbf{Область
применения}
\textbf{Формула}
\textbf{Результат}
\hline
Работа силы
$A = \int_{a}^{b} F(x)dx$
Джоули
\hline
Центр масс
$x_c = \frac{\int
x\rho(x)dx}{\int \rho(x)dx}$
Метры
\hline
Момент инерции
$I = \int r^2 dm$
кг·м²
\hline
Электрический заряд
$Q = \int_{t_1}^{t_2} I(t)dt$
Кулоны
\hline
Объем тела вращения
$V = \pi\int_{a}^{b} f^2(x)dx$
м³

6.

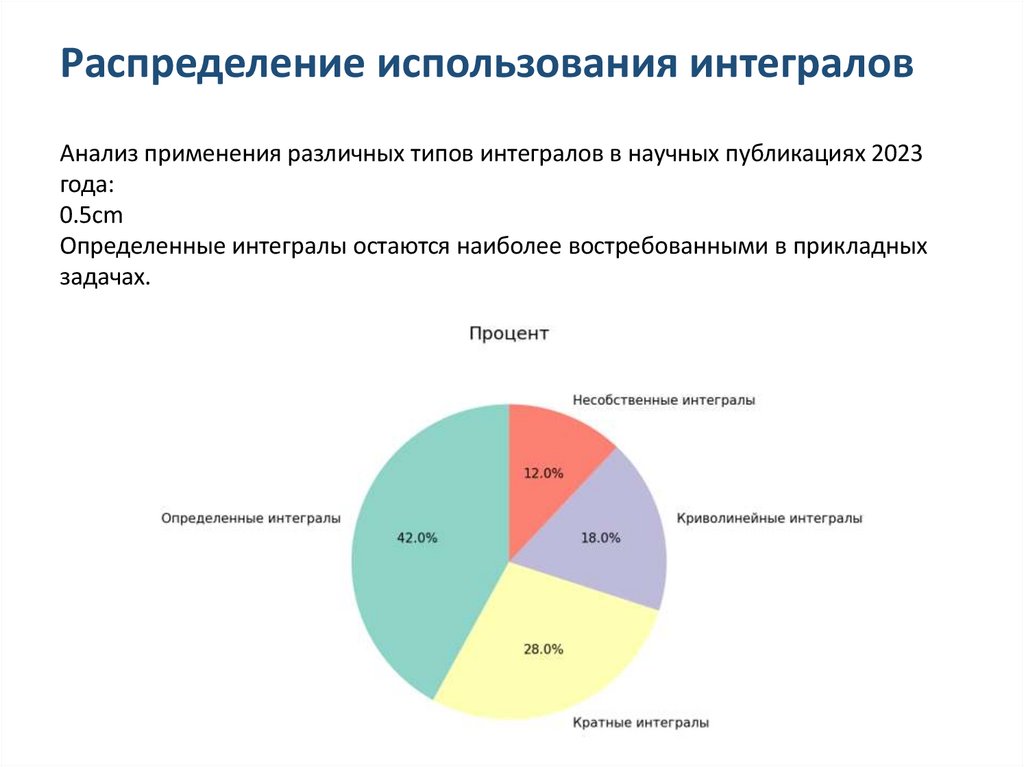
Распределение использования интегралов
Анализ применения различных типов интегралов в научных публикациях 2023
года:
0.5cm
Определенные интегралы остаются наиболее востребованными в прикладных
задачах.

7.

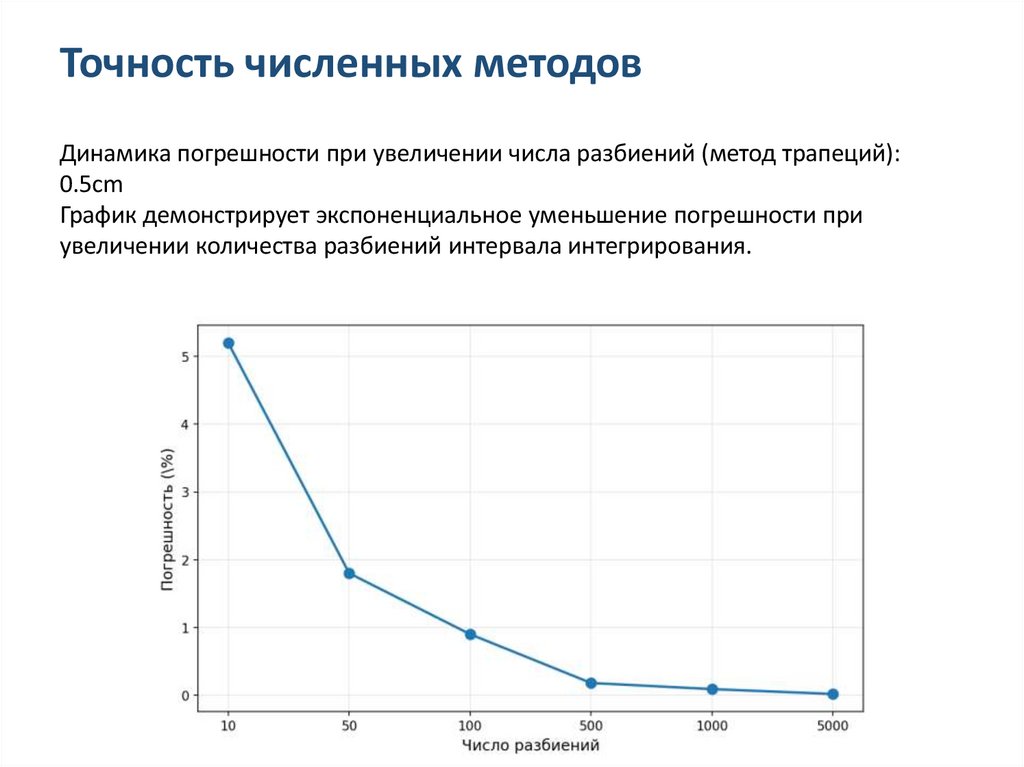
Точность численных методов
Динамика погрешности при увеличении числа разбиений (метод трапеций):
0.5cm
График демонстрирует экспоненциальное уменьшение погрешности при
увеличении количества разбиений интервала интегрирования.

8.

Заключение
Ключевые выводы:
• Интегралы — универсальный инструмент для решения задач в математике, физике и
инженерии
• Выбор метода интегрирования зависит от типа функции и требуемой точности
• Численные методы эффективны для сложных функций
• Кратные интегралы необходимы для многомерных задач
• Современные вычислительные системы позволяют решать сложнейшие интегральные
уравнения
0.5cm
Спасибо за внимание!