Similar presentations:
ГЂ†Ґ†3-з†бвм2
1. Курс «Математическое моделирование процессов в природных, социально-экономических средах»
КУРС«МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ПРОЦЕССОВ В ПРИРОДНЫХ,
СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ СРЕДАХ»
2. Глава 3 МЕТОДЫ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
ГЛАВА 3МЕТОДЫ ПОСТРОЕНИЯ
МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
Часть 2
2
3.
3. Метод вариационных принципов и математические моделиВариационные
принципы
представляют
собой
общие
утверждения о рассматриваемом объекте (явлении, системе) и
гласят, что из всех возможных вариантов его поведения
(эволюции,
движения)
выбирают
лишь
те,
которые
удовлетворяют определенному условию.
3
4.
Согласно этому условию некоторая связанная с объектомвеличина достигает экстремального значения при его переходе из
одного состояния в другое.
Применение вариационных принципов – эффективный подход к
построению математических моделей, по своей широте и
универсальности сопоставимый с возможностями, даваемыми
фундаментальными законами.
4
5.
3.1. Принцип ФермаВпервые вариационный принцип был открыт Героном при
изучении отражения света. Этот принцип основан на том, что в
природе
события
осуществляются
наиболее
легкими
и
доступными путями.
5
6.
Аналитический вид вариационногопринципа
проблемы
Пьером
для
был
Ферма
физической
сформулирован
г.).
(1660
принцип заключается
в
Этот
том,
что действительный путь распространения света 2 есть тот, для
прохождения которого свету требуется минимальное время по
сравнению с другими мыслимыми путями 1, 3, 4 между теми же
точками (рис. 1).
6
7.
Из определения скорости v = ds /dt находимA1
ds
t ,
v
A0
где А0 и A1 начальные и конечные точки.
Из условия минимума получаем математическую трактовку
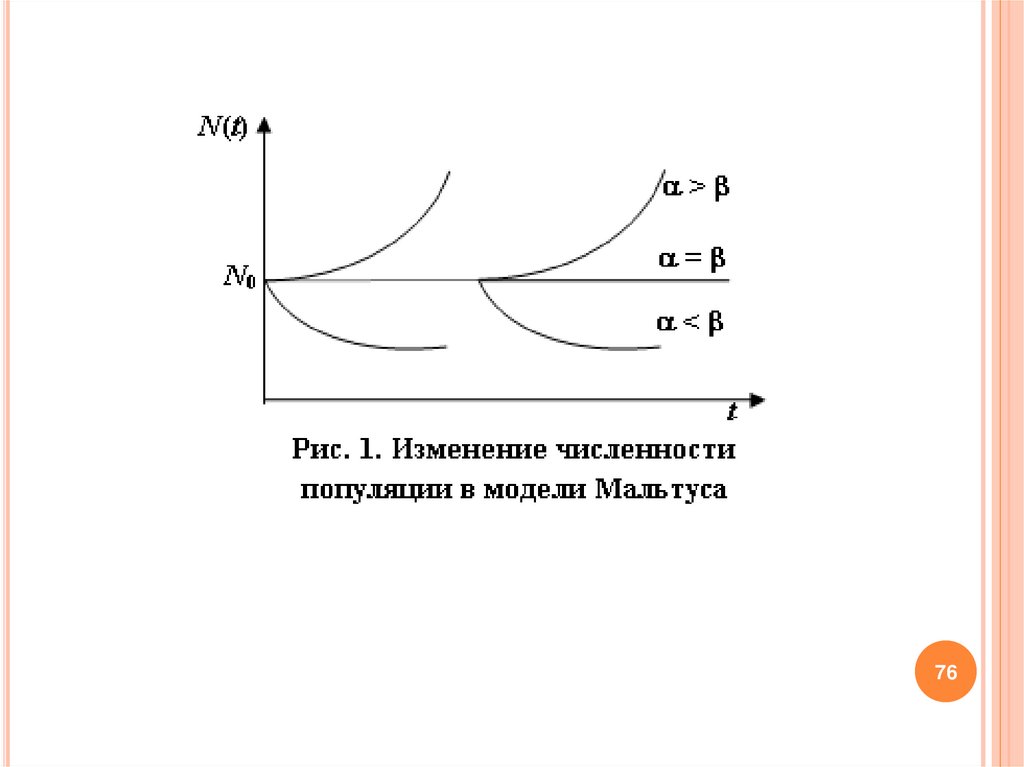
вариационного принципа Ферма:
A1
ds
0.
v
A0
7
8.
Согласно принципу Ферма, луч света, выходящий из точки А0 ипопадающий в точку А1, избирает путь, время перехода по
которому является наименьшим.
8
9.
Пример 1.Используя вариационный принцип Ферма, получим основной
закон геометрической оптики (закон преломления).
9
10.
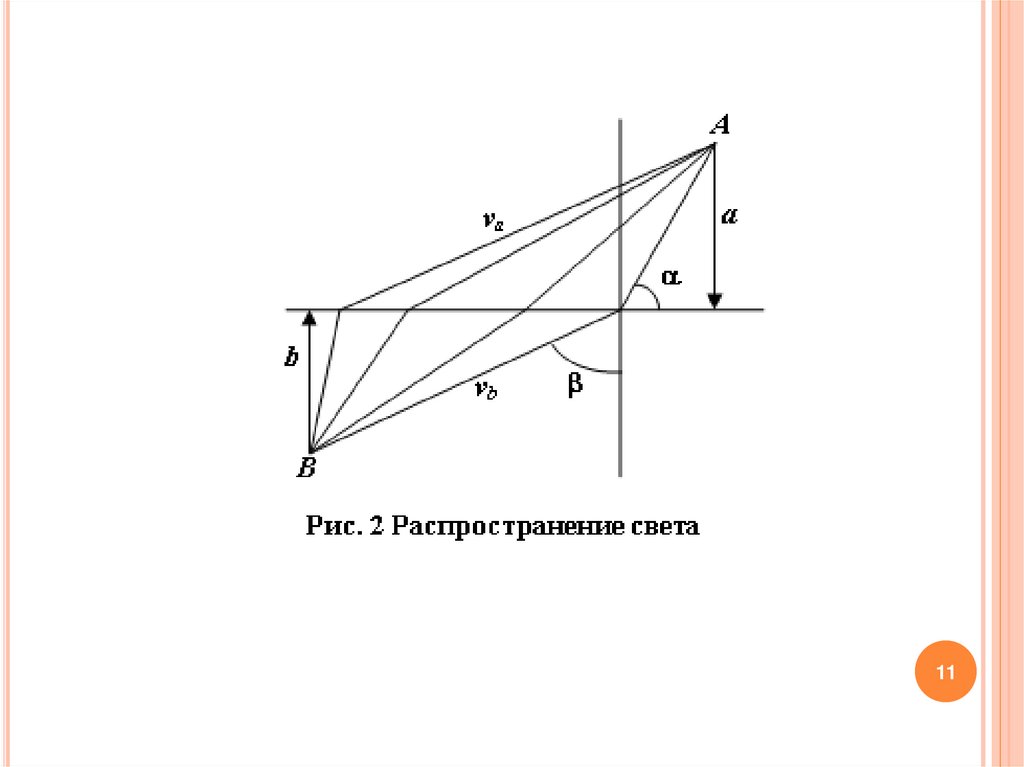
Свет, выходящий из точки А, движется в первой среде соскоростью va, преломляется и, переходя через линию раздела,
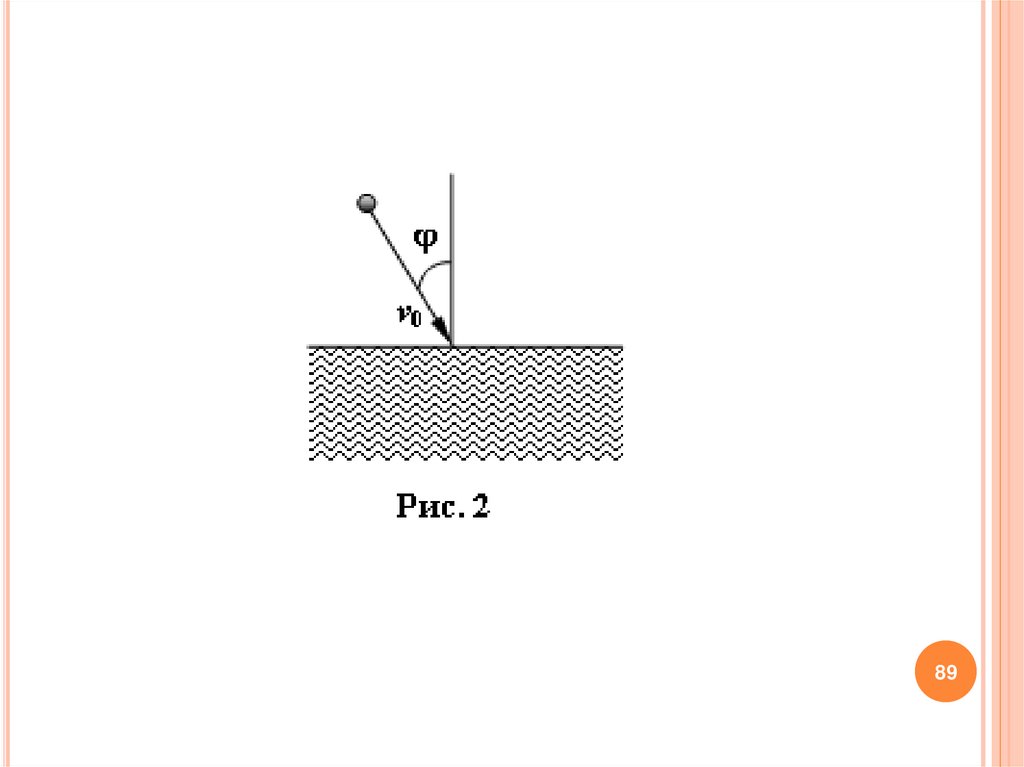
двигается во второй среде со скоростью vb и попадает в точку В.
Пусть - угол падения луча, а ( ) – угол его преломления
(рис. 2).
10
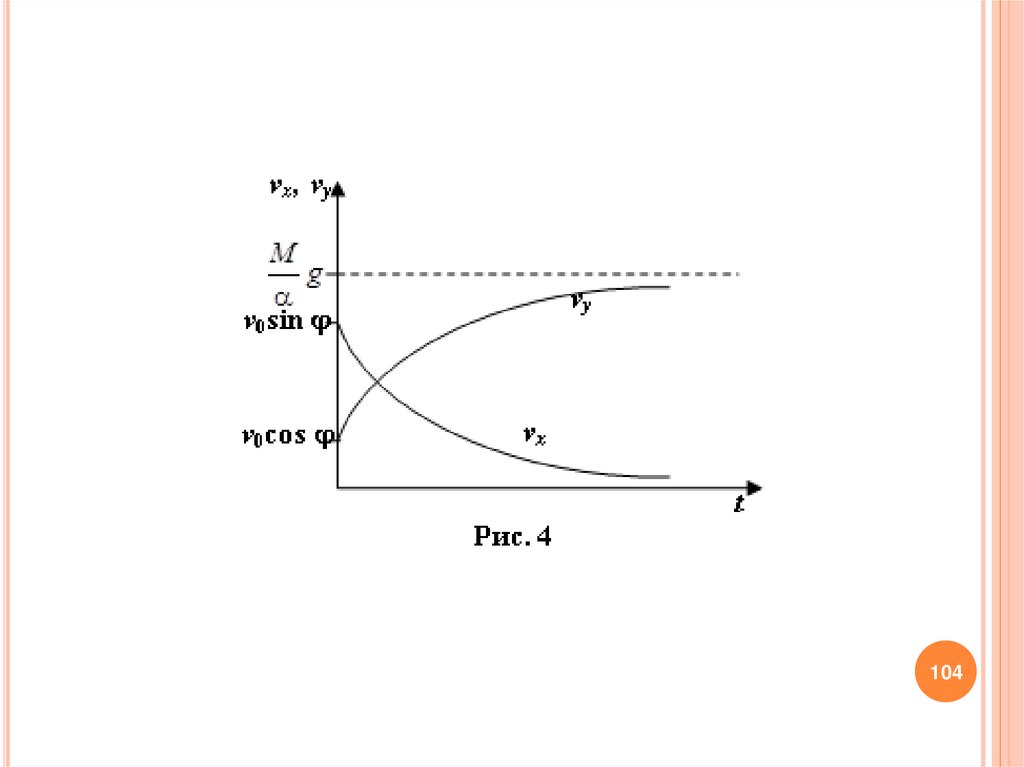
11.
1112.
Здесь а и b – длины перпендикуляров, опущенных из точки А и Вна прямую.
Время прохождения света из А в В равно
t ( )
a
b
,
va sin vb sin ( )
где va и vb – скорости света в первой и во второй средах.
Согласно
принципу
Ферма
свет
распространяется
за
минимальное время (рис. 2.).
12
13.
Условие минимальности имеет видdt
a cos
b cos d
0.
d v a sin v b sin ( ) d
(1)
Для любых значений справедливо равенство
C
a
b
const,
tg tg ( )
(2)
где С – расстояние между проекциями точек А и В на прямую
(одинаковое для всех траекторий).
13
14.
Дифференцируем (2):dC
a
b
d
2
0
2
2
2
d
tg cos tg cos ( ) d
d
0.
2
2
sin sin ( ) d
a
Исключаем из последней
b
формулы
производную
d
,
d
учитываем условие (1).
Отсюда получаем
cos va
.
cos vb
14
15.
Вводя понятия угла падения и преломления = 90 , = 90и выражая скорости распространения света в средах через
показатели преломления va = с/па, vb = с/пb, получаем основной
закон преломления, который обычно записывается в виде
sin v a nb
.
sin v b na
15
16.
Пример 1б. Закон отражения.Получить закон отражения, исходя из принципа Ферма.
16
17.
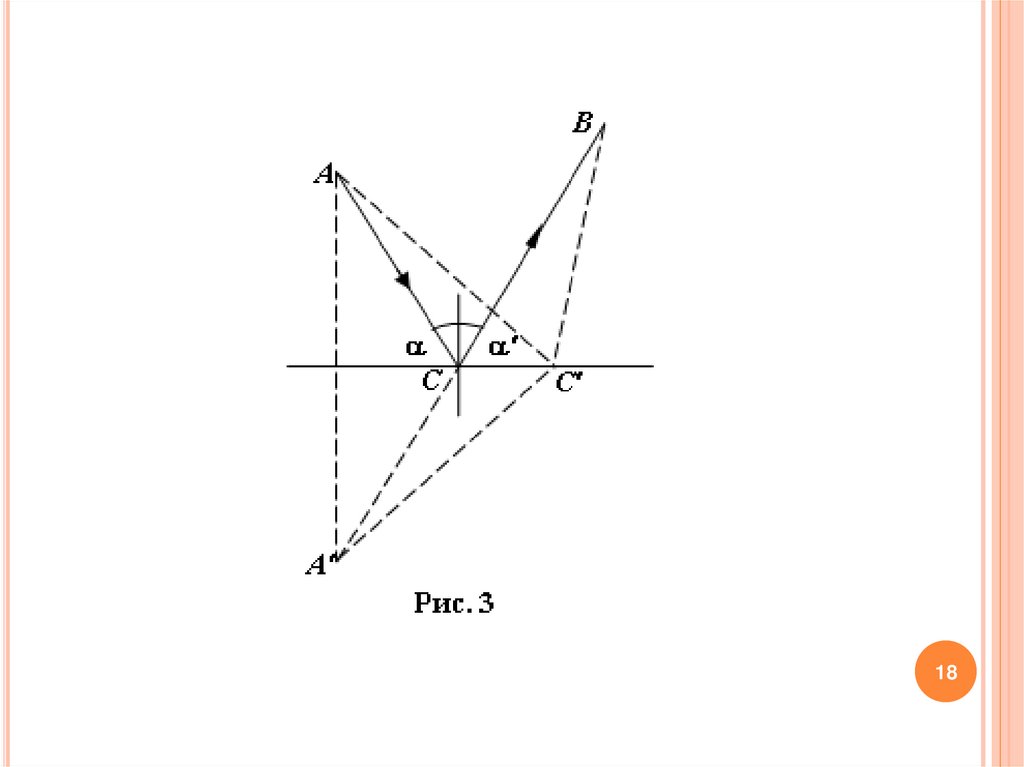
Получим закон отражения. Для этого рассмотрим ситуацию,когда свет должен попасть из точки А в точку В, испытав при
этом отражение от плоского зеркала (рис. 3). Среда, в которой
распространяется
оптической
свет,
длины
однородна,
пути
сводится
поэтому
к
минимальность
минимальности
его
геометрической длины.
17
18.
1819.
Введем вспомогательную точку А , являющуюся зеркальнымотражением точки А. Тогда из рис. 3 сразу следует, что самый
короткий путь из точки А в точку В с отражением от зеркала
будет в том случае, если отражение произойдет в точке С, для
которой выполняется условие = .
19
20.
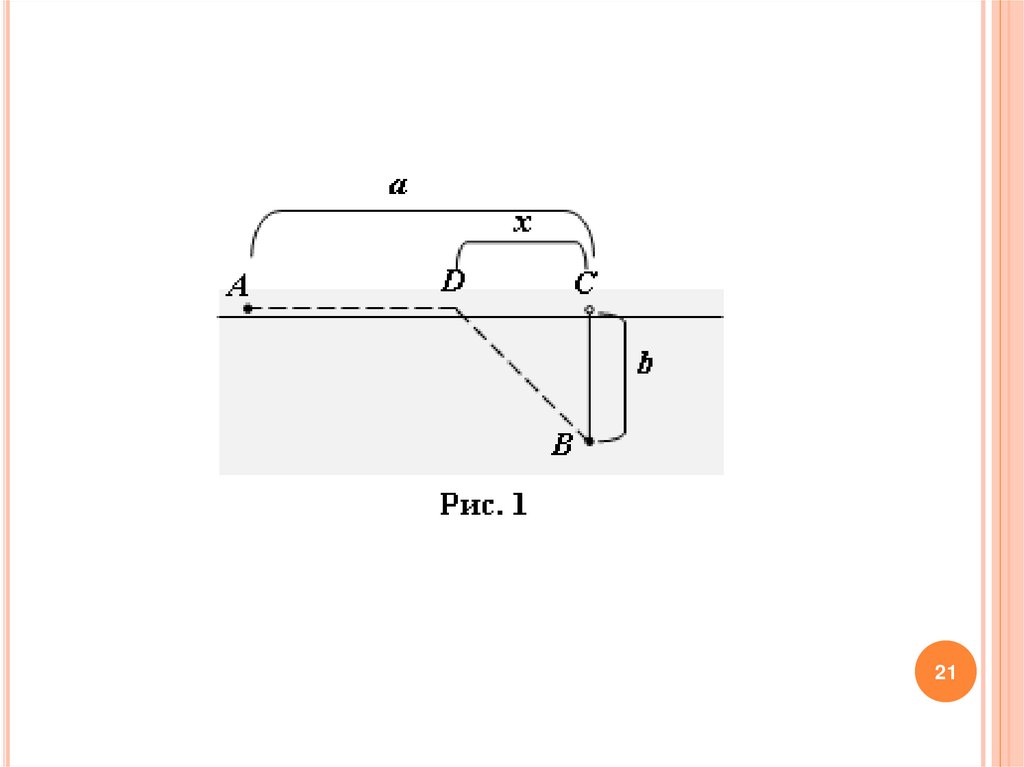
Пример 2.Вдоль кромки вспаханного поля проходит дорога, на которой
находится автобусная остановка А. План местности представлен
на рис. 1. Дом В находится в поле в 100 м (ВС) от дороги.
Расстояние от точки С до остановки 400 м. Найти минимальное
время, за которое человек может добраться от дома до
автобусной остановки, если по полю он может идти со скоростью
v1 =4,5 км/ч, а по дороге может бежать со скоростью v2 = 9 км/ч.
20
21.
2122.
РешениеВидимо человеку следует бежать «наискосок», в точку D.
Но как выбрать точку D, чтобы сэкономить время ?
Типичная задача на нахождение минимума функции. Время
движения на участке BD
t1
BD
v1
x 2 b2
,
v1
время на участке DA
t2
a x
v2
.
22
23.
Полное время движенияx 2 b2 a x
.
v1
v
T
Приравнивая
2
dT
dx
к нулю, находим положение точки D:
1
2v1
x
v1
2
2
x b
,
v2
1
0,
x 2 b 2 v2
2x
x2
v12
x 2 b2
2
2
2
2 v 2 v1 b
x
.
v 2v 2 v 2
1 2
2
v 22
,
23
24.
Учитывая, что по условиюv2 =2v1,
2
b2
2 3v1
x
,
4
2
4v1 4v1
3 x 2 b2 ,
x
b
.
3
24
25.
Подставим это значение х в выражение для полного временидвижения и вычислим Тmin:
Tmin
b2
b
b2 a
4b
3a b 1
3
3
( 3b a )
v1
v2
3v 2
3v 2
v2
1,73 100 400
229,2 с.
2,5
25
26.
Чисто математически мы не знаем, что мы нашли: минимум илимаксимум функции. Для этого надо бы ещё посчитать вторую
производную. Практический опыт и интуиция подсказывают, что
это минимум.
Сама по себе задача на нахождение минимума (или максимума)
функции
является
полезным
упражнением,
но
обычно
предпочитают простые решения.
Две среды: пахота и асфальт. Две скорости: v1 и v2. Что-то это
напоминает…
26
27.
В оптике мы знакомились с принципом Ферма: попадая из точкиА в точку В, свет выбирает путь, отнимающий наименьшее
время. Следствиями этого принципа являются все законы
геометрической оптики, в том числе и закон Снелла. На границе
раздела двух оптически прозрачных сред свет преломляется
согласно формуле:
sin v1
.
sin v 2
27
28.
При выводе формулы свойства света никак не использовались.А значит, она пригодна для движения любого тела, скорость
которого меняется при переходе из среды 1 в среду 2.
28
29.
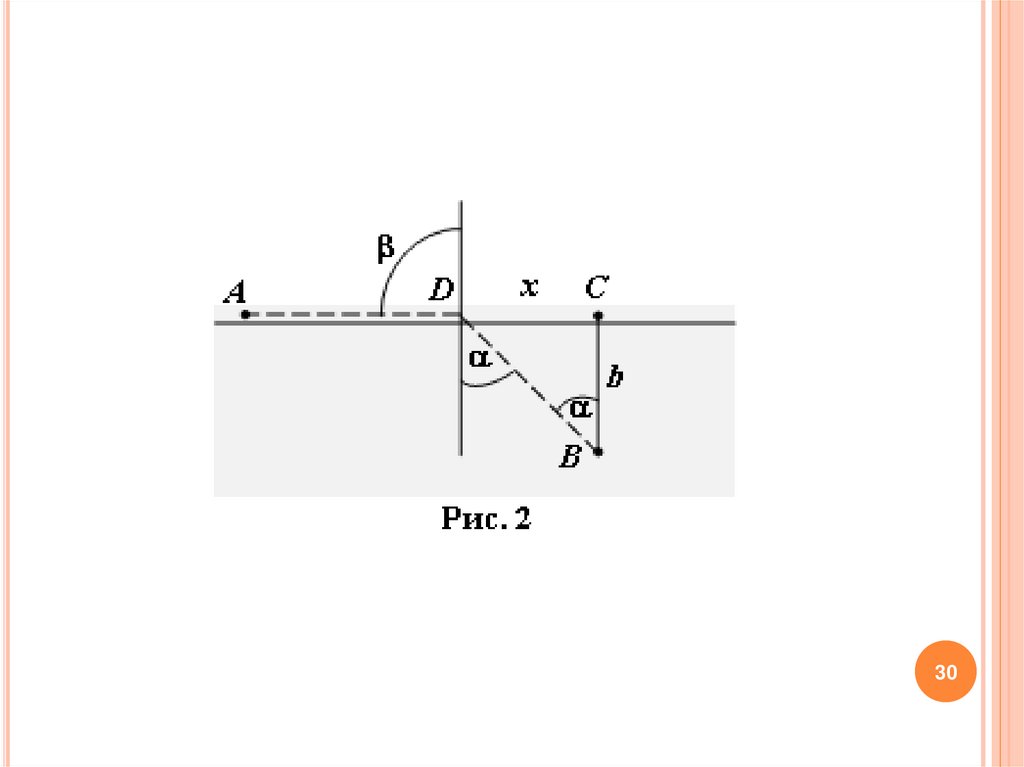
В нашей задаче угол между перпендикуляром к дороге инаправлением движения человека по полю, угол между
перпендикуляром и дорогой (рис. 2).
sin
v
1,
sin 90 v 2
4,5
1
sin
sin 90 .
9
2
Таким образом, =30 .
29
30.
3031.
Атеперь
можно
напрямую
считать
минимальное
время
движения:
b 1 a btg 100 2 1
Tmin
cos v1
v2
3 1,25
100
3
2 ,5
400
= 92,3 + 136,9 = 229,2 с.
31
32.
Мы перевели величины скоростей в систему СИ:v1 = 4,5 км/ч = 1,25 м/с, v2 = 9 км/ч = 2,5 м/с.
Ответ: Tmin = 229,2 с.
Прикладное использование принципа Ферма позволило избежать
процесса дифференцирования.
32
33.
3.2. Принцип наименьшего действияПусть
имеется
механическая
система,
в
которой
все
взаимодействия между ее элементами определяются законами
механики.
Введем понятие обобщенных координат qi(t), i 1, s
полностью
определяющих положение механической системы в пространстве.
33
34.
Величины qi(t),угловыми
i 1, s
могут быть декартовыми координатами,
координатами,
радиусами-векторами,
набором
координат материальных точек, составляющих систему и т. п.
Величины
dqi
q i , i 1, s
dt
Набор величин qi(t) и
обобщенные скорости.
dqi
q i ,
dt
i 1, s
определяют
состояние механической системы во все моменты времени.
34
35.
Наиболее общая формулировка закона движения механическихсистем дается так называемым
принципом наименьшего
действия (или принципом Гамильтона). Согласно этому принципу
каждая механическая система характеризуется определенной
функцией
L(q1 , q2 ,..., q s , q 1 , q 2 ,..., q s , t )
или, в краткой записи,
L(q , q , t )
причем движение системы
удовлетворяет следующему условию.
35
36.
Пусть в моменты времениt = t1 и t = t2 система занимает
определенные положения, характеризуемые двумя наборами
значений координат q(1) и q(2). Тогда между этими положениями
система движется таким образом, чтобы интеграл
t2
S
L(q, q , t )dt
(1)
t1
имел наименьшее возможное значение. Функция L называется
функцией Лагранжа данной системы, а интеграл S действием.
36
37.
В простейших случаях функция Лагранжа имеет ясный смысл изаписывается в виде
L(q, q , t ) Eк Еп ,
где Ек, Еп – кинетическая и потенциальная энергии системы
соответственно.
37
38.
Тот факт, что функция Лангранжа содержит только q и q ,, q ,...,
не более высокие производные q
но
является выражением
указанного выше факта, что механическое состояние полностью
определяется заданием координат и скоростей.
38
39.
Перейдем к выводу дифференциальных уравнений, решающихзадачу об определении минимума интеграла (1). Для упрощения
записи формул предположим сначала, что система обладает всего
одной степенью свободы, так что должна быть определена всего
одна функция q(t).
39
40.
Пусть q = q(t) есть как раз та функция, для которой действие Sимеет минимум. Это значит, что S возрастает при замене q(t) на
любую функцию вида
q(t) + q(t),
(2)
где q(t) — функция, малая во всем интервале времени от t1 до t2
(ее называют вариацией функции q(t); поскольку при t = t1, и t = t2
все сравниваемые функции (2) должны принимать одни и те же
значения q(1) и q(2), то должно быть:
q(t1) = q(t2) = 0.
(3)
40
41.
Изменение S при замене q на q + q дается разностьюt2
t2
t1
t1
L(q q, q q , t )dt L(q, q , t )dt
41
42.
Разложение этой разности по степеням qи
q
(в
подинтегральном выражении) начинается с членов первого
порядка. Необходимым условием минимальности S является
обращение в нуль совокупности этих членов; ее называют
первой вариацией (или обычно просто вариацией) интеграла.
42
43.
Такимобразом,
принцип
наименьшего
действия
можно
записать в виде
t2
S L(q , q , t )dt 0,
(4)
t1
или, произведя варьирование:
t2
L
L
q
q dt 0.
q
q
t
1
43
44.
Замечая, чтоq
d
q ,
dt
проинтегрируем второй член по
частям и получим:
t2
L
S
q
q t
1
t2
L d L
q dt 0.
q dt q
t
(5)
1
44
45.
Но в силу условий (3) первый член в этом выражении исчезает.Остается интеграл, который должен быть равен нулю при
произвольных значениях q. Это возможно только в том случае,
если подинтегральное выражение тождественно обращается в
нуль. Таким образом, мы получаем уравнение
d L L
0.
dt q q
45
46.
Приналичии
нескольких
степеней
свободы
в
принципе
наименьшего действия должны независимо варьироваться s
различных функций qi(t). Очевидно, что мы получим тогда s
уравнений вида
d L L
0
dt qi qi
( i 1,2,..., s ).
(6)
46
47.
Это искомые дифференциальные уравнения; они называются вмеханике уравнениями Лагранжа. Если функция Лагранжа
данной механической системы известна, то уравнения (6)
устанавливают
связь
между
ускорениями,
скоростями
и
координатами, т. е. представляют собой уравнения движении
системы.
47
48.
С математической точки зрения уравнения (6) составляютсистему s уравнений второго порядка для s неизвестных функций
qi(t). Общее решение такой системы содержит 2s произвольных
постоянных. Для их определения и тем самым полного
определения движения механической системы необходимо знание
начальных условий, характеризующих состояние системы в
некоторый
заданный
момент
времени,
например
знание
начальных значений всех координат и скоростей.
48
49.
Третий способ получения модели системы«шарик-пружина».
Принцип Гамильтона для механической системы гласит, если
система движется по законам механики, то q(t) – стационарная
функция для действия S[q] или
d
S[q ] 0 0.
d
(1)
49
50.
Фигурирующаяв
принципе
наименьшего
действия
(1)
функция (t) – некоторая пробная функция, обращающаяся в
нуль в моменты t1, t2 и удовлетворяющая тому условию, что
q(t) + (t) возможная координата данной системы (в
остальном (t) произвольна).
Функция (t) – вариация обобщенной координаты q(t).
50
51.
Смысл принципа Гамильтона в том, что из всех априоридопускаемых траекторий (движений) системы между моментами
t1 и t2 выбирается (реализуется) движение, доставляющее
минимум функционалу действия S.
51
52.
Воспользуемся принципом Гамильтона для построения моделидвижения шарика, соединенного с пружиной. В качестве
обобщенной
координаты
системы
естественно
выбрать
обычную эйлерову координату шарика r(t). Тогда обобщенная
скорость
dr/dt = v(t) обычная скорость шарика. Функция
Лагранжа, равная L = Ек Еп, записывается через уже
найденные значения кинетической и потенциальной энергии
системы:
m(dr / dt )2
r2
L
k .
2
2
52
53.
Для величины действия получаем выражениеm dr 2 k
dr
S[r ] L r , dt r 2 dt .
2 dt
2
dt
t
t
t2
t2
1
1
Теперь в соответствии со схемой, вычислим действие на
вариациях (t) координаты r(t):
m d ( r ) 2 k
2
S[r ]
( r ) dt .
2
dt
2
t1
t2
53
54.
Последнюю формулу необходимо продифференцировать по(учитывая, что функции r, , dr / dt, d / dt от не зависят):
d
S[r ]
d
t2
2
dr 2
d 1
dr d
d
2
2
2
2
m 2
k {r 2 r } dt
d 2 dt
dt dt
dt
t1
t2
dr d d 2
m
k {r 2 } dt ,
dt dt
dt
t1
54
55.
и положить в ней = 0:t2
d
dr d
S[r ]
m
kr dt 0.
d
dt dt
0
t
1
55
56.
Правая часть этого выражения (равного нулю в согласии спринципом Гамильтона) с помощью интегрирования ее первого
члена по частям и с учетом того, что = 0 в момент t1, t2,
преобразуется к виду:
t2
d 2r
d
S[r ]
m 2 kr dt 0.
d
0
dt
t1
56
57.
Посколькупробная
функция
(t),
фигурирующая
в
формулировке принципа наименьшего действия, произвольна,
то часть выражения, стоящая под знаком интеграла в
квадратных скобках, должна быть равна нулю во все моменты
времени t1 < t < t2:
m
d 2r
dt
2
kr ,
57
58.
т. e. движение системы должно описываться уравнениемосциллятора, полученным из закона Ньютона (первый способ) и
закона сохранения энергии (второй способ). Все три подхода
оказываются эквивалентными.
58
59.
Пример 3.Показать, что уравнение горизонтального движения шарика,
соединенного
пружиной
уравнением Эйлера для
с
некоторой
точкой
О,
является
действия интеграла от разности
кинетической и потенциальной энергий.
59
60.
РешениеПеремещение шарика задает функцию r(t), где r координата в
момент времени t. Функция r(t) удовлетворяет второму закону
Ньютона: mr (t) = kr(t), так как действующая на шарик сила по
закону Гука пропорциональна (с коэффициентом k) перемещению
и направлена противоположно ему.
60
61.
Кинетическая энергия шарика определяется выражениемT
2
m r ( t ) а потенциальная
,
2
kr 2 ( t )
U
.
2
Тогда действие
интеграл от разности кинетической потенциальной энергии
имеет вид
m r 2 ( t ) kr 2 ( t )
(T U ) dt
dt ,
2
2
t0
t0
T
T
где t0, T моменты начала и окончания движения.
61
62.
Запишем уравнение Эйлера для действия. Так какm r 2 kr 2
F
,
2
2
Fr kr , Fr m r ,
d
Fr m r ,
dt
то уравнение Эйлера имеет вид
d
Fr Fr kr m r 0
dt
или
mr = kr.
62
63.
Таким образом, уравнение второго закона Ньютона этоуравнение Эйлера для действия. Иными словами, законы
природы имеют двойное описание физическое и экстремальное.
63
64.
Вывод.Сформулированные
применительно
к
какому-либо
классу
явлений вариационные принципы позволяют единообразно
строить
соответствующие
математические
модели.
Их
универсальность выражается также в том, что, используя их,
можно в определенной степени отвлекаться от конкретной
природы
процесса.
Так,
человек,
следующий
принципу
«минимального времени» и желающий попасть из точки В,
находящейся на вспаханном поле (одна скорость), в точку А,
расположенную
на
асфальте
(другая
скорость),
обязан
перемещаться не по прямой, соединяющей В и А, а по ломанной
64
траектории, сделав необходимое «преломление» на линии,
разделяющей пашню и асфальт.
65.
4. Построение моделей на основе метода аналогийВСЕ
ФИЗИЧЕСКИЕ
законам,
среди
явления
которых
подчиняются
особое
место
неким
общим
занимают
законы
сохранения, например закон сохранения полной энергии или
закон сохранения импульса замкнутой системой. Любая такая
система, предоставленная самой себе, будет стремиться к
устойчивому положению равновесия, т е. к минимуму полной
энергии. В любой такой системе будут идти необратимые
процессы, и система будет стремиться к полному беспорядку.
65
66.
Эти и другие общие закономерности в поведении различныхфизических объектов приводят к тому, что процессы
различной физической природы описываются одинаковыми
уравнениями. Ниже мы рассмотрим некоторые простейшие
физические аналогии такого типа.
66
67.
Вряде
случаев
между
различными
объектами
материального мира (и процессами, в которых они
участвуют) существует глубокая внутренняя взаимосвязь.
67
68.
Пример тому гипотеза французского физика Л. де Бройляо
том,
что
установленный
ранее
для
фотонов
корпускулярно-волновой дуализм (заключающийся в том,
что
фотоны
обладают
и
волновыми
свойствами,
и
свойствами частиц) присущ всем частицам-электронам,
протонам, атомам и т.д. Эта гипотеза составляет основу
квантовой механики.
68
69.
Слово «аналогия» в переводе с греческого языка означаетсоответствие,
сходство.
Аналогия
весьма
эффективный
эвристический инструмент познания. Применение аналогии
предполагает
различных
следующие
заданных
соответственных
действия:
объектов
элементов
в
и
построение
отношений;
аналогичных
аналогов
нахождение
предложениях;
составление предложений или задач, аналогичных данным;
проведение рассуждений по аналогии; поиск явлений и процессов
в природе, аналогичных изучаемому явлению.
69
70.
Втех
случаях,
фундаментальные
когда
мы
законы,
не
можем
которым
определить
удовлетворяет
рассматриваемый объект моделирования, для построения
математических
моделей
реального
явления
часто
используется метод аналогий.
70
71.
Пример 1.Рассмотрим раздел биологии популяции в биологическом
мире. Задача состоит в построении математической модели
динамики популяции. Для простоты возьмем динамику
популяции
(например,
зайцев)
за
счет
рождения
и
естественной смерти.
71
72.
Вспомним явления поглощения, спонтанного излучения илирадиоактивный распад. Проведем аналогию между этими
явлениями
и
динамикой
популяций,
в
частности
изменением численности зайцев. Аналогия между этими
явлениями существует, об этом свидетельствует одна из
простейших моделей популяций, называемая моделью
Мальтуса.
72
73.
В основу этой модели положено утверждение: изменениечисла популяции N(t) пропорционально его текущей
численности
N(t),
изменению
времени,
некоторому
коэффициенту рождаемости (t) > 0:
N N t dN N dt .
t
73
74.
В результате имеемdN (t )
[ (t ) (t )] N (t ).
dt
(1)
Здесь еще учтен коэффициент естественной смертности (t) 0.
74
75.
Этоуравнение
похоже
на
уравнение
поглощения,
спонтанного излучения и радиоактивного распада. Если
< , то решение имеет вид
t1
N (t ) N 0 exp [ ] dt ,
t0
где N 0 начальное количество популяции (рис. 1).
75
76.
7677.
При = численность остается постоянной, т. е. в этом случаерешением уравнения является равновесная величина N(t) = N(0).
Равновесие между рождаемостью и смертностью неустойчиво в
том смысле, что даже небольшое нарушение равенства =
приводит с течением времени ко всё большому отклонению
функции N(t) от равновесного значения N0.
77
78.
При < численность популяции убывает и стремится к нулюпри t , а при > растет по некоторому экспоненциальному
закону, обращаясь в бесконечность при
t .
Последнее обстоятельство и послужило основанием для опасений
Мальтуса о грядущем перенаселении Земли.
78
79.
После построения простейшей модели можно использоватьиерархический подход к построению моделей (от простого к
сложному).
79
80.
Рассмотрим задачу изменения популяции за счет рождения иестественной смерти данной популяции и учтем встречи членов
популяции. Учет встреч можно описать произведением N(t)N(t).
Тогда получаем вторую модель популяционной динамики:
dN (t )
[ (t ) (t )] N (t ) (t ) N 2 ,
dt
N t 0 N 0 .
(2)
80
81.
Это уравнение впервые было предложено в 1845 г. П.Ферхюльстом
для
описания
называется
логистическим
биологических
уравнением.
популяций
и
(t)
Здесь
коэффициент, описывающий убыль популяции за счет встреч
членов популяции, борющихся между собой за пищу и жизненное
пространство.
81
82.
Рассмотрим теперь более сложную модель «хищники и жертвы»,развивающиеся на одной территории. Жертвы-вегетарианцы,
например
зайцы,
развиваются
в
условиях
существования
ограничений на территорию, ограничений в кормовой базе, а
также имеют врагов-хищников. Хищники живут за счет жертв.
Для простоты возьмем только один вид хищников волка.
82
83.
Тогдаматематическая
модель,
описывающая
процесс
развития численности этих популяций, примет вид
dN 1 ( t )
[ 1 ( t ) 1 ( t )]N 1 1 ( t ) N 12 1 N 1 N 2 ,
dt
(3)
dN 2 ( t )
[ 2 ( t ) 2 ( t )]N 2 2 ( t ) N 22 2 N 2 N 1 .
dt
83
84.
Здесь N 1 число зайцев; N 2 число волков; 1(t), 2(t)коэффициенты рождаемости;
1(t), 2(t) коэффициенты естественной смерти;
1(t), 2(t) коэффициенты, описывающие убыль популяции
за счет встреч членов популяции, борющихся между собой за
пищу и жизненное пространство;
84
85.
1(t), 2(t) коэффициенты, описывающие изменение численностипопуляции за счет встреч волков и зайцев;
N 1 t 0 N 10
численность
зайцев в начальный момент
N 2 t 0 N 20
численность
волков
времени;
в
начальный
момент
времени.
85
86.
Уравнения вида (2) (3) и их модификации являютсяуниверсальными моделями для рассмотрения динамики
любого вида популяций, в том числе человека и его
окружения, и являются базовыми для описаний явлений
этногенеза, социогенеза и других подобных явлений.
86
87.
Применение аналогий основано на одном из важнейшихсвойств
моделей
приложимости
к
–
их
универсальности,
объектам
принципиально
т.
е.
их
различной
природы.
87
88.
Пример 2.Маленький стальной шарик массой М падает в воду под
углом к нормали со скоростью v0 (рис. 2). На шарик в воде
действует сила сопротивления, пропорциональная скорости
( F v ).
Найдите
зависимость
горизонтальной
и
вертикальной составляющих скорости шарика от времени.
Определите также установившуюся скорость шарика.
88
89.
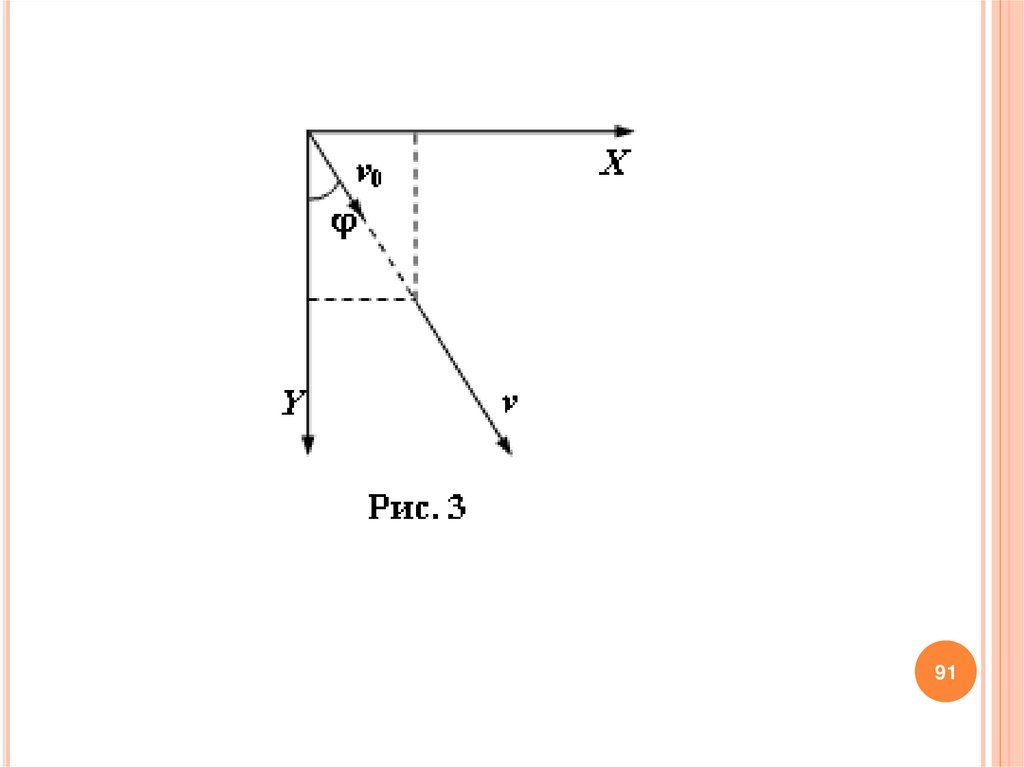
8990.
РешениеБудем
рассматривать
движение
шарика
в
системе
координат, изображенной на рисунке 3.
Второй закон Ньютона:
dv
M
v Mg .
dt
90
91.
9192.
Уравнение движения шарика вдоль оси X запишем в видеdv x
vx .
dt
M
92
93.
Характерной особенностью является то, что скоростьизменения величины vx пропорциональна самой величине, а
знак «минус» означает, что vx убывает.
dv x
dt
vx
M
v x Ae
t
M .
93
94.
Константу А находим из начальных условий: при t = 0v x 0 v0 sin A.
Зависимость
горизонтальной
составляющей
скорости
шарика от времени будет иметь вид
v x ( t ) v0 sin e
t
M .
94
95.
Это означает, что составляющая скорости шарика вдоль осиX экспоненциально убывает и при t стремится к нулю.
Формально горизонтальная скорость станет нулевой через
бесконечное время, однако реально это произойдет через
конечное время.
95
96.
Такие процессы принято характеризовать так называемойпостоянной времени (временем релаксации) . В данном
случае это время, за которое скорость упадет в е раз, оно
равно =М/ .
96
97.
Теперь запишем уравнение движения шарика вдоль оси Y:M
vy
g .
dt
M
dv y
97
98.
Mg.
Введем новую переменную u v y
du dv y
.
dt
dt
98
99.
Тогда уравнение движения будет иметь видdu
u,
dt
m
а его решение
u( t ) Be
t
M .
99
100.
Константу В найдем из начальных условий: при t = 0u v0 cos
M
g B,
и, следовательно,
M
M
vy
g v0 cos
g e
t
M .
100
101.
Отсюдаv y ( t ) v0 cos e
t
t
M M g 1 e M .
101
102.
При t вертикальная составляющая скорости шарикастремится к постоянному значению vy( ) = Мg/ с той же
самой постоянной времени = М/ .
102
103.
Итак, установившаяся скорость шарика будет направленавертикально вниз и равна Мg/ , а произойдет это примерно
через время, равное .
Графики зависимости vx(t) и v y(t) показаны на рисунке 4.
103
104.
104105.
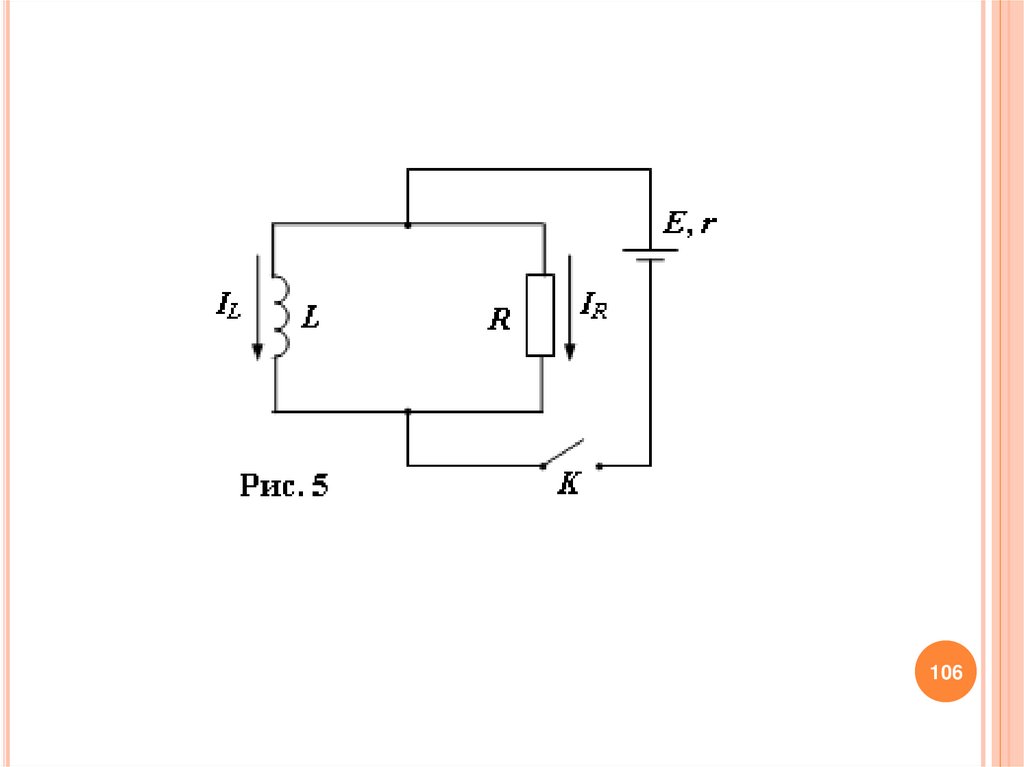
Пример 3.Параллельно соединенные катушка индуктивностью L и
резистор сопротивлением R подключены через ключ K к
батарее с ЭДС E и внутренним сопротивлением r (рис. 5). В
начальный момент времени ключ разомкнут и тока в цепи
нет. Найдите зависимость от времени токов через резистор
и
катушку
после
замыкания
ключа.
Омическим
сопротивлением катушки пренебречь.
105
106.
106107.
Пусть в произвольный момент времени после замыканияключа K через резистор течет ток I R (t), а через катушку
ток I L(t) (рис. 5). Очевидно, что ток батареи равен
суммарному току I R (t) + I L(t)
107
108.
Выберем два замкнутых контура и запишем для каждого изних закон Ома (точнее, второе правило Кирхгофа).
Для контура, охватывающего батарею и резистор, имеем
E = I R (t)R + (I R (t) + I L(t))r.
E I L ( t )r
I R (t )
.
R r
108
109.
Аналогично для контура, содержащего катушку и резистор:dI L ( t )
L
I R ( t ) R.
dt
Подставляя сюда выражение для тока I R из (1), найдем
dI L
rR
ER
rR
E
IL
I L .
dt
L( R r )
L( R r )
L( R r )
r
109
110.
Введем новую переменную x = I L E/r и получимdx dI L
dt
dt
dx
rR
x.
dt
L( R r )
110
111.
Это уже знакомое нам уравнение, его решение имеет видx(t) = x0e t,
где
rR
,
L( R r )
а х0 константа, которую найдем из
начальных условий: при t = 0 (сразу после замыкания
ключа) I L = 0, следовательно, х0 = E/r .
111
112.
Поэтому зависимость тока I L от времени будет такой:rRt
E
L( R r )
IL 1 e
,
r
т.е. ток через катушку нарастает по экспоненциальному
закону с постоянной времени = L(R + r)/(Rr). А для тока
I R из самого первого уравнения найдем
E
IR
e
R r
rRt
L( R r )
.
112
113.
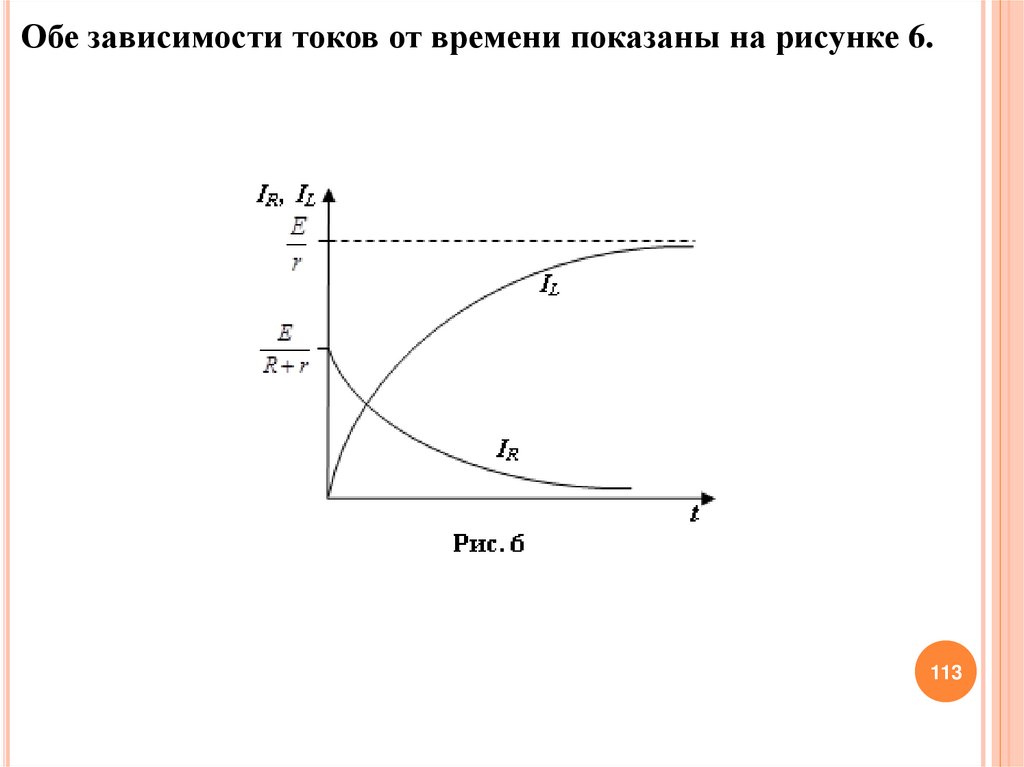
Обе зависимости токов от времени показаны на рисунке 6.113
114.
Пример 4В некоторый момент времени счетчик радиоактивного
излучения,
расположенный
вблизи
препарата
18 F,
зафиксировал 100 отсчетов в секунду. Через время t = 20
мин показание уменьшилось до 87 отсчетов в секунду.
Определите период полураспада 18F.
114
115.
Прежде всего найдем закон радиоактивного распада, т.е.зависимость
числа
нераспавшихся
атомов
N
радиоактивного изотопа 18F oт времени t. Радиоактивный
распад это свойство самого атомного ядра и зависит
только от его внутреннего состояния, поэтому для каждого
атомного ядра вероятность радиоактивного распада в
единицу
величиной.
времени
является
некоторой
постоянной
115
116.
Обозначим вероятность радиоактивного распада ядра атома18F в единицу времени через . Число актов радиоактивного
распада
dN
за
время
dt
определяется
количеством
радиоактивных ядер N(t) в данный момент времени t:
dN Ndt ,
или
dN
N .
dt
116
117.
Опять мы имеем уравнение, описывающее процесс, вкотором
скорость
изменения
со
временем
некоторой
величины (числа радиоактивных ядер) пропорциональна
этой величине в данный момент времени.
117
118.
Решение этого уравнения имеет видN = N 0 e t ,
где N 0 число радиоактивных ядер в начальный момент
времени (t = 0). Это и есть закон радиоактивного распада.
Постоянная времени данного процесса (или средняя
продолжительность жизни) равна = 1 / .
118
119.
На практике принято характеризовать продолжительностьжизни радиоактивного изотопа периодом полураспада Т,
т.е. временем, в течение которого распадается половина
начального
количества
атомов.
Используя
закон
радиоактивного распада, можно записать
N (t ) 1
e T ,
N0
2
откуда
T
ln 2
.
119
120.
Перейдемтеперь
к
решению
нашей
задачи.
Первое
показание счетчика примем за начало отсчета (t = 0). Тогда
первое показание есть
dN
N 0 ,
dt t 0
120
121.
где коэффициент учитывает долю распадов, которуюрегистрирует счетчик (геометрический фактор). Второе
показание счетчика есть
dN
N 0e t .
dt t t
121
122.
Отношение первого показания ко второму (т. е. 100/87)равно
= e t.
Прологарифмировав обе части этого равенства, получим
ln
.
t
122
123.
Следовательно, период полураспадаT
ln 2 ln 2
t 1,55 ч.
ln
123
124.
Разобранные нами физические процессы, несмотря на ихсущественные различия по своей природе, описываются
дифференциальными уравнениями одного вида. Все эти
процессы
имеют
экспоненциальную
временную
зависимость со своей постоянной времени.
124
125.
Спасибо за внимание!125


















































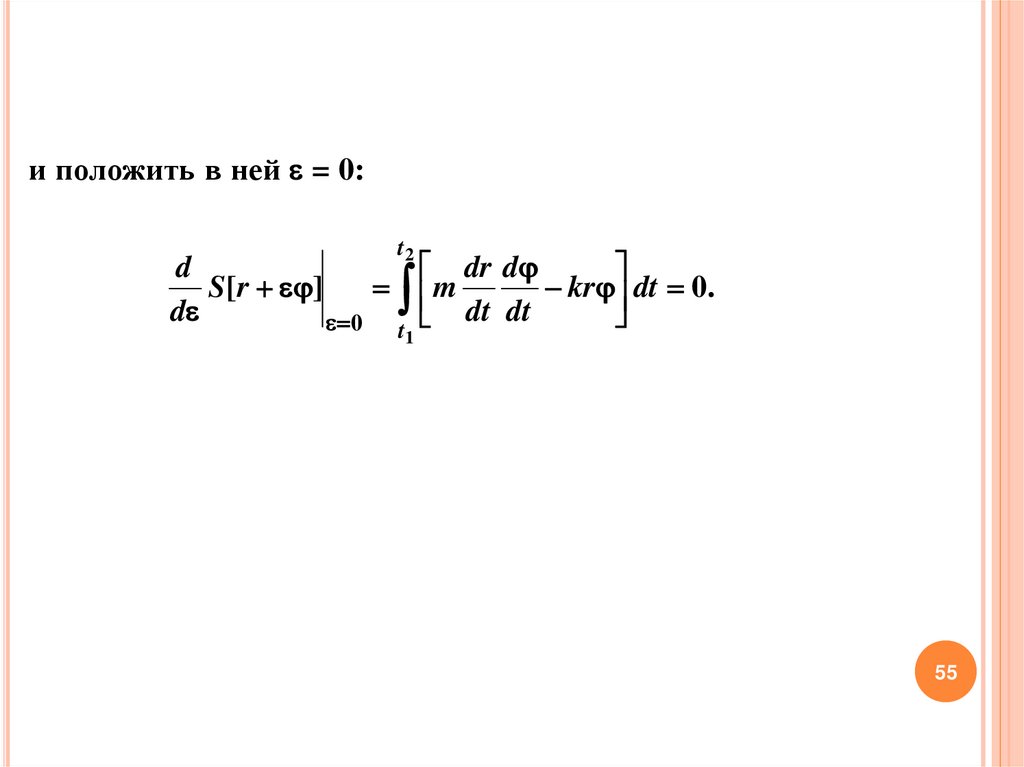
































































 physics
physics








