тема теория групп_мой

1. Проверочная работа

1. Что такое зона в кристалле?
2. Определить условие принадлежности плоскости зоне.
3. В чем состоит закон Вейса?
4. Как построить проекцию с произвольной осью?
5. Какой инструмент используют для построения
гномостереографических проекций граней кристалла?

2. Основы теории групп

3. Теория групп: два примера групп

1) Множество целых чисел.
Положим что Z – бесконечный набор целых чисел: {0, ±1, ±2, ±3, …}.
Сумма двух любых чисел также дает целое число: z3 = z1+z2.
Сложение любого числа с 0 дает то же число: z+0=z.
Для каждого z существует –z, сумма которых дает 0: z+(-z)=0.
Соотношение z1+z2 = z2+z1 всегда выполняется.

4. Теория групп: два примера групп

2) Симметрия G квадрата.
Множество G состоит из 8 элементов g1, g2, … g8:
вращение по часовой стрелке вокруг оси 4 порядка на 90°,
вокруг оси 2 порядка на 180°, а также в обратную сторону 4-1
(или 43 на 270°), отражения mx, my, m+, m-, а также ось 1.
Действие каждого элемента симметрии, или любой
совокупности 2 элементов воспроизводит квадрат.
Совокупность любого элемента g с 1 эквивалентно g.
Для любого g существует g-1 , совокупность которых дает 1.
В отличие от Z, последовательность действий для G имеет
значение: 4 + mx = m- , mx + 4 = m+

5. Теория групп: два примера групп

Общее свойство двух рассмотренных групп:
Если мы возьмем три элемента z1, z2, z3 или g1, g2, g3, не важно, как эти
элементы компонуются:
(z1+z2)+z3 = z4+z3=z6 или z1+(z2+z3) = z1+z5=z6 - результат тот же.
Таким же образом:
(g1 ◦ g2) ◦ g3 = g4 ◦ g3 = g6 = g1 ◦ (g2 ◦ g3) = g1 ◦ g5 = g6
(◦ - последовательное выполнение)
Т.о. обе эти группы ассоциативны относительно выбора компоновки
элементов.
У множеств Z и G общие свойства, такие же свойства могут иметь и
другие наборы элементов. Все наборы элементов, имеющих
одинаковые свойства объединяют в группу.

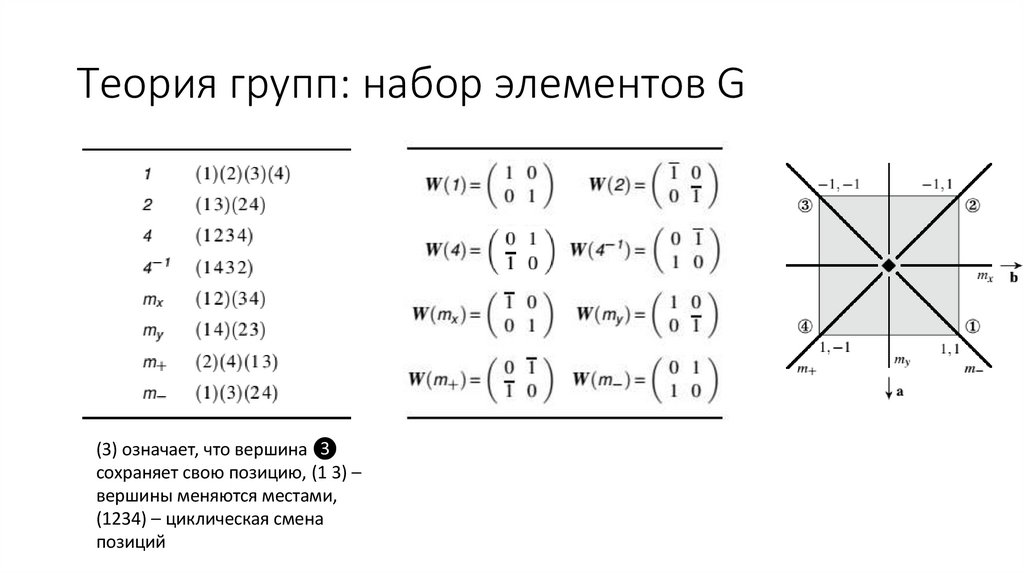
6. Теория групп: набор элементов G

Выбор последовательностей элементов симметрии для
выполнения операций проще проводить аналитически.
Например: вращение куба по [111] на 120° , а затем по [010] на 270
°-?
Инструменты: перестановка вершин ❶❷❸❹ и матрицы.
Одна перестановка и одна матрица отвечают за одну операцию,
перестановка и перемножение соответственно описывают
последовательность операций.

7. Теория групп: набор элементов G

(3) означает, что вершина ❸
сохраняет свою позицию, (1 3) –
вершины меняются местами,
(1234) – циклическая смена
позиций

8. Теория групп: набор элементов G

Первая операция
Сначала 4, потом mx
Сначала mx, потом 4
В
т
о
р
а
я
Получаем (1)(3)(24) или m-
Получаем (2)(4)(13) или m+

9. Основы теории групп: аксиомы

1) Замыкание: группа — это множество G элементов gi, для которых
имеет место закон композиции. Композиция любых двух элементов gi◦gk
дает в точности один элемент gj∈G:
gj = gi◦gk
2) Компоновка элементов ассоциативна.
3) Один из элементов группы является элементом идентичности, g1 =
е и имеет свойство:
еgi = giе для всех gj∈G
4) Каждый gj∈G имеет обратный элемент х∈G, такой что
соблюдается условие xg = gx = e. Обычно обозначается g-1. Элемент
обратный к g - g-1 . Если g ≠ g-1, то есть пара g и g-1.

10. Основы теории групп: термины

• Количество элементов в группе называется порядком группы
• Если g∈G, то gg=g2, ggg=g3 и т.д. тоже элементы G. Если G конечного
порядка, то есть такое минимальное k, что gk=e. k называется
порядком элемента g.
• Если для всех пар элементов gi, gk ∈ G выполняется gigk = gkgi, то G
называется коммутативной или абелевой группой.
• Произвольное подмножество A = {a1, a2, a3, ...} ⊆ G называется
комплексом из G. К комплексу обычно не применимы аксиомы групп.
gi A относится к множеству {gia1, gia2, gia3, ...} произведений gi с
элементами A; Agi обозначает множество {a1gi,a2gi,a3gi,...}. Если B = {b1,
b2, b3,...} ⊆ G также является комплексом из G , то AB — множество
всех произведений ai bk, AB = {a1 b1, a2 b1, a3 b1, ..., a1 b2, ..., ai bk,...}; ВА –
это совокупность всех произведений bi ak.

11. Основы теории групп: термины

• Комплекс H ⊆ G, удовлетворяющий групповым аксиомам, называется
подгруппой, записывается как H ≤ G. Если G содержит элементы, не
входящие в H, т. е. если H (как множество) меньше G, то H называется
собственной подгруппой G, H < G. По аналогии G ≥ H называется
супергруппой H и G > H собственной супергруппой группы H. G ≤ G как
подгруппа самой себя и единичный элемент e (который всегда
образует группу как таковой) являются тривиальными подгруппами G .
Если мы рассматриваем e как группу, мы пишем {e}.
• H < G называется максимальной подгруппой группы G, если не
существует промежуточной группы Z, для которой выполняется H < Z <
G. Если H является максимальной подгруппой G , то G > H называется
минимальной супергруппой группы H.

12. Основы теории групп: термины

• Комплекс элементов g1, g2,... называется множеством генераторов
группы G, если G (т. е. все элементы G ) могут быть порождены
повторяющимися сочетаниями генераторов.
• Например, группа симметрии квадрата, среди прочего, может быть получена из
{4, mx} или {mx, m+} или {1, 4−1, mx, my} или {4, 2, 4−1, m-, m+}.
• Группа G называется циклической, если она может быть порождена
одним из своих элементов a ∈ G (a и a−1 в случае бесконечных групп).
Для конечных циклических групп порядок a является порядком
группы.

13. Основы теории групп: термины

• Группу малого порядка можно наглядно представить как таблицу группового
умножения.
• Группы, которые имеют одну и ту же таблицу умножения групп или одну и ту же
таблицу после перестановки строк и столбцов называются изоморфными. Иными
словами две группы G и G’ изоморфны, G ∼ = G’, если
• существует обратимое преобразование G в G’, gi ↔g’i ;
• произведение g’i g’k элементов gi и gk равно элементу (gi gk)’ произведения gi gk для каждой
пары gi, gk ∈ G . Более формально: g’i g’k = (gi gk)’.
Все группы можно разделить по типу (классу) изоморфизма изоморфных групп. Такой
класс также называется абстрактной группой; сами группы являются реализациями
абстрактной группы.
В теоретико-групповом смысле нет различия между различными реализациями
одной и той же абстрактной группы. Это позволяет заменить группу преобразований
соответствующей группой матриц (или перестановок) и, таким образом, становится
возможным обрабатывать геометрическую группу с помощью аналитических
инструментов.

14. Основы теории групп: разложение групп на смежные классы

Пусть G — группа и H < G — подгруппа. Разложение группы G относительно H
определяется следующим образом:
(1) Подгруппа H является первым смежным классом.
(2) Если g2 ∈ G , но g2 не ∈ H , то комплекс g2 H является вторым смежным
классом (левым смежным классом, так как g2 находится в левой части). Ни один
элемент из g2 H не является элементом H, и все элементы g2 H различны.
Следовательно, смежные классы H и g2 H имеют |H| элементов каждый.
(3) Если g3 ∈ G, но g3 не ∈ H и g3 не ∈ g2H, то комплекс g3 H является третьим
(слева) смежным классом. Все элементы g3 H различны, и ни один элемент g3 H не
появляется в H или g2 H ; все элементы новые.
(4) Процедуру продолжают до тех пор, пока не останется ни одного элемента
G. В результате G разложена на левые смежные классы по H. Таким же образом G
можно разложить на правые смежные классы H, H g2,....
(5) Количество правых и левых смежных классов одинаково; оно называется
индексом H в G.

15. Основы теории групп: разложение групп на смежные классы

Таким образом, каждый элемент G появляется точно в одном смежном классе
и каждый смежный класс содержит |H| элементов. Только первый смежный
класс является группой, т.к. только он содержит элемент идентичности. Из hjH
= H следует, что каждый элемент gihi класса giH может быть использован для
генерации смежного класса.
Учитывая, что hi ∈ H и n = |H|, элементы gi ∈ G распределяются по левым
смежным классам следующим образом:
1-й
2-й
3-й
i-й

16. Основы теории групп: разложение групп на смежные классы

G = {1, 2, 4, 4−1, mx, my, m+, m-}
Разложение относительно Н = {1, 2}
1й смежный класс
2й смежный класс
3й смежный класс
4й смежный класс
Левые
1 ◦ Н = {1, 2}
4 ◦ Н = {4, 4−1}
mx ◦ Н = {mx, my}
m+ ◦ Н = {m+, m-}
Правые
Н ◦ 1 = {1, 2}
Н ◦ 4 = {4, 4−1}
Н ◦ mx = {mx, my}
Н ◦ m+ = {m+, m-}
Получаем 4 смежных класса, индекс 4. Правые и левые смежные классы одинаковые
Разложение относительно Н = {1, mx}
1й смежный класс
2й смежный класс
3й смежный класс
4й смежный класс
Левые
1 ◦ Н = {1, mx}
4 ◦ Н = {4, m-}
2 ◦ Н = {2, my}
4−1 ◦ Н = {4−1, m+}
Правые
Н ◦ 1 = {1, mx}
Н ◦ 4 = {4, m+}
Н ◦ 2 = {2, my}
Н ◦ 4−1 = {4−1, m-}
Правые и левые смежные классы разные

17. Основы теории групп: разложение групп на смежные классы

Теорема Лагранжа: Если G – конечная группа и H<G, то порядок |H|
подгруппы Н – это делитель порядка |G| группы G.
Количество смежных классов i, в каждом их которых |H| элементов и каждый
элемент из G появляется лишь однажды определяется как: i = |G| / |H|.
Уравнение справедливо только для конечных групп.
Т.о. группа квадрата может иметь подгруппы порядка 1, 2, 4, 8.
Это бессмысленно для бесконечной группы, однако, можно разделить
бесконечную группу пополам:

18. Основы теории групп: классы сопряженности

Элементы gi и gj, gi, gj ∈ G называются сопряженными в G, если
существует такой элемент gm ∈ G, что выполняется условие
gj = gm-1gigm. Набор элементов, сопряженных с gi, когда gm проходит
по всем элементам G называется классом сопряженности gi.
Иными словами gi может трансформироваться в gj элементом gm.
Элементов, трансформирующих gi в gj может быть несколько.
Относительно групп симметрии: две операции симметрии группы
G сопряжены, если они трансформируются одна в другую при
действии какой-либо третьей операции из той же группы G.

19. Основы теории групп: классы сопряженности

В группе симметрии квадрата поворот 4 трансформирует m+ в m- и
наоборот. Та же трансформация может быть достигнута
действиями 4−1, mx, my, тогда как другие операции оставляют m+ в
m- неизменными. Отражения m+ и m- являются сопряженными и
вместе формируют класс сопряженности.

20. Основы теории групп: свойства сопряженности

• Каждый элемент G принадлежит только к одному классу сопряженности.
• Количество элементов в классе сопряженности различно, однако оно
является делителем G.
• Если gi ∈ G и если выполняется условие gi = gm-1gigm для всех gm ∈ G, то gi
называется самосопряженным. Поскольку это условие эквивалентно gi gm=
gm gi , то можно сказать, что gi взаимозаменяем со всеми элементами G’.
• Для абелевых групп из условия gi = gm-1gigm следует, что каждый элемент
самосопряжен и, таким образом, сам образует класс сопряженности. Точно
так же как элемент идентичности e ∈ G любой группы сам по себе образует
класс.
• Элементы одного и того же класса сопряженности имеют одинаковый
порядок.

21. Основы теории групп: подгруппы сопряженности

Подгруппы H, H’ < G называют подгруппами сопряженности группы G, если
существует такой элемент gm ∈ G, при котором выполняется условие Н’ = gm1Hg
m. Множество подгрупп, сопряженных с H, образует класс сопряженности,
когда gm проходит через все элементы G.
Подгруппы сопряженности изоморфны и таким образом имеют один и тот
же порядок:
Множество всех подгрупп группы G разбивается на классы сопряженности
подгрупп. Подгруппы одного и того же класса сопряженности изоморфны.
Число подгрупп в таком классе есть делитель порядка |G|. Каждая подгруппа
группы G принадлежит ровно одному классу сопряженности. Разные классы
сопряженности могут содержать разное количество подгрупп.
{1, m+} и {1, m-} – сопряженные подгруппы G, т.к. 4−1 {1, m+} 4 = {1, m-}. Эти две
группы из одного класса сопряженности. {1, mx} и {1, my} – из другого, т.к. 4−1
{1, mx} 4 = {1, my}.

22. Основы теории групп: подгруппы сопряженности

Пусть H < G. Если gm-1Hgm = Н выполняется для всех gm ∈ G, то H
называемой нормальной подгруппой группы G, обозначаемой H G
(инвариантная подгруппа или самосопряженная подгруппа).
gm-1Hgm = Н эквивалентно Hgm = gmН. Следовательно, разложение
смежных классов нормальной подгруппы дает одинаковые правые и
левые смежные классы. Нормальная подгруппа также может быть
определена этим свойством. Отсюда следует самосопряженность в G .
{1, 2} G, но это не является справедливым для {1, mx}.
Каждая группа G имеет две тривиальные нормальные подгруппы:
элемент идентичности {e} и себя (G ). Все остальные нормальные
подгруппы называются собственными нормальными подгруппами.

23. Основы теории групп: факторные группы

Классы смежности группы G по отношению к нормальной подгруппе N
G сами по себе образуют группу, которая называется факторной группой
F = G/N. Классы смежности считаются новыми элементами группы. Они
связаны комплексным умножением.
Рассмотрим точечную группу 3m, которая состоит из: 1, 3, 3-1, m1, m2, m3.
Ее подгруппа 3 состоит из элементов: 1, 3, 3-1, которая также является
первым смежным классом разложения смежного класса 3m по
отношению к 3. Левый и правый смежные классы совпадают; поэтому
подгруппа 3 является нормальной подгруппой. Факторная группа 3m/3
состоит из двух элементов {1, 3, 3−1} и {m1, m2, m3}. Повороты теперь
считаются одним элементом группы, а отражения в общем образуют
другой элемент. Нормальная подгруппа в этом случае {1, 3, 3−1} является
новым элементом идентичности факторной группы.

24. Основы теории групп: факторные группы

Нормальная подгруппа N группы G – элемент идентичности факторной
группы F = G/N. Элемент, обратный gi N - gi-1N.
Пусть G – группа квадрата, а N – нормальная подгруппа {1, 2} G.
Таблица перемножения факторных групп F будет выглядеть как:
Элемент идентичности - {1, 2}. Таблица равна таблице перемножения
точечной группы mm2, значит эта факторная группа изоморфна mm2.

25. Основы теории групп: гомоморфизм

Преобразование G → G’ называется гомоморфным, если для всех
пар элементов gi , gk ∈ G, которые трансформируются, справедлив
переход gi → g’i , gk → g’k и соблюдается условие (gi gk )’= g’i g’k .
В случае изоморфизма существует только один
трансформированный элемент из начального, поэтому
трансформация обратима, тогда как в случае гомоморфизма нет
ограничений на то, какое количество элементов G
трансформируется в один элемент G’. Таким образом,
гомоморфизм – частный случай изоморфизма.

26. Основы теории групп: пример гомоморфизма

Пусть G = {W1, …., W8} – группа матриц квадрата, их детерминанты =
+/-1. Определение детерминанта является гомоморфным
преобразованием группы матриц G в группу чисел G’ = {-1, 1} .
det(Wi Wk) = det(Wi )det(Wk).
Преобразование необратимое.

27. Основы теории групп: гомоморфизм в кристаллографии

Пусть G → G’ гомоморфное преобразование. Тогда нормальная
подгруппа K G трансформируется в элемент идентичности e’, а
элемент идентичности G’ и смежные классы giK – в оставшиеся
элементы gi’∈G’. Таким образом, факторная группа G/K изоморфна
G’. Нормальная подгруппа К называется ядром гомоморфизма.
Гомоморфизм является изоморфизмом, если K={e}, т.е. G’
изоморфна G.
Если G – пространственная группа кристалла, К – группа всех
трансляций, G’ – точечная группа этого кристалла, тогда точечная
группа изоморфна факторной группе пространственной группы
относительно группы ее трансляций.

28. Действие группы на множество

Пусть G группа элементов e, g2, …., gi, … и пусть М – множество
элементов m1, m2, …., mi ,…
Группа G действует на множество М если:
1) mi = gim – это уникальный элемент mi∈М для каждого gi∈G и
каждого m∈М.
2) em = m выполняется для каждого m∈М и элемент идентичности
е∈G.
3) gk(gim) = (gkgi)m справедливо для каждой пары gk gi ∈ G и
каждого m∈М.

29. Действие группы на множество

Множество элементов mi∈М, полученных mi = gim, где gi - все
элементы группы G называется G-орбитой m или орбитой Gm.
Если G – пространственная группа и m – атом из множества атомов
М, то орбита Gm – это множество всех симметричноэквивалентных атомов m кристалла.
Или
Отображение точки Хо операциями симметрии пространственной
группы дает бесконечное множество точек, которое называется Gорбитой Хо или GXo.

30. Действие группы на множество: определения

Множество gi∈G, для которого выполняется m = gim, называется
стабилизатором S для m в G.
В кристалле стабилизатор m в G — это набор всех операций симметрии
пространственной группы G, которые отображают атом m в самого себя.
Стабилизатором является не что иное, как симметрия точки Хо, в которой
находится атом.
Стабилизатор при этом – это подгруппа G.
Если |G| – порядок конечной группы G и |S| порядок стабилизатора S
элемента m∈M, то L = |G|/|S| это длина орбиты Gm.
Иными словами, длина - это количество симметрично-эквивалентных точек.
Пример: Порядок группы G симметрии квадрата - |G|=8. Вершина m=1
трансформируется сама в себя с помощью операций 1 и m_; стабилизатор
этой группы S={1, m_}, его порядок |S|=2. Для орбиты Gm L = 8/2 = 4.
Получается, что есть 4 точки, симметрично эквивалентных 1.

31. Проверочная работа

1. Перечислить 4 групповые аксиомы.
2. Что называют порядком группы?
3. В каком случае подмножество, выделенное из группы, можно
называть подгруппой?
4. Какую группу называют циклической?
5. Что называют генератором группы?

32. Точечные группы

33. Обозначение точечных групп по Шенфлису

Сn— группы с одной поворотной осью
Sn — группы с зеркально-поворотной осью
Сnv— группы с поворотной осью n-го порядка и параллельной ей плоскостью
Сnh— группы с поворотной осью n-го порядка с перпендикулярной ей
плоскостью
Dn— группы, в которых помимо оси n-го порядка имеются 2
перпендикулярные ей оси 2 порядка.
Dnh — группы, в которых помимо оси n-го порядка имеются перпендикулярные
ей оси 2 порядка и плоскости (оси лежат в плоскостях).
Dnd— группы, в которых помимо оси n-го порядка имеются перпендикулярные
ей оси 2 порядка и плоскости (оси 2 прядка не лежат в плоскостях).

34. Обозначение точечных групп по Шенфлису

35. Матричная запись поворота на 60 и 120 градусов c использованием косоугольной системы координат

Зеркальные повороты
Зеркальный поворот – это сочетание поворота вокруг оси и последующего отражения
в плоскости, перпендикулярной поворотной оси.
m+L1 1ሶ = m
1
m+L2 2ሶ = 0
0
0 0
−1 0 0 −1 0
0
1 0 * 0 −1 0 = 0 −1 0 = ഥ1
0 −1
0
0 1
0
0 −1
0
1
0
m+L3 3ሶ = −1 −1 0 , 3ሶ 2 = 32, 3ሶ 3 = m, 3ሶ 4 = 31, 3ሶ 5 = 3ሶ -1, 3ሶ 6 = e
0
0 −1
Зеркальный поворот на 120 градусов является генератором циклической группы 6-го
порядка со следующим групповым множеством:
G = {3ሶ 1, 32, m, 31, 3ሶ -1, e}

36. Зеркальные повороты

1 0 0
0 1 0
0 1 0
41ሶ = 0 1 0 * −1 0 0 = −1 0 0
0 0 −1
0 0 1
0 0 −1
Зеркальный поворот на 90 градусов генерирует циклическую группу 4
порядка:
G = {4ሶ 1, 21, 4ሶ -1, e}
1 0 0
1 1 0
1 1 0
61ሶ = 0 1 0 * −1 0 0 = −1 0 0
0 0 −1
0 0 1
0 0 −1
Зеркальный поворот на 60 градусов генерирует циклическую группу 6
порядка:
G = {6ሶ 1, 31, ഥ1, 32, 6ሶ 5, e}

37. Зеркальные повороты

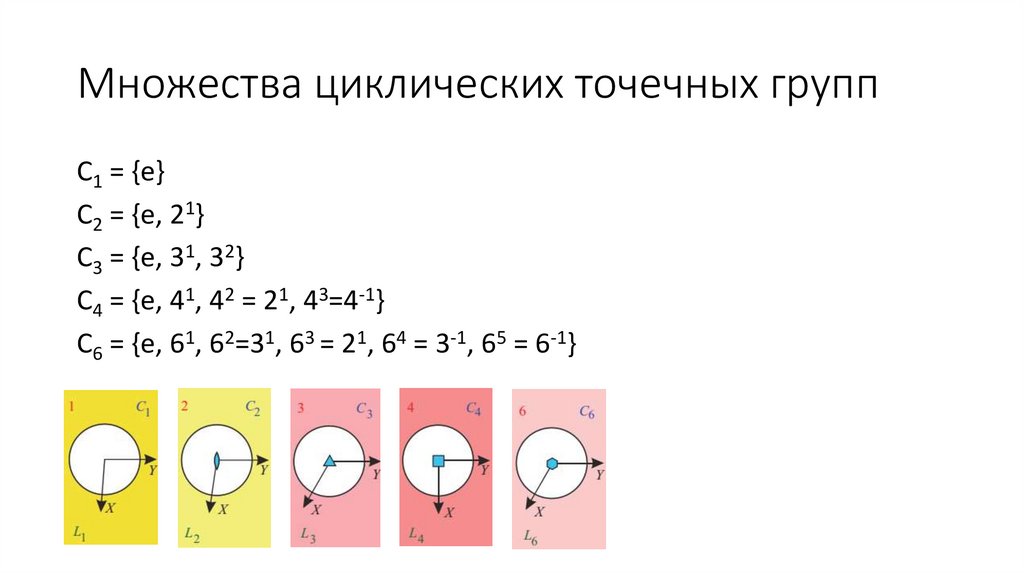
Множества циклических точечных групп
С1 = {e}
C2 = {e, 21}
C3 = {e, 31, 32}
C4 = {e, 41, 42 = 21, 43=4-1}
C6 = {e, 61, 62=31, 63 = 21, 64 = 3-1, 65 = 6-1}

38. Множества циклических точечных групп

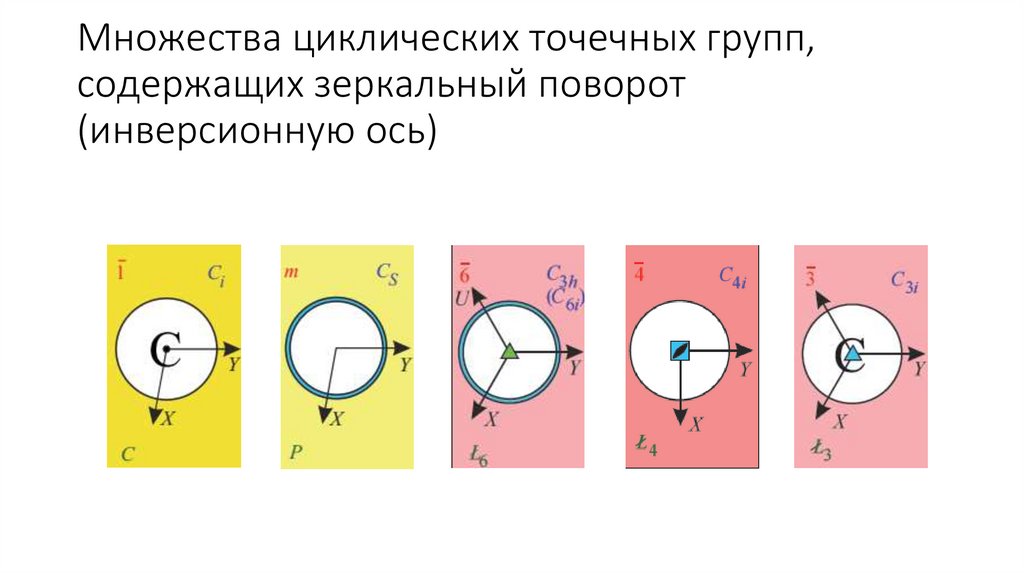
Множества циклических точечных групп,
содержащих зеркальный поворот
S1 = {e, 1}ሶ = {e, m}, имеет особое обозначение - Сs
S2 = {e, 2}ሶ = {e, ഥ1}, имеет особое обозначение - Сi
S3 = {e, 3ሶ 1, 3ሶ 2=3-1, 3ሶ 3 = m, 3ሶ 4 = 31, 3ሶ 5 = 3ሶ -1}: группа содержит
циклическую подгруппу поворотов вокруг оси
3-го порядка {e, 31, 3-1} и отражение в перпендикулярной плоскости
симметрии {e, m}, обозначение – С3h
S4 = {e, 4ሶ 1, 4ሶ 2 = 21, 4ሶ 3= 4ሶ -1}
S6 = {e, 6ሶ 1, 6ሶ 2=31, 6ሶ 3 = ഥ1, 6ሶ 4 = 32, 6ሶ 5 = 6ሶ -1}: группа имеет в качестве
подгрупп С3 и Сi, поэтому ее часто обозначают символом С3i

39. Множества циклических точечных групп, содержащих зеркальный поворот

Множества циклических точечных групп,
содержащих инверсионную ось
ഥ1 = ഥ1 (Сi)
ഥ21 = m (Сs)
−1 0
0
0
1 0 1 −1 0
ഥ31 = 0 −1 0 * −1 −1 0 = 1 1
0 = 65ሶ
0
0 −1
0
0 1 0 0 −1
G = { ഥ31= 6ሶ 5, ഥ32 = 32, ഥ33 = 1ത , ഥ34 =31, ഥ35 =6ሶ 1, e} – то же, что S6.
ഥ41– то же, что S4
ഥ61– то же, что S3

40. Множества циклических точечных групп, содержащих инверсионную ось

Множества циклических точечных групп,
содержащих зеркальный поворот
(инверсионную ось)

41. Множества циклических точечных групп, содержащих зеркальный поворот (инверсионную ось)

Группы с двумя генераторами: два
отражения
Два отражения в плоскостях симметрии, пересекающихся под углом φ, дают в
произведении поворот вокруг оси симметрии с элементарным углом поворота
2φ, расположенные по линии пересечения плоскостей. Из условий,
накладываемых на порядки кристаллографических осей, следует, что углы,
под которыми могут пересекаться плоскости симметрии, могут быть равны
лишь 90°, 45°, 60° и 30° . Наряду с поворотами вокруг оси n-го порядка
присутствуют отражения в n плоскостях симметрии, параллельных оси.
Построенные таким образом группы симметрии обозначаются, по Шенфлису,
символами Cnv.
C2v = {e, m1, m2, 21} (пересечение плоскостей 90 град)
C3v = {e, m1, m2, m3, 31 , 32} (60 град)
C4v = {e, m1, m2, m3, m4, 41 , 42 =21, 43 =4-1} (45 град)
C6v = {e, m1, m2, m3, m4, m5, m6, 61 , 62 =31, 63 =21, 64 =32, 65 =6-1} (30 град)

42. Группы с двумя генераторами: два отражения

43. Группы с двумя генераторами: два отражения

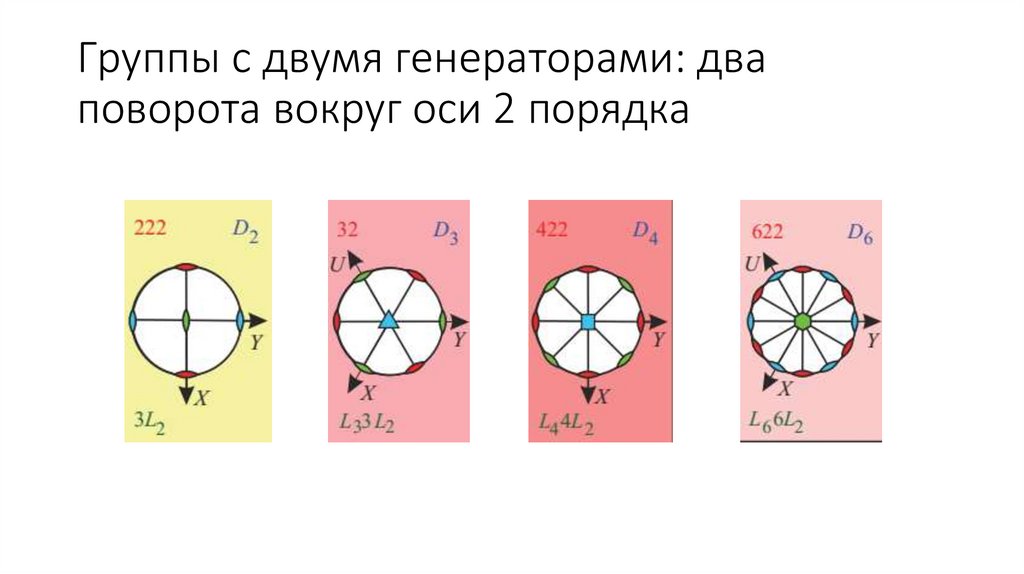
Группы с двумя генераторами: два
поворота вокруг оси 2 порядка
В результате умножения выбранных генераторов получится новая ось
симметрии с элементарным углом поворота 2φ. Углы, под которыми
могут пересекаться оси симметрии, могут быть равны лишь 90°, 45°, 60°
и 30°. Такие группы характеризуются осью n-го порядка и n осями 2-го
порядка, перпендикулярными оси n-го порядка.
D2 = {e, 211, 221, 231} (пересечение осей 90 град)
D3 = {e, 211, 221, 231, 31, 32} (60 град)
D4 = {e, 211, 221, 231, 41 , 42 =21, 43 =4-1} (45 град)
D6 = {e, 211, 221, 231, 241, 251, 261, 61 , 62 =31, 63 =21, 64 =32, 65 =6-1} (30 град)

44. Группы с двумя генераторами: два поворота вокруг оси 2 порядка

45. Группы с двумя генераторами: два поворота вокруг оси 2 порядка

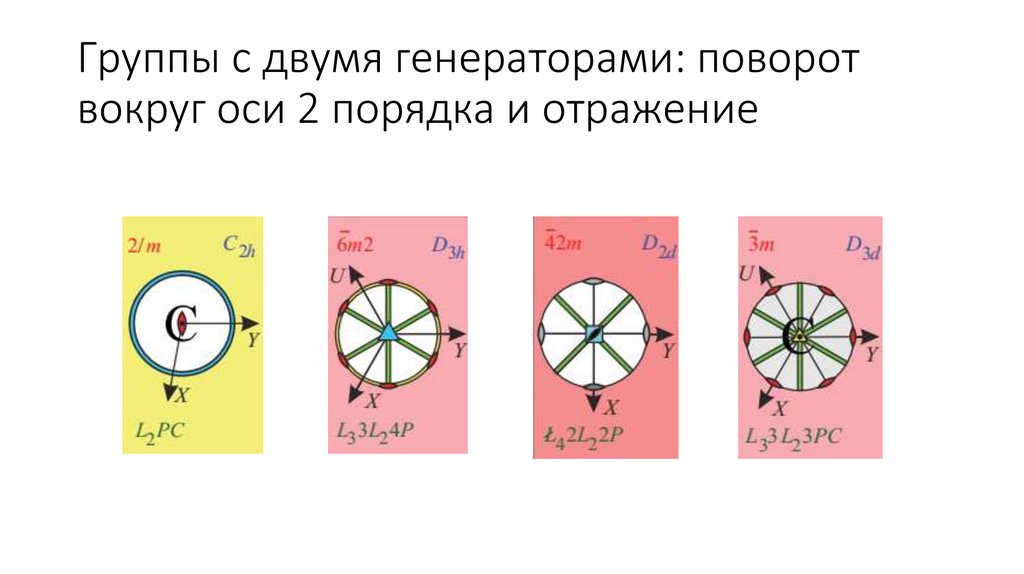
Группы с двумя генераторами: поворот
вокруг оси 2 порядка и отражение
Возникает зеркально-поворотная ось с элементарным углом
поворота 2φ. Допустимый порядок возникающих
кристаллографических осей симметрии определяет возможные
углы φ — как и в предыдущих случаях, их значения могут равняться
лишь 90°, 60°, 45° и 30°.
C2h = {e, m1, 21, ഥ1} (90° между L и m)
D3h = {e, m1, m2, m3, m4, 211, 221, 231, 31, 32, 3ሶ 1, 3ሶ 2} (60° между L и m)
D2d = {e, m1, m2, 211, 221, 4ሶ 1, 4ሶ 2 = 21, 4ሶ 3= 4ሶ -1} (45° между L и m)
D3d = {e, m1, m2, m3, 211, 221, 231, 61, 6ሶ 1, 6ሶ 2=31, 6ሶ 3 = ഥ1, 6ሶ 4 = 32, 6ሶ 5 = 6ሶ -1}
(30° между L и m)

46. Группы с двумя генераторами: поворот вокруг оси 2 порядка и отражение

47. Группы с двумя генераторами: поворот вокруг оси 2 порядка и отражение

Группы с двумя генераторами: поворот вокруг
оси n-го порядка и отражение в
перпендикулярной плоскости
C2h = {e, m1, 21, ഥ1} (как и с осью второго)
C3h = S3 = {e, 3ሶ 1, 3ሶ 2=3-1, 3ሶ 3 = m, 3ሶ 4 = 31, 3ሶ 5 = 3ሶ -1} (ось 3 порядка)
C4h = {e, 41 , 42 =21, 43 =4-1, m, 4ሶ 1, ഥ1, 4ሶ 3= 4ሶ -1} (ось 4 порядка)
C6h = {e, 61 , 62 =31, 63 =21, 64 =32, 65 =6-1, 6ሶ 1, 6ሶ 2=31, 6ሶ 3 = ഥ1, 3ሶ 3 =m, 6ሶ 5 =
3ሶ 5 } (ось 6 порядка)

48. Группы с двумя генераторами: поворот вокруг оси n-го порядка и отражение в перпендикулярной плоскости

49. Группы с двумя генераторами: поворот вокруг оси n-го порядка и отражение в перпендикулярной плоскости

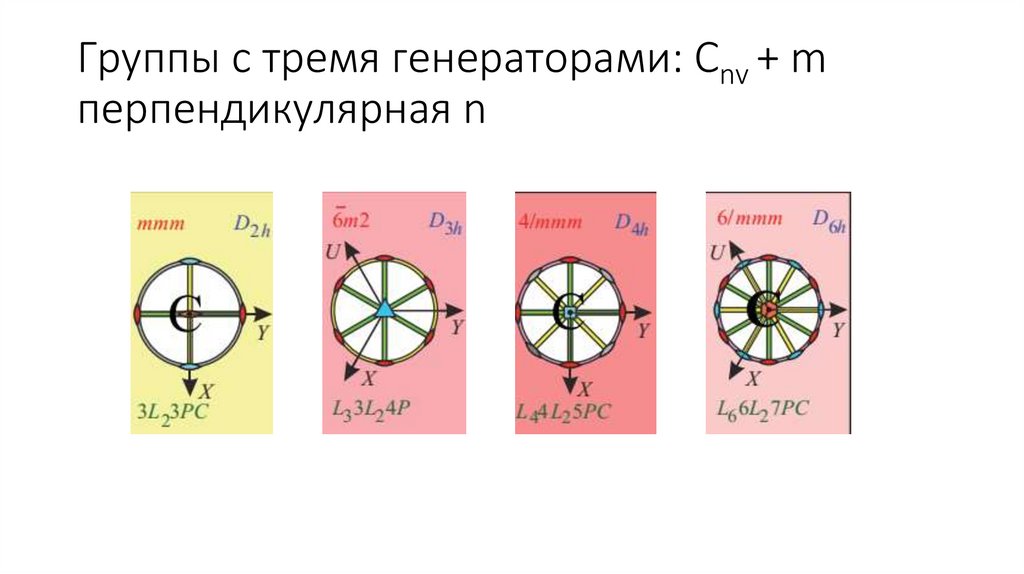
Группы с тремя генераторами: Cnv + m
перпендикулярная n
Возникают взаимно перпендикулярные оси второго порядка.
C2v + m = D2h = {e, 211, 221, 231, m1, m2, m3, ഥ1}
C3v + m = D3h ={e, m1, m2, m3, m4, 211, 221, 231, 31, 32, 3ሶ 1, 3ሶ 2} (то же, что
90° между L и m)
C4v + m = D4h ={e, 41 , 42 =21, 43 =4-1, 211, 221, 231, 241, m1, m2, m3, m4,
m5, ഥ1, 4ሶ 1, 4ሶ 3= 4ሶ -1}
C6v + m = D6h ={e, 61 , 62 =31, 63 =21, 64 =32, 65 =6-1, m1, m2, m3, m4, m5,
m6, m7, 211, 221, 231, 241, 251, 261, ഥ1, 6ሶ 5, 3ሶ 5}

50. Группы с тремя генераторами: Cnv + m перпендикулярная n

51. Группы с тремя генераторами: Cnv + m перпендикулярная n

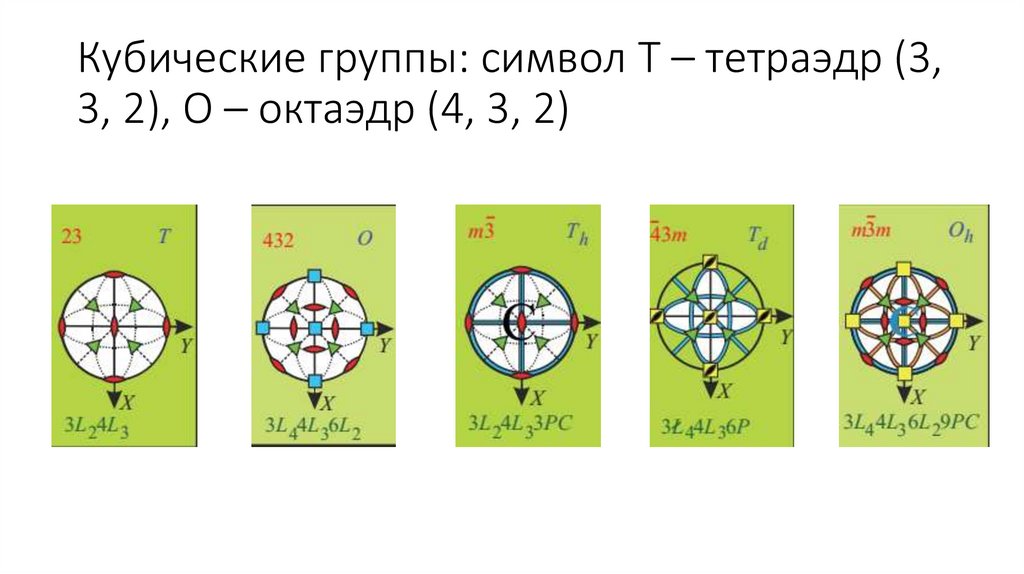
Кубические группы: символ T – тетраэдр (3,
3, 2), О – октаэдр (4, 3, 2)
T = {e, 211, 221, 231, 311, 312, 321, 322, 331, 332, 341, 342} – 12 элементов
O = {e, 211, 221, 231, 241, 251, 261, 311, 312, 321, 322, 331, 332, 341, 342, 411,
412, 413, 421, 422, 423, 431, 432, 433} – 24 элемента
T + m (h – параллельно, v – перпендикулярно, d - диагонально):
Th (Tv) = {e, 211, 221, 231, 311, 312, 321, 322, 331, 332, 341, 342 , m1, m2, m3,
6ሶ 11, 6ሶ 21 , 6ሶ 31 , 6ሶ 41, 6ሶ 15, 6ሶ 25 , 6ሶ 35 , 6ሶ 45} - 24 элемента
Td = {e, 311, 312, 321, 322, 331, 332, 341, 342 , m1, m2, m3, m4, m5, m6, 41ሶ 1, 42ሶ 1,
43ሶ 1, 41ሶ 2 = 211, 42ሶ 2 = 221, 43ሶ 2 = 231, 41ሶ 3, 42ሶ 3, 43ሶ 3} - 24 элемента
Oh = {e, 211, 221, 231, 241, 251, 261, 311, 312, 321, 322, 331, 332, 341, 342 , m1,
m2, m3, m4, m5, m6, m7, m8, m9, 41ሶ 1, 42ሶ 1, 43ሶ 1, 41ሶ 3, 42ሶ 3, 43ሶ 3, ഥ1, 6ሶ 11, 6ሶ 21 , 6ሶ 31 ,
6ሶ 41, 6ሶ 15, 6ሶ 25 , 6ሶ 35 , 6ሶ 45} - 48 элементов

52. Кубические группы: символ T – тетраэдр (3, 3, 2), О – октаэдр (4, 3, 2)

53. Кубические группы: символ T – тетраэдр (3, 3, 2), О – октаэдр (4, 3, 2)

Изоморфные группы: таблицы умножения
C2v
C2h
D2
e
2
m
ഥ1
e
e
2
m
ഥ1
22
2
2
e
ഥ1 m
e
21
m
m
ഥ1 e
21
e
ഥ1
ഥ1 m
e
21
22
23
e
e
21
22
23
21
21
e
23
22
22
23
23
23
22
21
e
2
m1 m2
e
e
2
m1
2
2
e
m2 m1
m2
21
m1 m1
m2 e
2
e
m2 m2 m1 2
e

54. Изоморфные группы: таблицы умножения

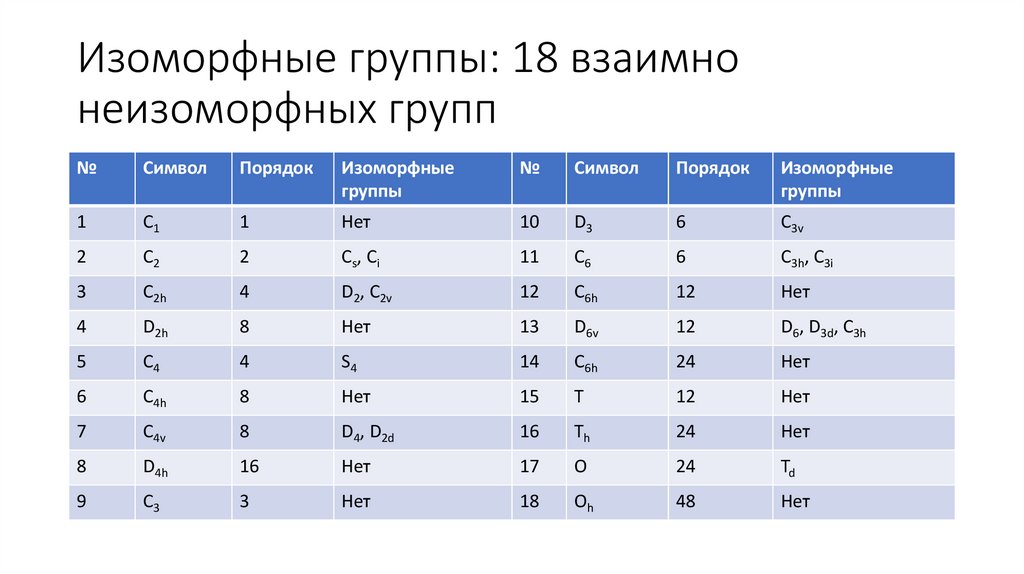
Изоморфные группы: 18 взаимно
неизоморфных групп
№
Символ
Порядок
Изоморфные
группы
№
Символ
Порядок
Изоморфные
группы
1
С1
1
Нет
10
D3
6
С3v
2
С2
2
Сs, Сi
11
С6
6
С3h, С3i
3
С2h
4
D2, С2v
12
С6h
12
Нет
4
D2h
8
Нет
13
D6v
12
D6, D3d, С3h
5
С4
4
S4
14
С6h
24
Нет
6
С4h
8
Нет
15
T
12
Нет
7
С4v
8
D4, D2d
16
Th
24
Нет
8
D4h
16
Нет
17
O
24
Td
9
С3
3
Нет
18
Oh
48
Нет

55. Изоморфные группы: 18 взаимно неизоморфных групп

Задачи
1. Вывести группу симметрии, приняв за генераторы операции
отражения в двух взаимно перпендикулярных плоскостях и
поворот вокруг оси второго порядка, перпендикулярной к
одной из плоскостей. Определить порядок группы, изобразить
элементы симметрии на стереографической проекции и дать
обозначение по Шенфлису и Герману-Могену.
2. Записать таблицу умножения для ТГС 32. Построить
стереографическую проекцию ее элементов симметрии.