7e3c00cad4f646f888cc18c65cd2b37c (1)

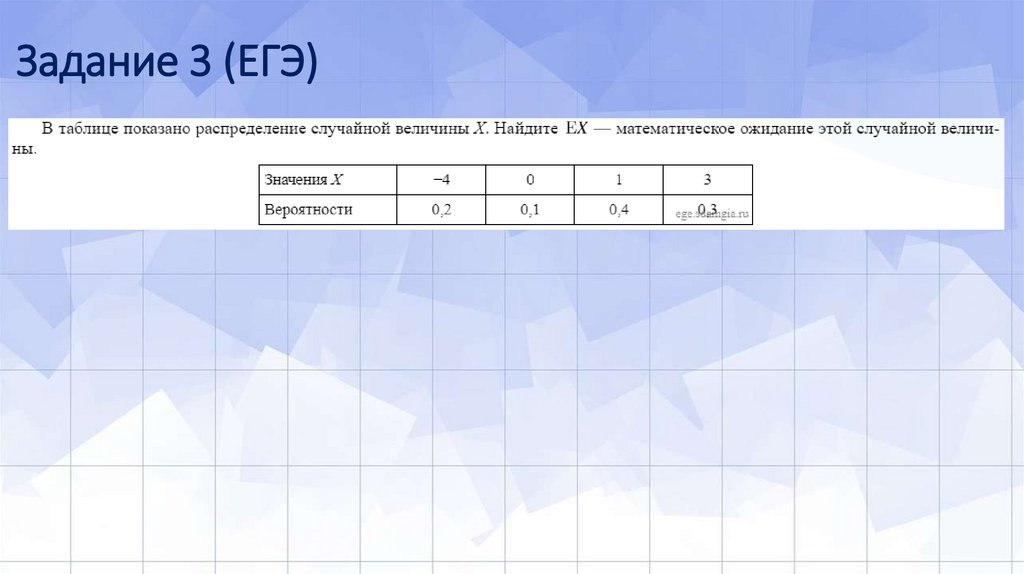
1. Математическое ожидание суммы случайных величин

2.

Термин “математическое ожидание”
введён Пьером Симоном маркизом
де Лапласом (1795) и произошёл от
понятия
“ожидаемого
значения
выигрыша”, впервые появившегося в
17 веке в теории азартных игр в
трудах Блеза Паскаля и Христиана
Гюйгенса. Однако первое полное
теоретическое осмысление и оценка
этого понятия даны Пафнутием
Львовичем Чебышёвым (середина 19
века).
Пьер Симон маркиз де Лапласа
П.Л.Чебышев

3.

Математическим ожиданием дискретной случайной величины
называется сумма произведений ее возможных значений на
соответствующие им вероятности. Иногда математическое ожидание
называют взвешенным средним, так как оно приближенно равно
среднему арифметическому наблюдаемых значений случайной величины
при большом числе опытов. Математическое ожидание вычисляется по
формуле:
М X p1 x1 p2 x2 p3 x3 ... pn xn

4.

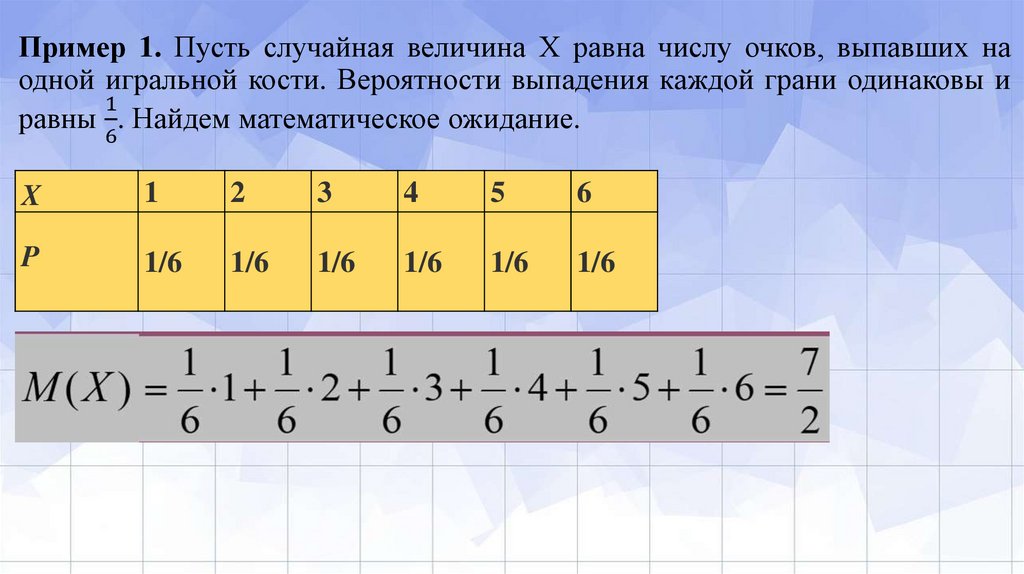
Пример 1. Пусть случайная величина Х равна числу очков, выпавших на
одной игральной кости. Вероятности выпадения каждой грани одинаковы и
1
равны . Найдем математическое ожидание.
6
X
1
2
3
4
5
6
P
1/6
1/6
1/6
1/6
1/6
1/6

5. Физический смысл математического ожидания

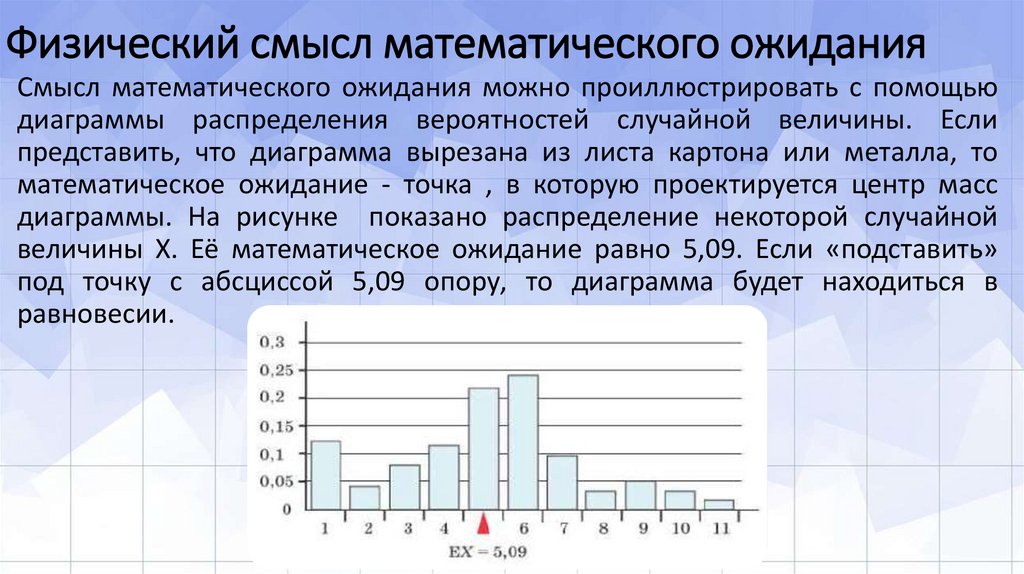
Смысл математического ожидания можно проиллюстрировать с помощью
диаграммы распределения вероятностей случайной величины. Если
представить, что диаграмма вырезана из листа картона или металла, то
математическое ожидание - точка , в которую проектируется центр масс
диаграммы. На рисунке показано распределение некоторой случайной
величины Х. Её математическое ожидание равно 5,09. Если «подставить»
под точку с абсциссой 5,09 опору, то диаграмма будет находиться в
равновесии.

6. Задание 1

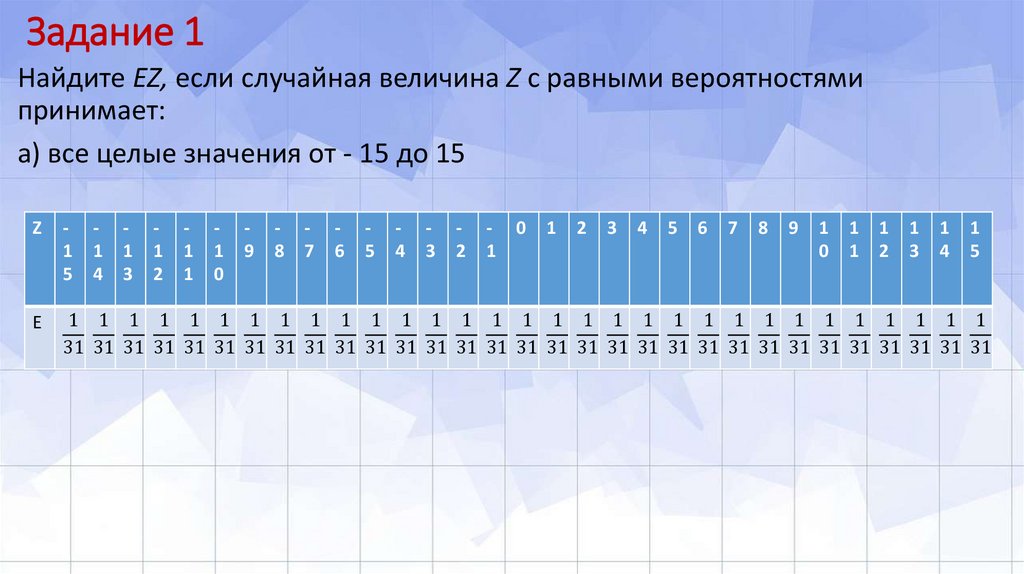
Найдите EZ, если случайная величина Z с равными вероятностями
принимает:
а) все целые значения от - 15 до 15
Z
1
5
1
4
1
3
1
2
1
1
1
0
9
8
7
6
5
4
3
2
1
0
1
2
3
4
5
6
7
8
9
1
0
1
1
1
2
1
3
1
4
1
5
E
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
31 31 31 31 31 31 31 31 31 31 31 31 31 31 31 31 31 31 31 31 31 31 31 31 31 31 31 31 31 31 31

7. Задание 2

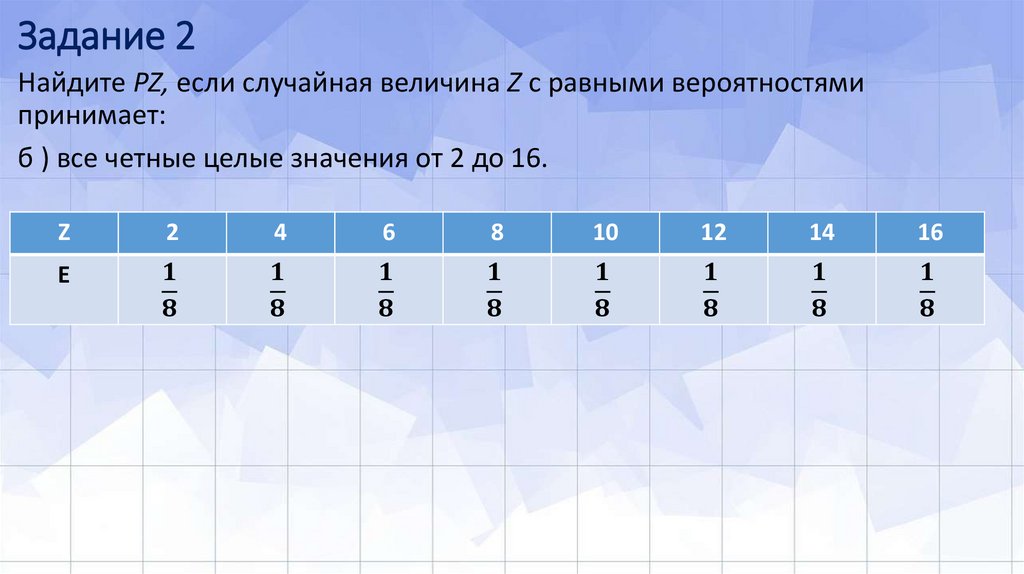
Найдите PZ, если случайная величина Z с равными вероятностями
принимает:
б ) все четные целые значения от 2 до 16.
Z
2
4
6
8
10
12
14
16
E