Системы счисления (1)

1.

Системы счисления

2.

Система счисления – это способ записи чисел
с помощью заданного набора специальных
знаков (цифр)
Системы счисления
непозиционные
вес цифры не зависит от
её позиции в числе
Единичная
Римская
(цифры I, V, X, L, C, D, M)
Древнеегипетская
Древнегреческая
Славянская
кириллическая
позиционные
вес каждой цифры изменяется
в зависимости от её положения
Двадцатеричная народов
племени Майя
Вавилонская
Древнекитайская
десятеричная
Двоичная
Десятичная
(0 1 2 3 4 5 6 7 8 9)

3.

НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Алфавит системы содержит неограниченное
количество символов.
Единичная ("палочная”, “унарная”) система
счисления

4.

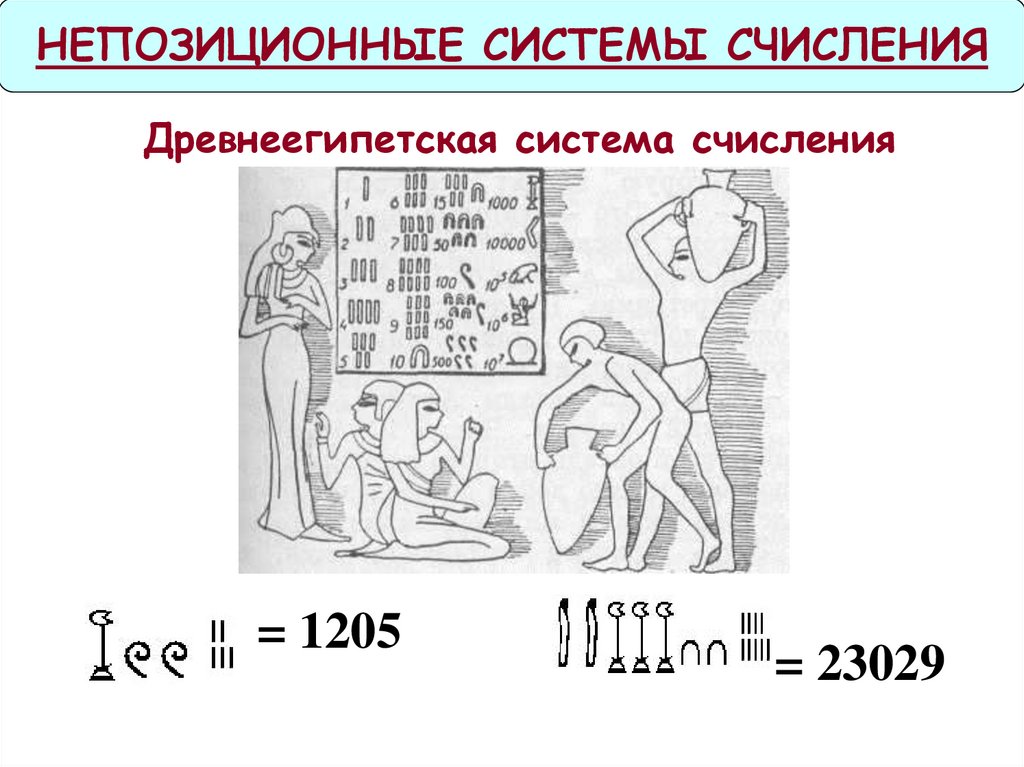
НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Древнеегипетская система счисления
= 1205
= 23029

5.

НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Древнегреческие системы счисления
Древнегреческая аттическая пятеричная
= 256
= 2051
= 382
Древнегреческая ионийская десятеричная алфавитная
= 265
= 503
= 731

6.

НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Славянская система счисления
=
=

7.

НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Римская система счисления - для записи
чисел используются буквы латинского алфавита
Для записи чисел используются два правила:
1- каждый меньший знак, поставленный слева от
большего, вычитается из него;
2- каждый меньший знак, поставленный справа от
большего, прибавляется к нему.
IX
9 = 10 -1
XII
12 = 10 + 1 + 1

8.

Недостатки непозиционных системы
счисления
1. Существует постоянная потребность введения
новых знаков для записи больших чисел.
2. Невозможно представлять дробные и
отрицательные числа.
3. Сложно выполнять арифметические операции, так
как не существует алгоритмов их выполнения. В
частности, у всех народов наряду с системами
счисления были способы пальцевого счета, а у
греков был счетная доска абак – что-то наподобие
наших счетов.
Но мы до сих пор пользуемся элементами
непозиционной системы счисления в обыденной
речи, в частности, мы говорим сто, а не десять
десятков, тысяча, миллион, миллиард, триллион.

9.

.
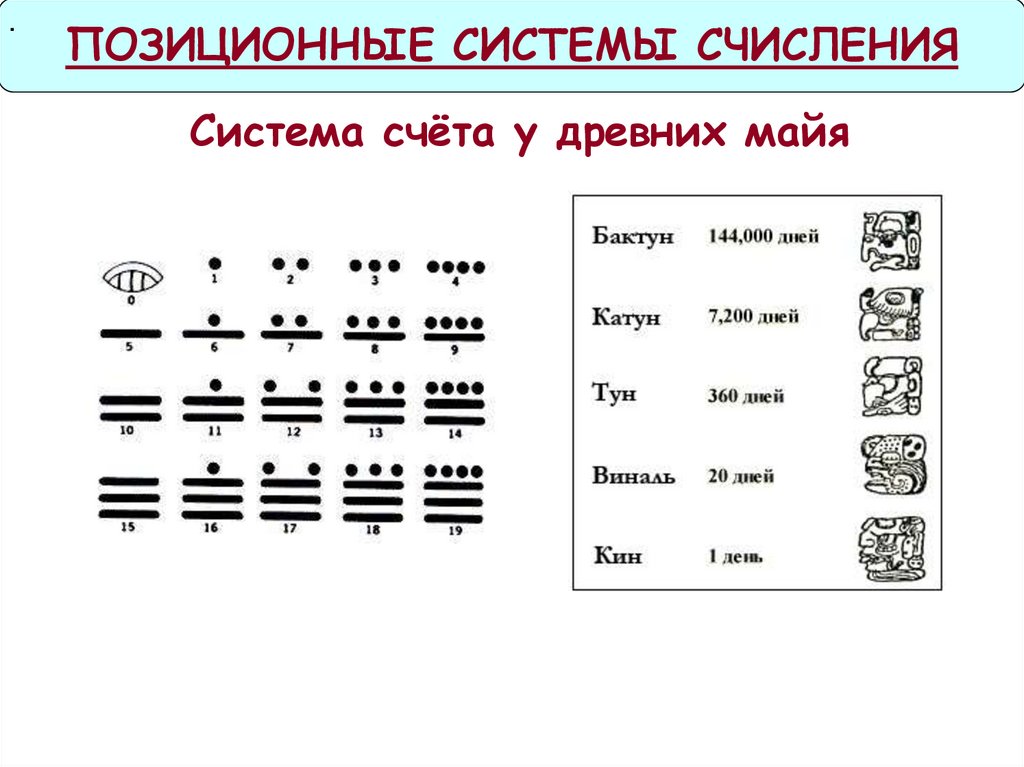
ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Система счёта у древних майя

10.

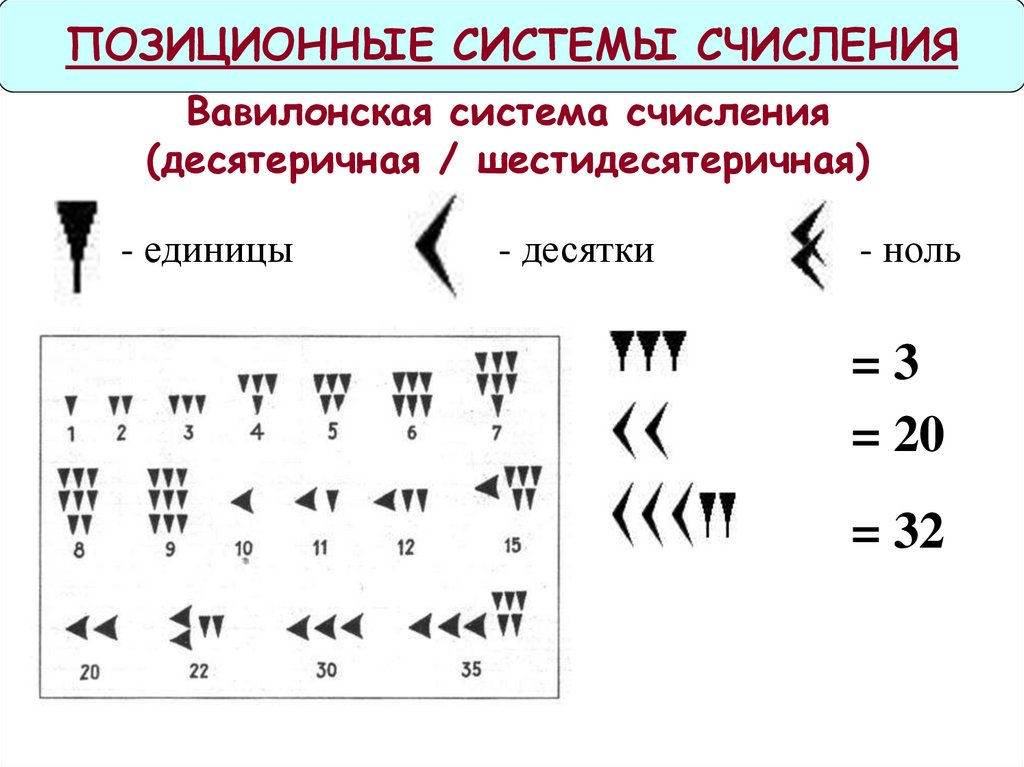
ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Вавилонская система счисления
(десятеричная / шестидесятеричная)
- единицы
- десятки
- ноль
=3
= 20
= 32

11.

ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Основание системы – это количество
различных знаков, используемых для
изображения чисел в данной системе.
Троичная
0, 1, 2
Пятеричная 0, 1, 2, 3, 4
Двенадцатеричная
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B
Позиция цифры в числе называется
разрядом.

12.

ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Десятичная система счисления

13.

Задачи
1. Записать число 444; 1986 в римской системе
счисления.
2. Какие числа записаны с помощью римских цифр:
MMIV, LXV, CMLXIIV?
3. Запишите число 555:
А) в древнеегипетской системе счисления;
Б) в римской системе счисления;
В) в древнеславянской системе счисления.
4. Некоторые римские цифры легко изобразить с
помощью палочек. Исправьте неверные равенства,
переложив с одного места на другое только одну
палочку.
VII – V = XI
VI – I = III
IX – V = VI
VIII – III = X

14.

В вычислительной технике
применяют 4 системы счисления:
• Двоичная – 0, 1 (основание с.с. 2)
• Десятичная – 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
(основание с.с. 10)
• Восьмеричная – 0, 1, 2, 3, 4, 5, 6, 7
(основание с.с. 8)
• Шестнадцатеричная – 0, 1, 2, 3, 4, 5, 6,
7, 8, 9, A, B, C, D, E, F (основание с.с. 16)

15.

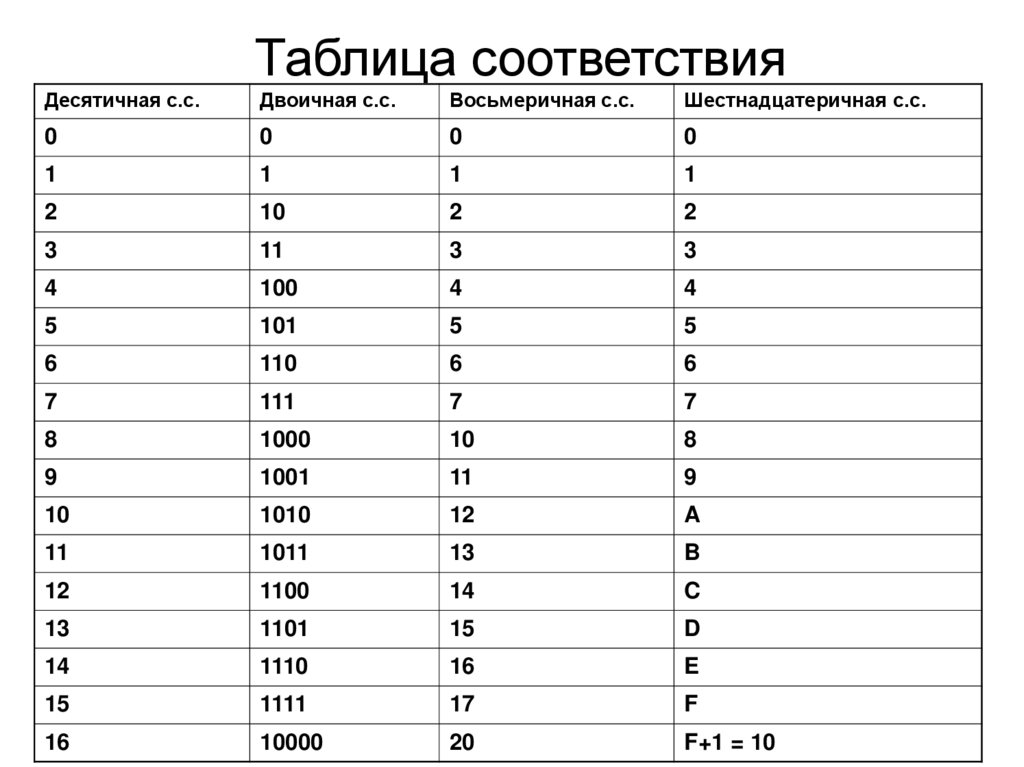
Таблица соответствия
Десятичная с.с.
Двоичная с.с.
Восьмеричная с.с.
Шестнадцатеричная с.с.
0
0
0
0
1
1
1
1
2
10
2
2
3
11
3
3
4
100
4
4
5
101
5
5
6
110
6
6
7
111
7
7
8
1000
10
8
9
1001
11
9
10
1010
12
A
11
1011
13
B
12
1100
14
C
13
1101
15
D
14
1110
16
E
15
1111
17
F
16
10000
20
F+1 = 10

16.

Развернутая форма представления
целого десятичного числа
3 2 1 0
238110 = 2000 + 300 + 80 + 1 =
2·103 + 3·102 + 8·101 + 1·100
Развернутая форма представления
десятичного дробного числа
1 0
-1 -2
23,8110 = 20 + 3 + 0,8 + 0,01 =
2·101 + 3·100 + 8·10-1 + 1·10-2

17.

Задачи
№1. Сравните числа:
А) 510 и 58
Б) 11112 и 11118
№2. Запишите в развернутом виде следующие числа:
А) А10 = 3457,78;
Б)А5 = 231,44;
В) А16 = Е2ЗС,1А;
Г)А2= 11001,101.
№3. Запишите в свернутой форме следующие числа:
А) А16 = А*161+ 1*160+7*16-1+5*16-2;
Б) А10 = 9*101+1*100+ 5*10-1+3*10-2.

18.

Перевод чисел
1.
Перевод
чисел
из
любой
позиционной системы в десятичную
2 1 0
3125 = 3·52 + 1·51 + 2·50 =75+5+2
=8210

19.

Задачи
№1. Запишите в десятичной системе счисления
следующие числа:
А9 = 7688; А5 = 432,1; А3 =120; А4 = 102,31.
№2. Представьте в десятичной системе
счисления число 101,1, считая
записанным в системах счисления от 2-ой
до 9-ой.
№3. В коробке лежит 318 шар. Среди них 128
красных и 178 желтых. Докажите, что
здесь нет ошибки.
№4. В классе 11112 девочек и 10102
мальчиков. Сколько учеников в классе?

20.

2.
Перевод целых чисел из десятичной
системы счисления в любую другую

21.

Задание: переведите числа из
десятичной системы счисления в
другую позиционную систему.
2310= ?2
101112
13910= ? 8
2138
16310 = ? 16
A316

22.

Перевод правильных дробей из десятичной
системы счисления в любую другую
3.
Пример. Переведем число 0,3610 в А2, А8, А16:

23.

Задачи
№1. Переведите числа из десятичной системы
счисления:
А) 0, 141 в пятеричную систему счисления с точностью
до пяти знаков.
Б) 0, 675 в троичную систему счисления с точностью до
пяти знаков.
В) 0, 2004 в восьмеричную систему счисления с
точностью до пяти знаков.
Г) 0,7982 в двоичную систему счисления с точностью до
шести знаков.
№2. Перевести числа в троичную и пятеричную
системы счисления, оставив четыре знака после
запятой:
А) 30,5; 36,12; 126,33.
Б) 74,222; 112,64; 80,88.