Системы счисления

1.

Системы счисления

2.

План
• Истории
• Основные определения
• Позиционные и непозиционные системы счисления
• Перевод чисел из 10-й СС в другую
•…

3.

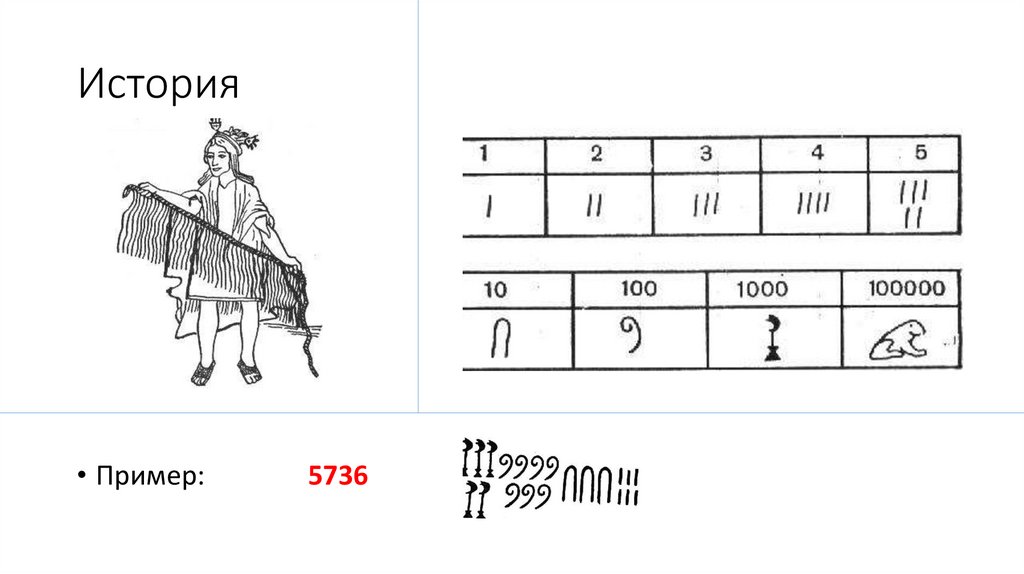
История
• Пример:
5736

4.

Пример записи чисел на Руси
• Звезда – тысяча рублей
• Колесо – сто рублей
• Квадрат – десять рублей
• Х – рубль
• | – копейку.
• «Дабы не можно было сделать здесь никаких прибавлений, все
таковые знаки очерчивать кругом прямыми линиями».

5.

Определение
• Системы счисления (СС) – совокупность приемов и правил
наименования и обозначения чисел, позволяющих установить
взаимно однозначное соответствие между любым числом и его
представлением в виде конечного числа символов.
• Алфавит – { слова или знаки }
• Пример: 10-я СС – { 0,1,2,3,4,5,6,7,8,9 } – алфавит

6.

Непозиционные системы счисления
• Непозиционная система счисления — система, в которой
символы, обозначающие то или иное количество, не меняют
своего значения в зависимости от местоположения (позиции) в
изображении числа.
• Пример: 12 = ||| ||| ||| ||| – алфавит { | }

7.

Непозиционные СС: римская СС
• Пример: римская СС
Римские цифры
I
V
X
L
C
D
M
Значение (обозначаемое число)
1
5
10
50
100
500
1000
• Правила записи чисел:
• 1) если цифра слева меньше, чем цифра справа, то левая цифра вычитается из правой
(IV: 1 < 5, следовательно, 5 – 1 = 4, XL: 10 < 50, следовательно, 50 - 10 = 40)
• 2) если цифра справа меньше или равна цифре слева, то эти цифры складываются (VI:
5+1 = 6, VIII: 5 + 1 + 1 + 1 = 8, XX: 10 + 10 = 20)
• Пример: число 1964 – MCMLXIV - (М - 1000, СМ - 900, LX - 60, IV - 4)

8.

Задание
Запишите числа в римской системе:
• 2007
• 448
• 1954
Запишите числа в десятичной системе:
• MCDXXIII
• LXXIX
• MMCXLI

9.

Позиционные системы счисления
• Систему счисления, в которой значение цифры определяется ее местоположением
(позицией) в изображении числа, называют позиционной.
• Упорядоченный набор символов (цифр) {a0,a1,...,an}, используемый для
представления любых чисел в заданной позиционной системе счисления, называют
ее алфавитом.
• Количество различных цифр, используемых для изображения чисел в данной
системе счисления – основание СС
• Пример:
10-я СС – { 0,1,2,3,4,5,6,7,8,9 } – алфавит
• Пример:
222.22 = 2 * 102 + 2 * 101 + 2 * 100 + 2 * 10-1+ 2 * 10-2
Развернутая
запись числа

10.

Примеры развернутой записи чисел
725 = 7 * 102 + 2 * 101 + 5 * 100
1304.5 = 1 * 103 + 3 * 102 + 0 * 101 + 4 * 100 + 5 * 10-1
50328.15 = 5 * 104 +0 * 103 + 3 * 102 + 2 * 101 + 8 * 100 + 1 * 10-1 + 5 * 10-2
Полином: A10 = an * 10n + an-1 * 10n-1 + … + a1 * 101 + a0 * 100 + a-1 * 10-1 + … + a-m * 10-m
A10 = an an-1 … a1 a0 . a-1 …a-m

11.

Задание
Запишите в развернутом виде числа:
• А8=143511,62
• А2=100111
• А10=143,511
• А16=1А3,5С1
Запишите в свернутой форме число:
• 9*101+1*100+5*10-1+3*10-2 =
• A*162+1*161+C*160+3*16-1 =

12.

Примеры различных систем счисления

13.

Пример: 3510

14.

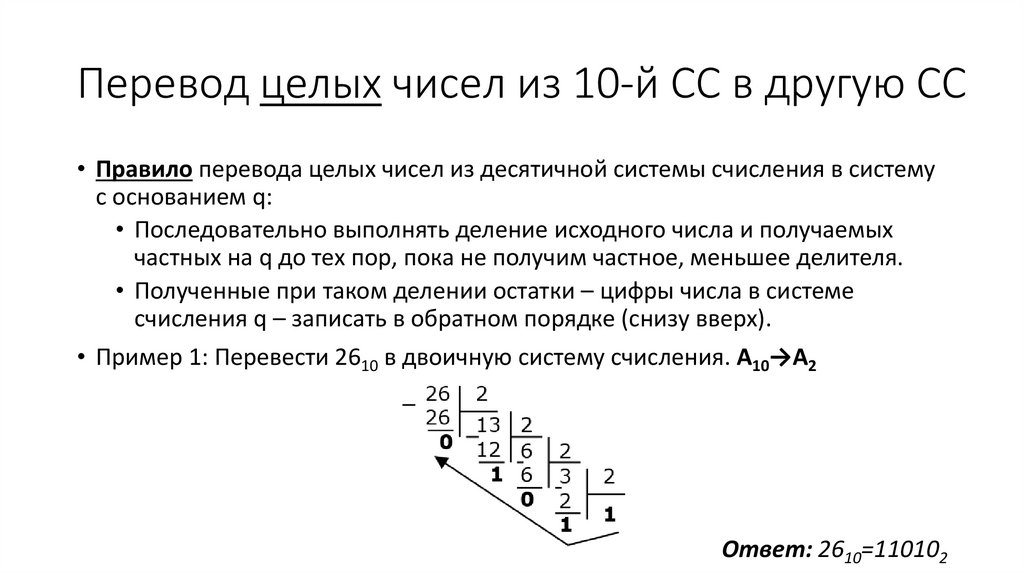
Перевод целых чисел из 10-й СС в другую СС
• Правило перевода целых чисел из десятичной системы счисления в систему
с основанием q:
• Последовательно выполнять деление исходного числа и получаемых
частных на q до тех пор, пока не получим частное, меньшее делителя.
• Полученные при таком делении остатки – цифры числа в системе
счисления q – записать в обратном порядке (снизу вверх).
• Пример 1: Перевести 2610 в двоичную систему счисления. А10→А2
Ответ: 2610=110102

15.

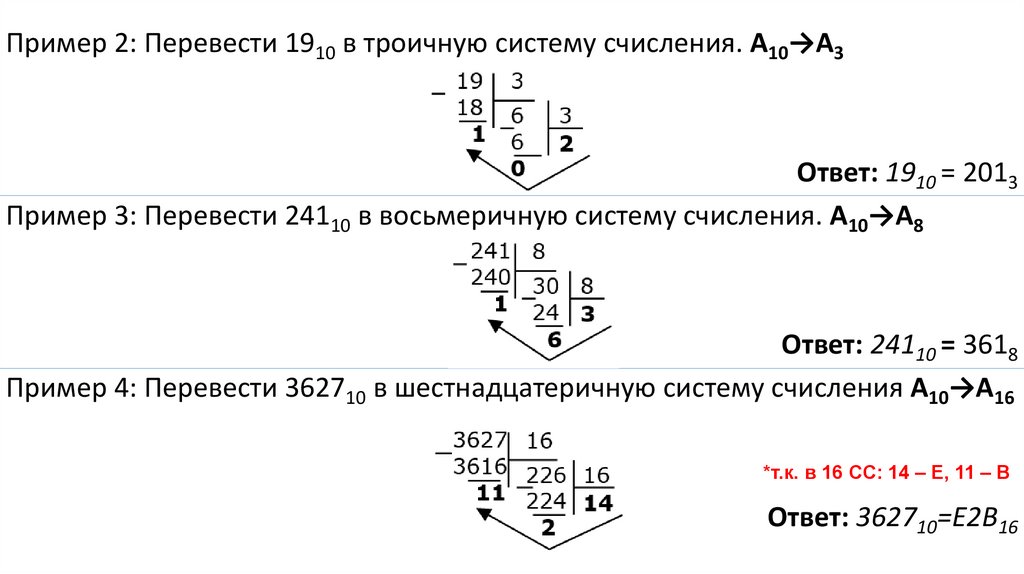
Пример 2: Перевести 1910 в троичную систему счисления. А10→А3
Ответ: 1910 = 2013
Пример 3: Перевести 24110 в восьмеричную систему счисления. А10→А8
Ответ: 24110 = 3618
Пример 4: Перевести 362710 в шестнадцатеричную систему счисления А10→А16
*т.к. в 16 СС: 14 – Е, 11 – В
Ответ: 362710=E2B16

16.

Задание
• Переведите числа из десятичной системы счисления в другую.
• а) 24510 →
А2
• б) 40410 →
А8
• в) 198710 →
А2
• г) 67310 →
А16
• д) 16110 →
А3
• е) 4534810 →
А16
• ж) 33310 →
А5
• з) 44410 →
А7

17.

Перевод дробных чисел
из 10-й СС в другую СС
• Правило перевода дробных чисел из десятичной системы счисления в
систему с основанием q:
• Последовательно выполнять умножение исходного числа и получаемых дробные части
на q до тех пор, пока дробная часть не станет равна нулю или не достигнем требуемую
точность.
• Полученные при таком умножении целые части - числа в системе счисления q –
записать в прямом порядке (сверху вниз).
Пример 1: Перевести 0,562510 → А2
Ответ: 0,562510=0,10012

18.

• Пример 2: Перевести 0,562510 восьмеричную систему счисления. А10→А8
Ответ: 0,562510=0,528
• Перевести 0,66510 в двоичную систему счисления. А10→А2
Ответ: 0,66510=0,101012

19.

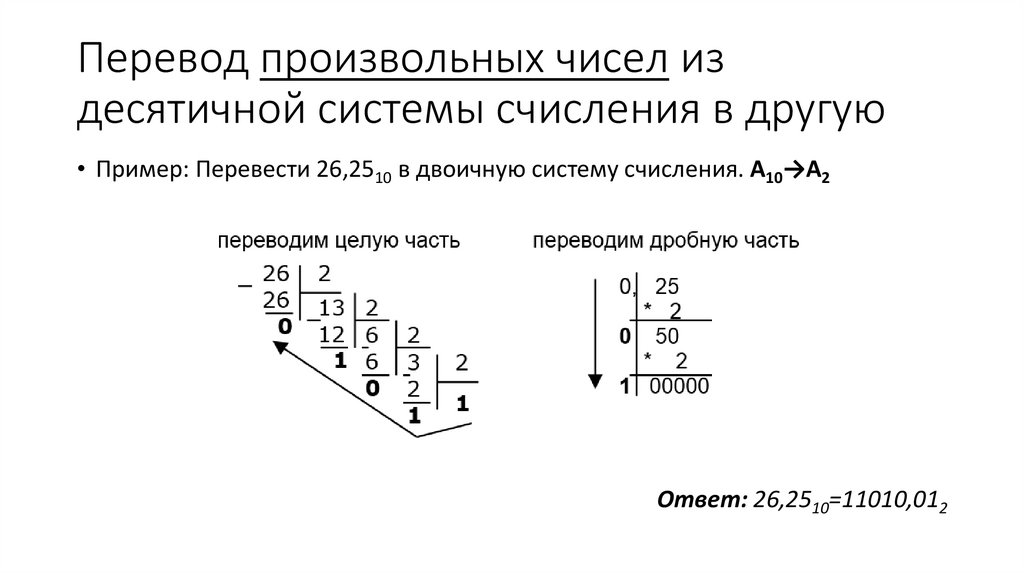
Перевод произвольных чисел из
десятичной системы счисления в другую
• Пример: Перевести 26,2510 в двоичную систему счисления. А10→А2
Ответ: 26,2510=11010,012

20.

Перевод чисел из любой СС в 10-ю СС
• Правило: Для того чтобы число из любой системы счисления перевести в
десятичную систему счисления, необходимо его представить в развернутом
виде и произвести вычисления.
• Пример 1: Перевести число 1101102 → ( ____ )10
5 4 3 2 1 0
1 1 0 1 1 0 2 = 1*25 + 1*24 + 0*23 + 1*22 + 1*21 + 0*20 = 32 + 16 + 4 + 2 = 5410

21.

• Пример 2: Перевести число 110,102 → ( ____ )10
2 1 0 -1 -2
1 0 1,0 1 2 = 1*22 + 0*21 + 1*20 + 0*2-1 + 1*2-2 = 4+0+1+0+0,25 =5,2510
• Пример 3: Перевести число 1637 → ( ____ )10
210
1637 = 1*72 + 6*71 + 3*70 = 49+42+3= 9410
• Пример 4: Перевести число 2Е16 → ( ____ )10
1 0
2 Е16 = 2*161 +14*160 = 32 +14 = 4610.

22.

Перевод чисел ( ____ )2 → ( ____ )8
• Правило: Чтобы перевести целое двоичное число в восьмеричную (8=23)
систему счисления необходимо:
• разбить данное число справа налево на группы по 3 цифры в каждой;
• рассмотреть каждую группу и записать ее соответствующей цифрой восьмеричной
системы счисления.
• Пример 1: Перевести число 111 110 000 010 1102 в 8-ю систему счисления
Ответ: 111 110 000 010 1102= 760268

23.

Перевод чисел ( ____ )2 → ( ____ )16
• Правило: Чтобы перевести целое двоичное число в шестнадцатеричную
(16 = 24) систему счисления необходимо:
• разбить данное число справа налево на группы по 4 цифры в каждой;
• рассмотреть каждую группу и записать ее соответствующей цифрой восьмеричной
системы счисления.
• Пример 1: Перевести число 111100000101102 в 16-ю систему счисления
Ответ: 111100000101102= 3С1616

24.

Пример с дробной частью
• Пример: 111100001,01112 → ( ____ )8
• Пример: 11101001000,110100102 → ( ____ )16

25.

Примеры для СРС
• Перевести числа в восьмеричную и шестнадцатеричную системы
счисления:
• а) 11010001010112
• б) 100000011,0001011102
• в) 10010111011101,111010112
• г) 111110000000111111111,0000011111000001111101012

26.

Арифметические действия

27.

Сложение в двоичной системе
Пример: Сложить числа 1112 и 102
Решение:
111
+
10
1001
Проверка: 1112 = 710, 102 = 210, 10012 =910
7+2=9

28.

Пример сложения
Пример: Сложить числа 111112 и 1112
Решение:
11111
+
111
100110
Проверка:
111112=1*24+1*23+1*22+1*21+1*20=16+8+4+2+1=3110
1112 = 710
1001102=1*25+0+0+1*22+1*21+0=32+4+2=3810
31+7=38

29.

Пример сложения
Пример: Сложить числа 11111,1012+101,112.
Решение:
11111,101
+
101,11
100101,011

30.

Вычитание в двоичной системе
Пример: Из числа 10012 вычесть число 1112
Решение:
1001
111
10
Проверка: 10012 =9, 1112 = 7, 102 = 2, 9-7=2

31.

Примеры вычитания
Пример: из 1000012 вычесть число 1112
Решение:
100001
-
111
11010
Пример: из 100101,012 вычесть число 111,1112
Решение:
100101,010
111,111
11101,101

32.

Умножение в двоичной СС
Пример: Умножить число 1012 на 1102
*
+
+
101
110
000
1010
10100
11110

33.

Умножение в двоичной СС
Пример: Умножить число 1011,012 на 111,112
1011,01
*
111,11
101101
1011010
+ 010110100
101101000
1011010000
10110100000
1010111,0011

34.

Сложение и вычитание в 8-й СС
+
-
634
275
1131
305,40
+
24,75
332,35
634
275
337
305,40
24,75
332,35

35.

Сложение и вычитание в 16-й СС
+
E5F6
A07
EFFD

36.

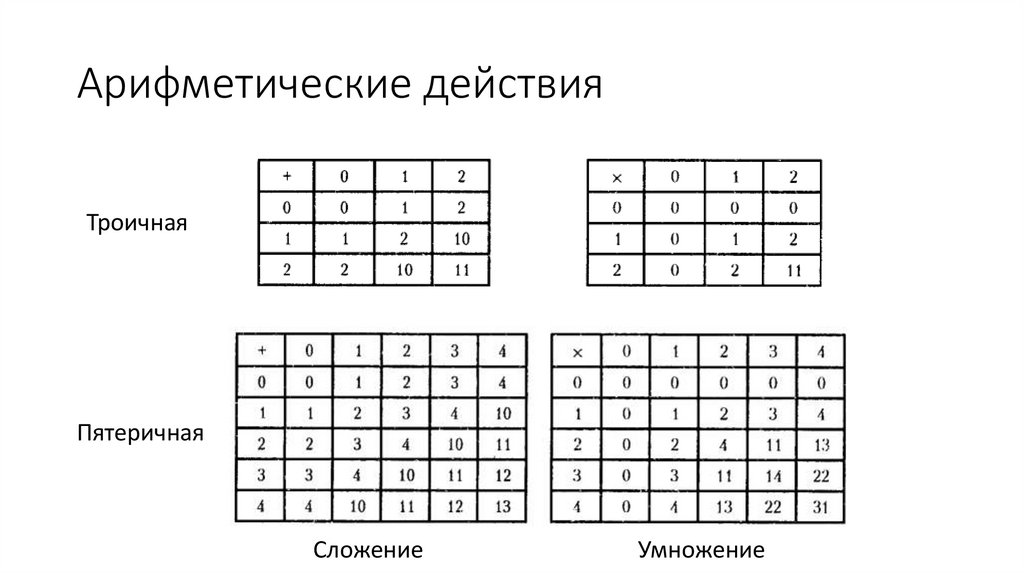
Арифметические действия
Троичная
Пятеричная
Сложение
Умножение

37.

Сложение в 3-й СС и 5-й СС