Гармонические электромагнитные колебания в колебательном контуре

1. Гармонические электромагнитные колебания в колебательном контуре. Формула Томсона.

ГАРМОНИЧЕСКИЕ ЭЛЕКТРОМАГНИТНЫЕ
КОЛЕБАНИЯ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ.
ФОРМУЛА ТОМСОНА.
Федоров А.М. – учитель физики Кюкяйской
СОШ Сунтарского улуса Республики Саха

2. Колебания в контуре

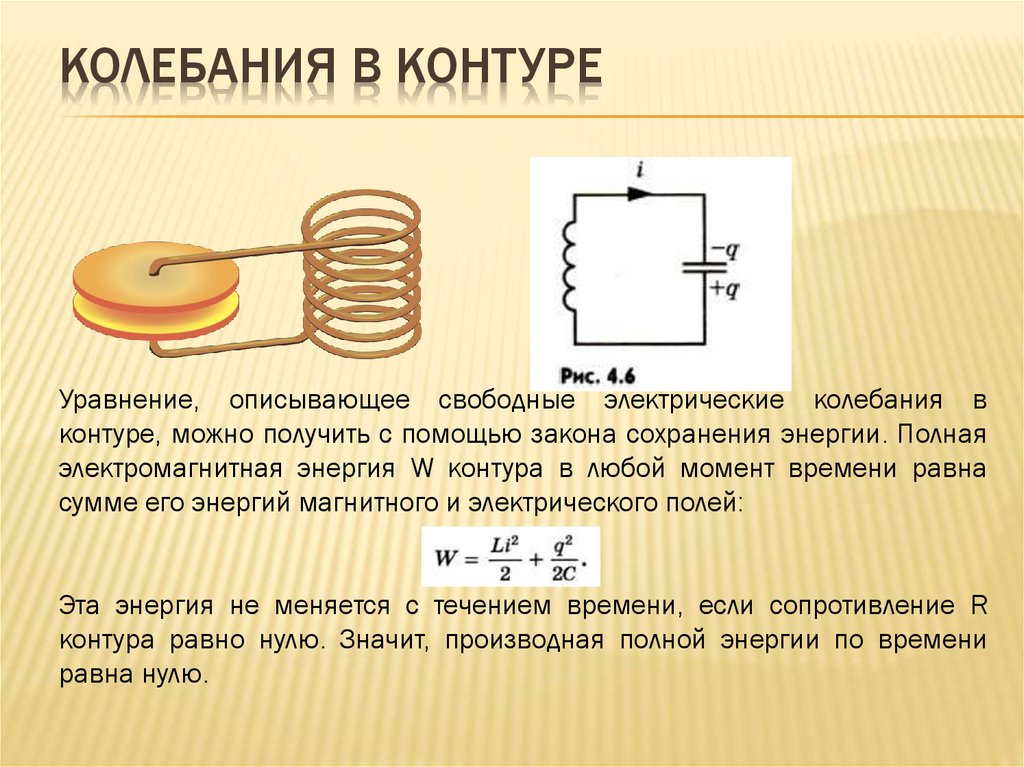
КОЛЕБАНИЯ В КОНТУРЕ
Уравнение, описывающее свободные электрические колебания в
контуре, можно получить с помощью закона сохранения энергии. Полная
электромагнитная энергия W контура в любой момент времени равна
сумме его энергий магнитного и электрического полей:
Эта энергия не меняется с течением времени, если сопротивление R
контура равно нулю. Значит, производная полной энергии по времени
равна нулю.

3. Решение уравнения колебаний

РЕШЕНИЕ УРАВНЕНИЯ КОЛЕБАНИЙ
Следовательно, равна нулю сумма производных по времени от энергий
магнитного и электрического полей:
Физический смысл уравнения (4.5) состоит в том, что скорость изменения
энергии магнитного поля по модулю равна скорости изменения энергии
электрического поля; знак «—» указывает на то, что, когда энергия
электрического поля возрастает, энергия магнитного поля убывает (и
наоборот).
Вычислив производные в уравнении (4.5), получим

4. Решение уравнения колебаний

РЕШЕНИЕ УРАВНЕНИЯ КОЛЕБАНИЙ
Но производная заряда по времени представляет собой силу тока в
данный момент времени:
Поэтому уравнение (4.6) можно переписать в следующем виде:
Производная силы тока по времени есть не что иное, как вторая
производная заряда по времени, подобно тому как производная скорости
по времени (ускорение) есть вторая производная координаты по времени.
Подставив в уравнение (4.8) i' = q" и разделив левую и правую части этого
уравнения на Li, получим основное уравнение, описывающее свободные
электрические колебания в контуре:

5. Формула Томсона

ФОРМУЛА ТОМСОНА
В уравнении (3.11) коэффициент представляет собой квадрат собственной
частоты колебаний. Поэтому и коэффициент в уравнении (4.9) также
представляет собой квадрат циклической частоты — в этот раз для свободных
электрических колебаний:
Период свободных колебаний в контуре, таким образом, равен:
Формула (4.11) называется формулой Томсона в
честь английского физика У. Томсона (Кельвина),
который ее впервые вывел.

6. Гармонические колебания заряда и тока

ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ ЗАРЯДА И
ТОКА
Подобно тому как координата при механических колебаниях (в случае,
когда в начальный момент времени отклонение тела маятника от
положения равновесия максимально) изменяется со временем по
гармоническому закону:
х = хm cos ω0t,
заряд конденсатора меняется с течением времени по такому же закону:
q = qm cos ω0t,
(4.12)
где qm — амплитуда колебаний заряда.
Сила тока также совершает гармонические колебания:
где Im = qmω0 — амплитуда колебаний силы тока.
Точно так же колебания скорости тела в случае пружинного или
математического маятника опережают на π/2 колебания координаты
(смещения) этого тела.

7. Графики колебаний заряда и силы тока

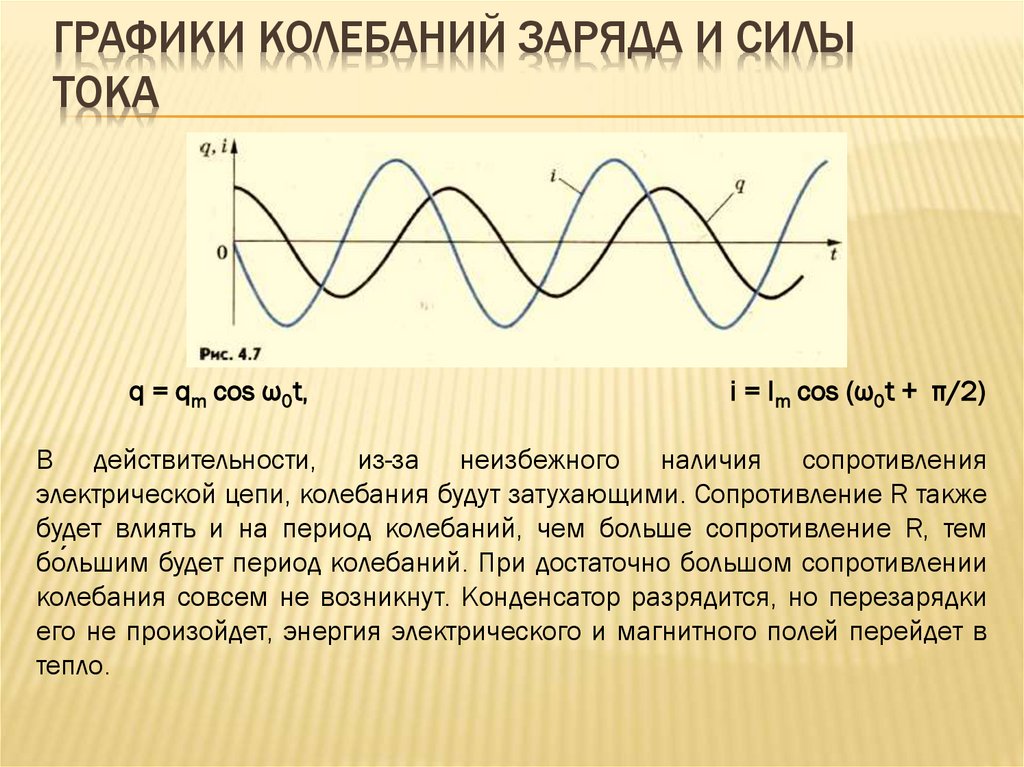
ГРАФИКИ КОЛЕБАНИЙ ЗАРЯДА И СИЛЫ
ТОКА
q = qm cos ω0t,
i = Im cos (ω0t + π/2)
В действительности, из-за неизбежного наличия сопротивления
электрической цепи, колебания будут затухающими. Сопротивление R также
будет влиять и на период колебаний, чем больше сопротивление R, тем
бо́льшим будет период колебаний. При достаточно большом сопротивлении
колебания совсем не возникнут. Конденсатор разрядится, но перезарядки
его не произойдет, энергия электрического и магнитного полей перейдет в
тепло.

8. Упражнения

УПРАЖНЕНИЯ
1. Определи электроёмкость конденсатора, если напряжение между его
обкладками U= 4В, а его заряд q=6⋅10−4 Кл. (Ответ округли до
десятых.)
2. Конденсатору ёмкостью 5 мкФ сообщили заряд 2 мкКл. Какова
энергия заряженного конденсатора? (Ответ округли до сотых.)
3. Определи период собственных колебаний колебательного контура, если
индуктивность катушки L= 18 мкГн, а ёмкость конденсатора C= 750 пФ.
(Ответ округли до сотых.)
4. Какой величины заряд сосредоточен на каждой из обкладок
конденсатора ёмкостью 13 мкФ, заряженного до напряжения 127 В?
5. Ключ K переводят из положения 1 в положение 2. Как при этом
изменяется период собственных электромагнитных колебаний в
данном контуре?
• станет меньше в 4 раза
• станет больше в 4 раза
• станет меньше в 2 раза
• станет больше в 2 раза
• не изменится

9. Домашнее задание

ДОМАШНЕЕ ЗАДАНИЕ
1. Какую ёмкость должен иметь конденсатор, чтобы при подключении к
источнику напряжения 5,5 В его энергия равнялась энергии
падающей со скоростью 10 м/с капли дождя? Массу капли принять
равной 0,1 г. (Ответ округли до целых.)
2. Найти период колебаний в контуре, емкость конденсатора в котором 5
мкФ, индуктивность катушки 3 мГн.
3. Колебательный контур состоит из конденсатора емкостью С=4,9мкФ и
катушки индуктивностью L=1 Гн. Амплитуда колебаний заряда на
обкладках конденсатора 0,5 мкКл. Напишите уравнение колебаний
заряда
4. Колебательный контур имеет индуктивность L=1,6 мГн и
электроемкость
С=0,04 мкФ, максимальное напряжение на
конденсаторе Um=200 В.
Определите максимальную силу тока в
контуре.
5. Как изменится циклическая частота, если в колебательном контуре
заменят конденсатор на другой меньшей в 36 раз емкостью?

10. Использованные ссылки

ИСПОЛЬЗОВАННЫЕ ССЫЛКИ
1. https://ykl-res.azureedge.net/81b14779-3f48-4e8e-bc83-c72cb4a19056/2-1.svg
2. https://www.yaklass.ru/p/fizika/9-klass/elektromagnitnoe-pole535026/kondensator-kolebatelnyi-kontur-printcipy-radiosviazi-i-televideniia534819/re-bc216da2-b62f-4649-a2be254bb20d7cca/pe?resultId=3723628861&c=1
3. https://upload.wikimedia.org/wikipedia/commons/thumb/b/b6/Jjthomson2.jpg/800px-Jj-thomson2.jpg

11. Скачано с www.znanio.ru

СКАЧАНО С WWW.ZNANIO.RU