Практика 5 _ Закон распределения двух дискретных случайных величин

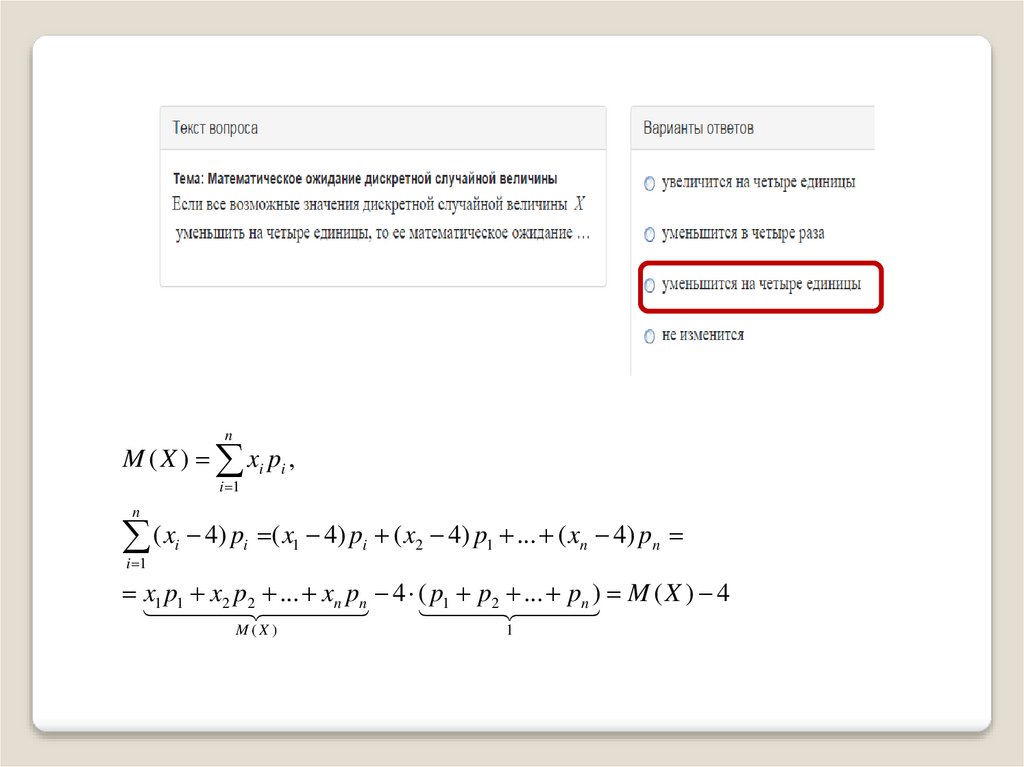
1. Закон распределения двух дискретных случайных величин

Практика

2.

n
M ( X ) xi pi ,
i 1
n
( x 4) p ( x 4) p ( x 4) p ... ( x 4) p
i 1
i
i
1
i
2
1
n
n
x1 p1 x2 p2 ... xn pn 4 ( p1 p2 ... pn ) M ( X ) 4
M (X )
1

3.

Суммой двух независимых дискретных случайных величин
Х и Y с законами распределения {(xi, pi)}, {(yj, qj)} называется
дискретная случайная величина U с законом распределения
{(xi + yj, pi ∙ qj )}. Обозначение: Х + Y.
Произведением
двух независимых дискретных случайных
величин Х и Y называется дискретная случайная величина V с
законом распределения
{( xi yj, pi qj )}. Обозначение: ХY.

4.

Задача
Заданы независимые случайные величины Х и Y:
xi
1
1
yj
0
1
2
3
pi
0,2 0,5 0,3
qj
0,2
0,4
0,3
0,1
Составить законы
Х2+Y2.
0
распределения случайных величин Х+Y, Х∙Y,
Решение
Закон распределения случайной величины Х+Y:
Возможны 6 значений произведений xi+yj: -1, 0, 1, 2, 3, 4.
p(Х+Y =-1)= p(X= 1, Y=0)=p(X= 1)·p(Y=0)=0,2·0,2=0,04;
p(Х+Y =0)= p(X=-1, Y=1) или p(X=0, Y=0)=0,2·0,4+ 0,5·0,2 =0,18;
p(Х+Y =1)=p(X=-1, Y=2) или p(X=0, Y=1) или p(X=1,Y=0)=0,2·0,3+
0,5·0,4 +0,3·0,2=0,32;
p(Х+Y =2)= p(X=-1, Y=3) или p(X=0, Y=2) или p(X=1,Y=1)=
0,2·0,1+0,5·0,3+0,3·0,4=0,29;
p(Х+Y =3)=p(X=0,Y=3) или р(X=1,Y=2) =0,5·0,1+0,3·0,3=0,14;
p(Х+Y =4)= p(X=1,Y=3) =0,3·0,1=0,03;
xi + yj
pij
1
0,04
0
0,18
1
0,32
2
0,29
3
0,14
4
0,03
Для контроля: 0,04+0,18+0,32+0,29+0,14+0,03=1

5.

Закон распределения случайной величины ХY.
xi
1
1
yj
0
1
2
3
pi
0,2 0,5 0,3
qj
0,2
0,4
0,3
0,1
0
Возможны 7 значений произведений xi·yj: 1, 2, 3, 0, 1, 2, 3.
Вероятности этих значений таковы:
p(XY= 3)=p(X= 1, Y=3)=p(X= 1)·p(Y=3)=0,2·0,1=0,02;
p(XY= 2)=p(X= 1, Y=2)=0,2·0,3=0,06;
p(XY= 1)=p(X= 1, Y=1)=0,2·0,4=0,08;
p(XY=0)=p(X=0 или Y=0)=p(X=0)+p(Y=0)–p(X=0) p(Y=0)=
=0,5+0,2–0,5·0,2=0,6;
p(XY=1)=p(X=1) p(Y=1)=0,3·0,4=0,12;
p(XY=2)=p(X=1) p(Y=2)=0,3·0,3=0,09;
p(XY=3)=p(X=1) p(Y=3)=0,3·0,1=0,03;
x iy j
pij
3
0,02
2
0,06
1
0,08
0
0,6
1
0,12
2
0,09
3
0,03
Для контроля: 0,02 + 0,06 + 0,08 + 0,6 + 0,12 + 0,09 + 0,03 = 1.

6.

Закон распределения случайной величины Х2+Y2:
xi
1
0
1
yj
0
1
2
3
xi2
1
0
1
yj2
0
1
4
9
pi
0,2 0,5 0,3
qj
0,2
0,4
0,3
0,1
Возможны 7 значений произведений xi2·yj2: 0, 1, 2, 4, 5, 9, 10.
p(Х2+Y2=0)=p(X=0 и Y=0)=0,5 0,2=0,1;
p(Х2+Y2=1)=p(X= 1 и Y=0) или p(X=0 и Y=1) или p(X=1 иY=0) =0,2 0,2+
+0,5 0,4+0,3 0,2 =0,04+0,2+0,06=0,3;
p(Х2+Y2=2)= p(X= 1, Y=1) или p(X=1, Y=1)=0,2 0,4+0,3 0,4=0,08+0,12=0,2;
p(Х2+Y2=4)=p(X=0, Y=2)=0,5 0,3=0,15;
p(Х2+Y2=5)=p(X= 1 и Y=2) или p(X=1 и Y=2)=0,2·0,3+0,3·0,3=0,15;
p(Х2+Y2=9)= p(X=0, Y=3)=0,5 0,1=0,05;
p(Х2+Y2=10)=p(X=-1, Y=3) или p(X=1, Y=3)=0,2 0,1+0,3 0,1=0,02+0,03=0,05.
xi2 y 2j
0
1
2
4
5
9
10
pij
0,1
0,3
0,2
0,15
0,15
0,05
0,05
Для контроля: 0,1+0,3+0,2+0,15+0,15+0,05+0,05=1

7.

Функции двух дискретных случайных величин
Пусть Х и Y две дискретные случайные величины с законами
распределения {(xi, pi)} и {(yj, qj)};
φ(х,у)
–
числовая
функция
двух
числовых
аргументов,
определенная для всех пар (xi, yj).
Дискретная случайная величина Z с законами распределения
{φ(хi, уj), pij}, где pij – вероятность события {X= xi, Y=yj},
называется функцией двух случайных величин Х и Y.
Аналогично вводится определение функции любого числа случайных
величин.
Если дискретные случайные величины Х и Y независимые, тогда
вероятность pij равна произведению pi·qj для всех пар индексов (i, j).

8.

Закон распределения двух дискретных случайных величин
Пусть Х и Y две дискретные случайные величины.
Например: Бросаем 2 игральных кубика, где мы Х случайная
величина –количество очков, выпавших в результате броска на первом
кубике.
Мы получаем следующий закон распределения вероятностей:
x
p(x)
1
1/6
2
1/6
3
1/6
4
1/6
5
1/6
6
1/6
Теперь рассмотрим другой такой же кубик и случайную величину Y –
количество очков, выпавших на втором кубике.
Очевидно, что вероятности выпадения его граней будут точно такими же:
у
q(у)
1
1/6
2
1/6
3
1/6
4
1/6
5
1/6
6
1/6
Получили законами распределения {(xi, pi)} и {(yj, qj)};
φ(х, у) – числовая функция двух числовых аргументов, определенная для
всех пар (xi, уj).
Построим закон распределения вероятностей системы (Х,Y).
Так как результат броска одного кубика никак не влияет на
количество очков, выпавших на другом кубике, то случайные величины X
и Y являются независимыми.

9.

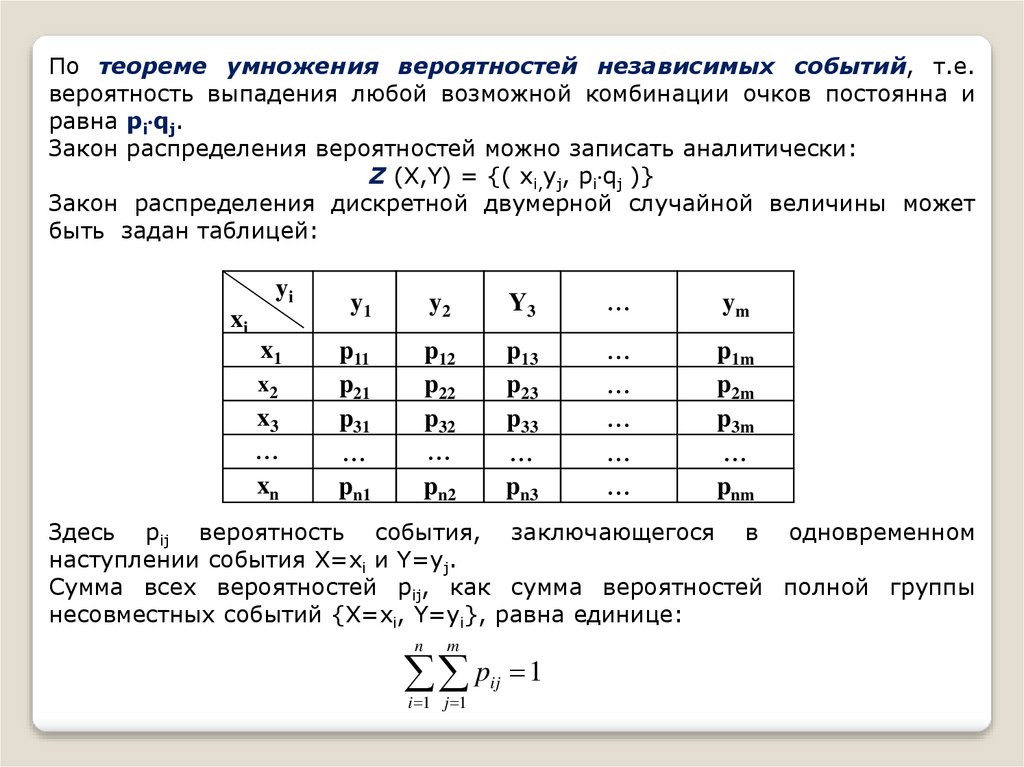
По теореме умножения вероятностей независимых событий, т.е.
вероятность выпадения любой возможной комбинации очков постоянна и
равна pi qj.
Закон распределения вероятностей можно записать аналитически:
Z (X,Y) = {( xi,yj, pi qj )}
Закон распределения дискретной двумерной случайной величины может
быть задан таблицей:
yi
xi
x1
x2
x3
…
xn
y1
y2
Y3
…
ym
p11
p21
p31
…
pn1
p12
p22
p32
…
pn2
p13
p23
p33
…
pn3
…
…
…
…
…
p1m
p2m
p3m
…
pnm
Здесь pij вероятность события, заключающегося в одновременном
наступлении события Х=хi и Y=yj.
Сумма всех вероятностей pij, как сумма вероятностей полной группы
несовместных событий {Х=xi, Y=yi}, равна единице:
n
m
p 1
i 1 j 1
ij

10.

В нашем примере:
yi
xi
1
2
3
4
5
6
1
2
3
4
5
6
1/36
1/36
1/36
1/36
1/36
1/36
1/36
1/36
1/36
1/36
1/36
1/36
1/36
1/36
1/36
1/36
1/36
1/36
1/36
1/36
1/36
1/36
1/36
1/36
1/36
1/36
1/36
1/36
1/36
1/36
1/36
1/36
1/36
1/36
1/36
1/36
n
m
p (1 / 36) 36 1
i 1 j 1
ij

11.

Задача
Заданы независимые случайные величины Х и Y.
xi
x1
x4
yj
y1
y2
y3
y4
pi
0,2 0,4 0,3 0,1
qj
0,2
0,4
0,3
0,1
Составить законы
x2
x3
распределения
Z(Х,Y).
Решение
Указанные законы распределения приведены в таблицах:
yi
xi
x1
x2
x3
xn
y1
y2
y3
y4
0,04
0,08
0,06
0,02
0,08
0,16
0,12
0,04
0,06
0,12
0,09
0,03
0,02
0,04
0,03
0,01

12.

Задача
Игральную кость бросают два раза. Определим случайную
величину Х как число выпавших шестерок. Случайная величина Y
будет принимать значение 0, если хотя бы на одной кости
выпадает нечетное число, и 1, если на обоих костях выпадает
четное. Выпишем таблицу совместного распределения случайной
величин X и Y.
Решение
Случайная величина Х принимает три значения {0;1;2},
а
случайная величина Y принимает два значения {0;1}.
Следовательно, таблица совместного распределения будет иметь
вид:
yi
xi
0
1
0
1
2
Вычислим соответствующие вероятности.

13.

yi
0
1
0
21/36
1
6/36
0
4/36
4/36
1/36
xi
2
Вычислим р32=Р(Х=2, Y=1)=1/36.
р31=Р(Х=2, Y=0)=0 т.к. такой исход не возможен.
р22=Р(Х=1, Y=1)
Этому событию соответствует 4 элементарных исхода:
{6,2}, {6,4}, {2,6}, {4,6}.
р22=Р(Х=1, Y=1)=4/36.
р21=Р(Х=1, Y=0)
Этому событию соответствует 6 элементарных исходов:
{6,1}, {6,3}, {6,5}, {1,6} ,{3,6}, {5,6}.
р22=Р(Х=1, Y=1)=6/36.
р12=Р(Х=0, Y=1)
Этому событию соответствует 4 элементарных исхода:
{2,2}, {2,4}, {4,2}, {4,4}.
р22=Р(Х=1, Y=1)=4/36.
р11=Р(Х=0, Y=0) можно вычислить так
р11=1- р12-р21-р22-р31-р32=1-4/36-6/36-4/36-0-1/36=21/36

14.

Маргинальные (частные) распределения
Из таблицы совместного распределения двух дискретных величин
можно получить распределение каждой случайной величин X и Y.
Такие распределения называются маргинальными или частными.
Для того чтобы получить такое распределение для Х, найти
вероятность Р(Х=xi), надо просуммировать вероятности в i-ой
строке таблицы совместного распределения:
Р(Х=xi)=pi1+pi2+…+pim.
Для того чтобы получить такое распределение для Y, найти
вероятность Р(Y=yj), надо просуммировать вероятности в j-ом
столбце таблицы совместного распределения:
Р(Y=yj)=p1j+p2j+…+pnj.
Рассмотрим совместное распределение из предыдущего примера
Маргинальное распределение для X
yi
0
1
и Y задаются таблицами:
xi
xi
0
1
2
0
21/36 4/36
25/36 10/36 1/36
р
1
2
6/36
0
4/36
1/36
yi
р
0
27/36
1
9/36

15.

Теорема
Дискретная случайная величина Х и У независимы тогда и только тогда, когда для
любых i и j, i=1,…, n , j =1,…, m
Pij=P(X=xi, Y=yi) = P(X=xi) P(Y=yi).
Эту формулу можно использовать для проверки независимости двух декретных
случайных величин.
Маргинальные распределения:
Например: P(X = 0) = 25/36 и P(Y = 0) = 27/36.
Проверим выполнение условий независимости: P(X = 0,Y = 0) =
P(X = 0) · P(Y = 0) 21/36= 25/36 · 27/36.
Следовательно, X и Y зависят друг от друга.

16.

Определение
Распределение одной случайной величины, входящей в систему,
найденное при условии, что другая случайная величина приняла
определенное
значение,
называется
условным
законом
распределения.
Если двумерная случайная величина задана таблицей совместного
распределения, то условные вероятности составляющих Х и У
вычисляют по формулам:
p( X / Y )
Р( хi / yi )
Р( yi / xi )
p( X Y )
P(Y )
pij
p ( yi )
pij
p( xi )
Значение рij, берут из таблицы совместного распределения.
m
p( х / y ) 1,
i 1
i
i
n
p( y / x ) 1.
j 1
i
i

17.

Задача
Закон распределения системы (Х, Y) задан таблицей:
yj
xi
1
0
1
1
0
1
3
0,1
0,05
0,1
0,2
0,1
0,05
0
0,05
0,15
0,1
0
0,1
Найти:
а) законы распределения случайных величин Х и Y в отдельности;
б) закон распределения Х при условии, что Y = 1;
в) вероятность события {Х< 1, Y 1}.
Решение
p( X 1) p1 p11 p12 p13 p14 0,4;
p( X 0) p2 p21 p22 p23 p24 0,2;
p( X 1) p3 p31 p32 p33 p34 0,4;
Законы распределения случайных величин Х:
xi
pi
1
0,4
0
0,2
1
0,4

18.

yj
xi
1
0
1
1
0
1
3
0,1
0,05
0,1
0,2
0,1
0,05
0
0,05
0,15
0,1
0
0,1
p(Y 1) q1 p11 p21 p31 0,25;
p(Y 0) q2 p12 p22 p32 0,35;
p(Y 1) q3 p13 p23 p33 0,2;
p(Y 3) q4 p14 p24 p34 0,2.
Законы распределения случайных величин Y:
yj
qj
1
0,25
0
0,35
1
0,2
3
0,2

19.

б) закон распределения Х при условии, что Y = 1;
yj
xi
1
0
1
1
0
1
3
0,1
0,05
0,1
0,2
0,1
0,05
0
0,05
0,15
0,1
0
0,1
p( X / Y )
p( X Y )
P(Y )
xi
pi
1
0,4
0
0,2
yj
qj
1
0,25
0
0,35
1
0,4
1
0,2
p( X 1 / Y 1) p13 / q3 0 / 0,2 0
p( X 0 / Y 1) p23 / q3 0,05 / 0,2 0,25
p( X 1 / Y 1) p33 / q3 0,15 / 0,2 0,75
Закон распределения случайной величины Х при условии, что
Y =1:
xi -1
0
1
pi
0
0,25 0,75
3
0,2

20.

в) вероятность события {Х< 1, Y 1}
yj
xi
1
0
1
1
0
1
3
0,1
0,05
0,1
0,2
0,1
0,05
0
0,05
0,15
0,1
0
0,1
р(Х < 1, Y 1) = 0+0,1 + 0,05+0 = 0,15.

21.

Задача
Две независимые случайные величины Х и Y имеют такие законы
распределения:
xi
pi
0
0,3
1
0,2
2
0,1
3
0,4
1
0,2
yj
qj
3
0,1
4
0,7
Построить закон распределения случайной величины Z = min(X,Y).
Решение
Для удобства составления закона распределения случайной
величины Z представим ее возможные значения числа zij и
вероятности этих значений произведения в таблицах:
pij = pi qj
Z = min(xi, yj)
yj
xi
0
1
2
3
1
3
4
1
1
1
1
0
1
2
3
0
1
2
3
qj
pi
0,3
0,2
0,1
0,4
0,2
0,1
0,7
0,06
0,04
0,02
0,08
0,03
0,02
0,01
0,04
0,21
0,14
0,07
0,28
Закон распределения случайной величины Z:
zi
pi
1
0,2
0
0,24
1
0,16
Для контроля: 0,2 0,24 0,16 0,08 0,32 1
2
0,08
3
0,32

22.

Числовые характеристики системы дискретных случайных величин
Числовые характеристики случайных величины Х и Y находятся по
следующим правилам:
m
n
m
M ( X ) xi pij a x ,
M (Y ) yi pij a y
j 1 i 1
m
n
j 1 i 1
n
D( X ) ( xi a x ) pij ,
2
j 1 i 1
m
n
D(Y ) ( yi a y ) 2 pij .
j 1 i 1
Пример: Найти числовые характеристики случайных величины Х и Y
yj
xi
m
1
0
1
1
0
1
3
0,1
0,05
0,1
0,2
0,1
0,05
0
0,05
0,15
0,1
0
0,1
n
M ( X ) xi pij ( 1 (0,1 0,2 0 0,1) 0 (0,05 0,1 0,05 0) 1 (0,1 0,05 0,15 0,1) 0,4 0,4 0 а х ,
j 1 i 1
m
n
M (Y ) yi pij ( 1 (0,1 0,05 0,1) 0 (0,2 0,1 0,05) 1 (0 0,05 0,15) 3 (0,1 0 0,1) 0,55 a y
j 1 i 1
m
n
D( X ) ( xi a x ) 2 pij ( 1) 2 (0,1 0,2 0 0,1) 12 (0,1 0,05 0,15 0,1) 0,8,
j 1 i 1
m
n
D(Y ) ( yi a y ) 2 pij ( 1 0,55) 2 (0,1 0,05 0,1) (0 0,55) 2 (0,2 0,1 0,05) (1 0,55) 2 (0 0,05 0,15)
j 1 i 1
(3 0,55) 2 (0,1 0 0,1) 1,9475.

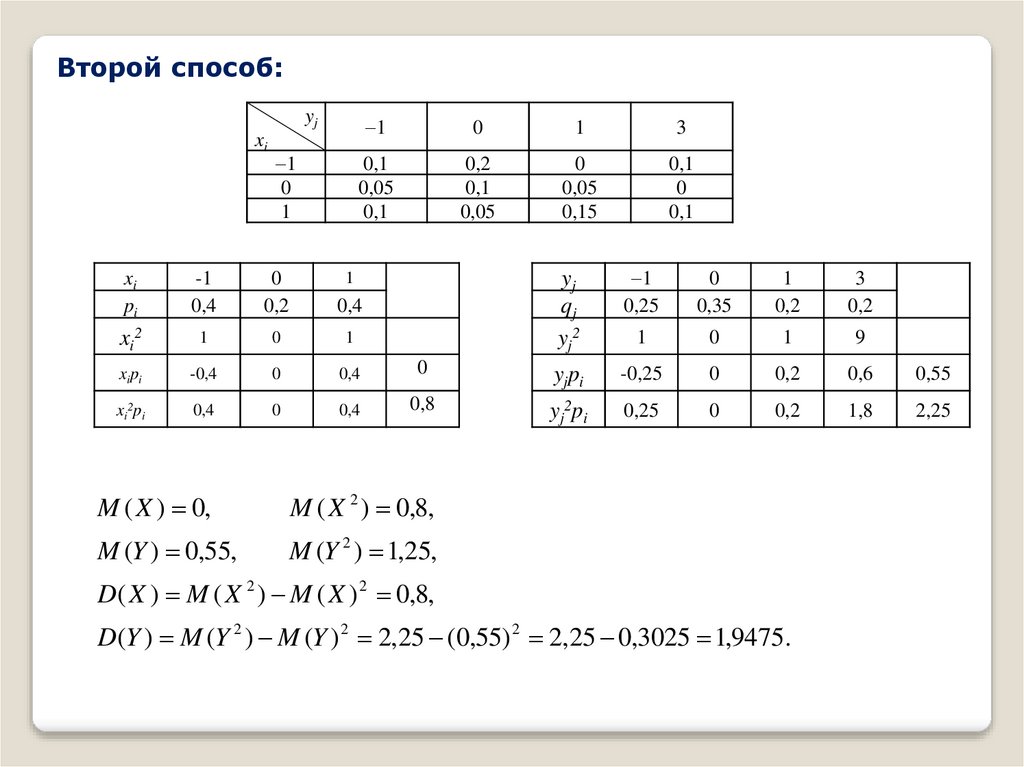
23.

Второй способ:
yj
xi
1
0
1
1
0
1
3
0,1
0,05
0,1
0,2
0,1
0,05
0
0,05
0,15
0,1
0
0,1
xi
pi
-1
0,4
0
0,2
0,4
xi2
1
0
1
xipi
-0,4
0
0,4
xi2pi
0,4
0
0,4
yj
qj
yj2
1
0,25
0
0,35
1
0,2
3
0,2
1
0
1
9
0
yjpi
-0,25
0
0,2
0,6
0,55
0,8
yj2pi
0,25
0
0,2
1,8
2,25
1
M ( X ) 0,
M ( X 2 ) 0,8,
M (Y ) 0,55,
M (Y 2 ) 1,25,
D( X ) M ( X 2 ) M ( X ) 2 0,8,
D(Y ) M (Y 2 ) M (Y ) 2 2,25 (0,55) 2 2,25 0,3025 1,9475.

24.

√

25.

Задача для самостоятельной работы
Ниже для каждой пары значений (xi, yj) дискретных случайных
величин Х и Y заданы вероятности pij:
yj
xi
1
0
1
0
1
2
3
0,01
0,04
0,05
0,06
0,24
0,10
0,05
0,15
0,10
0,04
0,07
0,09
Найти:
1. закон распределения суммы Z =Х+Y.
2. закон распределения Х при условии, что Y = 2;
3. вероятность события {Х< 1, Y 2}.
4. числовые характеристики случайных величины Х и Y
xi
pi
-1
0,16
0
0,5
1
0,34
yj
qj
0
0,1
1
0,4
2
0,3
3
0,2