Урок 4. Независимость событий" 2

1. Независимые собы­тия.

Независимые события.

2.

Бывают события, которые не зависят друг от друга. Например, при
бросании двух костей результат бросания первой кости не влияет
на число очков, выпавших на второй кости. Про такие события
говорят, что они независимы.
Разумно считать, что события А и В независимы, если наступление
одного из них не влияет на вероятность другого.
Если вероятности событий А и В больше нуля, то независимость
событий А и В можно выразить равенствами
Р(А|В) = Р(А) и Р(В|А) = Р(В).
Но тогда из известных нам формул получается равенство
Р(А В) = Р(А) Р(В).
Определение. Два события А и В называются независимыми, если
вероятность их пересечения равна произведению их вероятностей:
Р(А В) = Р(А) Р(В).

3. Пример 1

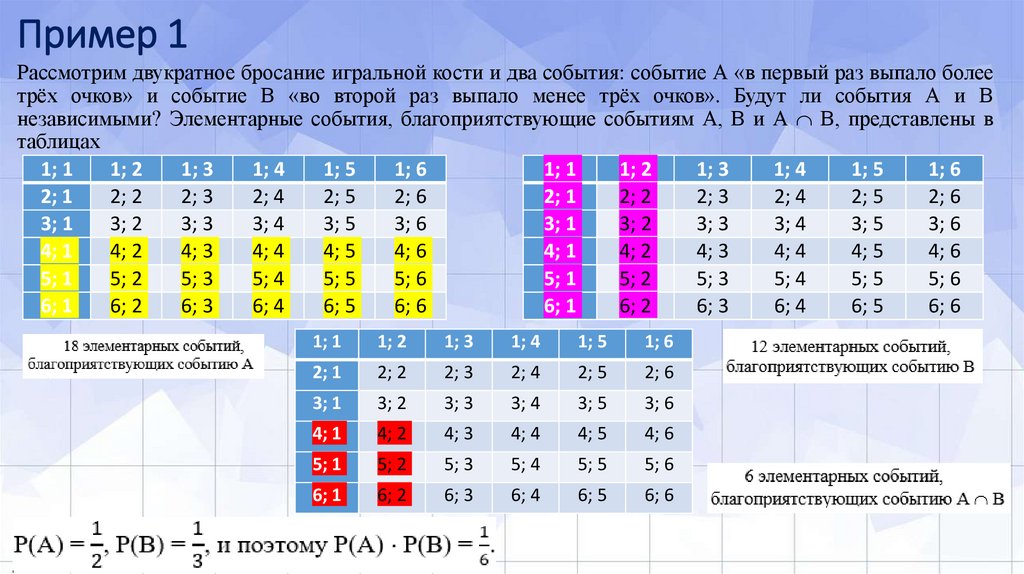
Рассмотрим двукратное бросание игральной кости и два события: событие А «в первый раз выпало более
трёх очков» и событие В «во второй раз выпало менее трёх очков». Будут ли события А и В
независимыми? Элементарные события, благоприятствующие событиям А, В и А В, представлены в
таблицах
1; 1
1; 2
1; 3
1; 4
1; 5
1; 6
1; 1
1; 2
1; 3
1; 4
1; 5
1; 6
2; 1
2; 2
2; 3
2; 4
2; 5
2; 6
2; 1
2; 2
2; 3
2; 4
2; 5
2; 6
3; 1
3; 2
3; 3
3; 4
3; 5
3; 6
3; 1
3; 2
3; 3
3; 4
3; 5
3; 6
4; 1
4; 2
4; 3
4; 4
4; 5
4; 6
4; 1
4; 2
4; 3
4; 4
4; 5
4; 6
5; 1
5; 2
5; 3
5; 4
5; 5
5; 6
5; 1
5; 2
5; 3
5; 4
5; 5
5; 6
6; 1
6; 2
6; 3
6; 4
6; 5
6; 6
6; 1
6; 2
6; 3
6; 4
6; 5
6; 6
1; 1
1; 2
1; 3
1; 4
1; 5
1; 6
2; 1
2; 2
2; 3
2; 4
2; 5
2; 6
3; 1
3; 2
3; 3
3; 4
3; 5
3; 6
4; 1
4; 2
4; 3
4; 4
4; 5
4; 6
5; 1
5; 2
5; 3
5; 4
5; 5
5; 6
6; 1
6; 2
6; 3
6; 4
6; 5
6; 6

4. Пример 2

Наудачу выбираем число из ряда 1, 2, 3, 4, ..., 100. Пусть событие А состоит в том, что
это число чётное; событие В – что это число делится на 5. Тогда событие А В состоит в
том, что выбранное число делится и на 2, и на 5. Это значит, что выбранное число
делится на 10.
Покажем, что события А и В независимы. Нужно найти вероятности Р(А), Р(В), Р(А В)
и убедиться в том, что выполняется равенство
Р(А В) = Р(А) Р(В),
50
Среди 100 первых натуральных чисел всего 100 : 2 = 50 чётных. Поэтому Р(А) =
=
100
0,5.
Среди 100 первых натуральных чисел
на 5 делятся числа 5, 10, 15, 20, …, 95, 100 – всего
20
100 : 5 = 20 чисел. Поэтому Р(В) =
= 0,2.
100
Среди первых 100 натуральных чисел всего 100 : 10 = 10 чисел, кратных 10.
Следовательно,
10
Р(А В) =
= 0,1.
100
Таким образом, Р(А В) = 0,1 и Р(А) Р(В) = 0,5 0,2 = 0,1.
Получаем, что Р(А В) = Р(А) Р(В).
Следовательно, события А и В независимы.

5.

Пример 3

6. Пример 4

Два стрелка делают по одному выстрелу в мишень. Вероятность попадания для первого — 0,6,
для второго — 0,8. Чему равны вероятности следующих событий:
C = «оба стрелка попадут в мишень»;
D = «хотя бы один из них попадёт»;
E = «оба стрелка промахнутся»;
F = «хотя бы один из них промахнётся»?
Решение
1. Из условий нашего опыта следует, что события A и B можно считать независимыми: каждый из
стрелков не может повлиять своим выстрелом на результат другого. Поэтому вероятность
события C можно вычислить по правилу умножения для независимых событий:
P(C) = P(A B) = P(A) · P(B) = 0,6 · 0,8 = 0,48.
2. Событие D является объединением событий A и B, поэтому для вычисления вероятности P(D)
нужно использовать правило суммы. При этом события A и B могут произойти одновременно, т. е.
пересекаются, поэтому используем правило суммы для пересекающихся (совместных)
событий:
P(D) = P(A B) = P(A) + P(B) – P(A B) = 0,6 + 0,8 – 0,48 = 0,92.
Или: P(D) = Р(А)*Р(В) + Р(А)*Р(В) + Р(А)*Р(В) = 0,6*(1-0,8) +(1-0,6)*0,8+0,6*0,8 = 0,92

7. Пример 4 (продолжение)

E = «оба стрелка промахнутся»
F = «хотя бы один из них промахнётся»?
Решение
3. Вероятность события E можно найти двумя способами.
P(E) = P(А В) = P(А) · P(В ) = (1 – P(A))(1 – P(B)) = 0,4 · 0,2 = 0,08.
Или: E =