Независимые события. Умножение вероятностей

1. НЕЗАВИСИМЫЕ СОБЫТИЯ. УМНОЖЕНИЕ ВЕРОЯТНОСТЕЙ.

8 класс

2. Цели урока:

1. Ввести понятие независимых событий, опираясь на
жизненный опыт учеников;
2. Научить видеть независимые события в окружающем
мире;
3. Ввести формулу умножения вероятностей.
Задачи урока:
1. Воспитывать
у
учащихся
организованность,
уверенность в своих знаниях;
2. Способствовать развитию наблюдательности, умению
анализировать и делать выводы;
3. Побуждать учащихся к взаимоконтролю,
вызывать у них потребность в обоснованиисвоих высказываний.
Конспект урока

3.

!
ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ
стр. 132 № 5
ДАНО:
К={встреча с черной кошкой} P(К)=0,1
К
С
К∩С
С={ встреча со злой собакой} P(C)=0,4
Вероятность того, что вам встретится
и черная кошка и злая собака
P(К∩С)=0,04
РЕШЕНИЕ:
а) Вероятность того, что вам встретится хотя бы одно из
этих животных:
P(К∪С)= P(К)+P(C) - P(К∩С)= 0,1+0,4-0,04=0,46
б) Вероятность того, что вы не
встретите ни черную кошку, ни злую
собаку: P(К∪С)=1- P(К∪С)=0,54
ОТВЕТ: а) 0,46; б)0,54.

4.

!
ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ стр. 132 № 6
ДАНО:
P(А)=0,1
А={вызов к доске на 1 уроке}
А
А∩В
В
РЕШЕНИЕ:
P(В)=0,3
В={вызов к доске на 2 уроке}
Вероятность того, что вас вызовут и на
первом и на втором уроках, то есть
P(А∩В)=0,03
а) Вероятность того, что вас вызовут хотя бы на одном из
двух уроков:
P(А∪В)= P(А)+P(В) - P(А∩В)= 0,1+0,3-0,03=0,37
б) Вероятность того, что вас не вызовут ни
на одном из двух уроков:
P(А∪В)=1- P(А∪В)=0,63
ОТВЕТ: а) 0,37; б)0,63.

5.

СОБЫТИЯ
совместные
несовместные

6.

А={Алиса спит}
В={Алиса ест бутерброд}
события
несовместные
А={Алиса на даче }
В={Алиса ест бутерброд}
события совместные
{Алиса на даче ест бутерброд }

7.

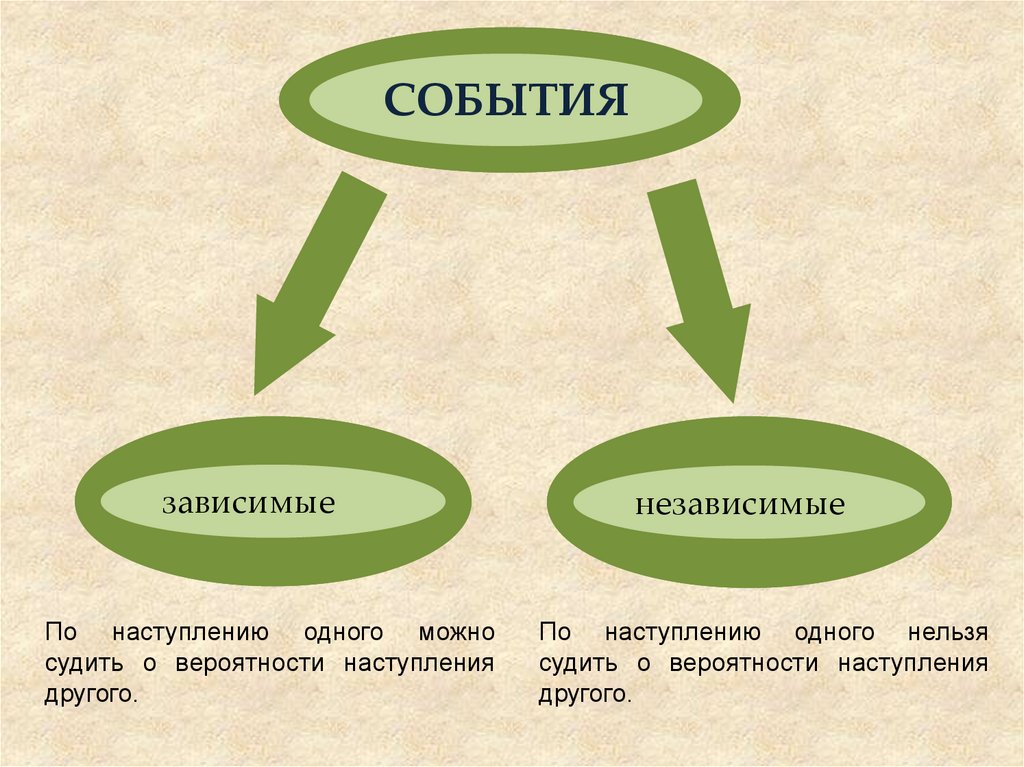
СОБЫТИЯ
зависимые
По наступлению одного можно
судить о вероятности наступления
другого.
независимые
По наступлению одного нельзя
судить о вероятности наступления
другого.

8.

Задание 1
Охарактеризуйте
события, о которых идет речь в
приведенных заданиях как зависимые и независимые.
ЗАВИСИМЫЕ:
А: я получил двойку;
В: мама будет ругаться.
А: на первой кости выпало 5 очков;
В: на второй кости выпало 3 очка.
НЕЗАВИСИМЫЕ:
А:гол забил Аршавин;
В: гол забил Павлюченко.
А: Оля пришла без сменной обуви;
В: Оля ходит в бахилах.

9.

В теории вероятностей
за определение
независимости событий взято выполнение
равенства:
События А и В называются независимыми,
если вероятность их пересечения равна
произведению их вероятностей.

10.

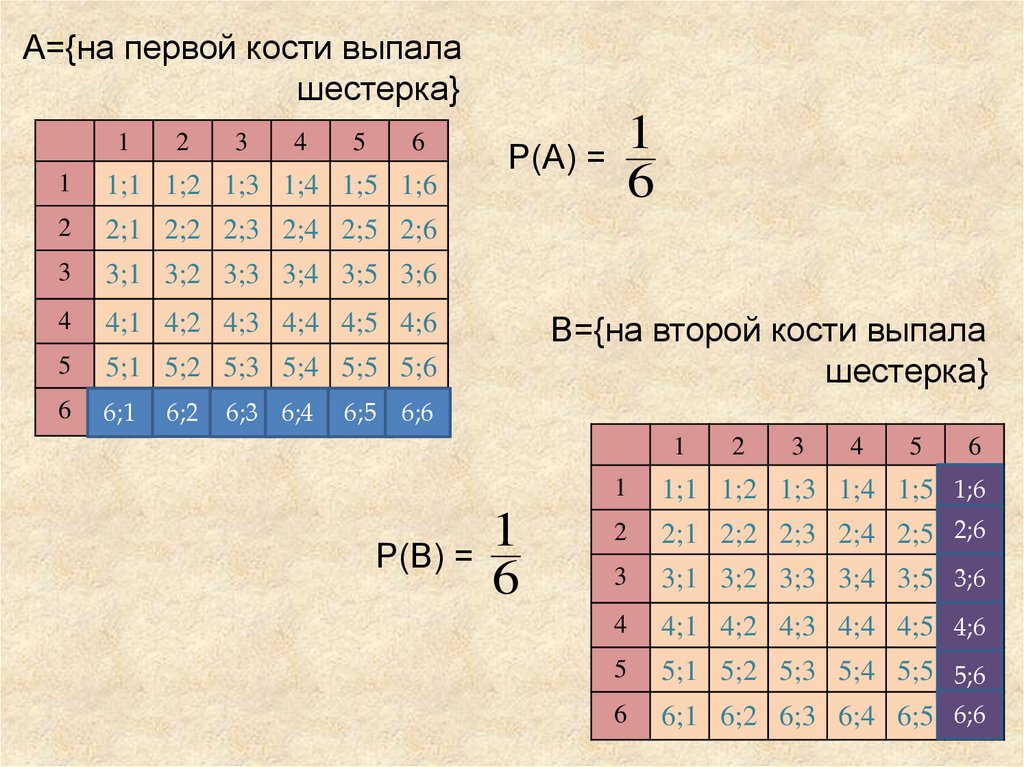
Чтобы пояснить формулу рассмотрим пример:
Бросаем две
игральные кости.
В
этом
опыте
36
элементарных событий,
записанных
в
виде
таблицы:

11.

А={на первой кости выпала
шестерка}
1
2
3
4
5
6
1
1;1 1;2 1;3 1;4 1;5 1;6
2
2;1 2;2 2;3 2;4 2;5 2;6
3
3;1 3;2 3;3 3;4 3;5 3;6
4
4;1 4;2 4;3 4;4 4;5 4;6
5
5;1 5;2 5;3 5;4 5;5 5;6
6
6;1 6;2 6;3 6;4
6;4 6;5
6;1
6;5 6;6
6;6
Р(А) =
1
6
В={на второй кости выпала
шестерка}
1
1
Р(В) =
6
2
3
4
5
6
1
1;1 1;2 1;3 1;4 1;5 1;6
1;6
2
2;1 2;2 2;3 2;4 2;5 2;6
2;6
3
3;1 3;2 3;3 3;4 3;5 3;6
3;6
4
4;1 4;2 4;3 4;4 4;5 4;6
4;6
5
5;1 5;2 5;3 5;4 5;5 5;6
5;6
6;1 6;2 6;3 6;4 6;5 6;6
6;6
6

12.

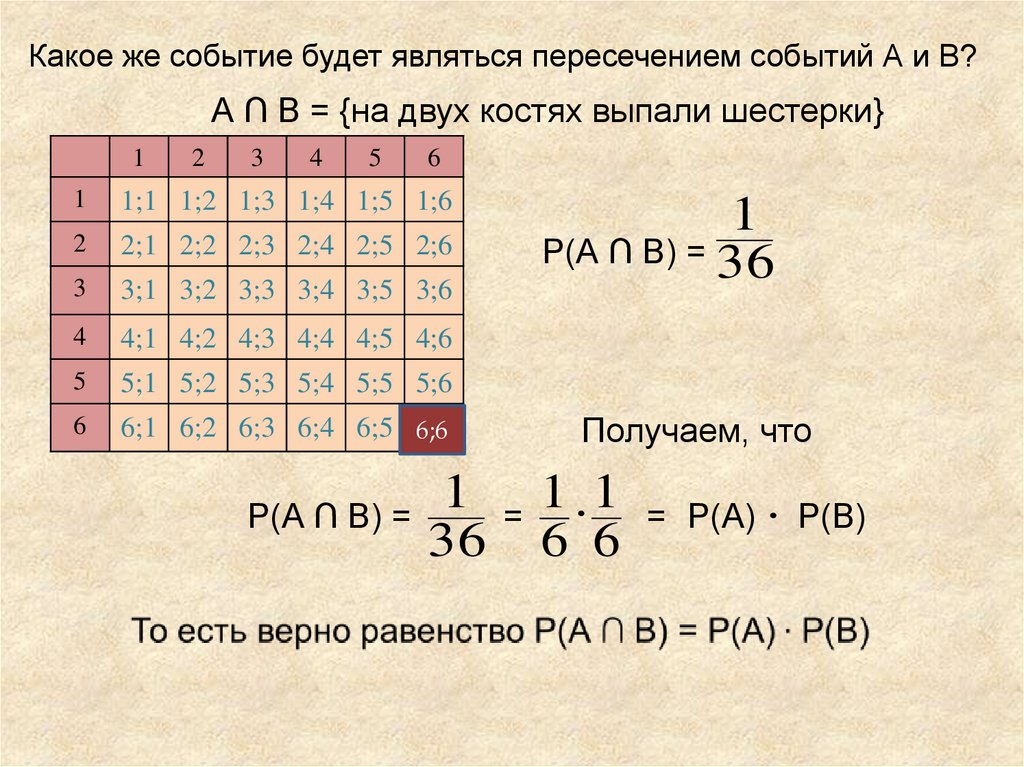
Какое же событие будет являться пересечением событий А и В?
А ∩ В = {на двух костях выпали шестерки}
1
2
3
4
5
6
1
1;1 1;2 1;3 1;4 1;5 1;6
2
2;1 2;2 2;3 2;4 2;5 2;6
3
3;1 3;2 3;3 3;4 3;5 3;6
4
4;1 4;2 4;3 4;4 4;5 4;6
5
5;1 5;2 5;3 5;4 5;5 5;6
6
6;1 6;2 6;3 6;4 6;5 6;6
6;6
Р(А ∩ В) =
1
Р(А ∩ В) = 36
Получаем, что
1 = 1 1 = Р(А) Р(В)
36 6 6

13.

Задание 2
События U и V независимы. Найдите вероятность
события U ∩ V, если Р(U) = 0,4, Р(V) = 0,6.
ОТВЕТ: 0,24.
Задание 3
События К и L независимы. Найдите вероятность
события K, если Р(L) = 0,2, Р(K ∩ L) = 0,08.
ОТВЕТ: 0,4.
Задание 4
События К, L и М независимы. Найдите вероятность
события K, если Р(L) = 0,8, Р(М) = 0,6, Р(K ∩ L ∩М) = 0,096.
ОТВЕТ: 0,2.

14.

Задание 5
Случайным образом выбираем натуральное число от 1 до
24. Событие С = {число четное}. Являются ли события С и
D независимыми, если событие D состоит в том, что
выбранное число делится на 3.
Задание 6
Из ящика где хранятся 9 желтых и 15 зеленых
карандашей, продавец, не глядя, вынимает один за
другим два карандаша. Найдите вероятность того, что
оба карандаша окажутся желтыми.

15.

Задание 7
Монету бросают три раза. Событие А = {первые два раза
выпал орел}. Событие В = {третий раз выпала решка}.
а) Выпишите все элементарные события этого случайного
эксперимента.
б) Сколько элементарных событий благоприятствует
событию А, и сколько – событию В?
в) Найдите вероятности событий А, В и А∩В.
г) Являются ли события независимыми?

16.

РЕШЕНИЕ:
а) ООО, ОРО, РОР, ООР, РОО, ОРР, РРО, РРР;
б) А: ООР, ООО, т.е. 2 эл. события;
В: ООР, ОРР, РРР, РОР, т.е. 4 эл. события
А ∩ В: ООР т.е. 1 эл. событие;

17.

1 вариант
Самостоятельная работа
2 вариант
1. События С и D независимы. Найдите Р(С ∩ D), если
Р(С) = 0,3; Р(D) = 0,5.
Р9С) = 0,2; Р(D) = 0,7.
2. События К и L независимы. Найдите Р(К), если
Р(L) = 0,9; Р(K ∩ L) = 0,72.
Р(L) = 0,7; Р(K ∩ L) = 0,56.
3. Монету бросают два раза:
А = {первый раз выпал орел}; А={первый раз выпала решка};
В={второй раз выпала решка}.
В = {второй раз выпал орел}.
Выпишите все элементарные события этого опыта. Являются
ли события независимыми?
4.* Из ящика, где хранятся 5 желтых и 7 красных шаров,
продавец, не глядя, вынимает один за другим три шара.
Найдите вероятность того, что
первые два будут желтыми, а
первые два будут красные, а
третий шар − красным.
третий шар − желтым.

18.

ДОМАШНЕЕ ЗАДАНИЕ
1) стр. 139 №1 (б)
2) стр.139 №2 (б)
3) стр.139 №4 (б,г)
4) стр.139 №6 (б)