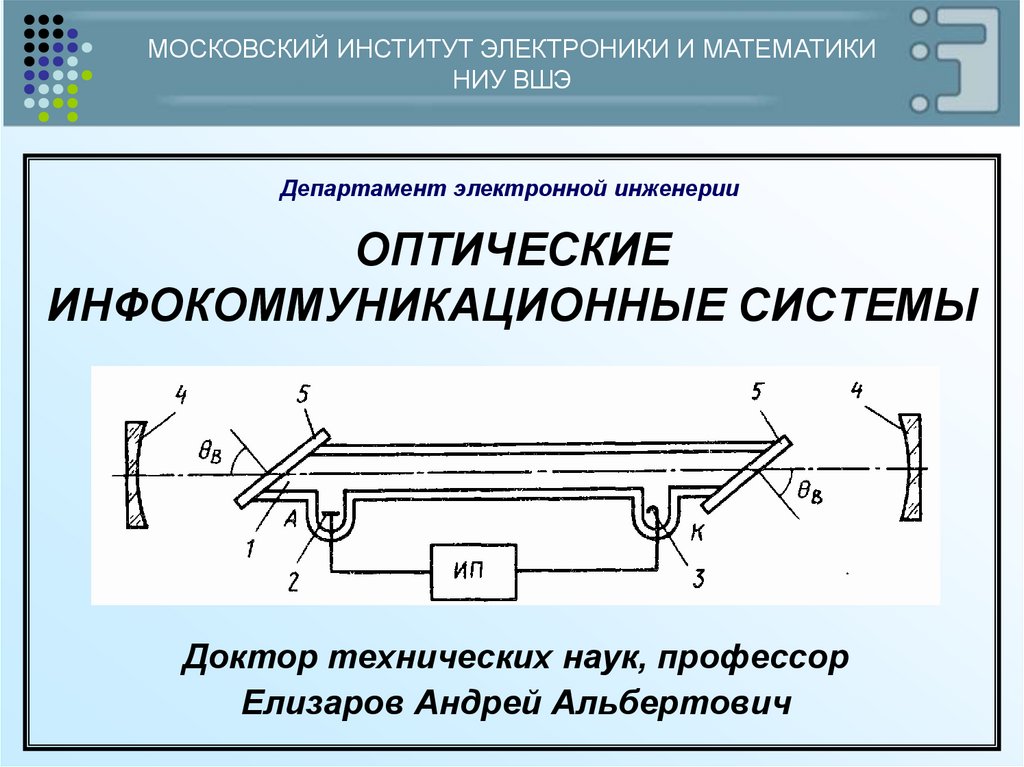
Оптические инфокоммуникационные системы

1.

МОСКОВСКИЙ ИНСТИТУТ ЭЛЕКТРОНИКИ И МАТЕМАТИКИ
НИУ ВШЭ
Департамент электронной инженерии
ОПТИЧЕСКИЕ
ИНФОКОММУНИКАЦИОННЫЕ СИСТЕМЫ
Доктор технических наук, профессор
Елизаров Андрей Альбертович

2.

Рекомендуемая литература :
1. Тарасов Л.В. Физические основы квантовой электроники. М. :
«Советское радио», 1976.
2. Тарасов Л.В. Физика процессов в генераторах когерентного
оптического излучения. М. : «Радио и связь», 1981.
3. Страховский Г.М., Успенский А.В. Основы квантовой
электроники. М., 1979.
4. Батраков А.С. Квантовые приборы. Л.: «Энергия», 1972.
5. Дьяков В.А. Введение в квантовую электронику. М.: «Энергия»,
1969.
6. Ищенко Е.Ф., Климков Ю.М. Оптические квантовые генераторы. М.
: «Советское радио», 1968.
7. Киселев Г.Л. Приборы квантовой электроники. М. : «Высшая
школа», 1980.
8. Пихтин А.Н. Оптическая и квантовая электроника. М.: «Высшая
школа», 2001.
9. Справочник по лазерам / под ред. Прохорова А.М. в 2-х т. М, 1978.
10. Тарасов Л.В. 14 лекций о лазерах. М.: Книжный дом «Либроком»,
2011.
11. Киселев Г.Л. Квантовая и оптическая электроника. Л.: «Лань»,
2011.

3.

Лекции № 1, 2
Физические основы взаимодействия
квантовых систем с
электромагнитным полем
Лазер (Light Amplification by Stimulated Emission of Radiation)
Мазер (Microwave Amplification by Stimulated Emission of Radiation)
Классификация квантовых приборов.
1. по спектральному диапазону работы:
если мм – лазеры (оптический диапазон);
если мм – мазеры (СВЧ диапазон).
2. по агрегатному состоянию рабочей среды:
1) газовые;
2) твердотельные лазеры или мазеры;
3) полупроводниковые;
4) жидкостные.

4.

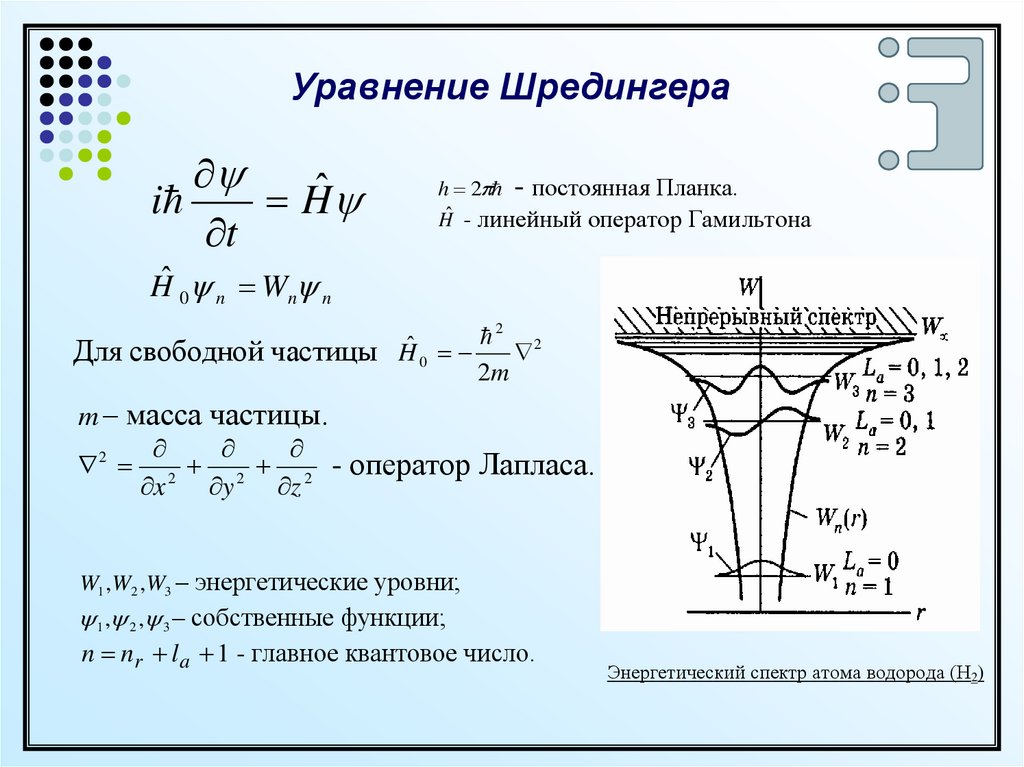
Уравнение Шредингера
i
Hˆ
t
h 2 - постоянная Планка.
Ĥ - линейный оператор Гамильтона
Hˆ 0 n Wn n
2
Для свободной частицы Hˆ 0 2
2m
m – масса частицы.
2 2 2 2 - оператор Лапласа.
x
y
z
W1 ,W2 ,W3 – энергетические уровни;
1 , 2 , 3 – собственные функции;
n nr la 1 - главное квантовое число.
Энергетический спектр атома водорода (Н2)

5.

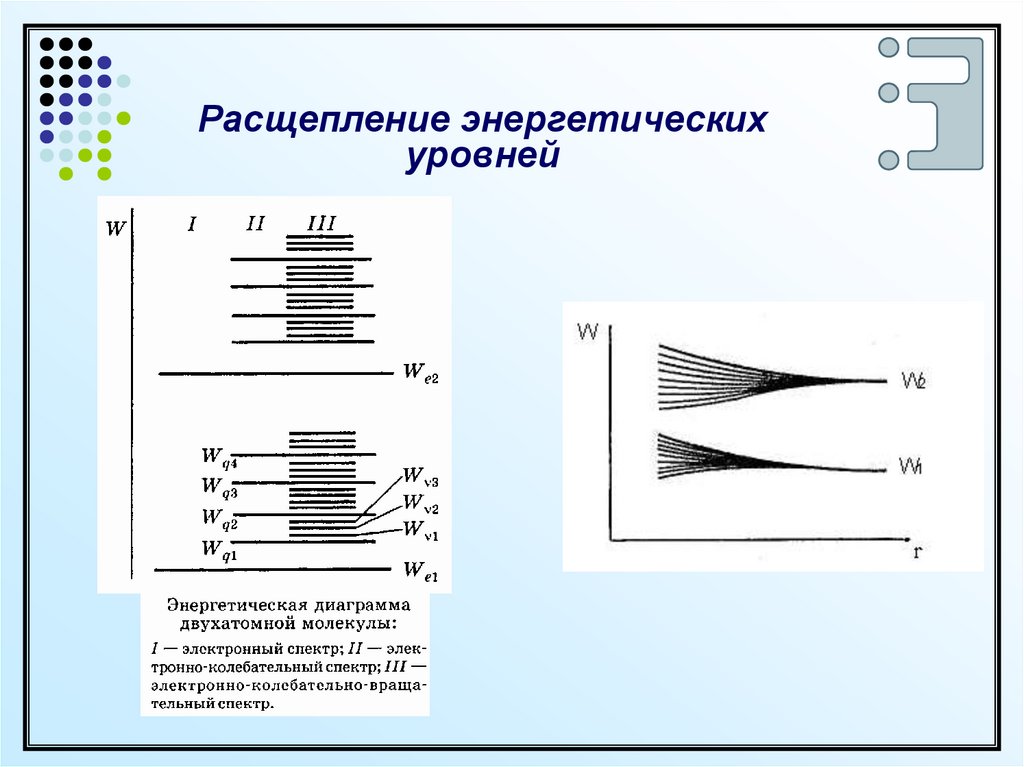
Расщепление энергетических
уровней

6.

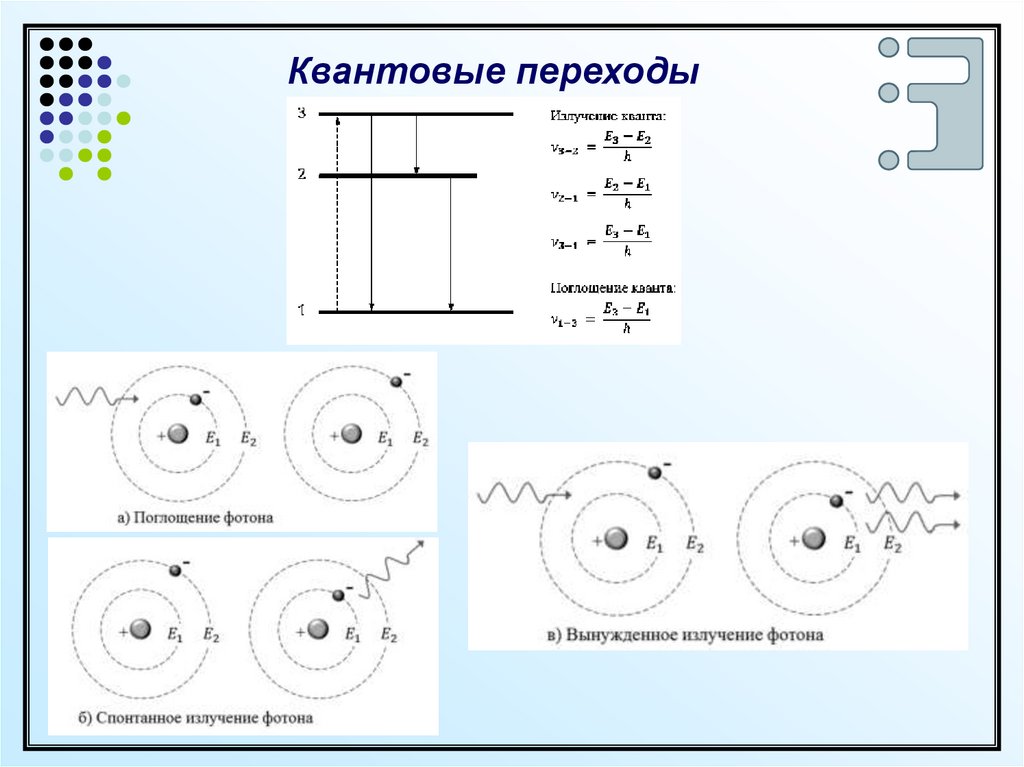
Квантовые переходы

7.

Квантовые переходы
Однофотонные квантовые переходы
W m Wn
- излучательный переход
mn
Wm Wn
Вероятность переходов под воздействием возмущений вычисляют в
соответствии с уравнением Шредингера.
d x ex - дипольный момент, где e - заряд электрона, x - смещение электрона
под действием электромагнитного поля.
Энергия взаимодействия: H E x dx
при z 0
E x E0 x exp i t exp i t
a mn
2
4e 2 X 2 mn 2 sin 2 0.5 mn t
E 0x
- вероятность перехода квантовой системы с
2
mn 2
излучением энергии.
mn
Wm Wn
- частота гармонического возмущения

8.

Коэффициенты Эйнштейна
a mn
2
4e 2 X 2 mn 2 sin 2 0.5 mn t
E 0x
- вероятность перехода квантовой системы с
2
mn 2
поглощением энергии.
a mn
2
P ( ) 2 3
c
2
~ E2
- закон излучения Планка
exp
1
kT
Среднее значение энергии излучения в единице объема P 2 E 2 0 x
Для всего интервала частот:
amn
2
sin 2 ( mn )t
2 2
*
e
X
X
P
(
)
d
mn
mn
0
mn
2
при P( ) const
a mn
2 2
e X mn X * mn tP( )
2
X mn X * ~ 0.33rmn r * mn
2
2 2
e rmn r * mn - коэффициент Эйнштейна для индуцированного излучения.
2
3
Bmn P( ) - вероятность перехода частицы в состояние m в единицу времени.
Bmn
Bnm – коэффициент Эйнштейна для индуцированного поглощения.
Bmn Bnm
1
2
2
a mn
e 2 3 mn rmn r * mn Amn
3
t
3h c

9.

Квантовые переходы
Многофотонные квантовые переходы
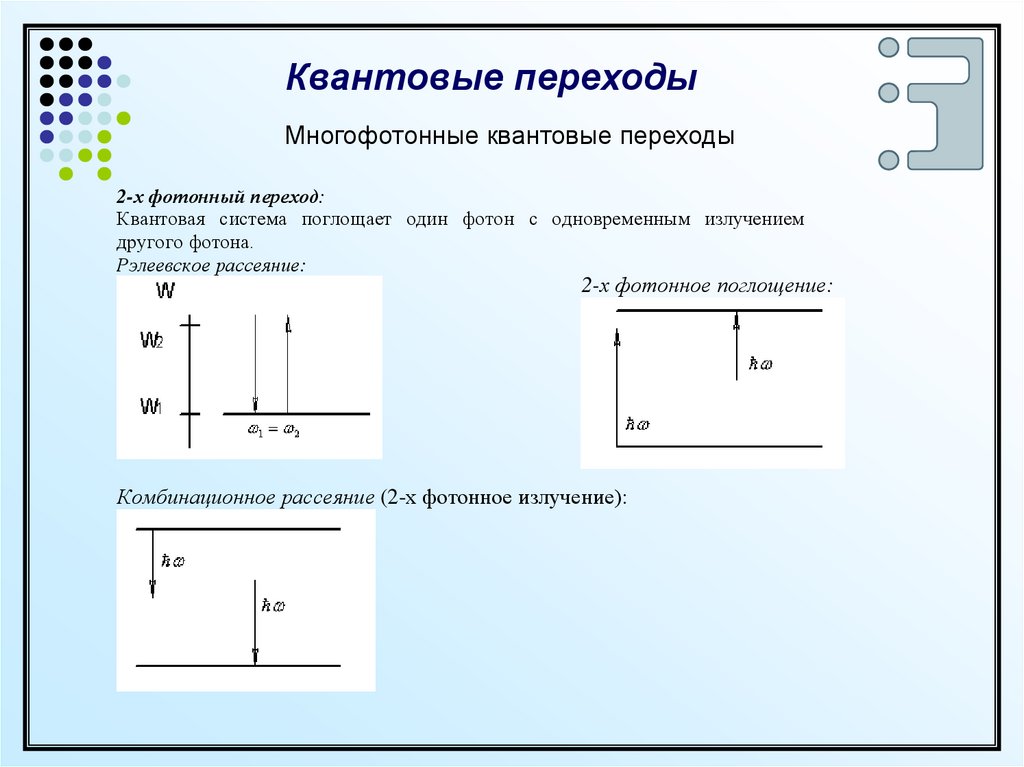
2-х фотонный переход:
Квантовая система поглощает один фотон с одновременным излучением
другого фотона.
Рэлеевское рассеяние:
2-х фотонное поглощение:
Комбинационное рассеяние (2-х фотонное излучение):

10.

Квантовые переходы
Многофотонные квантовые переходы
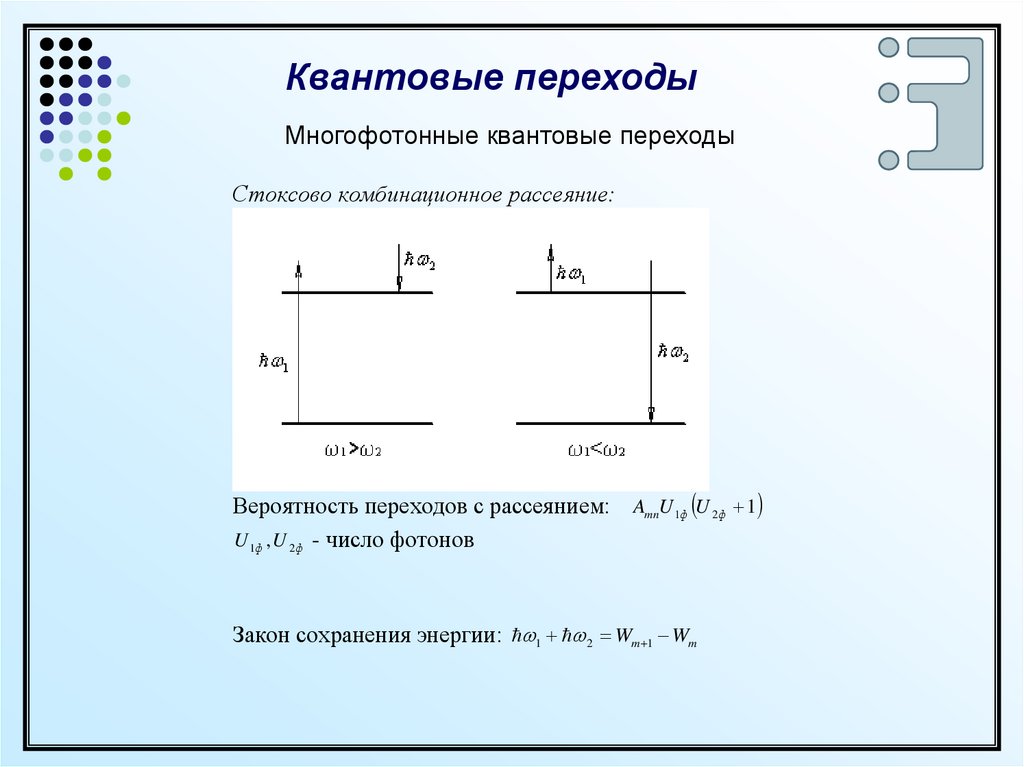
Стоксово комбинационное рассеяние:
Вероятность переходов с рассеянием: AmnU 1ф U 2ф 1
U 1ф , U 2 ф - число фотонов
Закон сохранения энергии: 1 2 Wm 1 Wm

11.

Квантовые переходы
Многофотонные квантовые переходы
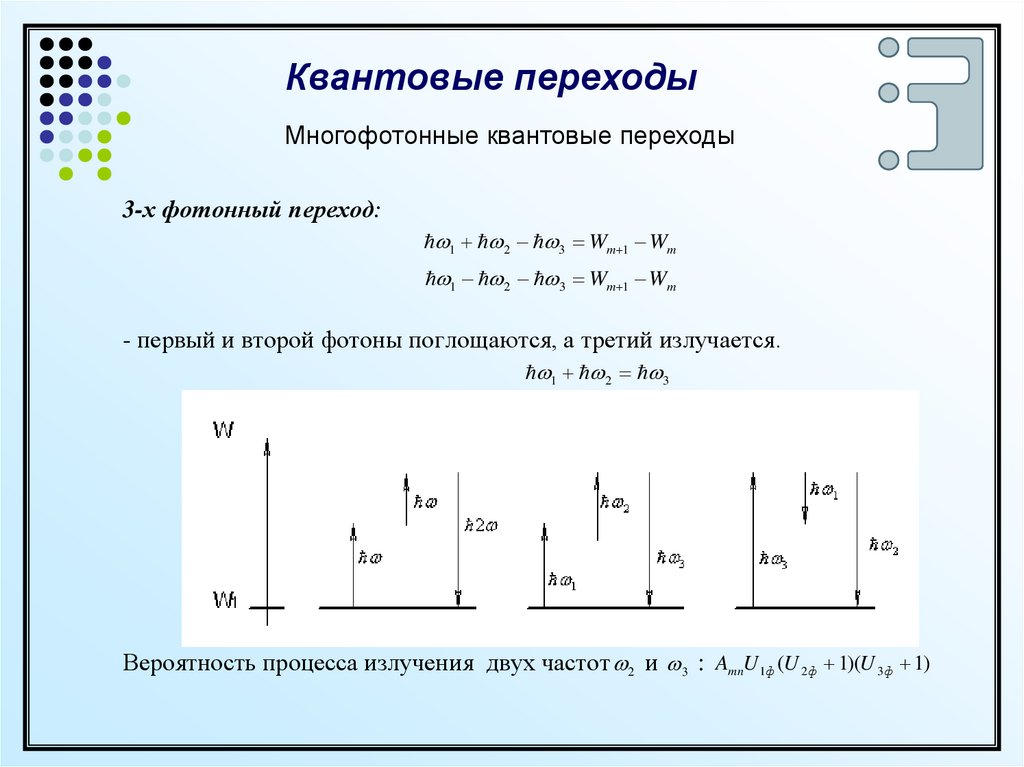
3-х фотонный переход:
1 2 3 Wm 1 Wm
1 2 3 Wm 1 Wm
- первый и второй фотоны поглощаются, а третий излучается.
1 2 3
Вероятность процесса излучения двух частот 2 и 3 : AmnU 1ф (U 2ф 1)(U 3ф 1)