Similar presentations:
Оптические свойства квантоворазмерных гетероструктур
1. Оптические свойства квантоворазмерных гетероструктур
1. Локализация носителей заряда в тонких («квантоворазмерных») узкозонных слоях- квантовых ямах.
2. Структура зон и плотность состояний в квантовых ямах.
3. Оптическое поглощение и усиление в квантовых ямах.
4. За пределами элементарной модели
5. Инжекционные лазеры с активным слоем в виде квантовых ям.
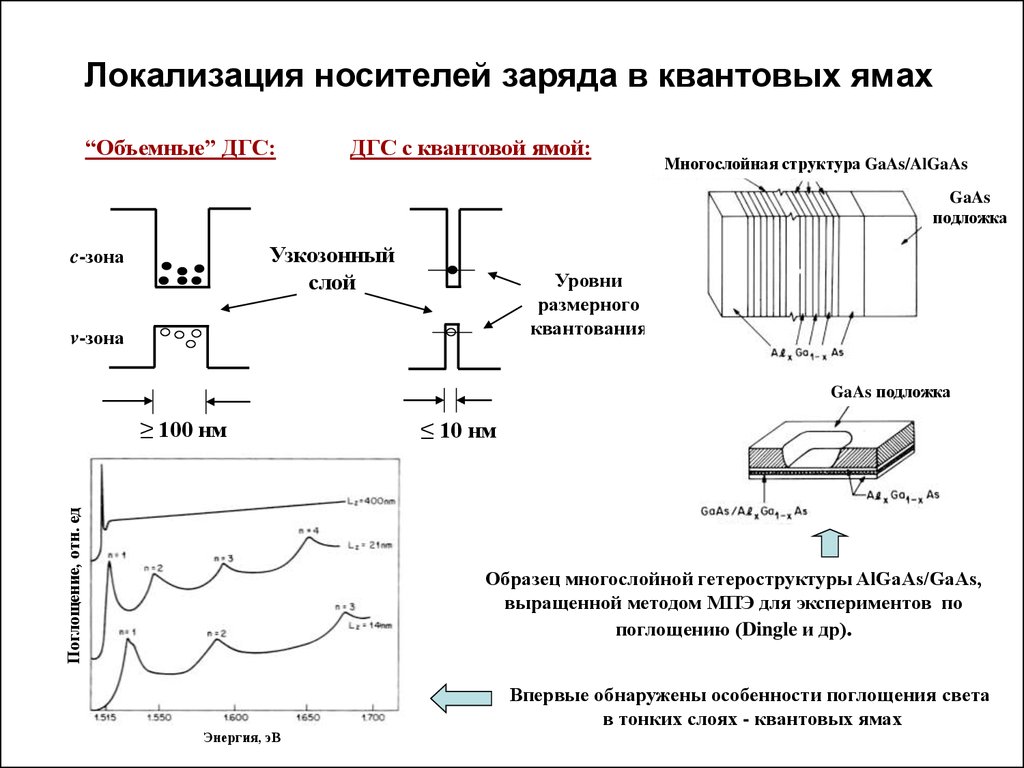
2. Локализация носителей заряда в квантовых ямах
“Объемные” ДГС:ДГС с квантовой ямой:
Многослойная структура GaAs/AlGaAs
GaAs
подложка
Узкозонный
слой
c-зона
Уровни
размерного
квантования
v-зона
GaAs подложка
Поглощение, отн. ед
≥ 100 нм
≤ 10 нм
Образец многослойной гетероструктуры AlGaAs/GaAs,
выращенной методом МПЭ для экспериментов по
поглощению (Dingle и др).
Впервые обнаружены особенности поглощения света
в тонких слоях - квантовых ямах
Энергия, эВ
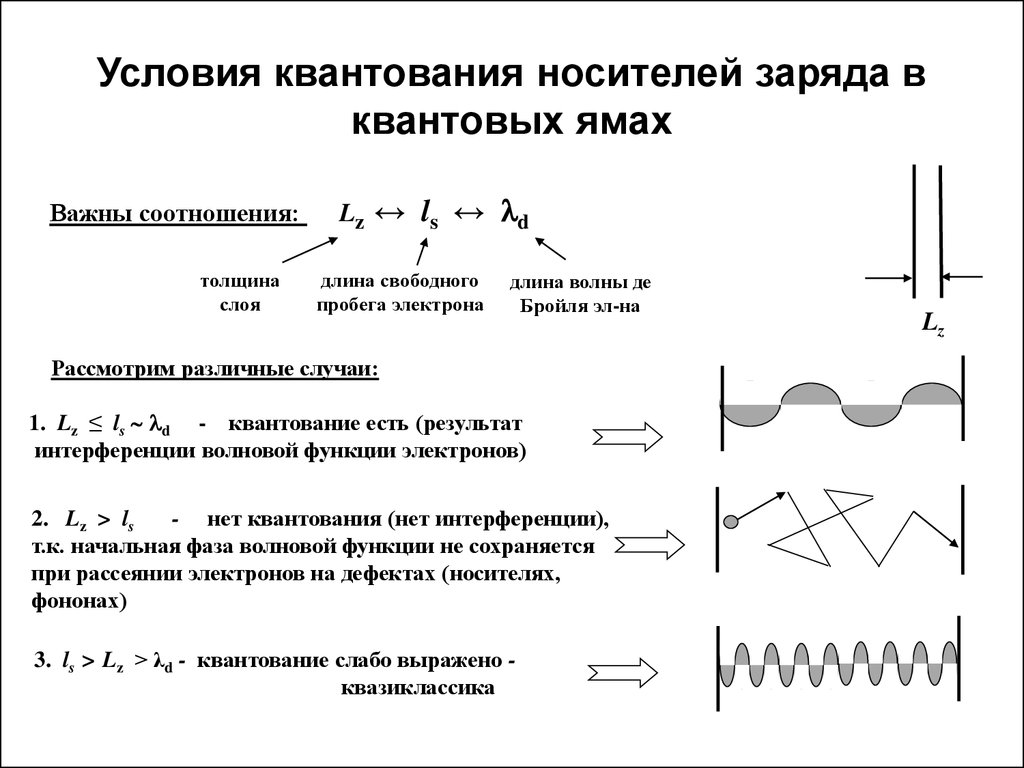
3. Условия квантования носителей заряда в квантовых ямах
Важны соотношения:толщина
слоя
Lz
↔ ls ↔ l d
длина свободного
пробега электрона
длина волны де
Бройля эл-на
Рассмотрим различные случаи:
1. Lz ≤ ls ld - квантование есть (результат
интерференции волновой функции электронов)
2. Lz > ls
- нет квантования (нет интерференции),
т.к. начальная фаза волновой функции не сохраняется
при рассеянии электронов на дефектах (носителях,
фононах)
3. ls > Lz > λd - квантование слабо выражено квазиклассика
Lz
4. Оценка параметров
Оценка ls:Оценка λd:
ld 2
ls ≈ v t . t k = 107 (см/с) . 10-13 (с) = 10-6 см = 10 нм
2k 2
2m *
k
2 m0e 2
2
2 m * m0e 2
2
ld
2 m *
2
a0e 2 m0
2 a0
2 m *
2
a0
= 0,53Ǻ - Боровский радиус;
m0e 2
Ry m0
m*
e2
Ry = 13,6 эВ – Ридберг; kT; m0/m* 10
2 a0
Подставим числа:
ld 2 a0
0
Ry m0
13.6 ( эВ)
6
,
3
0
.
53
10 10 нм
2
kT m
2.510 (эВ)
При Lz ≤ 10 нм есть квантование
(при этих параметрах квазиклассика не реализуется)
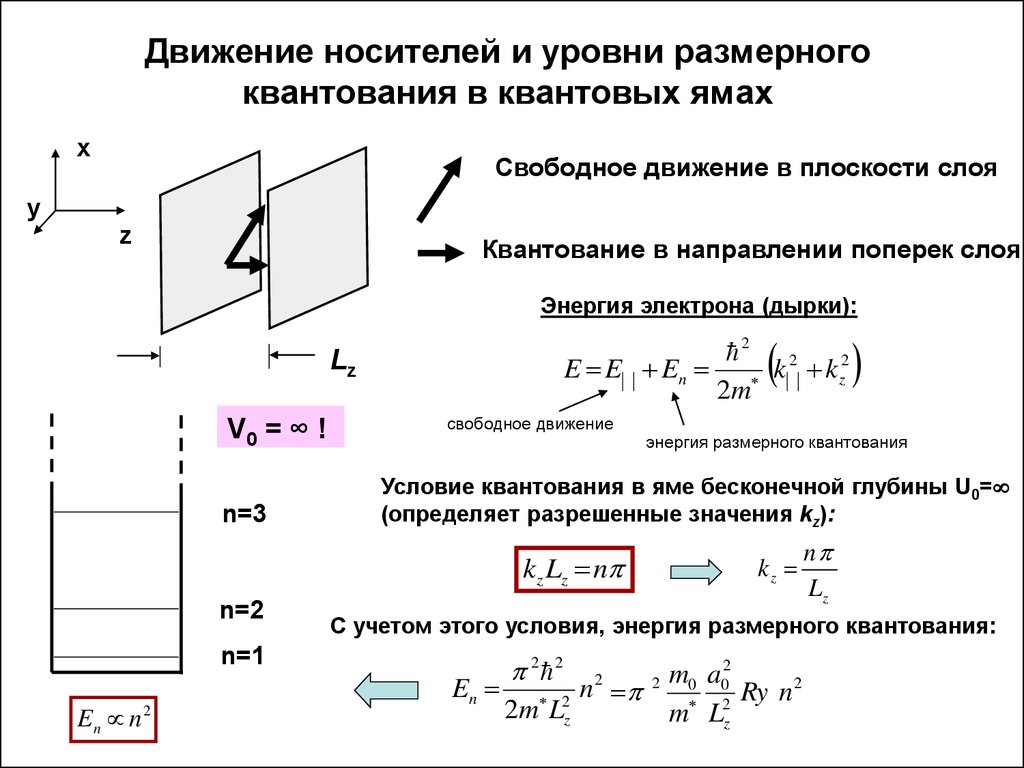
5. Движение носителей и уровни размерного квантования в квантовых ямах
xСвободное движение в плоскости слоя
y
z
Квантование в направлении поперек слоя
Энергия электрона (дырки):
2 2
E E En
k k z2
2m
Lz
V0 = ∞ !
n=3
свободное движение
энергия размерного квантования
Условие квантования в яме бесконечной глубины U0=
(определяет разрешенные значения kz):
k z Lz n
n=2
n=1
En n 2
kz
n
Lz
С учетом этого условия, энергия размерного квантования:
2 2
m0 a02
2
En 2 n
Ry
n
2m Lz
m L2z
2
2
6. Волновые функции локализованных состояний
В яме бесконечно большой глубины U0= изрешения уравнения Шредингера находим :
n=3
n=2
n ( c ,v )
n
sin
V
Lz
z exp ik r
u c,v r
- в яме
0 - вне ямы
n=1
Вид волновых функций
различных уровней
Обычно считают, что вид функций uc,v такой же, как и в
объемном материале. Это оправдано, если на размере ямы
содержится хотя бы несколько периодов решетки кристалла
7. Уровни размерного квантования в структурах AlGaAs/GaAs (конечная глубина ямы)
Пример: GaAs/Al0.3Gao.7As, Lz(GaAs) = 10 нмДля этой системы:
Оценка положения уровней при U0= :
DEc/DE=0,67
DEv/DE=0,33
m
En 3.8 meV 0 n 2
m
e2
Уровень
DEc=250
мэВ
e1
e2
hh1
hh2
lh1
hh3
e1
hh1
m*e = 0.06 m0
m*hh= 0.45 m0
m*lh= 0.087 m0
Энергия, мэВ
58
232 (уровень близко к краю ямы !)
8.5
34
43.5
76.5
hh2
DEv=125 мэВ
lh1
hh3
Расчет с V0= справедлив до тех пор пока положение
уровня размерного квантования не оказывается слишком
близко к реальному краю ямы (т.е. при en,hn < DEc,v)
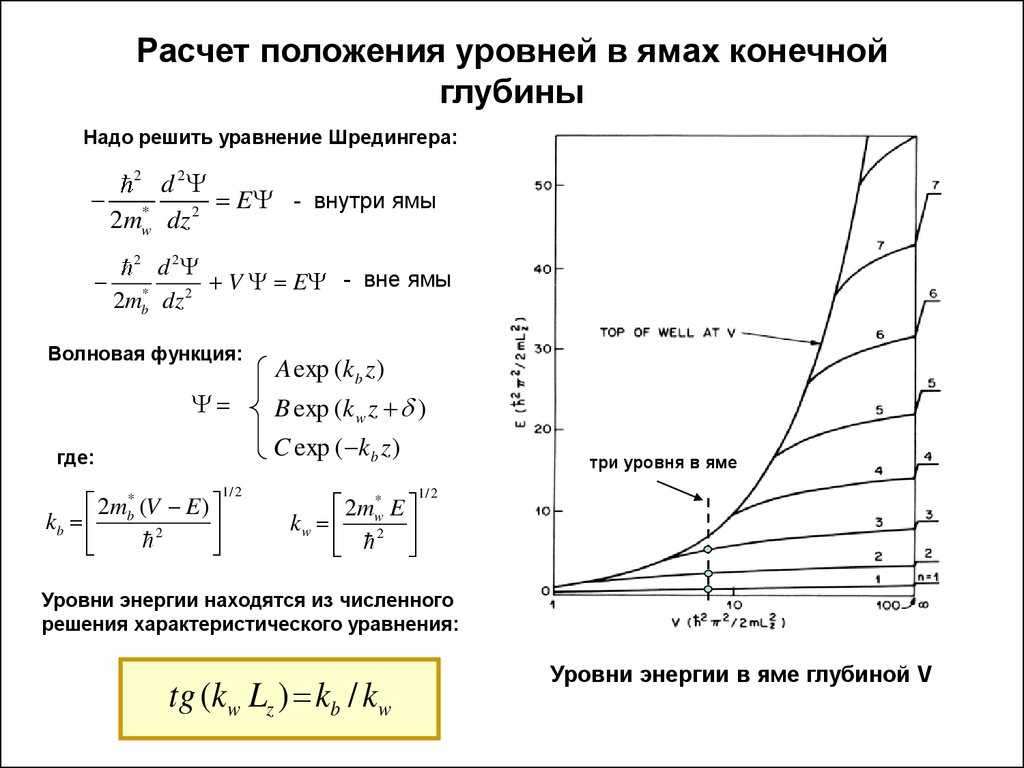
8. Расчет положения уровней в ямах конечной глубины
Надо решить уравнение Шредингера:d 2
*
E - внутри ямы
2
2mw dz
2
d 2
*
V E - вне ямы
2
2mb dz
2
Волновая функция:
A exp (kb z )
B exp (k w z )
C exp ( kb z )
где:
2mb* (V E )
kb
2
1/ 2
2mw* E
kw 2
три уровня в яме
1/ 2
Уровни энергии находятся из численного
решения характеристического уравнения:
tg (kw Lz ) kb / kw
Уровни энергии в яме глубиной V
9. Оптические переходы между подзонами размерного квантования
c• В яме с V0= оптические переходы разрешены только
между уровнями с одинаковым “n”, например
e1→hh1, e1→lh1, e2→hh2,
(иначе волновые функции не перекрываются).
Подзона
e1
Рассматриваем только «вертикальные» переходы
(с сохранением k|| )
ħw = E÷E+dE
Сосчитаем количество пар состояний с одинаковым kװ
разделенных по энергии на E÷E+dE:
Eg
kװ
1) Условие квантования в плоскости:
v
k x L 2 m ; k y L 2 m
Подзона
hh1
d kװ
2) Размер одной ячейки в плоскости в k- пространстве
k x k y
3) Количество состояний к кольцевом слое
размером k ÷װkװ+d kװ
2
2 k d k
2 2
S
2
2
S
kװ
L - размер образца по плоск.
S - площадь образца
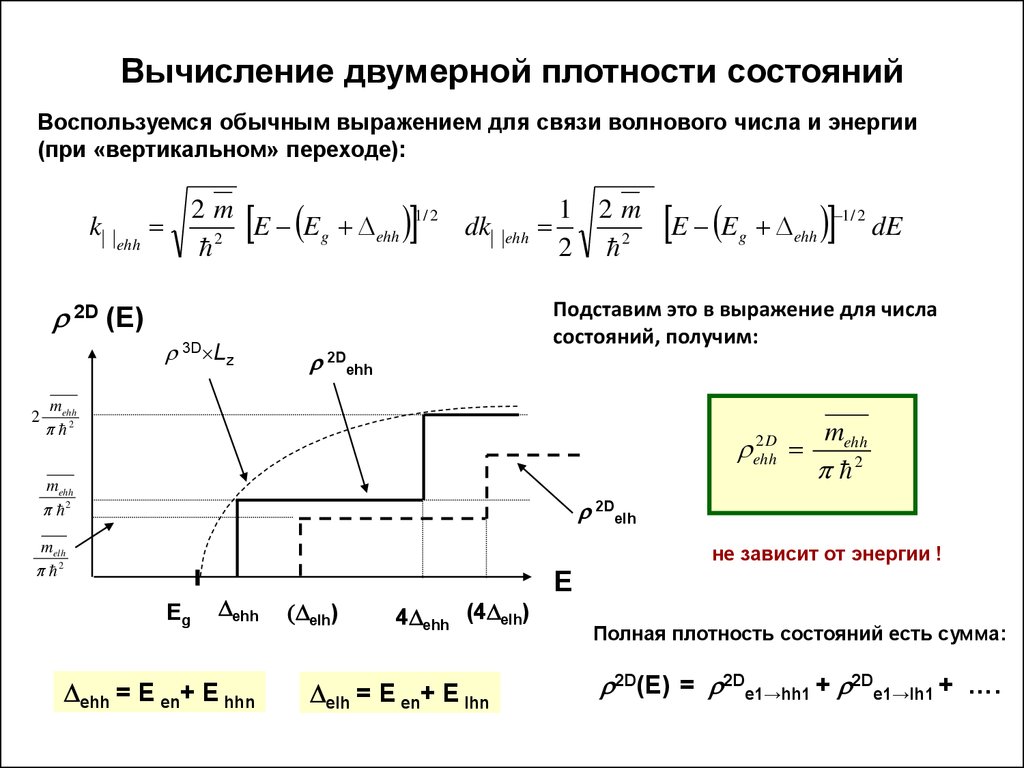
10. Вычисление двумерной плотности состояний
Воспользуемся обычным выражением для связи волнового числа и энергии(при «вертикальном» переходе):
k
ehh
2m
1/ 2
E
E
D
dk
g
ehh
2
ehh
2D (E)
3D Lz
2
1 2m
2 2
E E
g
D ehh
1 / 2
dE
Подставим это в выражение для числа
состояний, получим:
2Dehh
mehh
2
2D
ehh
mehh
2
mehh
2
2Delh
melh
2
не зависит от энергии !
Eg
Dehh
Dehh = E en+ E hhn
Delh)
E
4Dehh (4Delh)
Delh = E en+ E lhn
Полная плотность состояний есть сумма:
2D(E) = 2De1→hh1 + 2De1→lh1 + ….
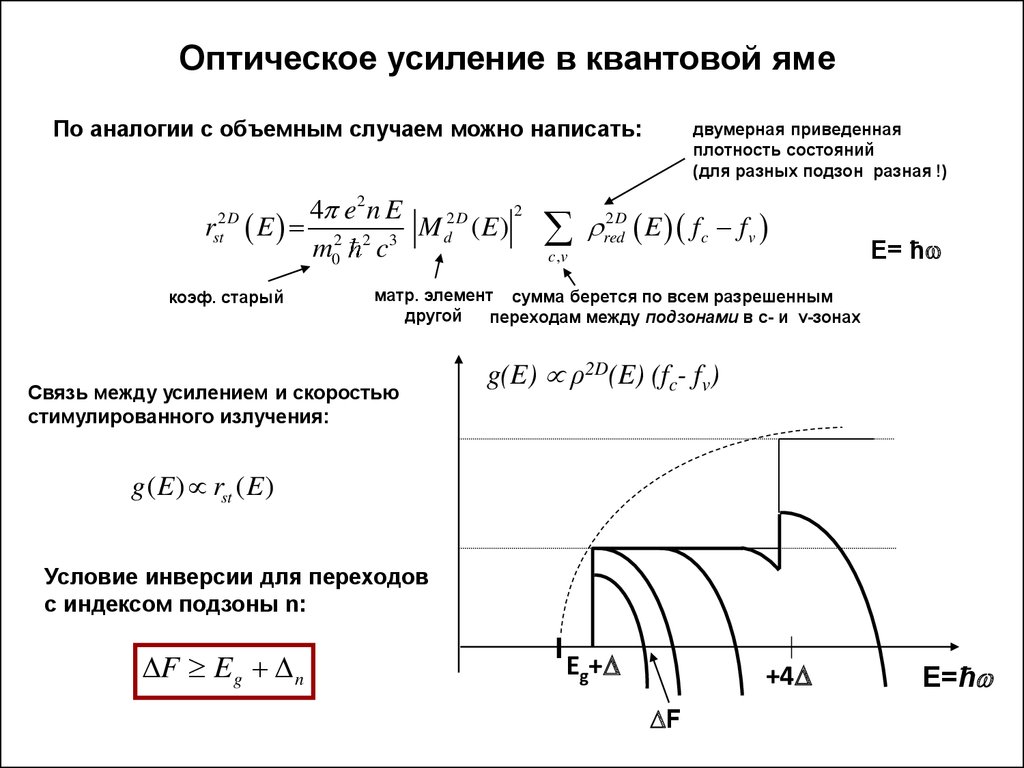
11. Оптическое усиление в квантовой яме
По аналогии с объемным случаем можно написать:2D
st
r
2
4 e2 n E
2D
E 2 2 3 M d (E)
m0 c
коэф. старый
двумерная приведенная
плотность состояний
(для разных подзон разная !)
2D
red
E fc fv
c ,v
E= ħw
матр. элемент сумма берется по всем разрешенным
другой
переходам между подзонами в с- и v-зонах
Связь между усилением и скоростью
стимулированного излучения:
g(E) ρ2D(E) (fc- fv)
g ( E ) rst ( E )
Условие инверсии для переходов
с индексом подзоны n:
DF Eg D n
Eg+D
+4D
DF
E=ħw
12. За пределами элементарной модели: Смешивание зон и дисперсия в подзонах
I. Оказывается, что в КЯ имеет место эффект смешивания зон,что приводит к изменению положения уровней
и сильной трансформации законов дисперсии:
Смешивание зон происходит из-за взаимодействия
волновых функций электронов и дырок на стенках
ямы (в объемном случае этот эффект не играет роли)
Отрицательная эф. масса !
Для перехода e1-lh1, в точке где me*= -mlh*
Расчет дисперсии дырок в валентной зоне
с учетом смешивания зон и конечной
глубины ямы в GaAs
2D
m
1 me mlh
2
!!!
2
me mlh
13. Эффект уширения уровней
II. Как и для объемного случая, в КЯ имеет место уширение уровнейэлектронов и дырок в результате столкновений между собой и с другими
частицами.
Расчет величин уширения уровней за счет разных механизмов взаимодействия носителей
в c-подзонах:
в v-подзонах:
e-e ~1 мэВ
e-h 5-10 мэВ
e-LO 3 мэВ
h-h 20 мэВ
h-e 5-10 мэВ
h-LO 7 мэВ
1
2Γ
Уширение линий оптических переходов
описывается функцией Лоренца:
2
( w E )
( w E ) 2 2
ħω
Усиление в КЯ есть свертка предыдущего выражения для g(ћω) c функцией Лоренца
g ( w) A dE
M
n n ,
n ,n
2
2 D E Eg Dn,n , f c f v w E
=[ h, l ]
E
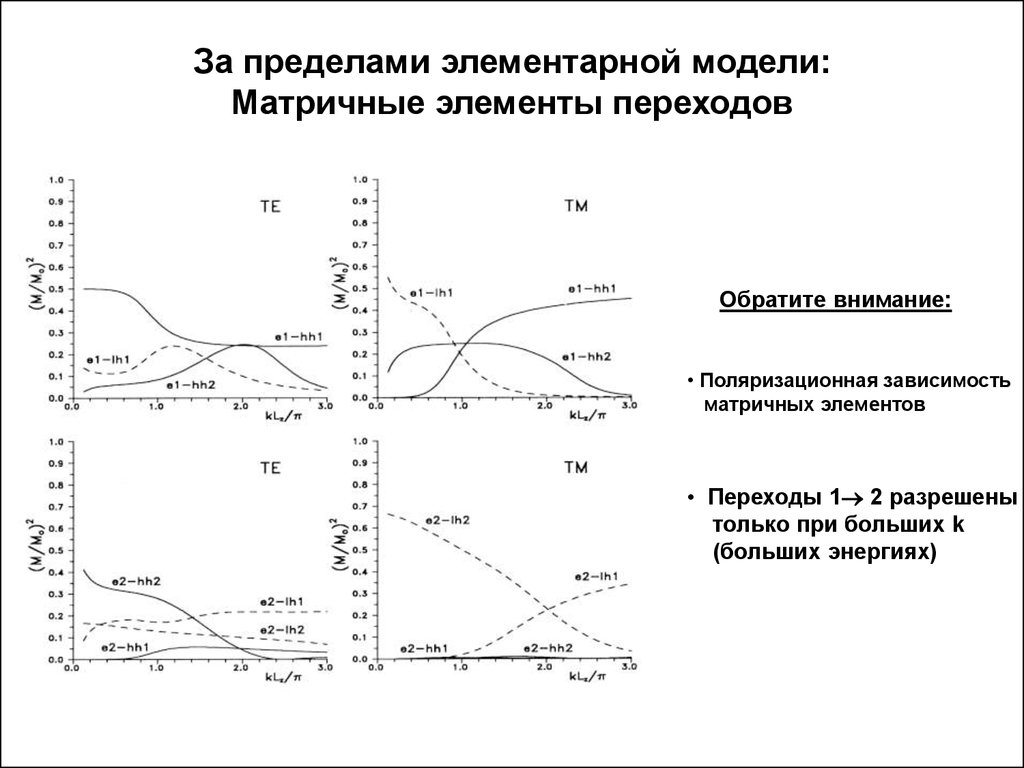
14. За пределами элементарной модели: Матричные элементы переходов
Обратите внимание:• Поляризационная зависимость
матричных элементов
• Переходы 1 2 разрешены
только при больших k
(больших энергиях)
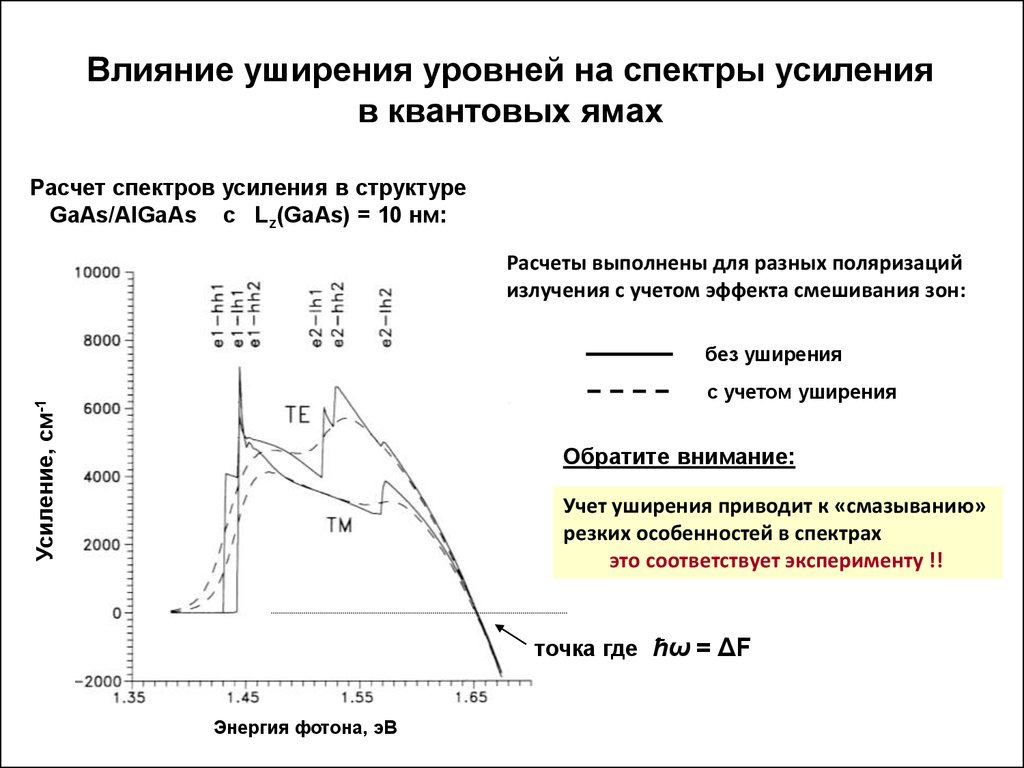
15. Влияние уширения уровней на спектры усиления в квантовых ямах
Расчет спектров усиления в структуреGaAs/AlGaAs с Lz(GaAs) = 10 нм:
Расчеты выполнены для разных поляризаций
излучения с учетом эффекта смешивания зон:
без уширения
Усиление, см-1
с учетом уширения
Обратите внимание:
Учет уширения приводит к «смазыванию»
резких особенностей в спектрах
это соответствует эксперименту !!
точка где ħω = ΔF
Энергия фотона, эВ
16. Метод измерения коэффициента усиления
Структура лазера (MBE, Lz=10 нм):Imax
Imi
n
Ширина канала ≈ 1 мкм!
1 1
g l i ln ln
L R
r l 1
r l 1
r (l )
I max (l )
I min (l )
i – внутренние потери в рез-ре, L – длина рез-ра, R- коэфф. отражения
B.W. Hakki and T.I. Pauli, J Appl. Phys. (1975) 46, 1299
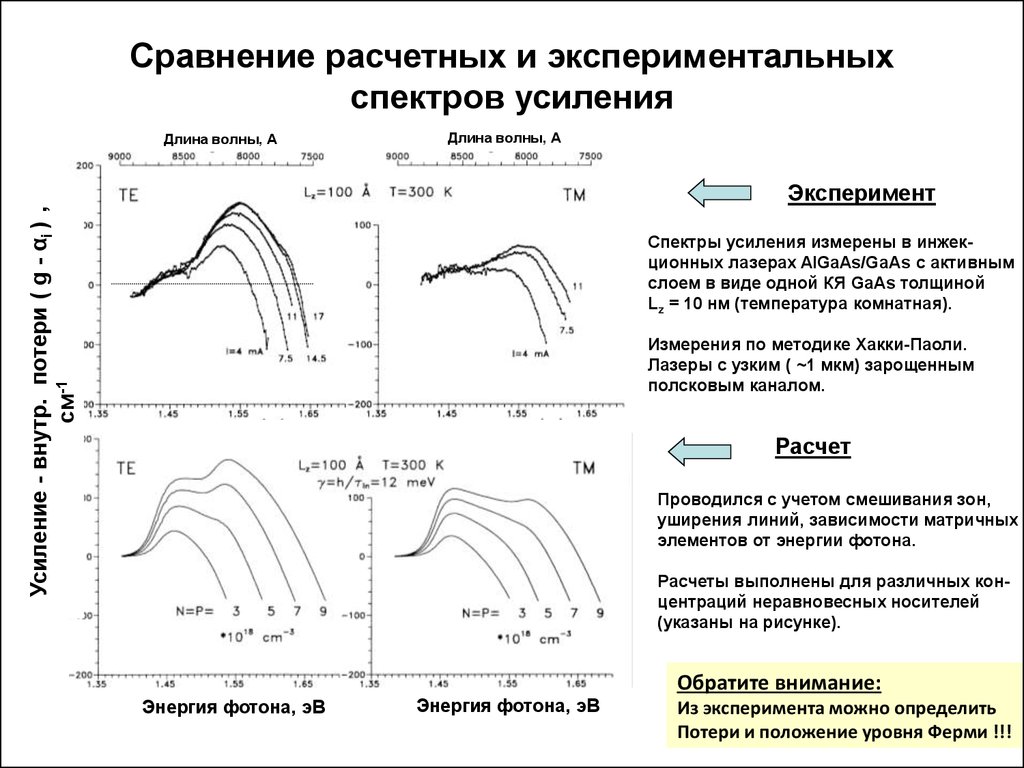
17. Сравнение расчетных и экспериментальных спектров усиления
Длина волны, АДлина волны, А
Усиление - внутр. потери ( g - αi ) ,
см-1
Эксперимент
Спектры усиления измерены в инжекционных лазерах AlGaAs/GaAs c активным
слоем в виде одной КЯ GaAs толщиной
Lz = 10 нм (температура комнатная).
Измерения по методике Хакки-Паоли.
Лазеры с узким ( ~1 мкм) зарощенным
полсковым каналом.
Расчет
Проводился с учетом смешивания зон,
уширения линий, зависимости матричных
элементов от энергии фотона.
Расчеты выполнены для различных концентраций неравновесных носителей
(указаны на рисунке).
Обратите внимание:
Энергия фотона, эВ
Энергия фотона, эВ
Из эксперимента можно определить
Потери и положение уровня Ферми !!!








 physics
physics








