Основные определения кинематики. Равноускоренное прямолинейное движение

1. 1. Основные определения кинематики 2. Равноускоренное прямолинейное движение 3. Движение тела в поле силы тяжести 4.

следующая страница
СОДЕРЖАНИЕ
1. Основные определения кинематики
2. Равноускоренное прямолинейное движение
3. Движение тела в поле силы тяжести
4. Равномерное движение по окружности
5. Законы Ньютона
6. Силы в механике - I
7. Особенности использования II закона Ньютона при решении задач
повышенной сложности
8. Силы в механике – II
9. Элементы статики
10. Гидростатика
11. Импульс и закон его сохранения
12. Работа и мощность. Механическая энергия и её сохранение
13. Закон сохранения энергии
14. Основные понятия молекулярно-кинетической теории (МКТ)

2.

предыдущая страница
следующая страница
15. Задачи по газовой теории повышенной сложности
16. Переходы вещества из одного агрегатного состояния в другое
17. Внутренняя энергия, теплота и работа в термодинамике
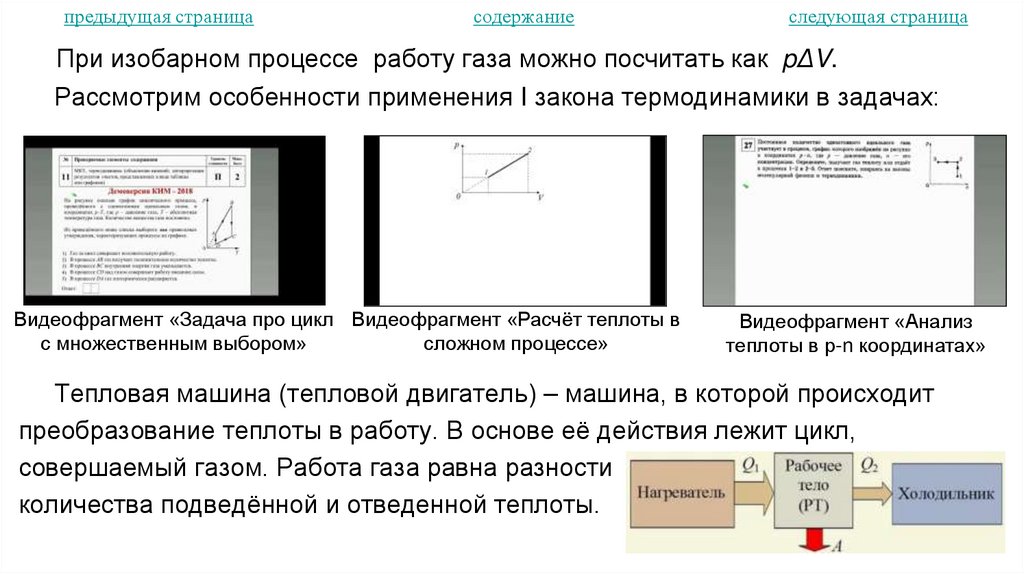
18. Первый закон термодинамики. Тепловые машины
19. Электрические заряды. Закон Кулона.
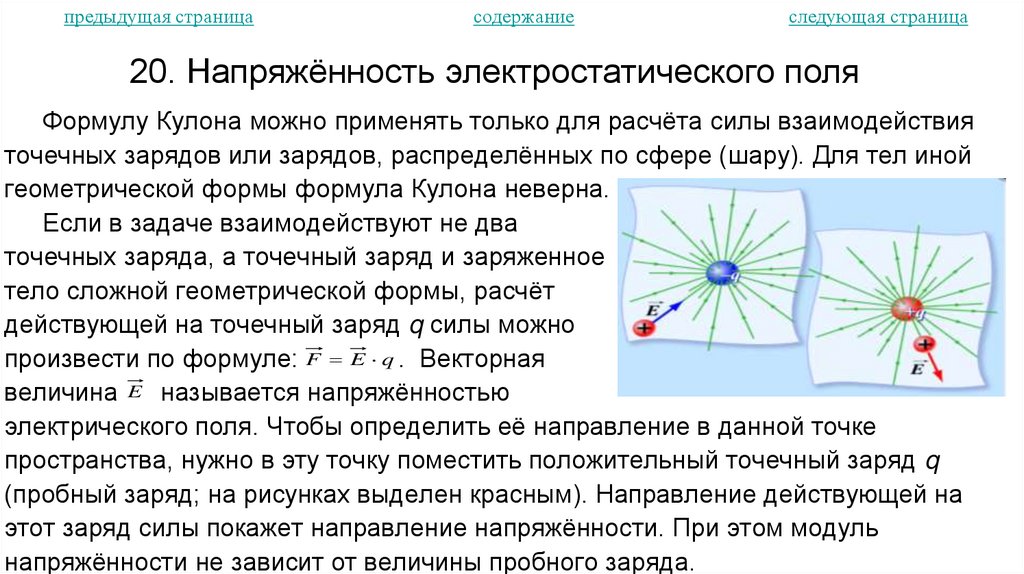
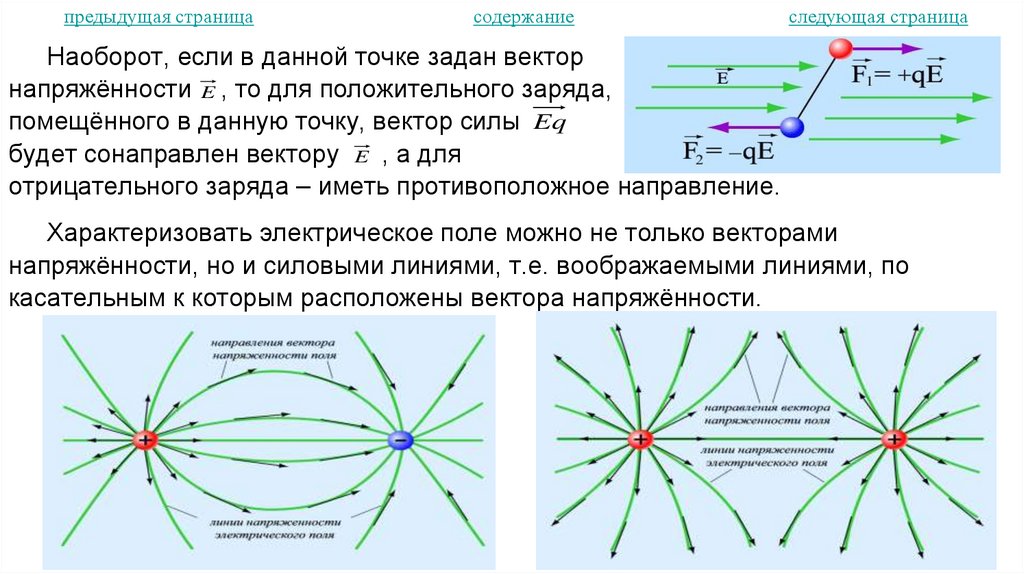
20. Напряжённость электростатического поля
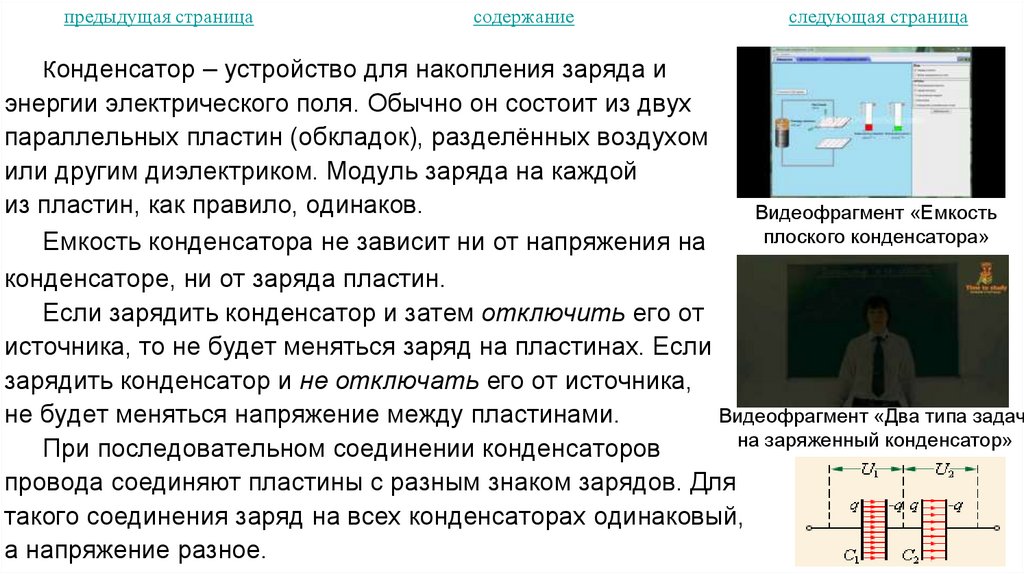
21. Потенциал и работа электростатического поля. Конденсатор
22. Проводники и диэлектрики в электростатическом поле
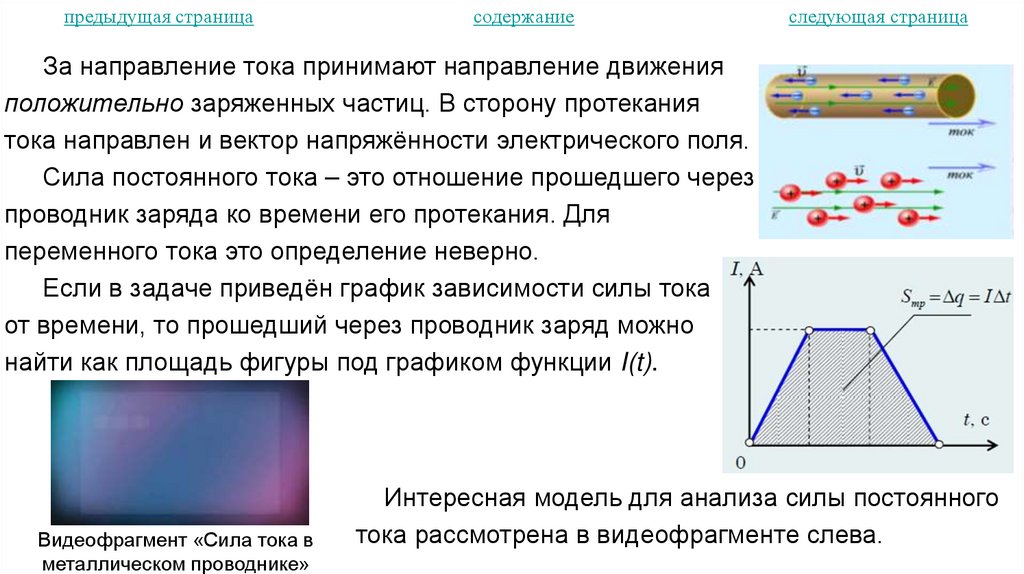
23. Электрический ток
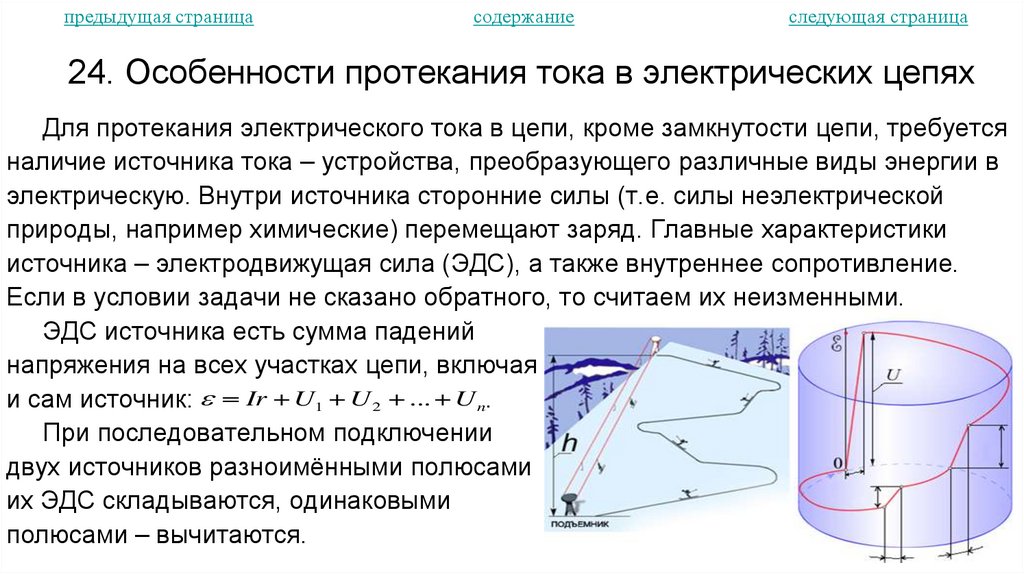
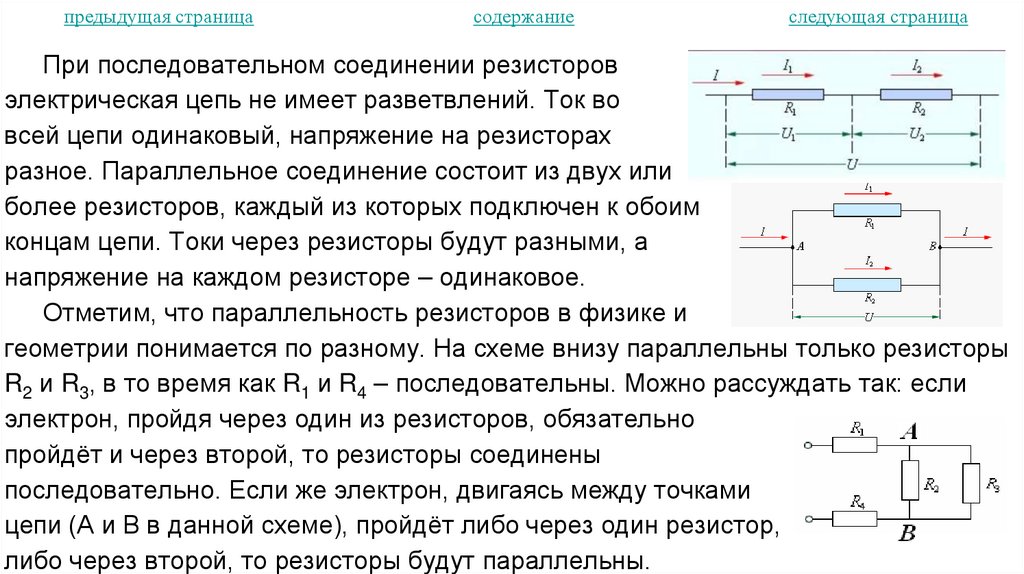
24. Особенности протекания тока в электрических цепях
25. Работа и мощность тока
26. Конденсаторы в электрических цепях
27. Нелинейные процессы в электрических цепях
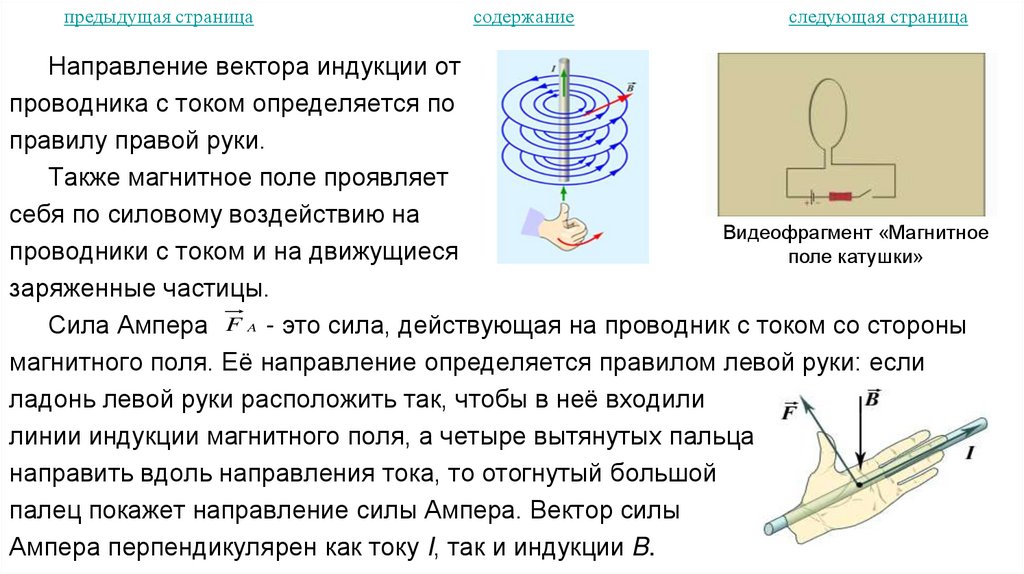
28. Магнитное поле
29. Особенности расчётных задач по магнитному полю
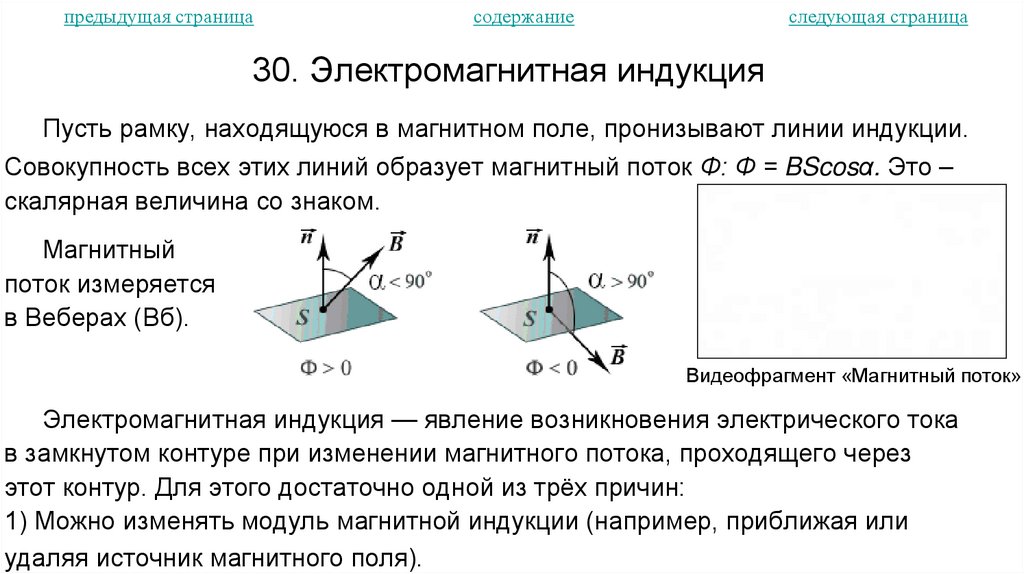
30. Электромагнитная индукция

3.

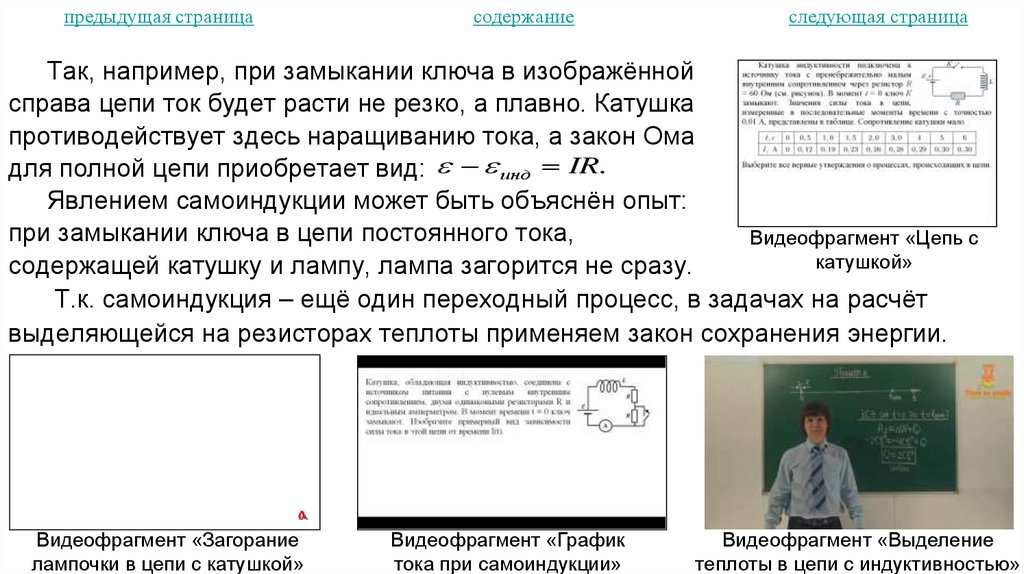
предыдущая страница
31. Катушка в электрических цепях. Трансформатор
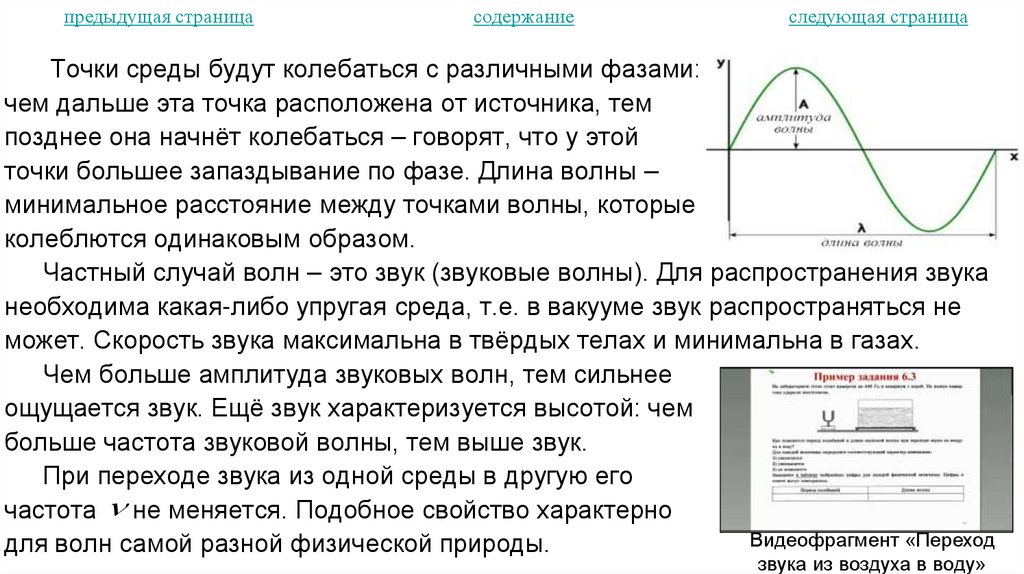
32. Механические колебания и волны
33. Электромагнитные колебания
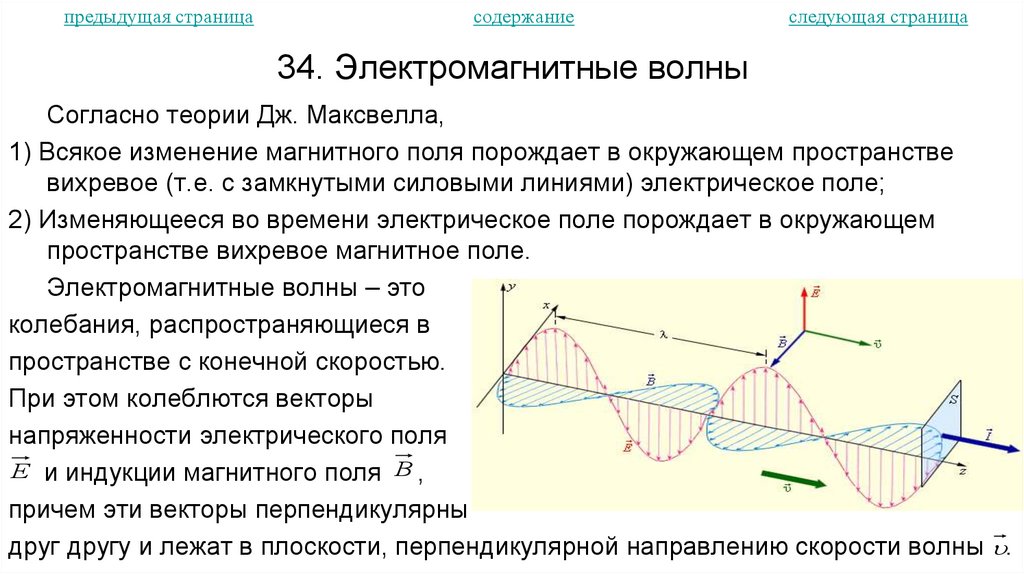
34. Электромагнитные волны
35. Геометрическая оптика
36. Волновая оптика
37. Корпускулярно-волновой дуализм
38. Строение атомов
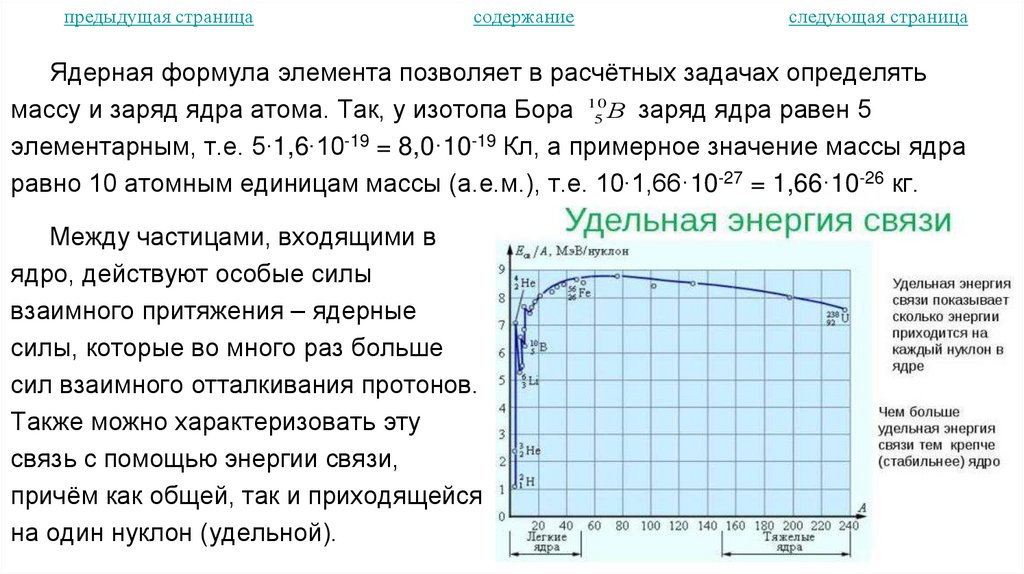
39. Радиоактивность. Ядерные реакции
40. Эксперименты в физике
следующая страница

4. 1. Основные определения кинематики

предыдущая страница
содержание
следующая страница
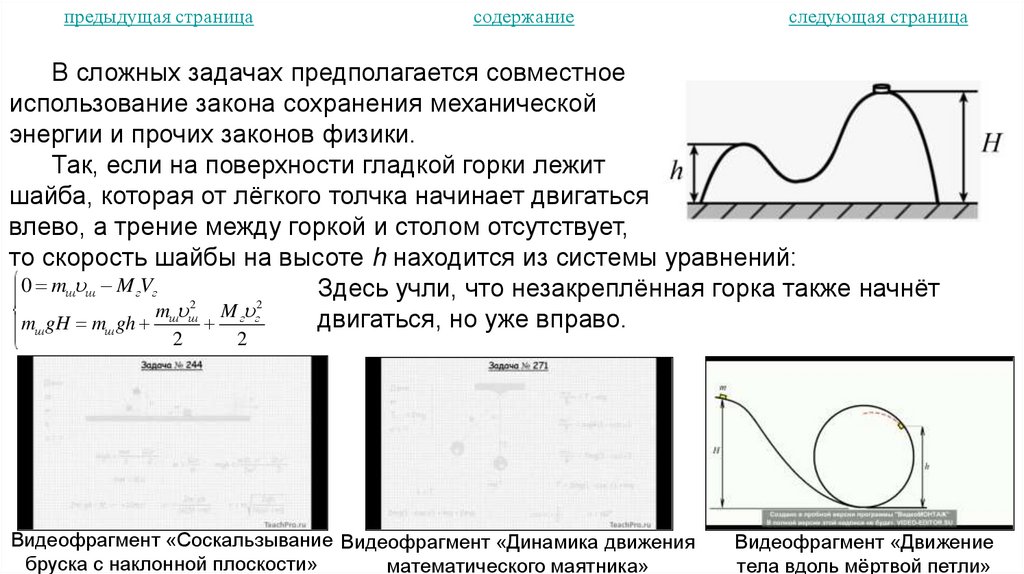
1. Основные определения кинематики
В физике ряд величин являются векторными. Векторы характеризуют длиной
(модулем), направлением и точкой приложения. Основные операции с векторами –
сложение, вычитание, проецирование.
При нахождении суммы векторов следует помнить, что модуль суммы не
обязательно равен сумме модулей. Это же справедливо и для разности векторов.
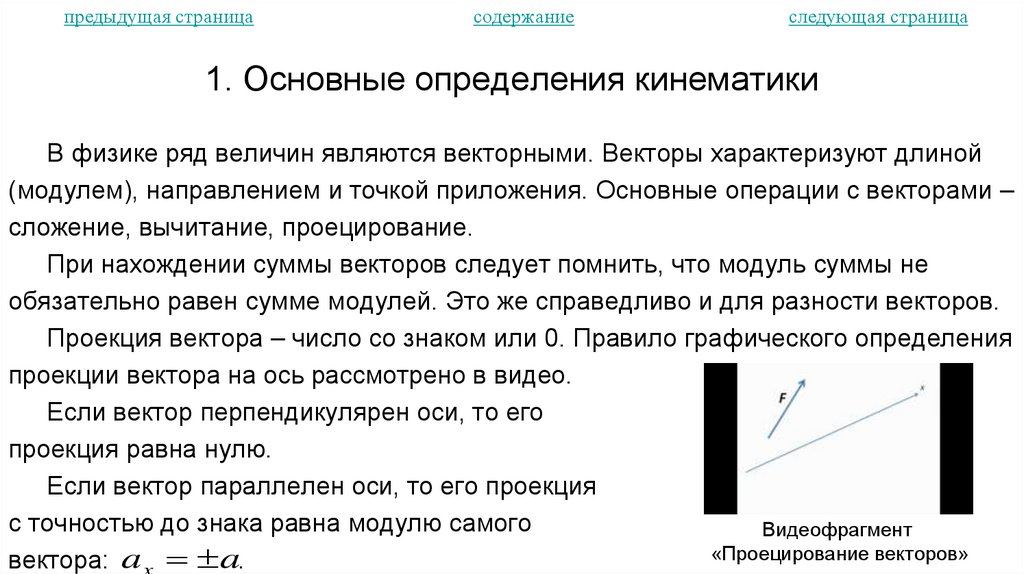
Проекция вектора – число со знаком или 0. Правило графического определения
проекции вектора на ось рассмотрено в видео.
Если вектор перпендикулярен оси, то его
проекция равна нулю.
Если вектор параллелен оси, то его проекция
с точностью до знака равна модулю самого
Видеофрагмент
«Проецирование векторов»
вектора: a x a.

5. Видеофрагмент «Зависимость формы траектории от системы отсчёта»

предыдущая страница
содержание
следующая страница
Кинематика – раздел физики, изучающий законы движения.
Материальная точка – тело, размерами которого в условиях данной задачи
можно пренебречь. Также материальной точкой можно считать тело, движущееся
поступательно. При таком движении все точки тела
описывают по форме одну и ту же траекторию.
Траектория материальной точки — линия в
пространстве, состоящая из точек, в которых
находилась материальная точка при своём движении
относительно выбранной системы отсчёта.
Видеофрагмент «Зависимость формы
траектории от системы отсчёта»
Движение в школьной физике рассматривается
в системе отсчёта, которая обычно включает начало отсчёта, одну или две
координатные оси и время. На графиках, описывающих такое движение, время
откладывается вдоль оси абсцисс.

6.

предыдущая страница
содержание
следующая страница
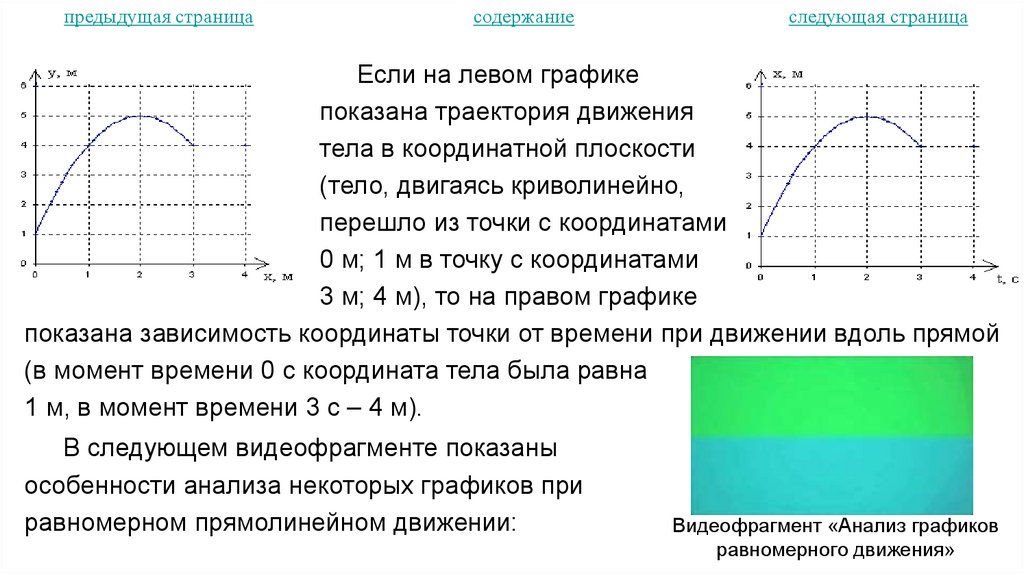
Если на левом графике
показана траектория движения
тела в координатной плоскости
(тело, двигаясь криволинейно,
перешло из точки с координатами
0 м; 1 м в точку с координатами
3 м; 4 м), то на правом графике
показана зависимость координаты точки от времени при движении вдоль прямой
(в момент времени 0 с координата тела была равна
1 м, в момент времени 3 с – 4 м).
В следующем видеофрагменте показаны
особенности анализа некоторых графиков при
равномерном прямолинейном движении:
Видеофрагмент «Анализ графиков
равномерного движения»

7.

предыдущая страница
содержание
следующая страница
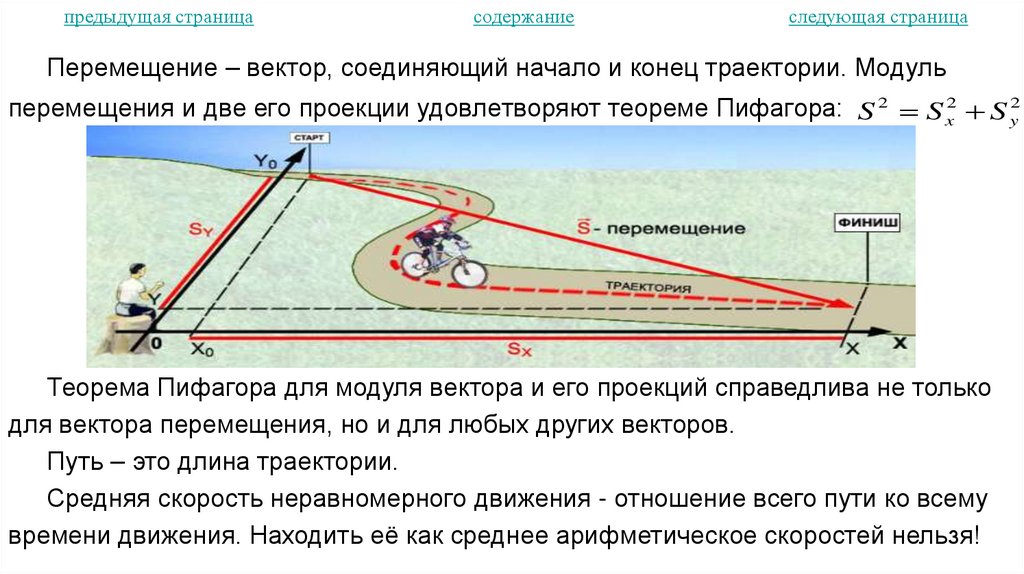
Перемещение – вектор, соединяющий начало и конец траектории. Модуль
перемещения и две его проекции удовлетворяют теореме Пифагора: S 2 S x2 S y2
Теорема Пифагора для модуля вектора и его проекций справедлива не только
для вектора перемещения, но и для любых других векторов.
Путь – это длина траектории.
Средняя скорость неравномерного движения - отношение всего пути ко всему
времени движения. Находить её как среднее арифметическое скоростей нельзя!

8. Видеофрагмент «Относительность скорости автомобилей»

предыдущая страница
содержание
следующая страница
Скорость движения в кинематике – величина относительная, т.е. она зависит
от того, в какой системе отсчёта мы её рассматриваем. Так, если первое тело
движется относительно фиксированной системы отсчёта (например, земли) со
скоростью 1 , второе – со скоростью 2, то скорость первого тела в системе
отсчёта, связанной со вторым телом, рассчитывается как 1 2 , т.е. по правилу
нахождения разности векторов. Если тела не движутся вдоль одной прямой, то
решение таких задач связано с анализом треугольников, составленных из этих
векторов (как правило, прямоугольных).
Видеофрагмент «Относительность
скорости автомобилей»
Видеофрагмент «Переправа
лодки через реку»

9. 2. Равноускоренное прямолинейное движение

предыдущая страница
содержание
следующая страница
2. Равноускоренное прямолинейное движение
Говорят, что тело движется вдоль прямой равноускоренно,
если за любые одинаковые промежутки времени своего
движения скорость тела изменяется на одну и ту же величину
а 0. Векторная величина а называется ускорением.
Функциональная зависимость
координаты х от времени t
2
at
здесь имеет вид х х0 0t
. Таким образом, коэффициент,
2
стоящий перед t, является проекцией начальной скорости, а
коэффициент, стоящий перед t2 – половиной проекции
ускорения.
Также можно определить скорость как производную функции координаты по
времени, а ускорение – как производную скорости, или как вторую производную
координаты. Данный подход возможен для описания произвольного, а не только
равноускоренного движения.

10.

предыдущая страница
содержание
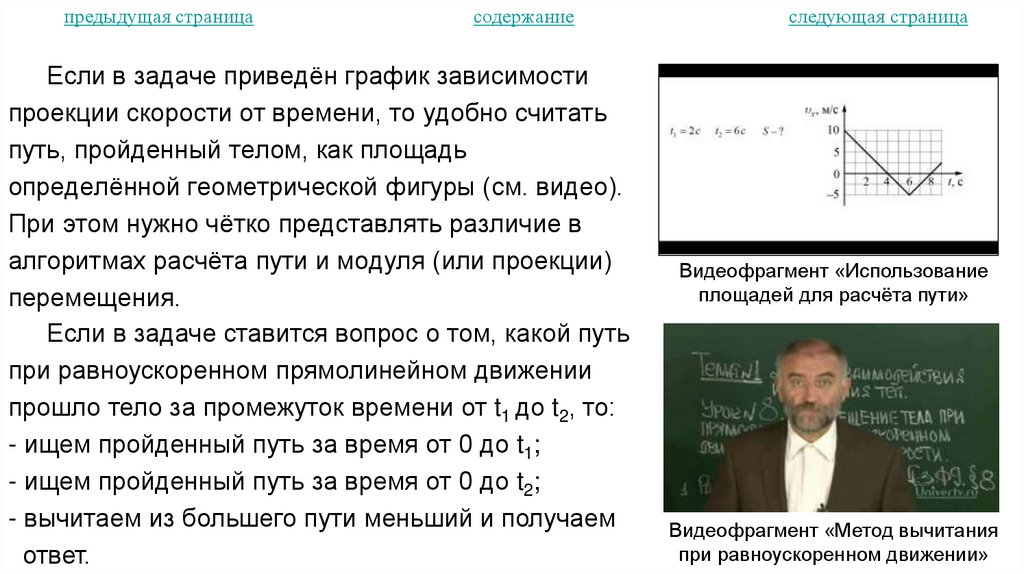
Если в задаче приведён график зависимости
проекции скорости от времени, то удобно считать
путь, пройденный телом, как площадь
определённой геометрической фигуры (см. видео).
При этом нужно чётко представлять различие в
алгоритмах расчёта пути и модуля (или проекции)
перемещения.
Если в задаче ставится вопрос о том, какой путь
при равноускоренном прямолинейном движении
прошло тело за промежуток времени от t1 до t2, то:
- ищем пройденный путь за время от 0 до t1;
- ищем пройденный путь за время от 0 до t2;
- вычитаем из большего пути меньший и получаем
ответ.
следующая страница
Видеофрагмент «Использование
площадей для расчёта пути»
Видеофрагмент «Метод вычитания
при равноускоренном движении»

11.

предыдущая страница
содержание
следующая страница
Аналогично («методом вычитания») можно решать и задачу о том, сколько
времени потребуется телу для прохождения пути между точками 1 и 2 траектории:
t = t2 – t1, где t2 – время движения тела от начала движения до точки 2, t1 – время
движения тела от начала движения до точки 1.
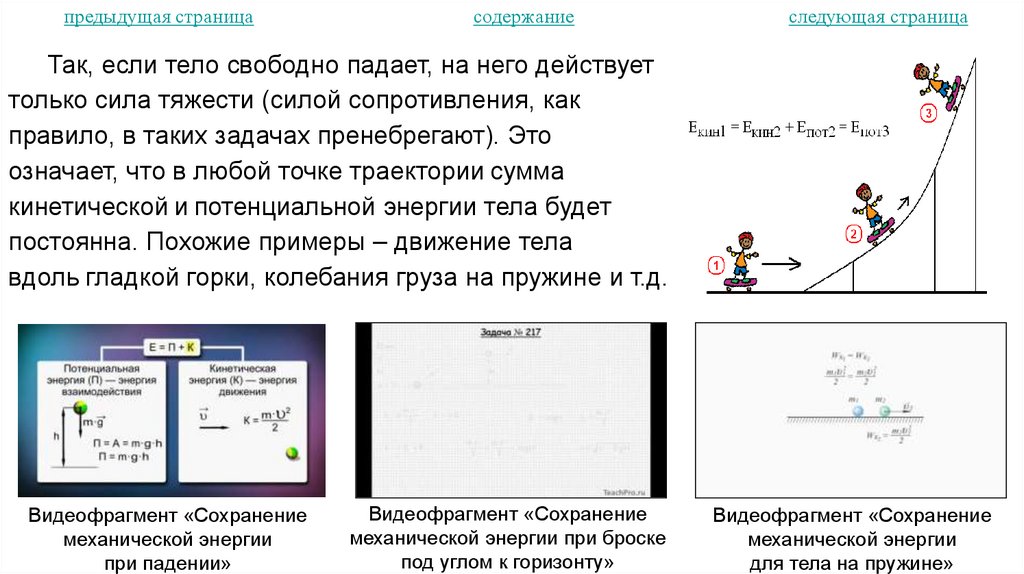
Частный случай равноускоренного движения – свободное падение. Тело,
брошенное снизу вверх или падающее сверху вниз, при отсутствии сопротивления
со стороны воздуха движется с ускорением свободного падения g 10 м/с2 .(знак
проекции ускорения зависит от выбора направления координатной оси).
Видеофрагмент «Координата, скорость
и ускорение при вертикальном броске»
Видеофрагмент «Метод вычитания в
задаче на свободное падение»

12. 3. Движение тела в поле силы тяжести

предыдущая страница
содержание
следующая страница
3. Движение тела в поле силы тяжести
Если тело движется около поверхности Земли, а
вектор его начальной скорости не нулевой и не
вертикальный, то тело будет двигаться по сложной
траектории (дуге параболы). При этом ускорение тела
равно g и направлено вертикально вниз. Движение
вдоль оси ОХ будет равномерным, вдоль оси
ОУ – равноускоренным.
В видеофрагменте справа показаны принципы,
позволяющие в задачах уровня «С» выводить сложные
формулы данного раздела.
При броске тела под углом к горизонту минимальная
по модулю скорость достигается в верхней точке
траектории, при этом min х, максимальная скорость
достигается в начале и конце движения и равна max . 0
Видеофрагмент «Зависимость
проекций вектора
скорости от времени»
Видеофрагмент «Расчёт
дальности полёта тела»

13.

предыдущая страница
содержание
следующая страница
Свои особенности есть и у движения тела,
брошенного с высоты горизонтально. Так, время
полёта такого тела не зависит от начальной скорости.
Тем самым, оно такое же, как при свободном падении.
Поскольку векторы скорости тела и двух её
составляющих образуют прямоугольный
Видеофрагмент «Свободное падение
и горизонтальный бросок»
треугольник, то модуль скорости в любой момент
времени находится по теореме Пифагора. А тангенс угла между вектором скорости
и горизонтом есть отношение двух проекций вектора скорости.
Видеофрагмент «Расчёт модуля
скорости через составляющие»
Видеофрагмент «Угол
между составляющими»

14. 4. Равномерное движение по окружности

предыдущая страница
содержание
следующая страница
4. Равномерное движение по окружности
При равномерном движении по окружности за любые
одинаковые промежутки времени материальная точка
поворачивается на один и тот же угол относительно оси
вращения. Угловая скорость (читается «омега») показывает
угол этого поворота за единицу времени. В СИ измеряется в
радианах за секунду (рад/с).
Видеофрагмент
«Угловая скорость»
Частота (читается «ню») показывает, сколько оборотов совершает
материальная точка за единицу времени. В СИ измеряется в об/с или с-1
(в последующих разделах физики будет использоваться ещё одна единица
измерения частоты – герцы, Гц).
Период Т показывает, сколько времени требуется материальной точке, чтобы
совершить один полный оборот. В СИ измеряется в секундах.

15.

предыдущая страница
содержание
Вектор линейной скорости направлен по
касательной к окружности.
Т.к. при движении по окружности вектор линейной
скорости непрерывно меняется по направлению, при
таком движении есть ускорение, называемое
центростремительным. Оно направлено к центру
окружности.
Важно! Если тело неравномерно движется по
окружности, то у него есть 2 вида ускорения. Кроме
центростремительного, которое отвечает за
изменение направления движения, появляется
и касательное (или тангенциальное) ускорение,
направленное по касательной к траектории и
отвечающее за изменение модуля скорости.
следующая страница
Видеофрагмент «Расчёт
центростремительного ускорения»
Видеофрагмент
«Тангенциальное ускорение»

16. 5. Законы Ньютона

предыдущая страница
содержание
следующая страница
5. Законы Ньютона
Законы Ньютона — три закона, лежащие в основе классической механики и
позволяющие описать движение для любого тела или системы тел.
известны силы, действующие на тело или систему тел.
I закон: Существуют такие системы отсчёта (инерциальные),
относительно которых материальная точка, при отсутствии
внешних воздействий, покоится или движется равномерно и
прямолинейно. Такое свойство тела называют инерцией.
В школьных задачах инерциальные системы отсчёта (ИСО) связана с Землёй
либо с любым движущимся равномерно и прямолинейно относительно Земли
телом. Если же тело движется относительно Земли с ускорением, связанная с
таким телом система отсчёта уже не будет инерциальной.
При переходе от одной ИСО к другой обязательно сохраняется ускорение тела.

17.

предыдущая страница
содержание
следующая страница
II закон: В инерциальной системе отсчёта ускорение,
которое получает материальная точка, прямо пропорционально
равнодействующей всех приложенных к ней сил и обратно
пропорционально её массе: F ma. Равнодействующая F – это
не какая-то определённая сила, а именно что векторная сумма
всех действующих на тело сил. Масса тела – мера его инертности: чем она
больше, тем большую силу нужно приложить для изменения его скорости.
-
Из второго закона Ньютона следует, что:
если сумма всех действующих на тело сил (равнодействующая) равна 0, то
тело либо покоится, либо движется вдоль прямой с постоянной скоростью;
если равнодействующая не равна 0, то тело движется с ускорением, причём
вектор ускорения направлен туда, куда направлен вектор равнодействующей.
Вектор скорости при этом может быть направлен совершенно произвольно!

18.

предыдущая страница
содержание
следующая страница
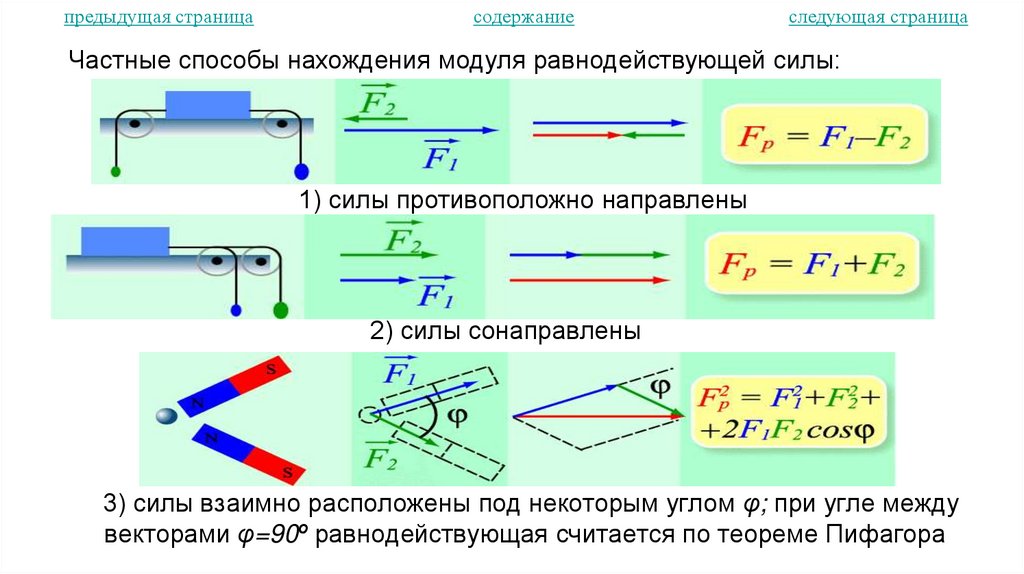
Частные способы нахождения модуля равнодействующей силы:
1) силы противоположно направлены
2) силы сонаправлены
3) силы взаимно расположены под некоторым углом φ; при угле между
векторами φ=90º равнодействующая считается по теореме Пифагора

19.

предыдущая страница
содержание
следующая страница
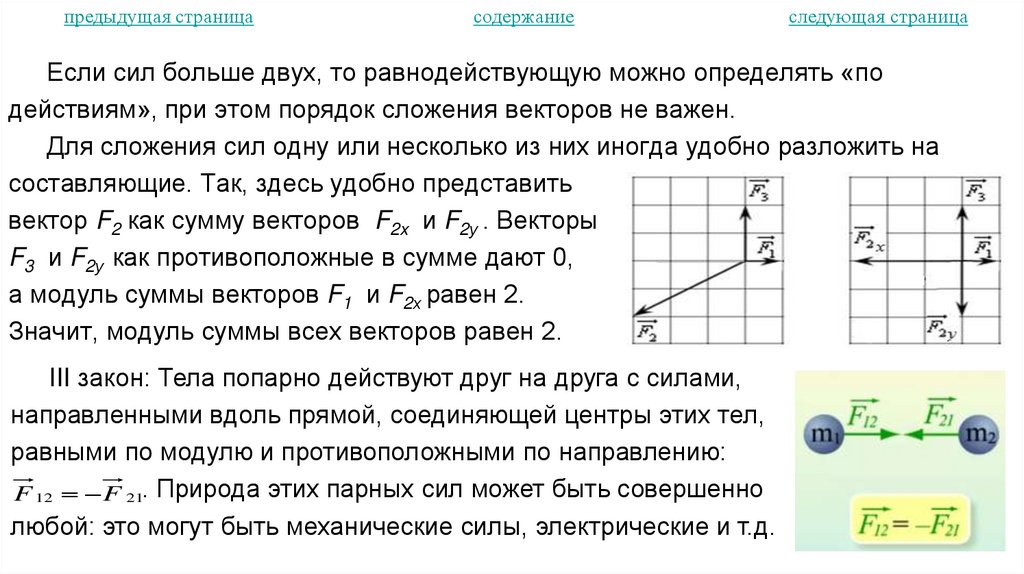
Если сил больше двух, то равнодействующую можно определять «по
действиям», при этом порядок сложения векторов не важен.
Для сложения сил одну или несколько из них иногда удобно разложить на
составляющие. Так, здесь удобно представить
вектор F2 как сумму векторов F2x и F2у . Векторы
F3 и F2у как противоположные в сумме дают 0,
а модуль суммы векторов F1 и F2х равен 2.
Значит, модуль суммы всех векторов равен 2.
III закон: Тела попарно действуют друг на друга с силами,
направленными вдоль прямой, соединяющей центры этих тел,
равными по модулю и противоположными по направлению:
F 12 F 21. Природа этих парных сил может быть совершенно
любой: это могут быть механические силы, электрические и т.д.
.

20. 6. Силы в механике - I

предыдущая страница
содержание
следующая страница
6. Силы в механике - I
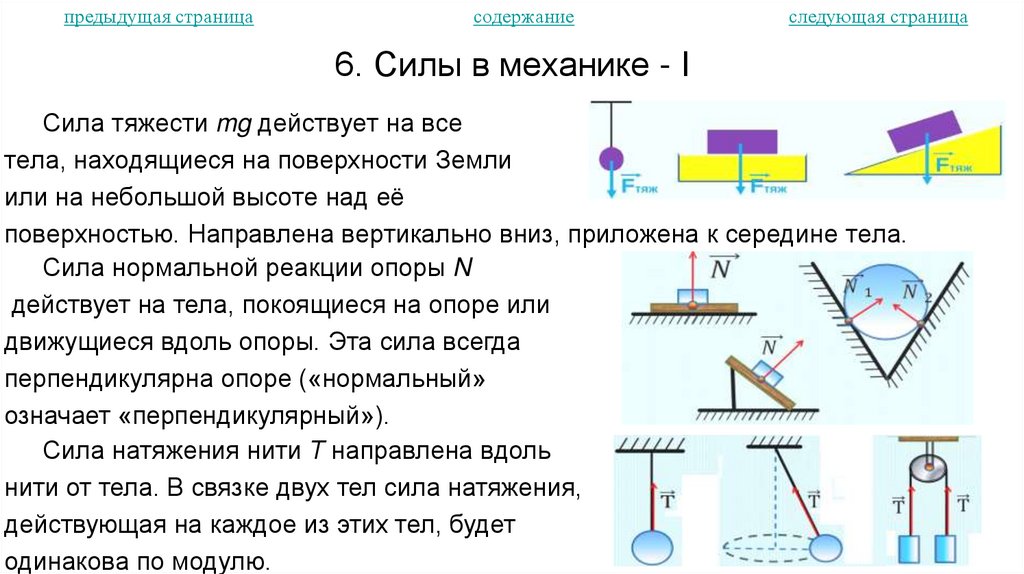
Сила тяжести mg действует на все
тела, находящиеся на поверхности Земли
или на небольшой высоте над её
поверхностью. Направлена вертикально вниз, приложена к середине тела.
Сила нормальной реакции опоры N
действует на тела, покоящиеся на опоре или
движущиеся вдоль опоры. Эта сила всегда
перпендикулярна опоре («нормальный»
означает «перпендикулярный»).
Сила натяжения нити Т направлена вдоль
нити от тела. В связке двух тел сила натяжения,
действующая на каждое из этих тел, будет
одинакова по модулю.

21.

предыдущая страница
содержание
следующая страница
Вес тела Р – это сила, которая действует
со стороны тела на опору или подвес. Для
записи второго закона Ньютона эту силу
использовать не надо, поскольку вес тела на
само тело не действует. Однако по III закону
Ньютона, модуль веса всегда равен модулю
силы реакции опоры (или силы натяжения нити): Р = N или Р = Т.
Вес тела – это совсем не то же самое,
что сила тяжести: модуль веса может быть
как больше, так и меньше модуля силы
тяжести. Если вес равен нулю (т.е. тело не
действует на опору или подвес), тело
невесомо. В частности, тело будет
невесомо, находясь в свободном полёте.

22.

предыдущая страница
содержание
Сила трения скольжения возникает при скольжении
тела вдоль трущейся поверхности. Её модуль считается по
формуле Fтр = μN. Здесь μ – безразмерный коэффициент,
принимающий значение в интервале от 0 до 1.
следующая страница
Видеофрагмент «Сила
трения скольжения»
Сила трения скольжения,
действующая на тело со стороны поверхности, и сила
трения скольжения, действующая на поверхность со
стороны тела, равны по модулю и разнонаправлены.
Внимание! Если тело покоится, то сила трения покоя
может принимать любые значения от 0 до μN. В этом
случае её расчёт по формуле Fтр = μN может привести к
ошибке; правильно же искать её из условия равенства
нулю суммы всех действующих на тело сил.
Видеофрагмент «Сила
трения покоя»

23.

предыдущая страница
содержание
следующая страница
И только если по условию задачи тело вот-вот тронется
с места, модуль силы трения покоя можно считать по
формуле Fтр. покоя макс. = μN. Как правило, в условии таких
задач нужно искать предельное значение некоторого
параметра (например, «при каком наименьшем значении Видеофрагмент «Покоящееся
тело на наклонной плоскости»
силы, приложенной к телу, оно начнёт двигаться»).
Другим примером силы, противодействующей движению, является сила
сопротивления воздуха (или какой-либо другой среды). Она направлена против
направления движения тела. В сложных расчётных задачах модуль этой силы
может быть прямо пропорционален модулю скорости или
квадрату скорости тела, т.е. Fсопр k или Fсопр k 2,
где k - некоторый постоянный коэффициент.
Сила сопротивления проявляет себя при больших
Видеофрагмент «Задача на
скоростях, при малых скоростях ею можно пренебречь.
расчёт силы сопротивления»

24. 7. Особенности использования II закона Ньютона при решении задач повышенной сложности

предыдущая страница
содержание
следующая страница
7. Особенности использования II закона Ньютона при
решении задач повышенной сложности
Ниже рассмотрим некоторые приёмы, позволяющие с помощью II закона
Ньютона решать задачи повышенной сложности.
Так, в случае связки тел обычно для каждого тела
составляют II закон Ньютона движения и решают
полученную систему уравнений.
Пример 1. По горизонтальному столу движется брусок
массой M, соединенный с грузом массой m невесомой
нерастяжимой нитью, перекинутой через гладкий невесомый
блок (см. рис.). Коэффициент трения бруска о поверхность
стола равен μ. Определите ускорение бруска.
Решение: при расстановке сил на чертеже учтём, что на
каждое из таких тел действует одинаковая по модулю сила
натяжения нити Т, ускорение а тоже по модулю одинаковое.

25.

предыдущая страница
содержание
следующая страница
Для тела М II закон в проекциях на вертикаль имеет вид: N Mg 0 N mg.
Тогда для обоих тел в проекциях на горизонталь получим:
mg Mg
a
M m
Если блок в условии задачи подвижный, то модули ускорений тел будут
отличаться (обычно в 2 раза).
Пример 2. На наклонной горке с углом при основании α
находится неподвижное тело массой m. Чему равен модуль
действующей на тело силы трения?
Решение: выберем координатную ось вверх вдоль горки и
спроецируем все векторы на эту ось. С учётом того, что
проекция N будет равна нулю (этот вектор перпендикулярен оси проецирования), и
o
ускорение равно нулю, II закон Ньютона примет вид: Fтр mg cos(90 ) 0 ,
или Fтр mg sin (а вовсе не Fтр N !)

26.

предыдущая страница
содержание
следующая страница
Формула Fтр N будет верна только для такого
угла наклона плоскости αпред. (предельного угла), когда
вот-вот начнётся соскальзывание тела вниз (пример 3,
см. видео). Запоминаем красивое соотношение: μ = tgαпред.
Пример 4. По горизонтальной поверхности под
действием силы F, направленной под углом α к горизонту,
движется брусок массой m. Коэффициент трения бруска о
поверхность стола равен μ. Определите ускорение бруска.
Видеофрагмент «Определение
коэффициента трения»
Решение: спроецируем вектора на ось движения и
получим уравнение: F cos N ma. Здесь 2 неизвестные:
а и N. При этом ни в коем случае нельзя считать, что N=mg.
Для расчёта N спроецируем все векторы на вертикальную
ось, получим: N F sin mg 0. Выразив N и подставив
в первое уравнение, получим: a
F cos ( mg F sin )
.
m

27.

предыдущая страница
содержание
следующая страница
При решении задачи о соскальзывании тела с
наклонной плоскости при заданном коэффициенте
трения (пример 6, см. справа) получается интересный
вывод: ускорение тела не зависит от его массы.
Наконец, с помощью проецирования на две оси
Видеофрагмент «Скольжение
тела по наклонной плоскости»
решается и известная задача про «лебедя, рака и
щуку», т.е. задача про 3 силы (две из которых перпендикулярны), дающие в сумме
0. Проецирование здесь приводит к системе:
.
F
Далее можно либо поделить уравнения, получив tg 2 ,
F3
либо возвести эти уравнения в квадрат и сложить, что с
учётом основного тригонометрического тождества даёт
F12 F22 F32.
.

28. 8. Силы в механике – II

предыдущая страница
содержание
следующая страница
8. Силы в механике – II
Модуль силы упругости пружины (жгута) считается по
формуле Fупр = kx. Здесь k – коэффициент жесткости,
x (или Δx, Δℓ) – деформация, т.е. модуль разности длин
пружины в обычном и напряжённом состоянии. Эта сила
действует в направлении, противоположном деформации.
Из данной формулы следует, что при линейном
увеличении нагрузки деформация тоже растёт линейно.
Однако этот закон (закон Гука) верен только для малых
деформаций; для больших деформаций связь между x
и Fупр не является линейной. Так, для приведённой на
графике зависимости между деформацией х и силой
упругости закон Гука выполняется только до значения деформации, равной 2 см.

29.

предыдущая страница
содержание
следующая страница
Сила тяготения (или гравитационная сила)
– это сила, с которой взаимно притягиваются
любые два тела. Её модуль рассчитывается по
mm
формуле FT G R1 2 2 , где m1 и m2 - массы тел;
R - расстояние между их центрами; G –
гравитационная постоянная.
Силы, с которыми взаимно притягиваются тела по закону всемирного
тяготения, направлены вдоль прямой, соединяющей центры этих тел.
Частный случай силы тяготения – сила тяжести.
Здесь одним из взаимодействующих тел является
планета.
С использованием закона всемирного тяготения
выводятся формулы для описания движения спутника,
т.е. тела, вращающегося по круговой орбите вокруг
Видеофрагмент
планеты.
«Космические скорости»

30.

предыдущая страница
содержание
следующая страница
Для вывода формулы скорости спутника II закон Ньютона для него был записан
в виде: F mа ц , где ац - центростремительное ускорение.
При переходе на более дальнюю орбиту линейная
скорость и центростремительное ускорение спутника
уменьшаются, период обращения вокруг планеты –
увеличивается.
Подобный метод можно использоваться для
Видеофрагмент «Переход
спутника на другую орбиту»
описания движения по окружности любых тел.
Пример. Тело соскальзывает с полусферы радиуса R и отрывается от неё в
точке, в которой радиус образует с вертикалью угол α.
Чему равна скорость тела при отрыве?
Решение. Учтём, что в момент отрыва N = 0. II закон
Ньютона в проекциях на ось Х радиус-вектора:
.
2
mg cos m
gR cos
R

31.

предыдущая страница
содержание
следующая страница
Важное замечание: в предыдущем примере проецировать нужно именно на
ось, проходящую через центр сферы; если взять другую ось, то уравнение сильно
усложнится. Вспомним, что при неравномерном движении по окружности тело
испытывает как центростремительное ускорение (направлено к центру
окружности), так и тангенциальное ускорение (направлено по касательной к
окружности). Чтобы обнулить проекцию тангенциального ускорения в решении,
рекомендуется проецировать векторы именно на ось радиуса.
Рассмотрим ещё несколько задач на движение по окружности:
Видеофрагмент «Невесомость
при движении по мосту»
Видеофрагмент
«Конический маятник»
Видеофрагмент «Поворот под
действием трения»

32. 9. Элементы статики

предыдущая страница
содержание
следующая страница
9. Элементы статики
Статика - раздел механики, изучающий условия равновесия тела.
Момент силы относительно точки О - это величина,
равная произведению модуля силы на плечо: M = F