Веб.1. Механика 2025

1.

МЕХАНИКА. ОБЗОР ОСНОЫХ
ПОЛОЖЕНИЙ
Автор: Ханчич Олег Алексеевич, д.х.н., профессор
Контакты: khanol@yandex.ru
Москва – 2025

2.

Механика
область физики, изучающая движение материальных
объектов и взаимодействие между ними, а также законы изменения
положений тел в пространстве со временем и причины,
вызывающие это перемещение.
Важнейшими разделами механики являются классическая
механика, релятивистская механика и квантовая механика.
Механика
Классическая
Релятивистская
механика
механика
υ«c
υ~c
Работа силы тяжести
Квантовая
механика
(движение
микрочастиц )

3. Классическая механика

Классическая механика основана на законах
Ньютона и принципе относительности
Галилея. Поэтому ее часто называют
«Ньютоновской
механикой».
Статикарассматривает равновесие тел. Кинематикаизучает геометрическое свойство движения
без рассмотрения его причин. Динамикарассматривает движение тел.

4. Кинематика материальной точки

Основные понятия кинематики:
Материальная точка – это тело, обладающее массой,
размерами которого можно пренебречь в условиях данной задачи.
Системой отсчета называется совокупность системы координат,
тела, к которому привязана эта система координат и измерителя
времени
Траекторией движения точки называется линия, описываемая
этой точкой в пространстве.

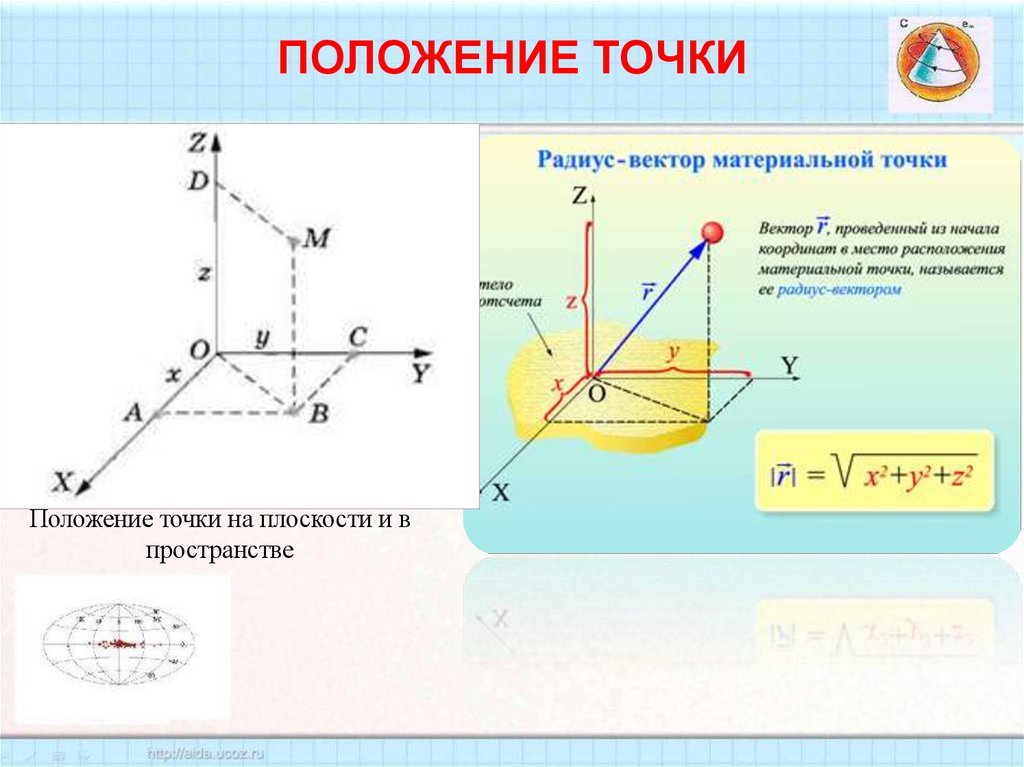
5. ПОЛОЖЕНИЕ ТОЧКИ

Положение точки на плоскости и в
пространстве

6. Cкорость и ускорение

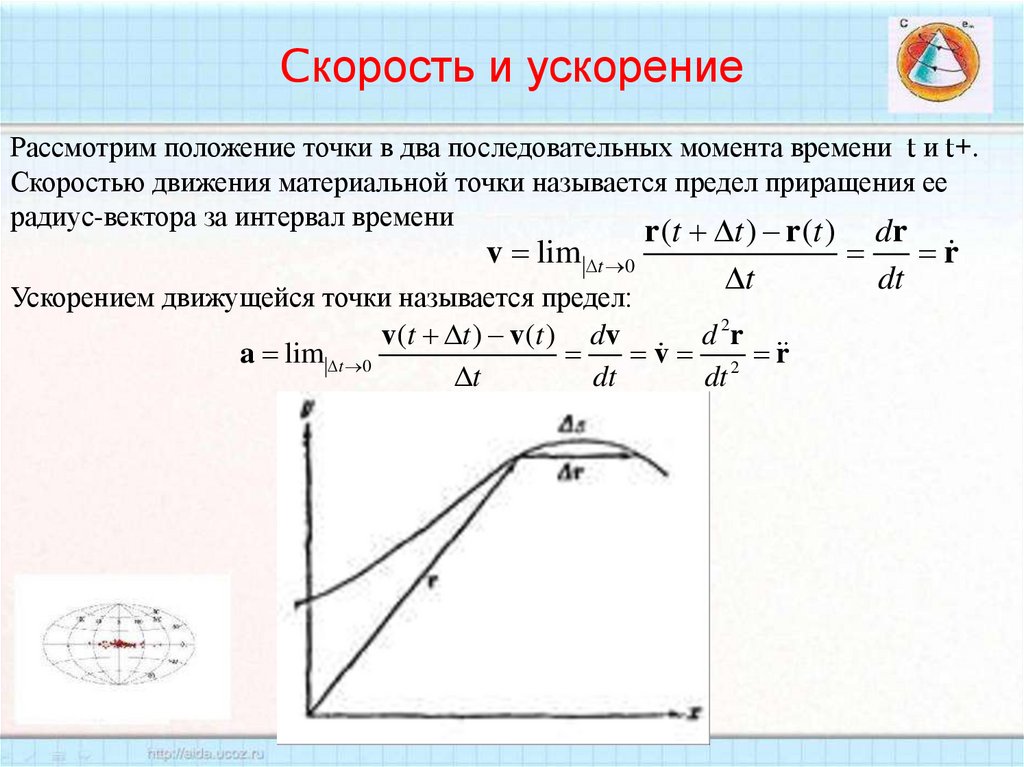
Рассмотрим положение точки в два последовательных момента времени t и t+.
Скоростью движения материальной точки называется предел приращения ее
радиус-вектора за интервал времени
r (t t ) r (t ) dr
v lim t 0
r
t
dt
Ускорением движущейся точки называется предел:
v(t t ) v(t ) dv
d 2r
a lim t 0
v 2 r
t
dt
dt

7. Движение материальной точки

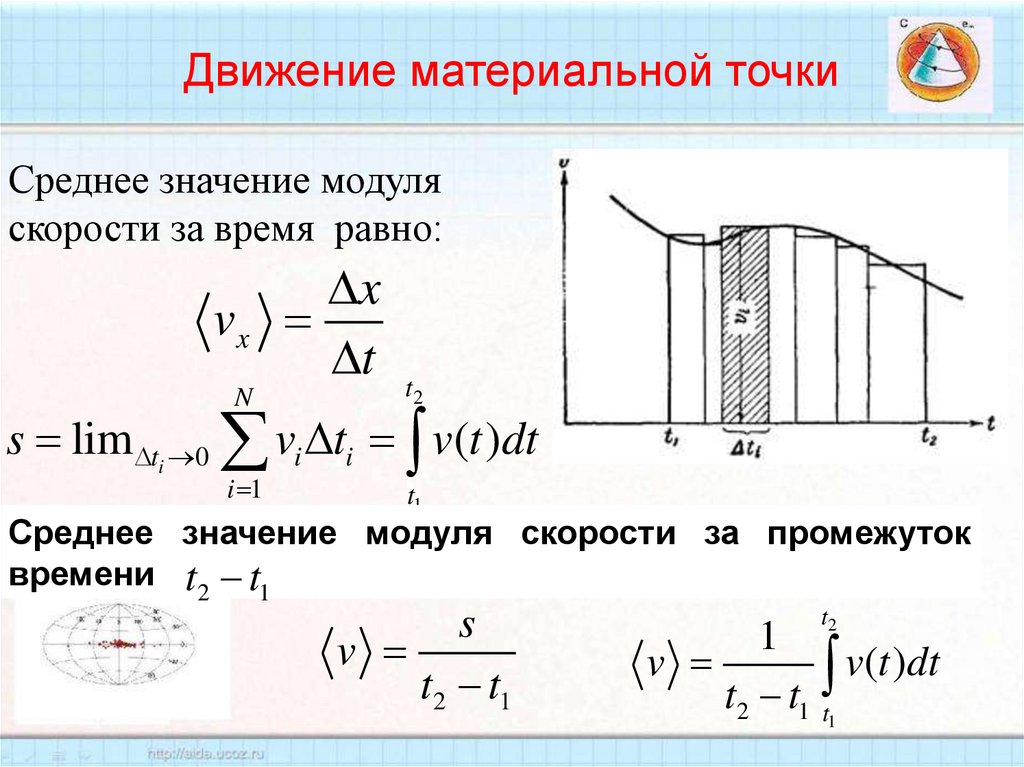
Среднее значение модуля
скорости за время равно:
x
vx
t t
N
2
s lim ti 0 vi ti v(t )dt
i 1
t1
Среднее значение модуля скорости за промежуток
времени t2 t1
s
v
t2 t1
t2
1
v
v(t )dt
t2 t1 t1

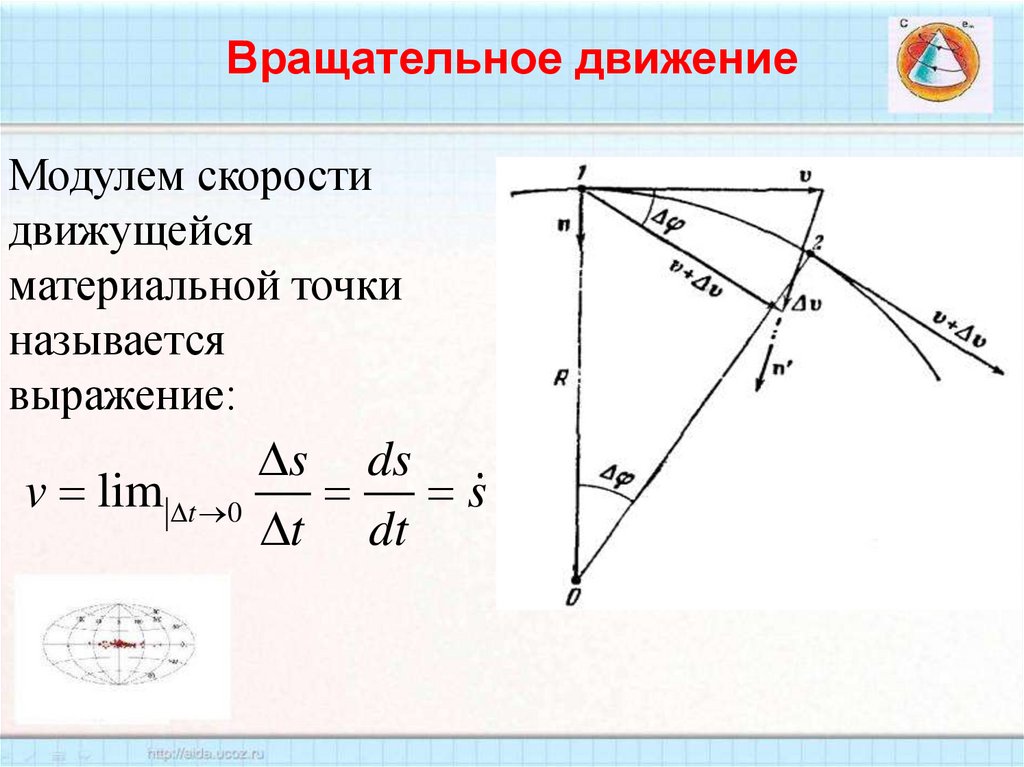
8. Вращательное движение

Модулем скорости
движущейся
материальной точки
называется
выражение:
s ds
v lim t 0
s
t dt

9. Ускорение

Вектор ускорения можно представить в виде
суммы двух векторов: a at an
dv
где - at
et
dt
de t
an v
dt
касательное ускорение,
нормальное ускорение
d
C lim s 0
s ds

10.

Движение по окружности
d
lim t 0
t
dt
Модуль угловой скорости:
2
t
T
T
2
2
1
T 2
d
Модуль углового ускорения: lim t 0
t
dt

11. Равномерное вращение

Равномерное вращение характеризуется периодом Т .
Период это время, за которое точка совершает один
оборот на угол 2 .
2
Следовательно,
t
T
T
2
Из этого выражения получаем: 2
Частотой называется число оборотов в единицу
времени: 1
T 2
d
Модуль углового ускорения lim t 0
t
dt

12. Кинематические характеристики

Линейная
координата
Скорость
Ускорение
Поступательное
движение
Угловая
x
координата
Угловая
dx
v
скорость
dt
Угловое
dv d 2 x
a 2
ускорение
dt dt
Вращательное
движение
d
dt
d d 2
2
d dt

13. Законы классической механики

14.  Законы Ньютона:

Существуют такие системы отсчёта, называемые инерциальными,
относительно которых материальная точка при отсутствии внешних
воздействий сохраняет величину и направление
своей скорости неограниченно долго.
В инерциальной системе отсчёта ускорение, которое получает
материальная точка, прямо пропорционально равнодействующей всех
приложенных к ней сил и обратно пропорционально её массе.
Материальные точки попарно действуют друг на друга с силами,
имеющими одинаковую природу, направленными вдоль прямой,
соединяющей эти точки, равными по модулю и противоположными
по направлению:

15.

Первый закон Ньютона
Всякое тело находится в состоянии покоя или
равномерного и прямолинейного движения, пока
воздействие со стороны других тел не заставит его
изменить это состояние. Система отчета, в которой
выполняется этот закон, называется инерциальной.
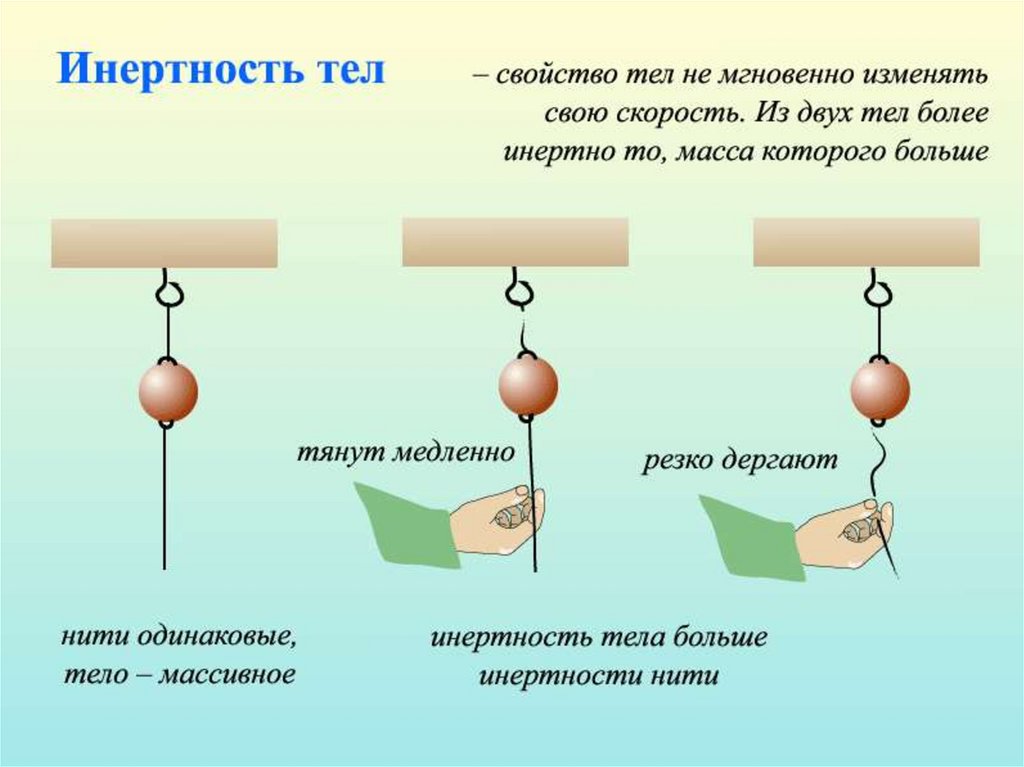
Масса – количественная характеристика инертности
тел.
Импульс материальной точки массой т, движущейся
со скоростью
: p mv
.

16. Первый закон Ньютона

Системы отсчета относительно
которых движущиеся тела
сохраняют свою скорость
постоянной, если на них не
действуют
другие
тела,
называются инерциальными.
Явление
сохранения
скорости движения тела (в
частности, состояние покоя)
при компенсации внешних
воздействий
на
тело
называют инерцией. Поэтому
первый закон Ньютона часто
называют законом инерции

17.

18.

19.

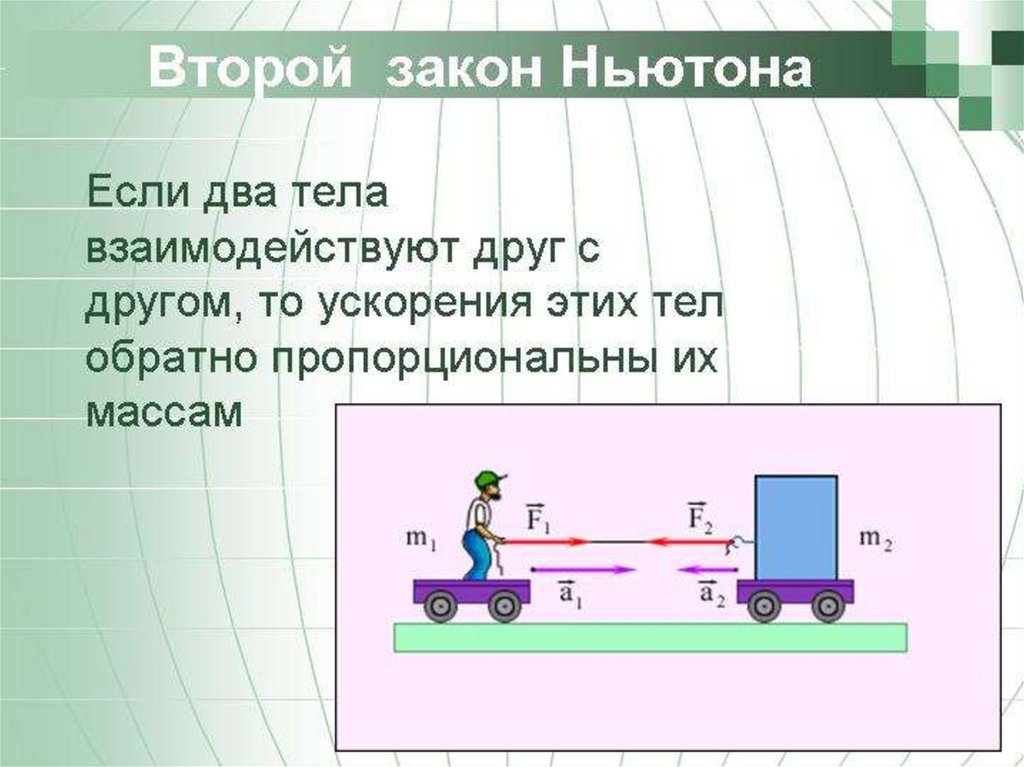
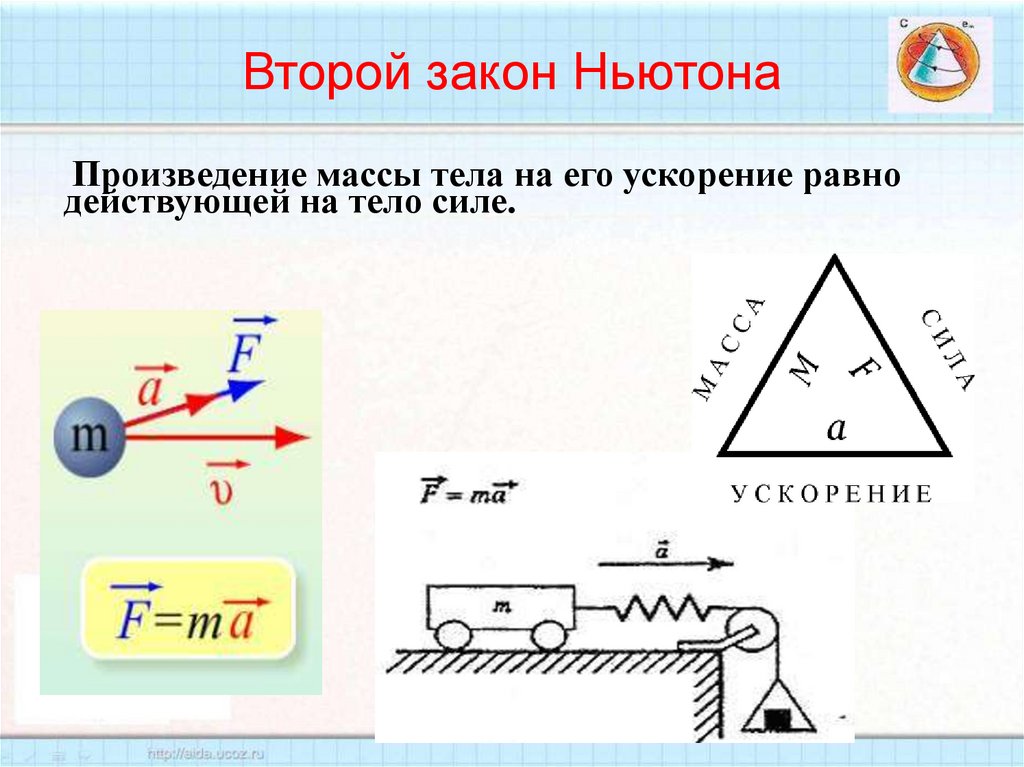
20. Второй закон Ньютона

Произведение массы тела на его ускорение равно
действующей на тело силе.

21.

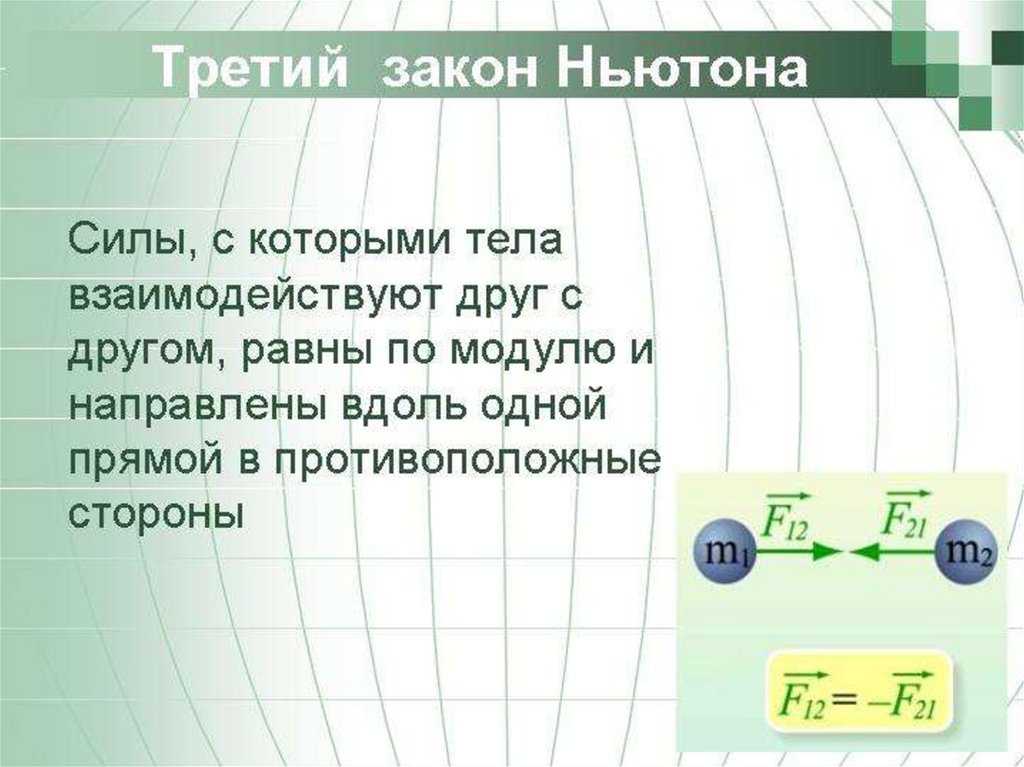
22. Третий закон Ньютона

Стоя на полу вы воздействуете на пол с силой,
пропорциональной массе вашего тела. Согласно третьему
закону Ньютона пол в то же время воздействует на вас с
абсолютно такой же по величине силой, но направленной
не вниз, а вверх.

23. Силы, рассматриваемые в механике

• а) сила упругости F kx
где k – коэффициент упругости (в случае пружины –
жесткость); х – абсолютная деформация;
p mg
• б) сила тяжести
• в) сила трения (скольжения)
F fN
где f - коэффициент трения; N - сила нормального давления.
m1m2
• г) сила гравитационного взаимодействия F
2
r
где - гравитационная постоянная; m1 ; m2 - массы
взаимодействующих тел;
- расстояние между телами
(тела рассматриваются как материальные точки).
r

24. Закон всемирного тяготения

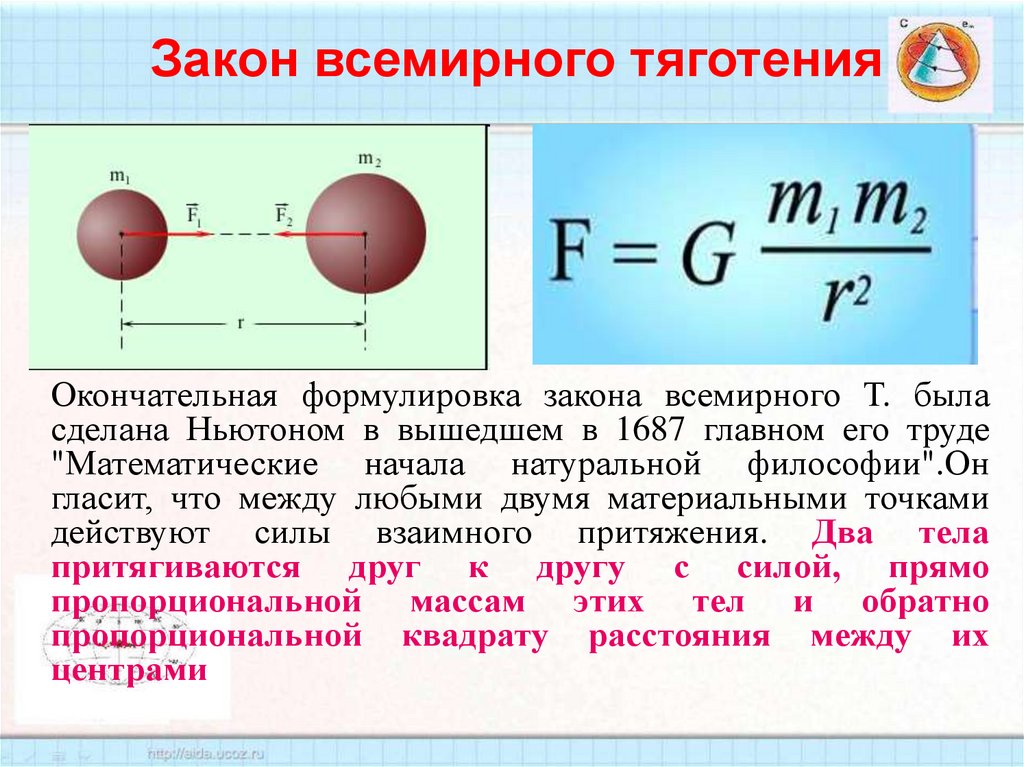
25. Закон всемирного тяготения

Окончательная формулировка закона всемирного Т. была
сделана Ньютоном в вышедшем в 1687 главном его труде
"Математические начала натуральной философии".Он
гласит, что между любыми двумя материальными точками
действуют силы взаимного притяжения. Два тела
притягиваются друг к другу с силой, прямо
пропорциональной массам этих тел и обратно
пропорциональной квадрату расстояния между их
центрами

26. Закон всемирного тяготения

Измерения Кавендиша методом крутильных весов
11
2
2
6.670
10
Н
м
кг
позволили получить значение
Напряженность гравитационного поля
F
G
m
U
Потенциал гравитационного поля
m
mM
U
r
A12 U1 U 2 m 1 2

27. Первая и вторая космическая скорость

Первая космическая скорость
v1 gRЗ 9.8 6.4 106 8 103 м с 8к м с
2
1
v
m
mg
RЗ
Вторая космическая скорость
2
M
m
mv
M Зm
З
2
mgR
A
mg
З
2
RЗ
2
RЗ
v2 2 gRЗ 2 8к м с 11к м с
Наличие Солнечной системы подтверждает притяжение
тел во Вселенной

28.

Закон всемирного тяготения
СВОЙСТВА СИЛ ВСЕМИРНОГО ТЯГОТЕНИЯ
1) СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ НАПРАВЛЕНА ВДОЛЬ ПРЯМОЙ, СОЕДИНЯЮЩЕЙ
МАТЕРИАЛЬНЫЕ ТОЧКИ, Т.Е. ЦЕНТРЫ МАСС ДВУХ ТЕЛ (ЭТИ СИЛЫ ЦЕНТРАЛЬНЫЕ)
2) ЭТО СИЛА ТОЛЬКО СИЛА ПРИТЯЖЕНИЯ
3) Т.К. ВЗАИМОДЕЙСТВУЮТ КАЖДЫЕ ИЗ ДВУХ ТЕЛ, ТО ПО ТРЕТЬЕМУ ЗАКОНУ НЬЮТОНА ОНИ
НАПРАВЛЕНЫ ВДОЛЬ ОДНОЙ ПРЯМОЙ И ПРОТИВОПОЛОЖНО НАПРАВЛЕНЫ
4) ЭТИ СИЛЫ ПРИЛОЖЕНЫ К РАЗНЫМ ТЕЛАМ, ПОЭТОМУ ОНИ НЕ МОГУТ ДРУГ ДРУГА
КОМПЕНСИРОВАТЬ
5) ПО ПРИРОДЕ ЭТИ СИЛЫ ГРАВИТАЦИОННЫЕ
6) ЭТИ СИЛЫ НЕЛЬЗЯ ЭКРАНИРОВАТЬ
7) ОНИ ДЕЙСТВУЮТ НА ЛЮБЫЕ ТЕЛА ВСЕЛЕННОЙ

29. Импульс

• Импульс тела (материальной точки) — векторная величина,
равная произведению массы тела (материальной точки) на её
скорость.
• Импульс системы тел (материальных точек) — векторная сумма
импульсов всех точек.
• Импульс силы — произведение силы на время её действия (или
интеграл по времени, если сила изменяется со временем).
• Изменение импульса системы материальных точек — в
инерциальной системе отсчета скорость изменения импульса
механической системы равна векторной сумме внешних сил,
действующих на материальные точки системы.
• Закон сохранения импульса: в инерциальной системе отсчета
импульс замкнутой системы сохраняется.

30. Вращательное движение твердого тела

При
вращательном
движении
все
точки
твердого тела движутся по
окружностям около оси
вращения.
Линейная
N
скорость v` точки с радиусвектором r , обусловленная
ma c Fi
вращением твердого тела,
i 1
v`
=
r.
Центр масс твердого тела равна
скорость
движется так, как двигалась бы Следовательно,
движения
этой
материальная точка с массой, сложного
равной
массе
тела,
под точки в неподвижной системе
действием всех приложенных координат имеет вид:
v = v0 + r.
сил.

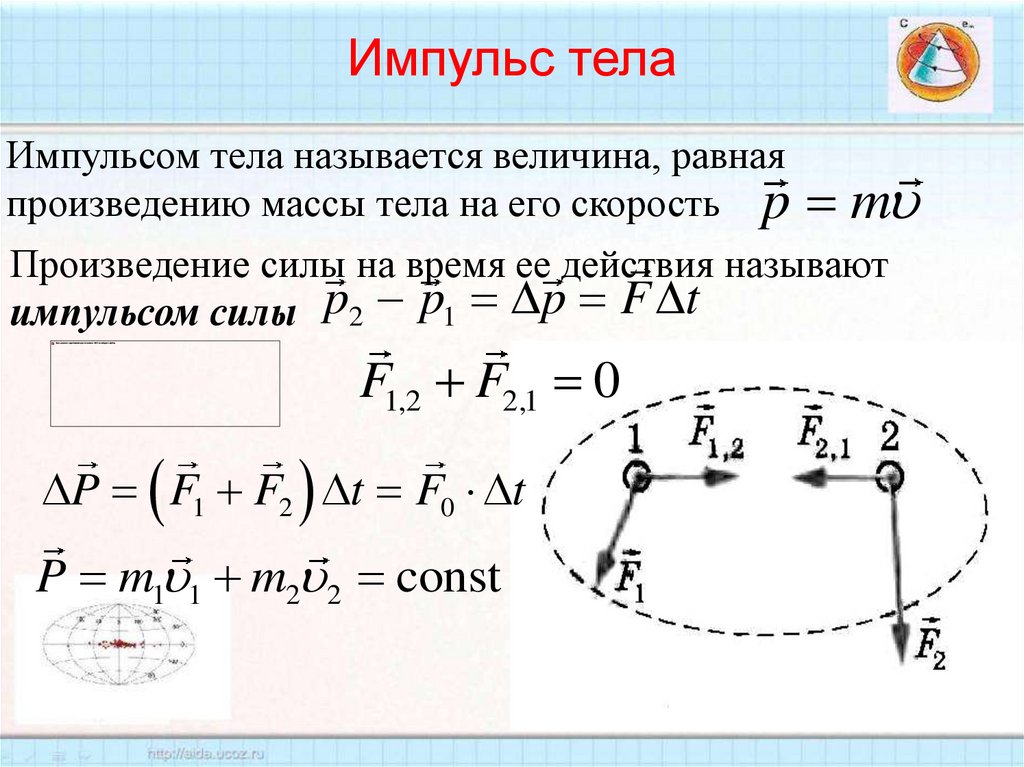
31. Импульс тела

Импульсом тела называется величина, равная
произведению массы тела на его скорость p m
Произведение силы на время ее действия называют
импульсом силы p2 p1 p F t
F1,2 F2,1 0
P F1 F2 t F0 t
P m1 1 m2 2 const

32.

Закон сохранения импульса
P m1 1 m2 2
n
mn n mi i const
m M V 0
m1 1 m1 1 m2 2
m
V
M
i 1

33. Основное уравнение динамики

mi R равная сумме произведений
Величина J
i
элементарных масс
на квадраты их расстояния от
некоторой оси, называется моментом инерции тела
относительно данной оси Lz J . Принимая во
внимание, что dLz M z ,получим основное уравнение
dt
динамики вращательного движения относительно
неподвижной оси : M z J z ,
где M z- результирующий момент внешних сил относительно оси , действующих на тело;
- угловое ускорение;
J - момент инерции относительно оси вращения
2
i
z

34. Законы сохранения в механике

.
Если на систему не действуют внешние силы, dp F
dt
dp
то
0 ,т.е. выполняется закон сохранения импульса
dt
Суммарный импульс замкнутой системы материальных
N
точек остается постоянным.
или для двух
p
const
i
i 1
тел
m1v1 m2 v 2 m1u1 m2u2
dL
M
dt
dL
При отсутствии внешних сил
0
dt
Следовательно, в замкнутой системе выполняется закон
N
сохранения момента импульса.
L const
i 1
i

35. Теорема Штейнера

Момент инерции J c относительно произвольной оси равен сумме
момента инерции J c относительно оси, параллельной данной и
проходящей через центр масс тела, и произведения массы m тела
на квадрат расстояния R между осями: J J mR 2
c
Поступательное
движение
Масса
m
Сила
F
Импульс p mv
Закон
dp
F
Ньютона
dt
ma F
Вращательное движение
Момент
инерции
Момент силы
Момент
импульса
J
M r F
L r p
Lz J
Закон
dL
M
динамики
dt
вращательного J M
z
движения

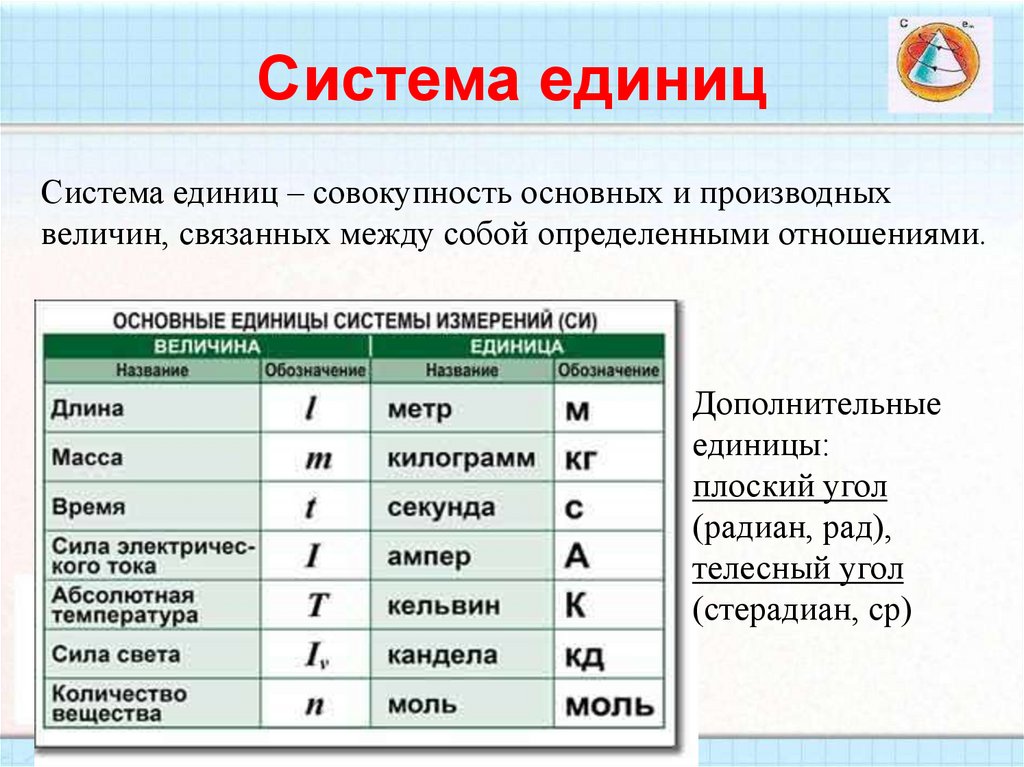
36. Система единиц

Система единиц – совокупность основных и производных
величин, связанных между собой определенными отношениями.
Дополнительные
единицы:
плоский угол
(радиан, рад),
телесный угол
(стерадиан, ср)

37.

Работа силы
Работу можно рассматривать как произведение проекции Fr на
модуль перемещения.Если на тело действует несколько сил, то
полная работа (сумма работ всех сил) равна работе
результирующей силы
p F t
A Fr r F r cos
Работа
силы
равна
произведению модулей силы
и
перемещения
точки
приложения
силы
и
косинуса угла между ними.
1 Дж = 1 Н 1 м = 1 Н м

38.

Мощность
Мощностью называют отношение работы A к интервалу времени
t, за который эта работа совершена: N A
r
N F cos F cos
t
t
Мощность равна 1 Вт, если работа
1 Дж совершается за 1 с.
В технической системе единиц работа часто измеряется в кгс м:
1 кгс м = 9,81 Дж;
1 Дж = 0,102 кгс м.,
поэтому мощность выражается в кгс м/с или лошадиных силах
(л.с.): 1 Дж 1Н 1м 105 дин 102 см 107 эрг; 1 Дж / с 1Вт 107 эрг / с
1 кгс м/с = 9,81 Вт;
1 л.с. = 75 кгс м/с = 75 9,81 Вт = 736 Вт.

39. Виды энергии

Механика различает
Потенциальную
энергию
( энергию
взаимодействия тел
между собой или с
внешними полями)
Кинетическую
энергию
(энергия движения).

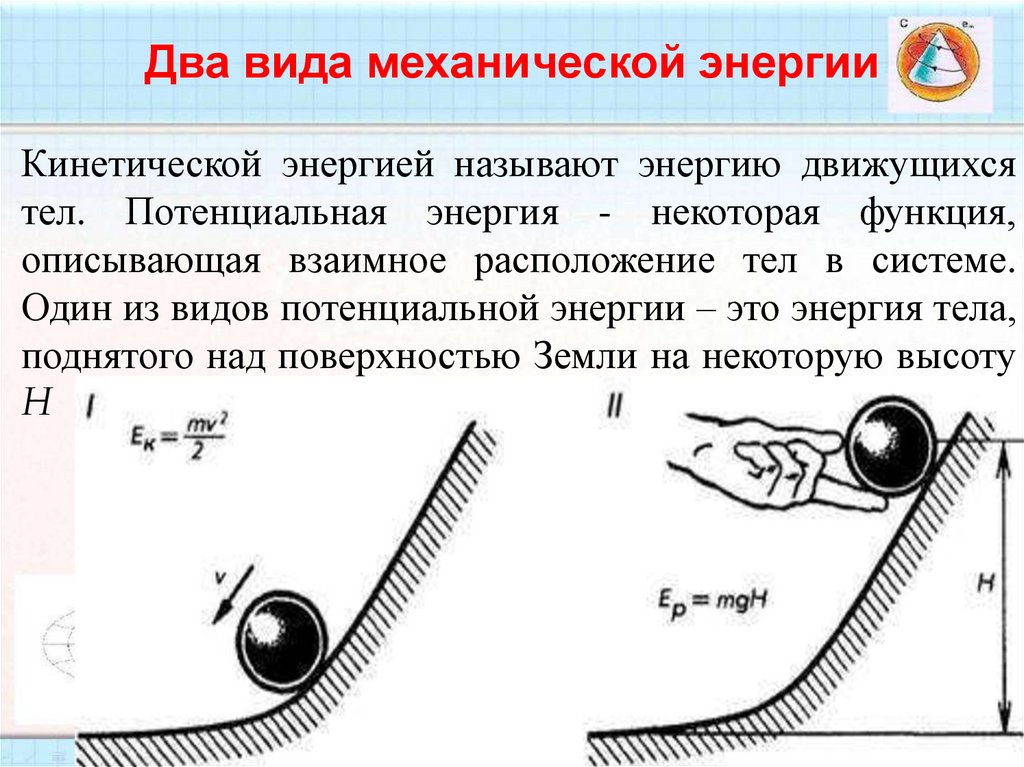
40. Два вида механической энергии

Кинетической энергией называют энергию движущихся
тел. Потенциальная энергия - некоторая функция,
описывающая взаимное расположение тел в системе.
Один из видов потенциальной энергии – это энергия тела,
поднятого над поверхностью Земли на некоторую высоту
H

41.

Кинетическая энергия — энергия механической системы,
зависящая от скоростей движения её точек.
Единица измерения в системе СИ — Джоуль.
Более строго, кинетическая энергия есть разность между
полной энергией системы и её энергией покоя; таким образом,
кинетическая энергия — часть полной энергии,
обусловленная движением.

42.

Потенциальная энергия — скалярная физическая величина,
характеризует запас энергии некоего тела (или материальной
точки), находящегося в потенциальном силовом поле, который идет
на приобретение (изменение) кинетической энергии тела за счет
работы сил поля.
Единицей измерения энергии в СИ является Джоуль.
A E p E p 0 E p
E p mgH

43.

Потенциальная энергия упруго деформированного
тела
Потенциальная
энергия упруго
деформированного
тела равна работе,
которую совершает
сила упругости при
переходе тела в
состояние, в
котором
деформация равна
нулю.
2
1
2
2
kx kx
A
E p 2 E p1
2
2

44. Коэффициент полезного действия

Коэффициентом полезного действия η— греческая буква
(«эта») машины называется отношение полезной
используемой энергии (полезной работы) Aпол к энергии,
подводимой к данной машине (затраченной работе) Aзат :
Aпол
Aзат
Aпол Aзат Апот
Коэффициент полезного действия можно определить
также отношением полезной мощности машины к
N пол
затраченной мощности двигателя:
N зат

45.

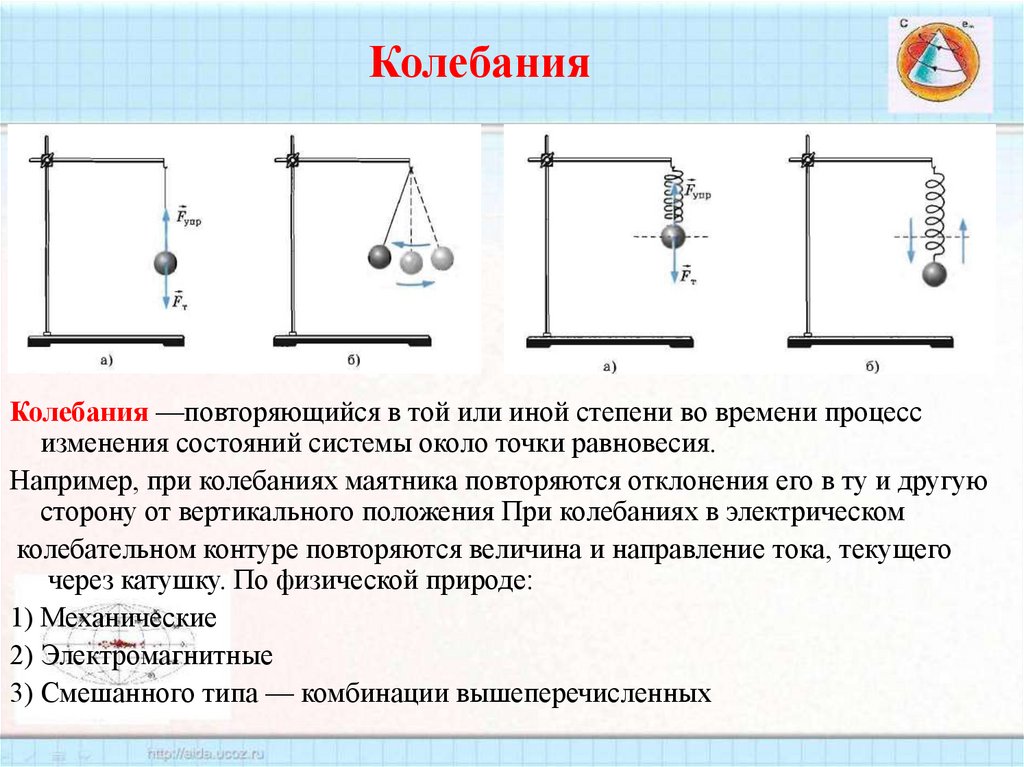
Колебания
Колебания —повторяющийся в той или иной степени во времени процесс
изменения состояний системы около точки равновесия.
Например, при колебаниях маятника повторяются отклонения его в ту и другую
сторону от вертикального положения При колебаниях в электрическом
колебательном контуре повторяются величина и направление тока, текущего
через катушку. По физической природе:
1) Механические
2) Электромагнитные
3) Смешанного типа — комбинации вышеперечисленных

46.

По характеру взаимодействия с окружающей
средой:
Свободные (или собственные) — это колебания в системе под действием внутренних сил,
после того как система выведена из состояния равновесия (в реальных условиях
свободные колебания всегда затухающие). Простейшими примерами свободных
колебаний являются колебания груза, прикреплённого к пружине, или груза,
подвешенного на нити.
Вынужденные — колебания, протекающие в системе под влиянием внешнего
периодического воздействия. Примеры: листья на деревьях, поднятие и опускание руки.
При вынужденных колебаниях может возникнуть явление резонанса: резкое
возрастание
амплитуды
колебаний
при
совпадении
собственной
частоты осциллятора и частоты внешнего воздействия.
Автоколебания — колебания, при которых система имеет запас потенциальной энергии,
расходующейся на совершение колебаний (пример такой системы — механические
часы). Характерным отличием автоколебаний от свободных колебаний является, то
что их амплитуда определяется свойствами самой системы, а не начальными
условиями.
Параметрические — колебания, возникающие при изменении какого-либо параметра
колебательной системы в результате внешнего воздействия.
Случайные — колебания, при которых внешняя или параметрическая нагрузка является
случайным процессом.

47.

Колебания, происходящие только благодаря начальному
запасу энергии, называются свободными колебаниями.
Свободные колебания всегда затухающие, так как весь
запас энергии, первоначально сообщенный
колебательной системе, в конце концов уходит на
совершение
работы
Колебания, совершаемые
телом под действием внешней
периодически изменяющейся силы, называются
вынужденными колебаниями. Вынужденные колебания незатухающие.

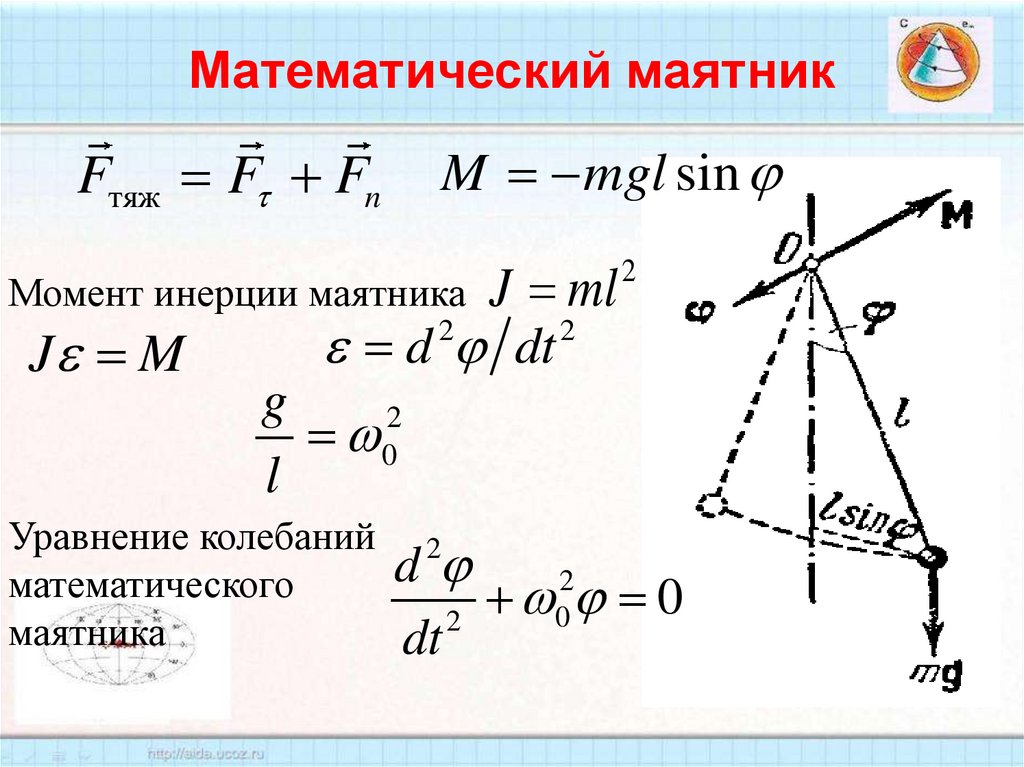
48. Математический маятник

Fтяж F Fn
M mgl sin
Момент инерции маятника J ml
J M
d dt
2
2
2
g
2
0
l
Уравнение колебаний 2
d
2
математического
0 0
2
маятника
dt

49. Физический маятник

,
Физический маятник
Вращательный момент сил M mgl sin
Уравнение динамики
2
d
вращательного
J 2 mgl sin
движения
dt
Колебания всех трех механических
систем описываются
дифференциальными уравнениями
одного и того же вида. Его решением
является кинематическое уравнение
гармонических колебаний
x(t ) A cos 0t

50. Соотношения в колебательной системе

Математический маятник
Период собственных колебаний
0
g
l
- собственная угловая или циклическая частота колебательной
системы
Физический маятник
Период собственных колебаний
Пружинный маятник
Период собственных колебаний
v A sin t , a A 2 cos t
x 2 x

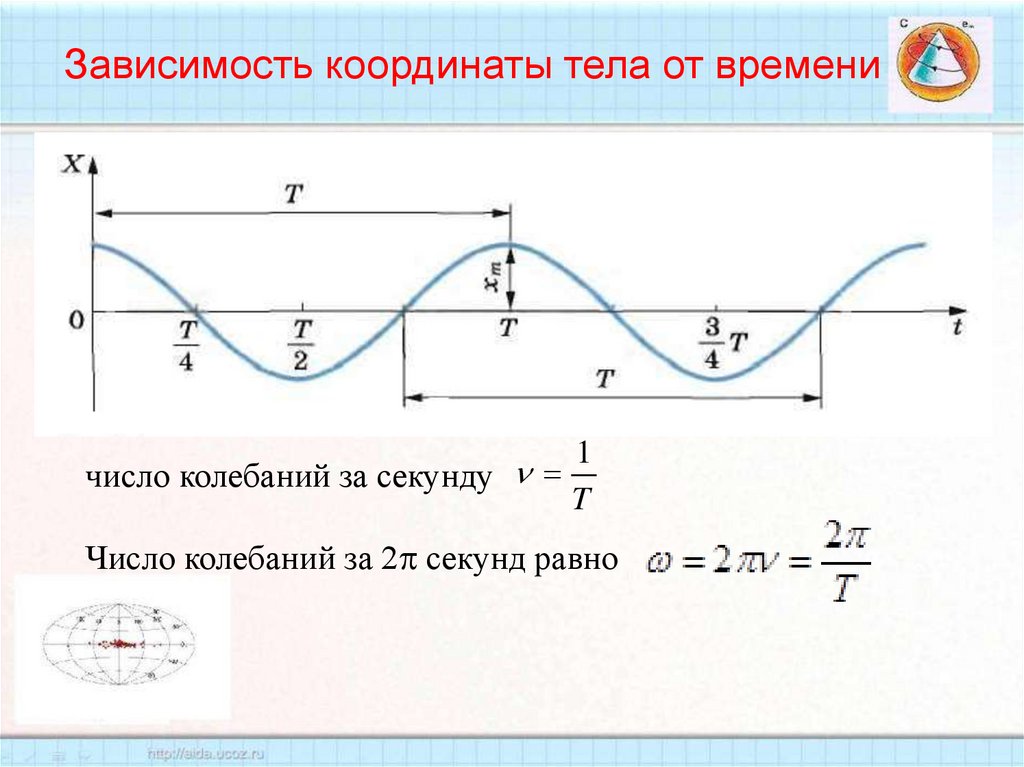
51. Зависимость координаты тела от времени

1
число колебаний за секунду
T
Число колебаний за 2 секунд равно

52.

Гармонические колебания
Это колебательные движения, при которых смещение тела
от положения равновесия совершается по закону синуса
или косинуса
Уравнение гармонического колебания
x = xm sin(ω0 t + φ0)

53. Амплитуда, период, частота колебаний

• А - амплитуда механических гармонических колебаний
- модуль наибольшего смещения колеблющегося
тела (материальной точки) от положения равновесия.
Единица измерения амплитуды – 1 метр.
• ω - круговая (циклическая) частота
• Т - период колебаний – время, за которое
колеблющееся тело совершит одно полное колебание
ν - частота (величина, обратная периоду) показывает,
сколько колебаний совершается за единицу времени

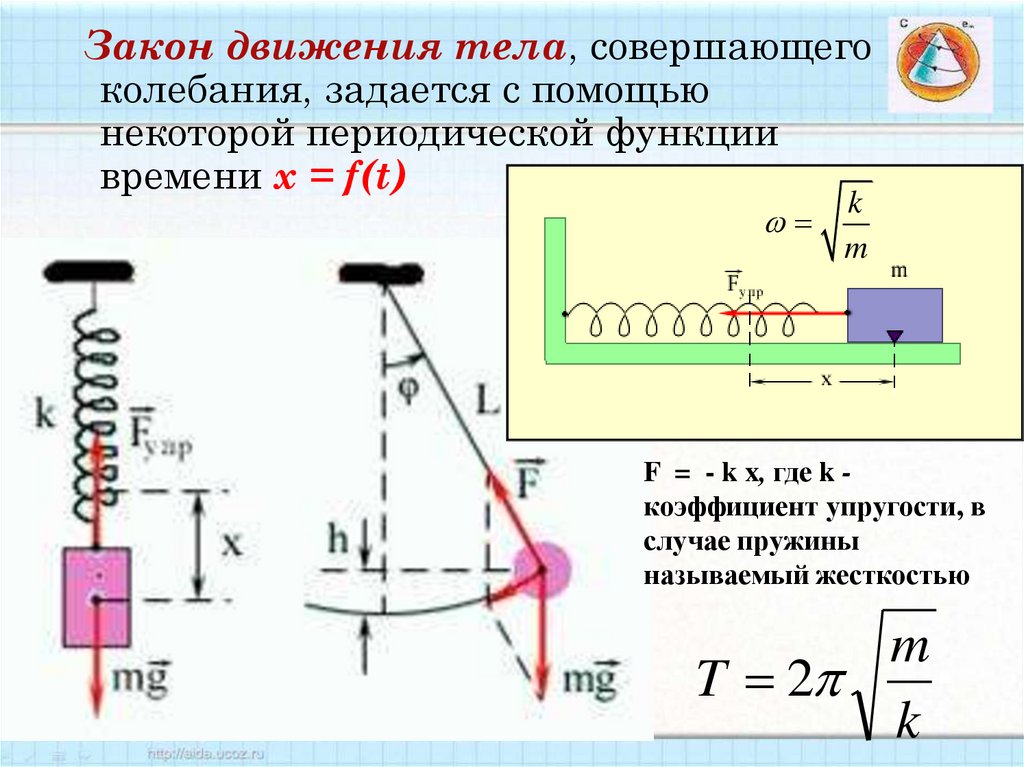
54.

Закон движения тела, совершающего
колебания, задается с помощью
некоторой периодической функции
времени x = f(t)
k
m
F = - k x, где k коэффициент упругости, в
случае пружины
называемый жесткостью
m
T 2
k

55. ФАЗА КОЛЕБАНИЙ

φ-фаза колебаний определяет состояние
колебательной системы в любой момент
времени. Фаза
указывает, сколько периодов
прошло от момента начала колебаний, а также
показывает при заданной амплитуде состояние
колебательной системы в любой момент времени
2 t
t
T
[φ] = радиан

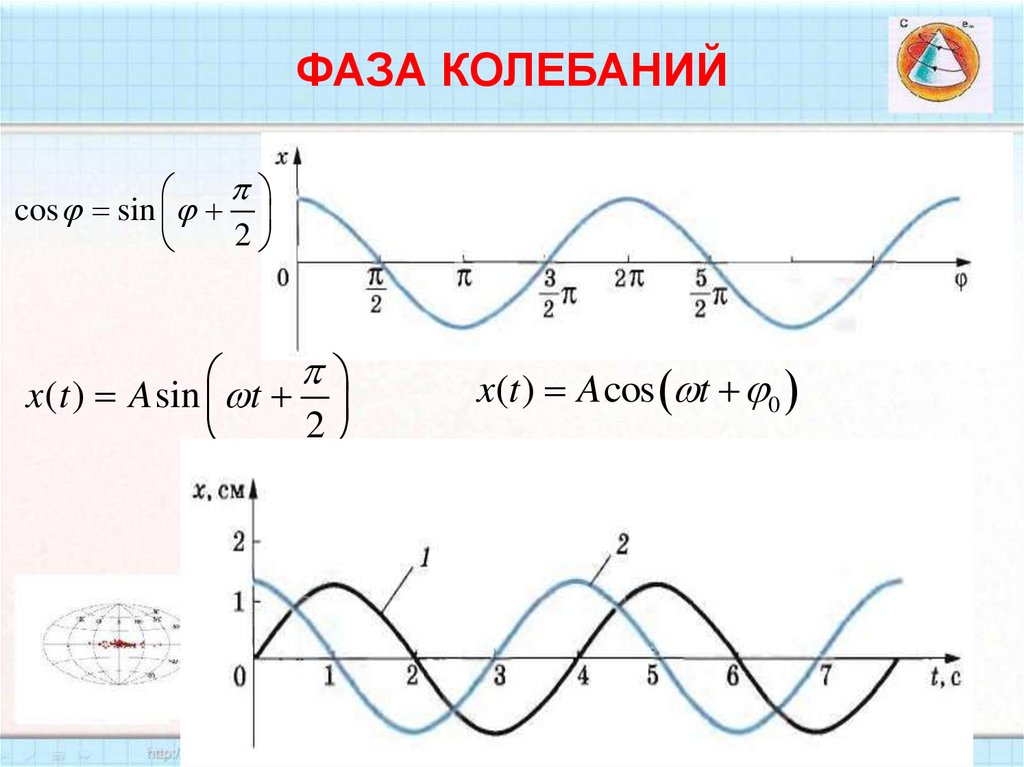
56. ФАЗА КОЛЕБАНИЙ

cos sin
2
x (t ) A sin t
2
x(t ) A cos t 0

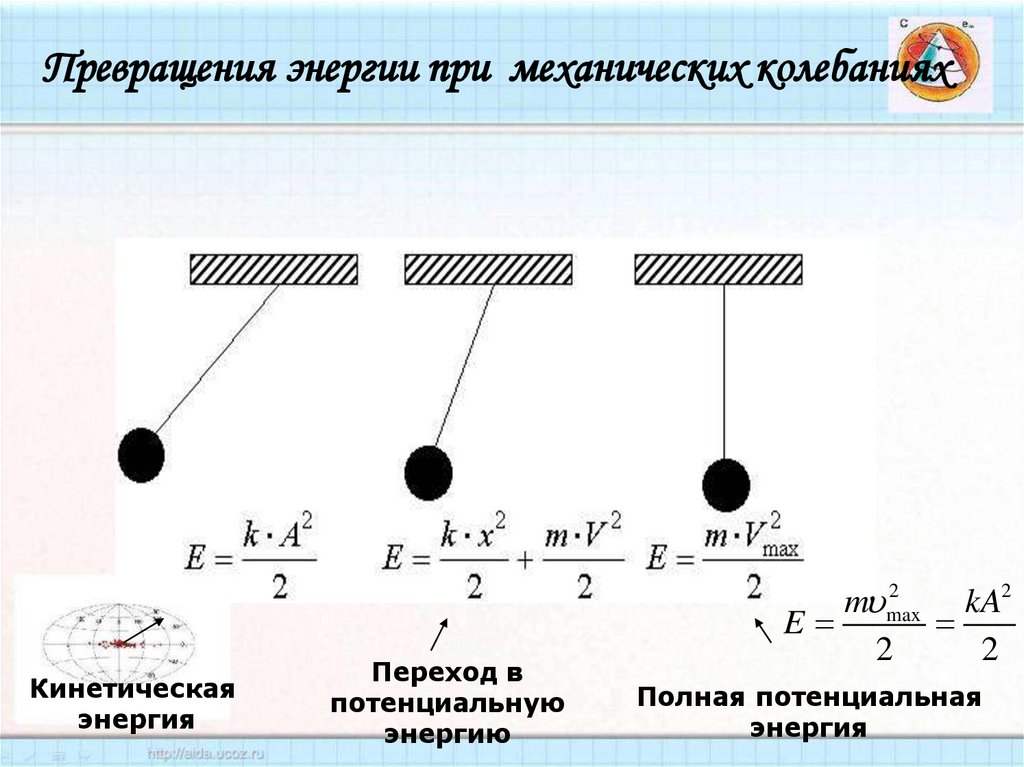
57.

Превращения энергии при механических колебаниях
Кинетическая
энергия
Переход в
потенциальную
энергию
2
m max
kA2
E
2
2
Полная потенциальная
энергия

58. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ

Затухающими
наз.
колебания,
энергия
(а
значит,
и
амплитуда)
которых уменьшается с
течением
времени.
Затухание
свободных
механических
гармонических колебаний
связано
с
убыванием
механической энергии за
счет
действия
сил
сопротивления и трения.

59.

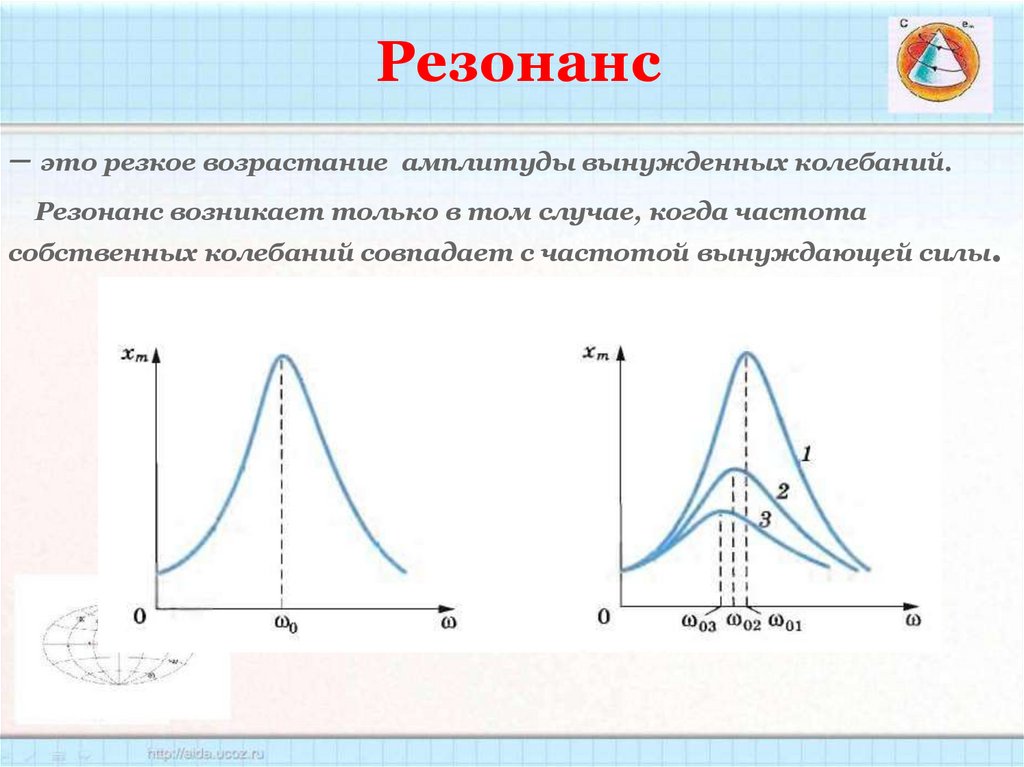
Резонанс
– это резкое возрастание амплитуды вынужденных колебаний.
Резонанс возникает только в том случае, когда частота
собственных колебаний совпадает с частотой вынуждающей силы.

60. Волна

Волна
—
изменение
состояния среды или физического
поля , распространяющееся либо
колеблющееся в пространстве и
времени
или
в
фазовом
пространстве. Другими словами,
«…волнами или волной называют
изменяющееся
со
временем
пространственное чередование
максимумов
и
минимумов
любой физической величины —
например, плотности вещества,
напряжённости электрического
поля, температуры».

61. Происхождение волн

Волны могут генерироваться различными способами.
1)Генерация локализованным источником колебаний.
2)Спонтанная генерация волн в объёме при
возникновении гидродинамических неустойчивостей.
Такую природу могут иметь, например, волны на
воде при достаточно большой скорости ветра,
дующего над водной гладью.
3)Переход волн одного типа в волны другого типа.
Например, при распространении электромагнитных
волн в кристаллическом твёрдом теле могут
генерироваться звуковые волны.

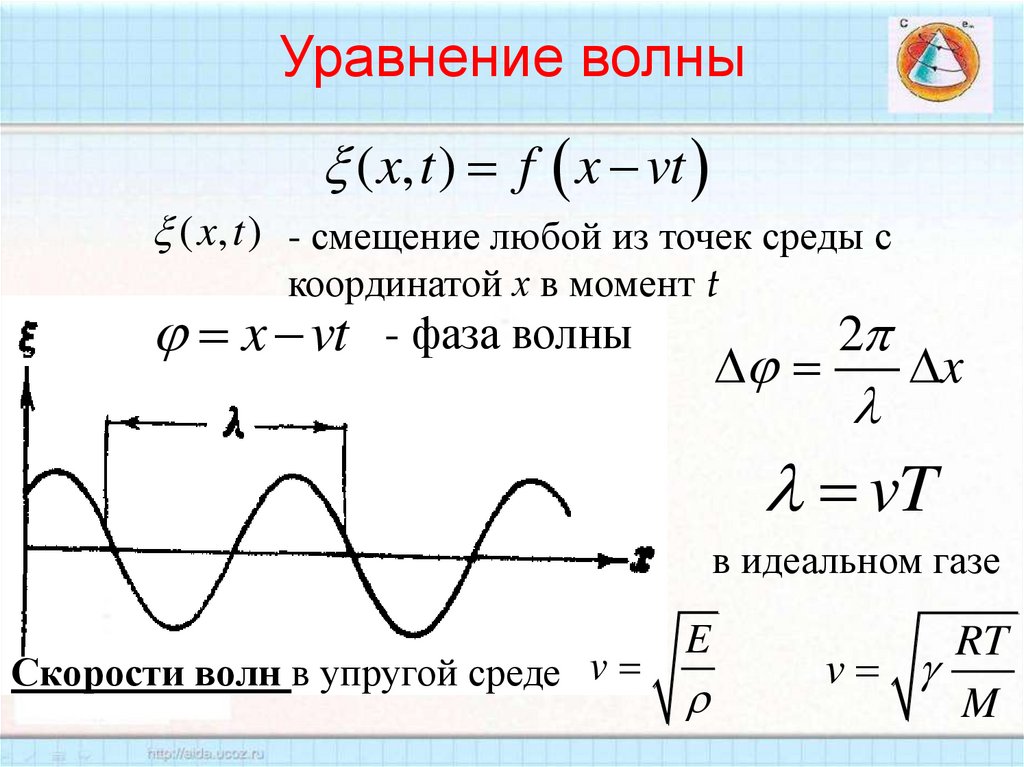
62. Уравнение волны

( x, t ) f x vt
( x, t ) - смещение любой из точек среды с
координатой х в момент t
x vt - фаза волны
2
x
vT
в идеальном газе
Скорости волн в упругой среде v
E
RT
v
M

63. Механические волны. Звук

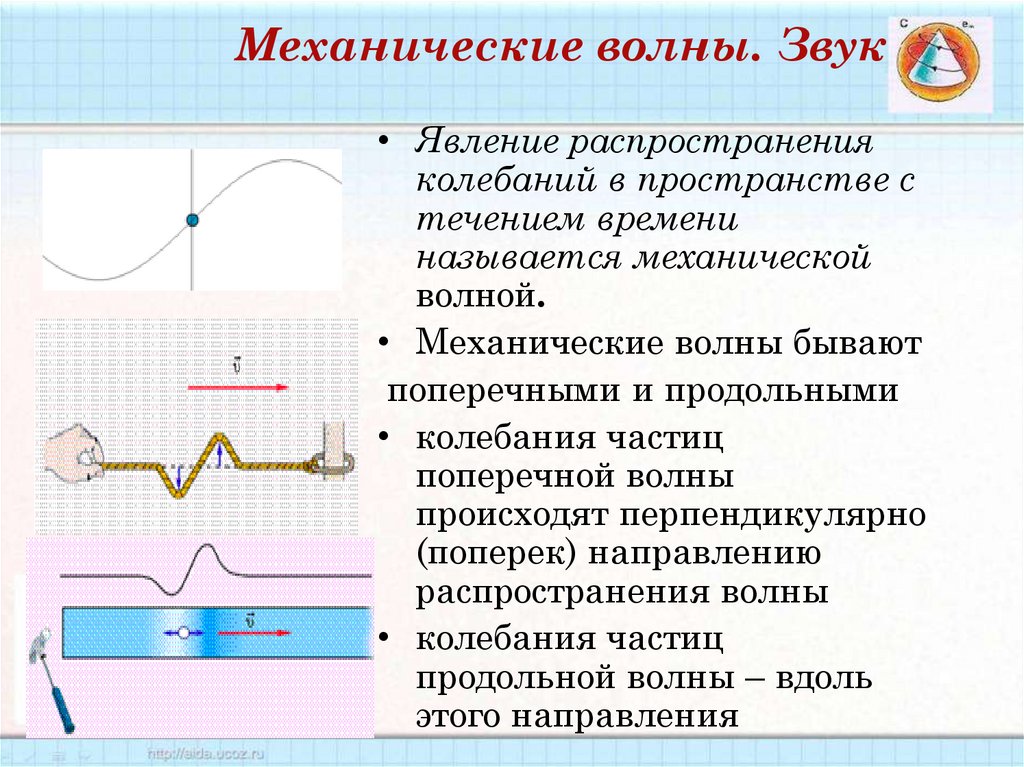
• Явление распространения
колебаний в пространстве с
течением времени
называется механической
волной.
• Механические волны бывают
поперечными и продольными
• колебания частиц
поперечной волны
происходят перпендикулярно
(поперек) направлению
распространения волны
• колебания частиц
продольной волны – вдоль
этого направления