Показникові нерівності

1.

Урок 05
Показникові нерівності
09.09.2022

2.

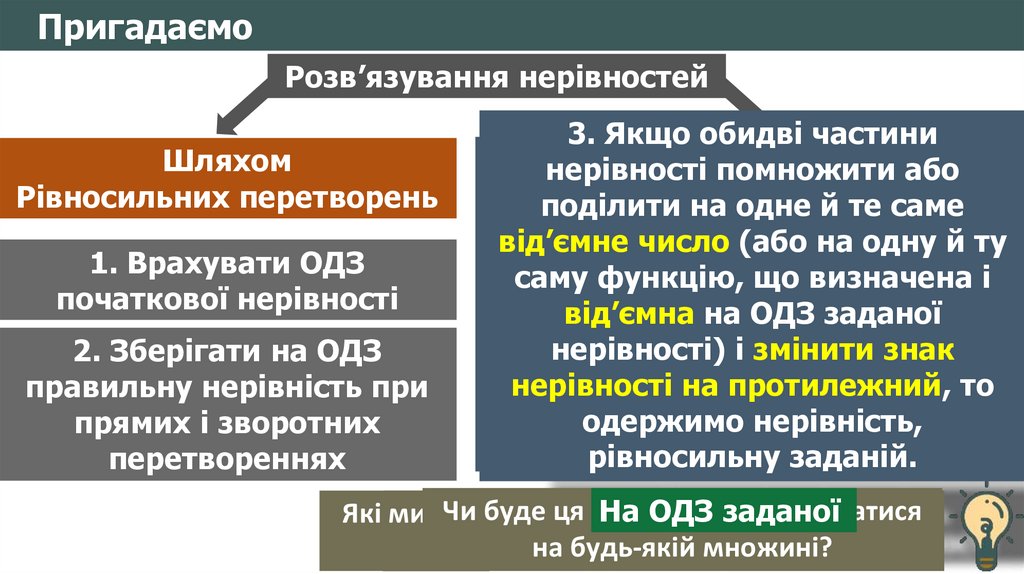
Пригадаємо
Розв’язування нерівностей
Шляхом
Рівносильних перетворень
1. Врахувати ОДЗ
початкової нерівності
2. Зберігати на ОДЗ
правильну нерівність при
прямих і зворотних
перетвореннях
3. Якщо обидві частини
2. Якщо зобидві
частини
Шляхом
1. нерівності
Якщо
однієї
частини
помножити
або
нерівності
помножити
абоіншу
нерівності
перенести
Методу
інтервалів
поділити
на
одне
й те в
саме
поділити
на одне
й
саме
частину
доданки
з протилежним
від’ємне
число
(або
нате
одну
й ту
1. Знайти
ОДЗ
додатне
число
(або
на
одну й ту
знаком,
то
одержимо
нерівність,
саму функцію, що визначена
і
саму
функцію,
рівносильну
заданій.
від’ємна
на що
ОДЗвизначена
заданої і
додатна наіОДЗ
заданої
нерівності)
змінити
знак
нерівності),
непротилежний,
змінюючи
На будь-якій
множині знак
нерівності
на
то
нерівності,
одержимо
одержимото
нерівність,
нерівність,
рівносильну
заданій.
рівносильну
заданій.
Чи У
буде
цяполягає
теорема
справджуватися
4.ОДЗ
Записати
відповідь,
На
заданої
Які ми
ЯкУсаме
вже
знаємо
ми
можемо
теореми
розв’язати
про
рівносильні
звичайну
чому
суть
методу
чому полягає суть методу
інтервалів?
враховуючи
знак нерівності
на будь-якій
множині?
перетворення
нерівність?
для перетворень?
нерівностей?
рівносильних

3.

Показникові нерівності
Показникові нерівності
місять змінну тільки у
показнику степеня
Найпростіші показникові
нерівності
Пригадайте теорему для показникових рівнянь. Чи буде
теорема для показникових нерівностей аналогічною?

4.

Показникові нерівності

5.

Показникові нерівності
Теорема

6.

Розв’язування показникових нерівностей
1
Метод
Методзведення
зведенняобох
обохчастин
частинрівняння
нерівності
до
достепенів
степенівз зоднаковими
однаковимиосновами
основами
2
Метод уведення нової змінної
3
Функціонально-графічний метод
Чи можемо Пригадайте
ми користуватися
методами
методицими
розв’язування
Поясніть, у чому полягає суть кожного методу?
для розв’язуванняпоказникових
показниковихрівнянь
нерівностей?

7.

Розв’язуємо гуртом
1
Чи рівносильні нерівності:

8.

Розв’язуємо гуртом
2
Розв’яжіть нерівність:

9.

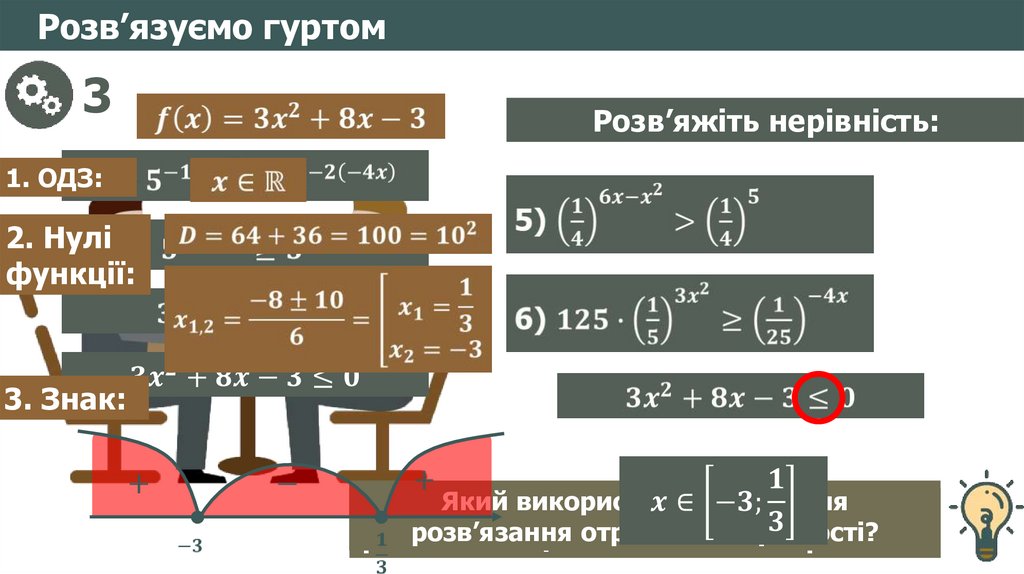
Розв’язуємо гуртом
3
Розв’яжіть нерівність:

10.

Розв’язуємо гуртом
3
Розв’яжіть нерівність:
Якщо дискримінант
квадратного тричлена
від’ємний, то даний тричлен
не можна розкласти на лінійні
множники
якою
формулою
можемо
розкласти
ЧиЗа
Які
завжди
будуть
можна
корені
розкласти
у цього
квадратного
квадратний
Які розв’язки
має ця нерівність?
Якійна
нерівності
рівносильна
множники
цей
квадратний
тричлен?
тричлен
рівняння
на
за
лінійні
теоремою
множники?
Вієта?

11.

Розв’язуємо гуртом
3
Розв’яжіть нерівність:

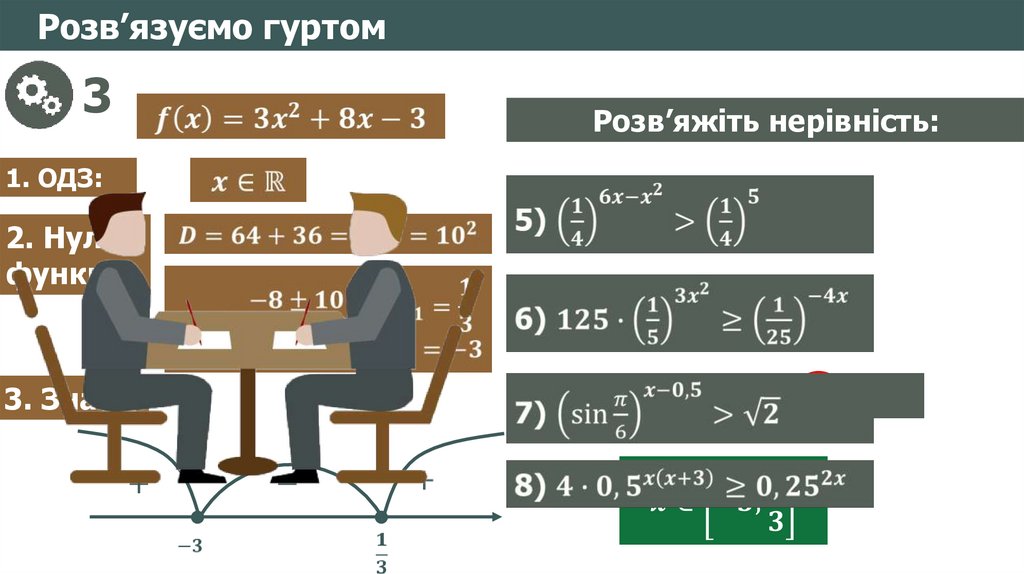
12.

Розв’язуємо гуртом
3
Розв’яжіть нерівність:
1. ОДЗ:
2. Нулі
функції:
3. Знак:
Який
Який використаємо
використаємо метод
метод для
для
розв’язання
нерівності?
розв’язання
цієї отриманої
показникової
нерівності?

13.

Розв’язуємо гуртом
3
1. ОДЗ:
2. Нулі
функції:
3. Знак:
Розв’яжіть нерівність:

14.

Розв’язуємо гуртом
4
Скільки цілих розв’язків має
нерівність:

15.

Розв’язуємо гуртом
5
Знайдіть область визначення
функції:

16.

Розв’язуємо гуртом
6
Розв’яжіть нерівність:

17.

Розв’язуємо гуртом
7
Розв’яжіть нерівність:

18.

Відповідаємо
Які нерівності називають показниковими?
Які нерівності називаються найпростішими показниковими
нерівностями?

19.

Домашнє завдання
Опрацювати §1 (ст.17-18)
Виконати № 3.3; 3.5(1-3); 3.7; 3.9; 3.11 (1,2);
3.13(1-2); 3.16
Мерзляк А.Г.
Опрацювати §3
Виконати № 3,2; 3,6; 3,10; 3,16
Істер О.С.
Опрацювати §2 (п.2.3)
Виконати № 2.3.1 (2,6,8); 2.3.2 (3,5,6);
Нелін Є.П.
Опрацювати §2 (ст.17)
Виконати № 71, 73, 77, 85, 88
Бевз Г.П.
09.09.2022
www.matnova.com.ua
Бажаю творчих успіхів!