AG_1_BI_Metod_Koordinat_Vect_An_Bez_Lin_Zavis

1. §1. МЕТОД КООРДИНАТ

АНАЛИТИЧЕСКАЯ
ГЕОМЕТРИЯ
§1. МЕТОД КООРДИНАТ
Аналитическая геометрия (АГ) – раздел математики, в
котором изучаются геометрические объекты по их уравнениям.

2. Математика — мощный и универсальный метод познания природы, образец для других наук. Рене Декарт

Математика — мощный и универсальный метод
познания природы, образец для других наук.
Рене Декарт
Основным методом АГ является метод координат. Метод введён
благодаря Декарту (1596– 1650)– французскому философу и
математику.
Метод координат
2

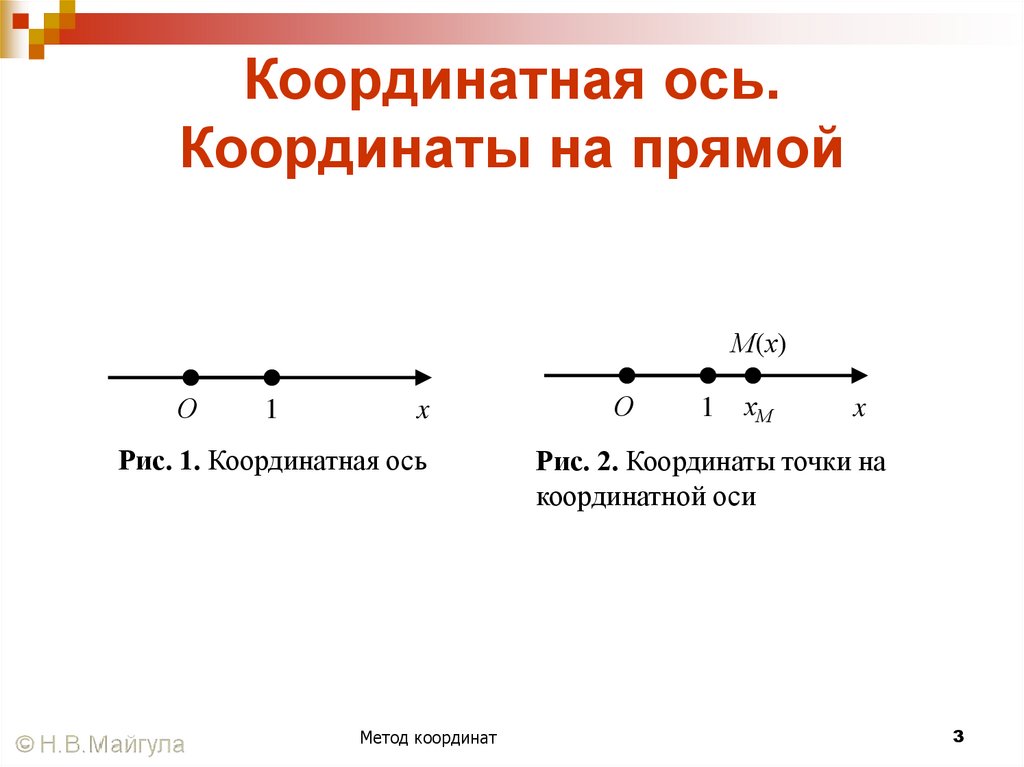
3. Координатная ось. Координаты на прямой

М(х)
О
1
x
Рис. 1. Координатная ось
Метод координат
О
1
хМ
x
Рис. 2. Координаты точки на
координатной оси
3

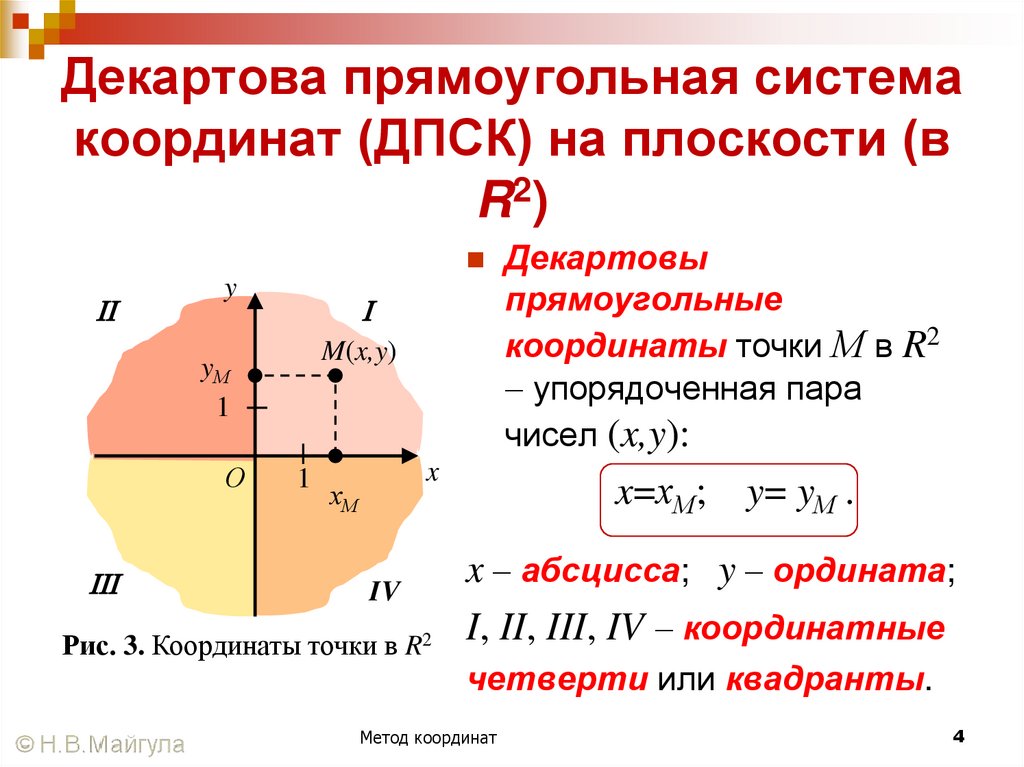
4. Декартова прямоугольная система координат (ДПСК) на плоскости (в R2)

y
M(x,y)
yМ
1
О
1
x
хМ
IV
Рис. 3. Координаты точки в R2
Декартовы
прямоугольные
координаты точки М в R2
упорядоченная пара
чисел (x,y):
x=хМ; y= yМ .
x абсцисса; y ордината;
I, II, III, IV координатные
четверти или квадранты.
Метод координат
4

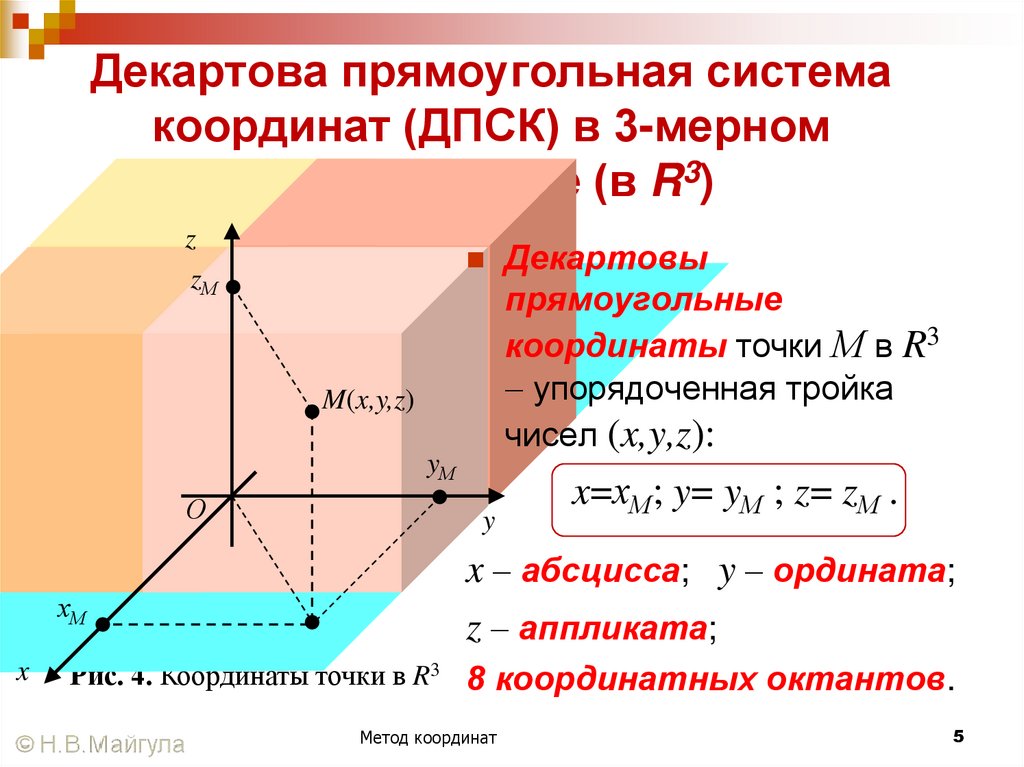
5. Декартова прямоугольная система координат (ДПСК) в 3-мерном пространстве (в R3)

z
zМ
M(x,y,z)
yМ
О
хМ
x
y
Декартовы
прямоугольные
координаты точки М в R3
упорядоченная тройка
чисел (x,y,z):
x=хМ; y= yМ ; z= zМ .
x абсцисса; y ордината;
z аппликата;
Рис. 4. Координаты точки в R3 8 координатных октантов.
Метод координат
5

6. Расстояние между точками

Точки А(хА) и В(хВ).
Расстояние между А и В:
( A, B) ( xB x A ) 2 xB x A .
Пример. Дано: точки А( 4) и В(3). Найдите расстояние
между А и В.
Решение. (А,В)=|хВ–хА|=3+4=7.
?
Метод координат
6

7.

Точки А(хА,yА) и В(хВ,yВ).
Расстояние между А и В:
( A, B) ( xB x A ) 2 ( y B y A ) 2 .
Пример. Дано: точки А(1, 2) и В( 3, 4).
Найдите 1) расстояние между А и В;
2) расстояние от А до начала координат.
Решение. 1) ( A, B)
2
3 1 2 ?
4 2 2 5;
2) (O, A) 12 22 5.
?
Метод координат
7

8.

Точки А(хА,yА,zА) и В(хВ,yВ,zB).
Расстояние между А и В:
( A, B) ( xB x A ) 2 ( y B y A ) 2 ( z B z A ) 2 .
Метод координат
8

9. Полярная система координат (ПСК)

О – полюс;
M( , )
+
О 1
Рис. 5. Полярная
система координат
Р
луч OP – полярная ось;
полярные координаты:
–
– полярный радиус,
0 ;
– полярный угол,
0 2π.
Метод координат
9

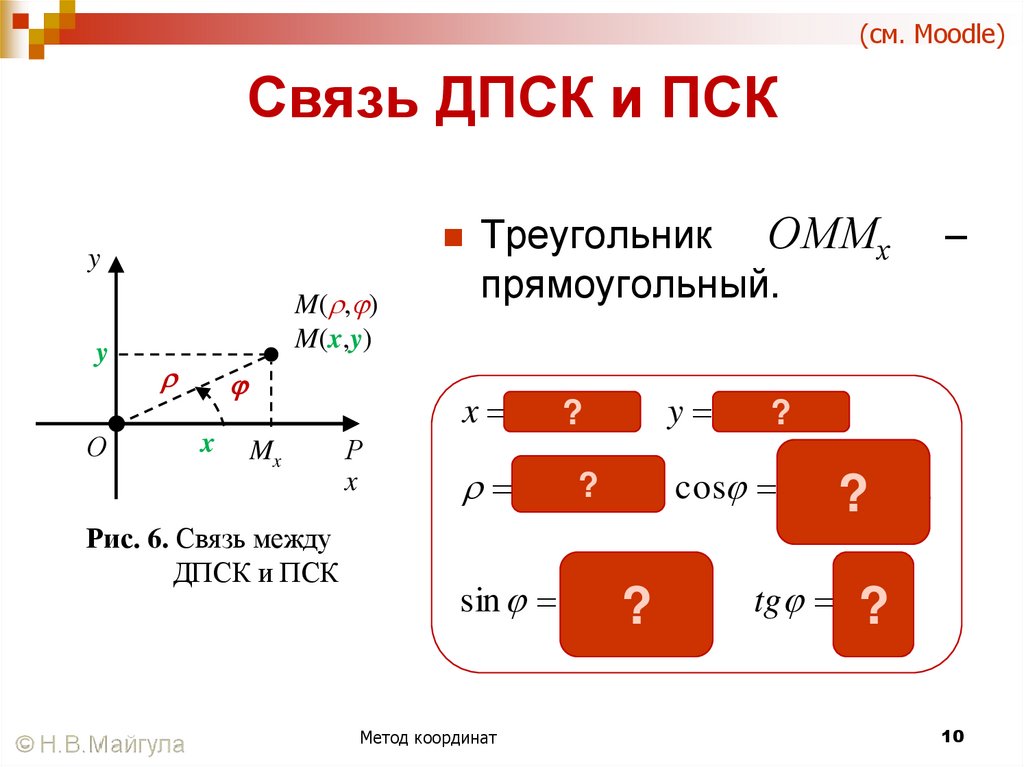
10. Связь ДПСК и ПСК

(см. Moodle)
Связь ДПСК и ПСК
Треугольник
y
y
О
M( , )
M(x,y)
x
ОММх
–
прямоугольный.
x cos
? ; y sin
? ;
Mx
Рис. 6. Связь между
ДПСК и ПСК
Р
x
x ? y ; cos
2
sin
Метод координат
2
y
;
?
2
x y
2
x
;
?
2
x y
2
y
tg ?
.
x
10

11. Пример. Дано: в ДПСК точка М(1; ). Найдите координаты точки М в ПСК.

Пример. Дано: в ДПСК точка М( 1; 3).
Найдите координаты точки М в ПСК.
y
Решение. Сделаем рисунок.
M
Ответ: М(2, ?2 /3).
3
Рисунок
1
О
Р
x
Метод координат
11

12. §2. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ

13. Основные определения

Вектор направленный отрезок
(упорядоченная пара точек).
Обозначение: АВ или AB – вектор с точкой
приложения А.
Нулевым называется вектор, начало и конец
которого совпадают. Обозначение: 0 или 0 .
Векторы, точка приложения которых может
быть выбрана произвольно, называются
свободными: a, b, или a , b.
Метод координат
13

14.

Длина или модуль вектора расстояние
между его началом и концом.
Единичным называется вектор, длина
которого равна 1.
Векторы называются коллинеарными, если
они параллельны одной прямой (в частности,
лежат на одной прямой).
Векторы называются компланарными, если
они параллельны одной плоскости (в
частности, лежат в одной плоскости).
Коллинеарные векторы всегда компланарны,
но не все компланарные векторы коллинеарны.
Метод координат
14

15. Линейные операции над векторами

1) Произведение вектора на число.
2) Сложение векторов.
Произведением вектора a на
действительное число t называется вектор,
обозначаемый t a или a t.
Длина этого вектора равна t а .
Направление совпадает с направлением вектора
a , если t>0, и противоположно ему, если t<0.
Метод координат
15

16. Пример. Дан вектор . Постройте векторы

Пример. Дан вектор a .
1
Постройте векторы 2a ; a .
3
Решение.
a
2a
Метод координат
1
a
3
16

17.

Сумма векторов
a1 , a2 ,..., an это вектор
n
с ai .
i 1
Начало вектора c находится в начале
первого вектора a1,
конец в конце последнего вектора an
ломаной линии, составленной из
последовательности слагаемых векторов.
Метод координат
17

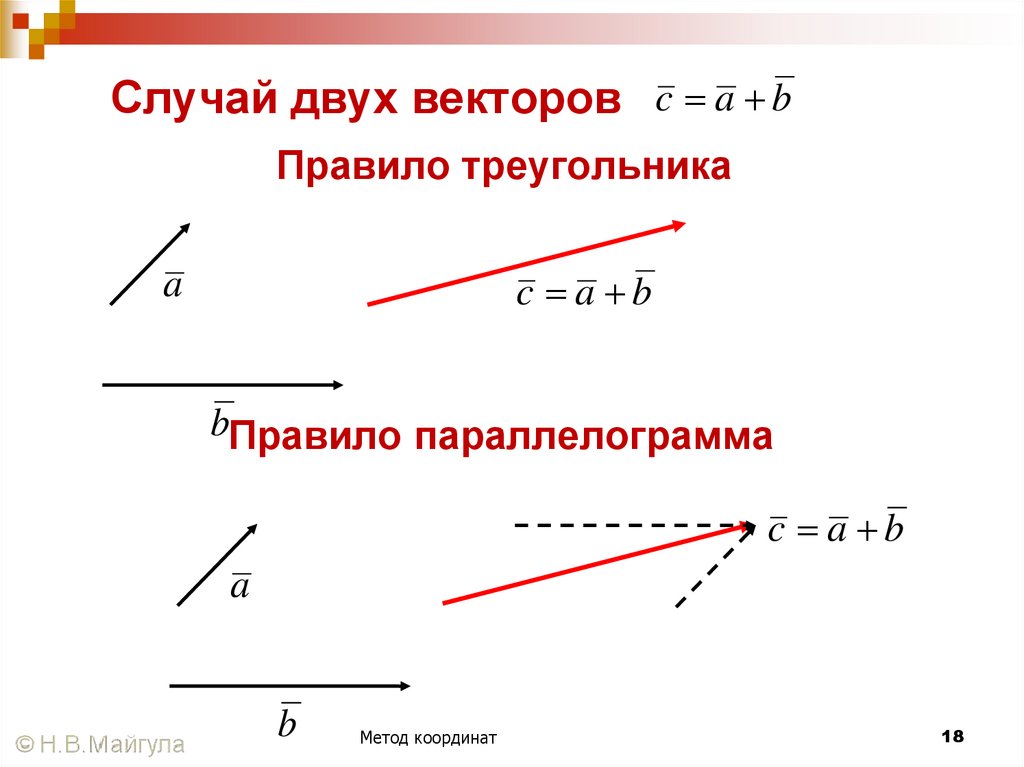
18. Случай двух векторов

c a b
Правило треугольника
c a b
a
bПравило параллелограмма
c a b
a
b
Метод координат
18

19.

Разность векторов
d a b a b
d a b
a
b
Метод координат
19

20.

Базисом на прямой называется любой
ненулевой вектор.
Базисом на плоскости называются любые 2
неколлинеарные вектора, взятые в
определенном порядке.
Базисом в пространстве называются любые
3 некомпланарных вектора, взятые в
определенном порядке.
Метод координат
20

21.

Если e1 , e2 , e3 - базис в пространстве и
a e1 e2 e3 ,
то числа , и - называются
компонентами или координатами вектора
в этом базисе.
Метод координат
21

22.

Базис называется ортонормированным,
если его векторы попарно ортогональны и их
длины равны единице.
Метод координат
22

23.

Пусть
i 1;0;0 , j 0;1;0 , k 0;0;1
– орты координатных осей ОХ, OY и OZ.
Разложение по базису
i , j, k вектора
a ( x, y , z ) :
a x i y j z k.
Метод координат
23

24. Пример 1. Дано: Представьте этот вектор в виде разложения по базису

Пример 1. Дано: a ( 3,0,1).
Представьте этот вектор в виде
разложения по базису i , j, k .
3i k .
Ответ: a ?
Метод координат
24

25. Координаты вектора. Простейшие действия над векторами, заданными своими координатами

Координаты вектора в R2
упорядоченная пара действительных
чисел x, y. Обозначение: a ( x, y ).
Аналогично в R3: a ( x, y , z ).
Перейти к примеру
Метод координат
25

26.

Рассмотрим точки А(хА,yА,zА) и В(хВ,yВ,zB).
AB ( xB x A , y B y A , z B z A ).
Пусть
a ( x, y, z ) и λ – действительное
число. Тогда вектор
c a ( x; y; z ).
Метод координат
26

27.

Пусть a ( x1 , y1 , z1 ) и
b ( x2 , y2 , z2 ). Тогда
с a b ( x1 x2 ; y1 y2 ; z1 z 2 );
d a b ( x1 x2 ; y1 y2 ; z1 z 2 ).
Метод координат
27

28. Пример 1. Дано: Найдите векторы

Пример 1. Дано: a (1,3); b ( 4,3); 2;
A(2, 1); B( 4;5).
Найдите векторы c a b ; d a b ;
e a ; AB .
Ответ:
c 3,6 ; d 5,0 ;
?
e 2,6 ; AB 6,6 .
Метод координат
28

29.

Пусть
a ( x, y, z ), точки А(хА,yА,zА) и
В(хВ,yВ,zB).
Тогда длина (модуль) вектора:
a
x y z ;
2
2
2
AB ( xB x A ) 2 ( y B y A ) 2 ( z B z A ) 2 .
Метод координат
29

30. Пример 2. Найдите длину векторов из примера 1. Найдите длину вектора

Пример 2. Найдите длину векторов a и AB из
примера 1.
3 1
; .
Найдите длину вектора b
2 2
Ответ: a 10;
AB 6 2, b 1, т.е. вектор
?
b является единичным.
Перейти к примеру 1
Метод координат
30

31.

Пусть a ( x1 , y1 , z1 ) и
b ( x2 , y2 , z2 ).
Если они коллинеарны, то
x1
y1 z 1
.
x2 y2 z 2
Метод координат
31

32. Пример 3. Дано: Коллинеарны ли эти векторы?

Пример 3. Дано: a (1,3); b ( 4,3).
Коллинеарны ли эти векторы?
Ответ: нет.
?
Метод координат
32

33. Деление отрезка в данном отношении

( ) М делит направленный отрезок
M 1M 2 в
отношении ( – некоторое число), если
выполняется равенство:
M 1M MM 2 .
Метод координат
33

34.

Пусть
M 1 ( x1 , y1 , z1 ); M 2 ( x 2 , y 2 , z 2 ); M ( x, y, z ).
Координаты точки М :
x1 x2
y1 y2
z1 z 2
xM
; yM
; zM
.
1
1
1
В частности, если ( ) М
(т.е. =1
?), то
середина отрезка
x1 x2
y1 y2
z1 z 2
xM
; yM
; zM
.
2
2
2
Метод координат
34

35. Пример. Дано: М1(–1;–2); М2(3;4). 1). На прямой (М1М2) найдите точку М, которая в 3 раза ближе к точке М1, чем к точке М2 и

находится вне направленного отрезка M 1M 2 .
2). Найдите середину этого отрезка.
Решение. Сделаем рисунок.
1).
Рисунок
1
M 1M ? MM 2 .
3
Указание: векторы M 1 M , MM 2
противоположнонаправленны.
Ответ: xM 3;
yM 5; N –?середина, x N 1;
Метод координат
y N 1.
35

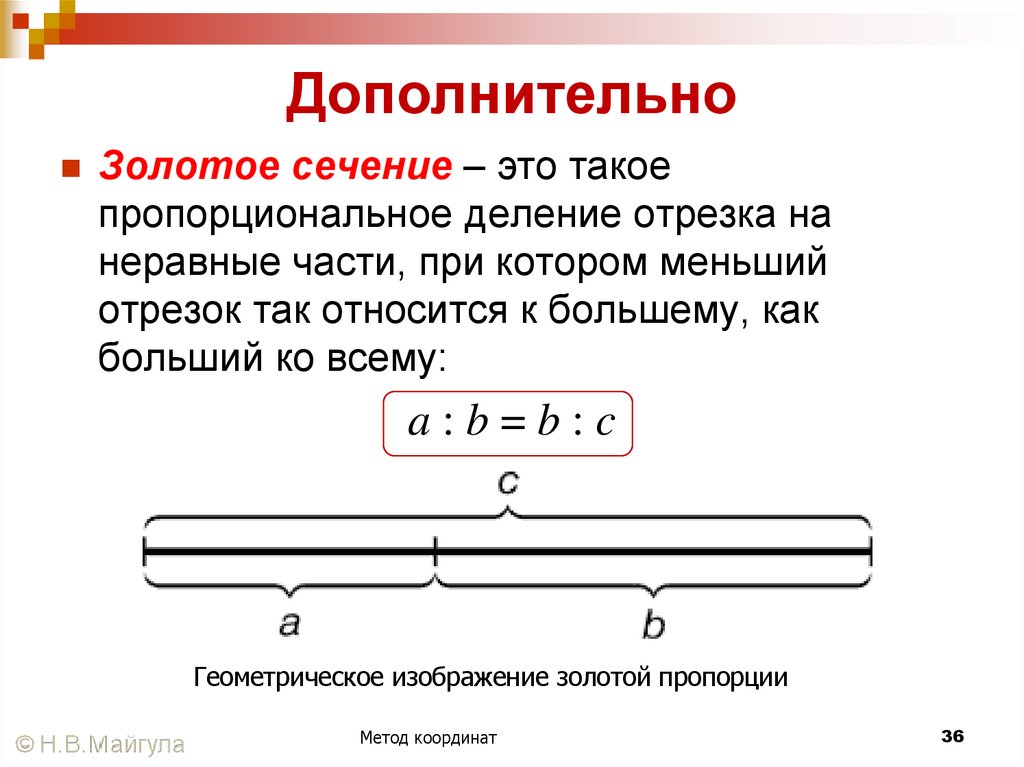
36. Дополнительно

Золотое сечение – это такое
пропорциональное деление отрезка на
неравные части, при котором меньший
отрезок так относится к большему, как
больший ко всему:
a:b=b:c
Геометрическое изображение золотой пропорции
Метод координат
36

37. Примеры.

Использование правила "Золотого сечения" расположение основных компонентов кадра в особых
точках - зрительных центрах.
Таких точек всего четыре, и расположены они на
расстоянии 3/8 и 5/8 от соответствующих краёв
плоскости. Человек всегда акцентирует своё
внимание на этих точках, независимо от формата
кадра или картины.
Метод координат
37

38.

Узнали картину? Леонардо да Винчи при написании этой
картины использовал правило золотого сечения.
У равнобедренных треугольников, выделенных на картине,
отношение основания к боковой стороне соответствует правилу
золотого сечения.
Метод координат
38

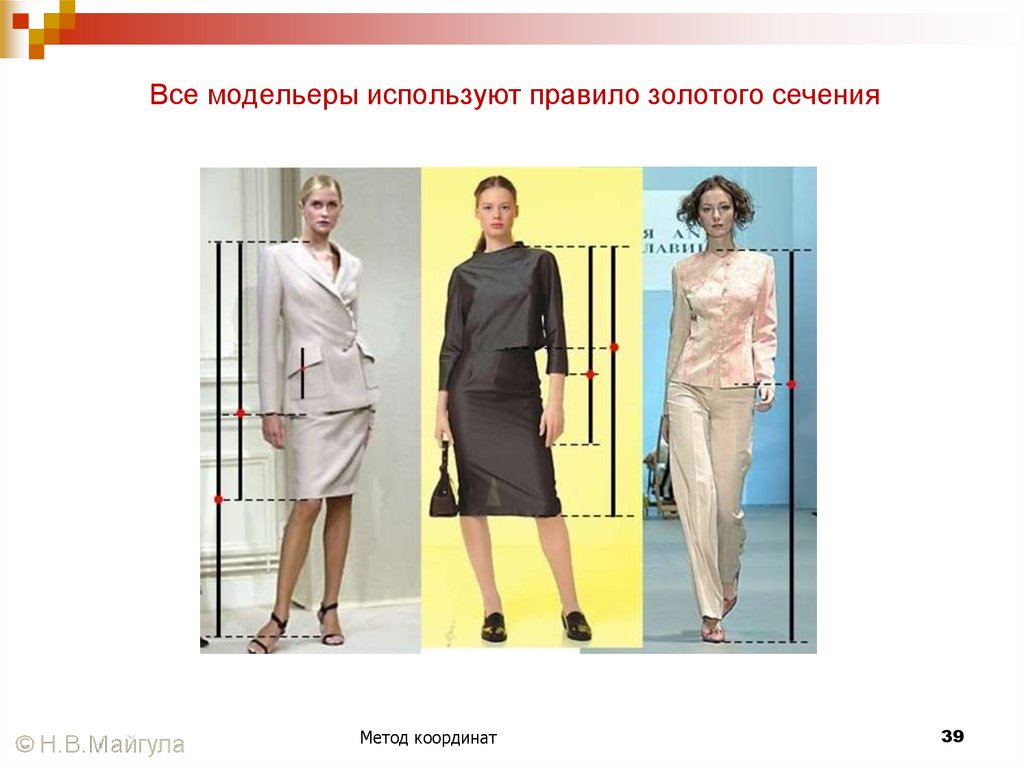
39.

Все модельеры используют правило золотого сечения
Метод координат
39

40.

По-вашему, где здесь золотое сечение?
Метод координат
40