Similar presentations:
Дроби обычные и десятичные
1. Дроби обычные и десятичные
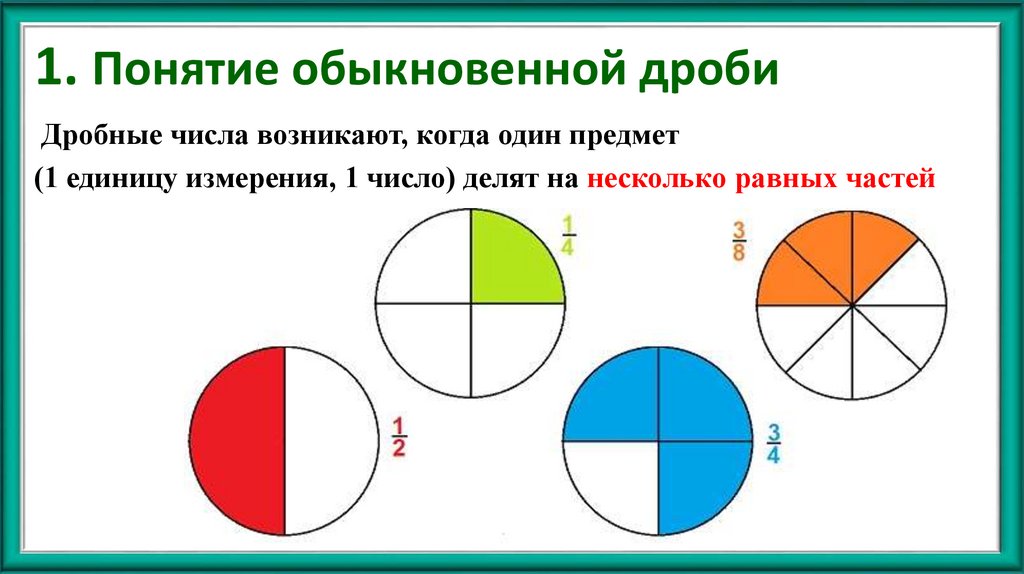
2. 1. Понятие обыкновенной дроби
Дробные числа возникают, когда один предмет(1 единицу измерения, 1 число) делят на несколько равных частей
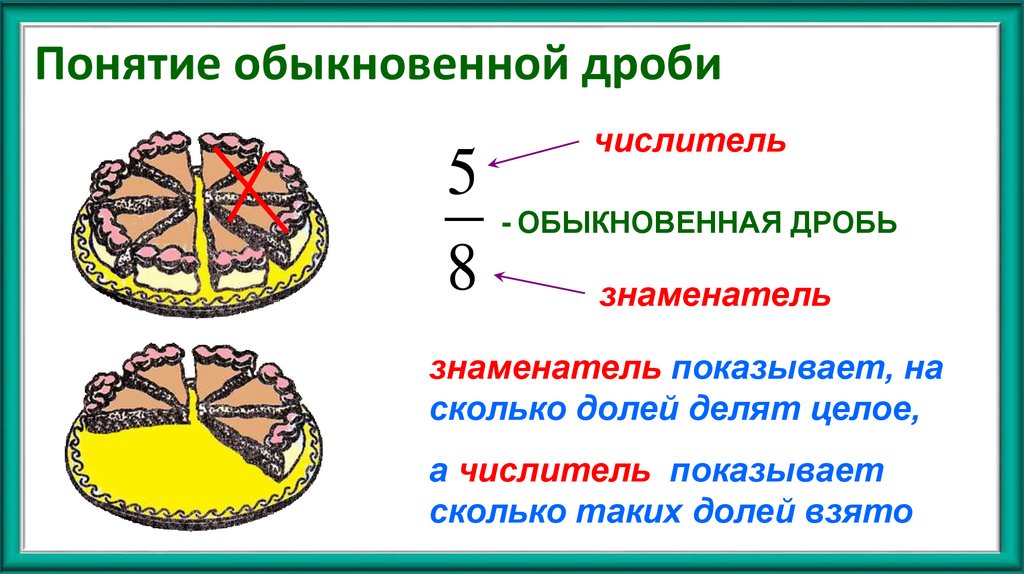
3. Понятие обыкновенной дроби
числитель5
- ОБЫКНОВЕННАЯ ДРОБЬ
8
знаменатель
знаменатель показывает, на
сколько долей делят целое,
а числитель показывает
сколько таких долей взято
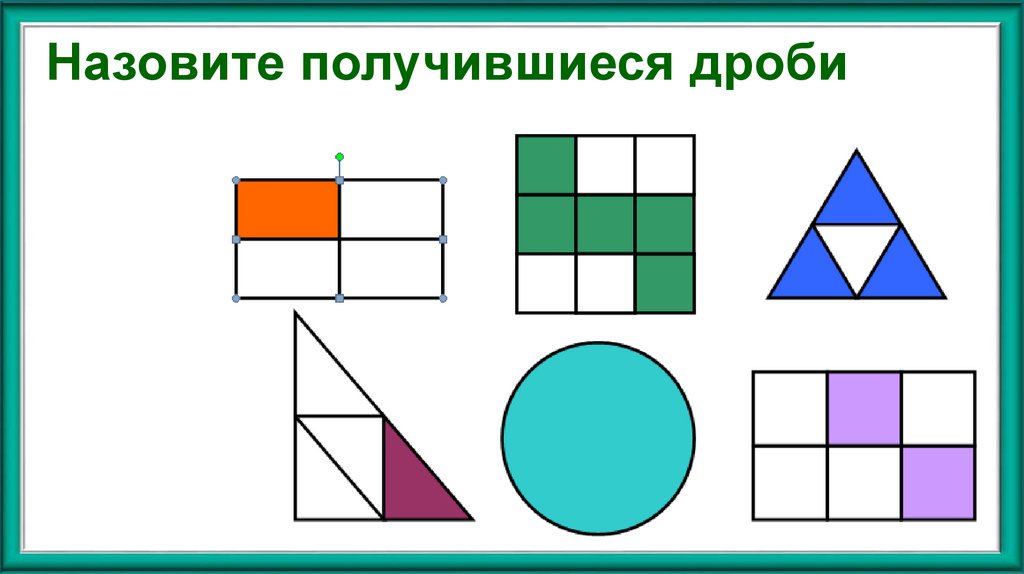
4. Назовите получившиеся дроби
5.
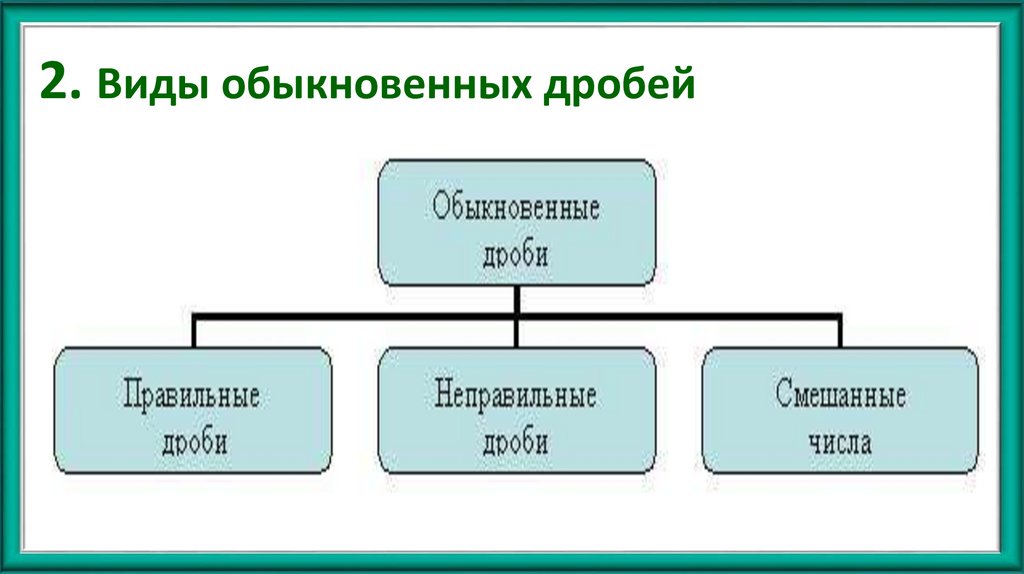
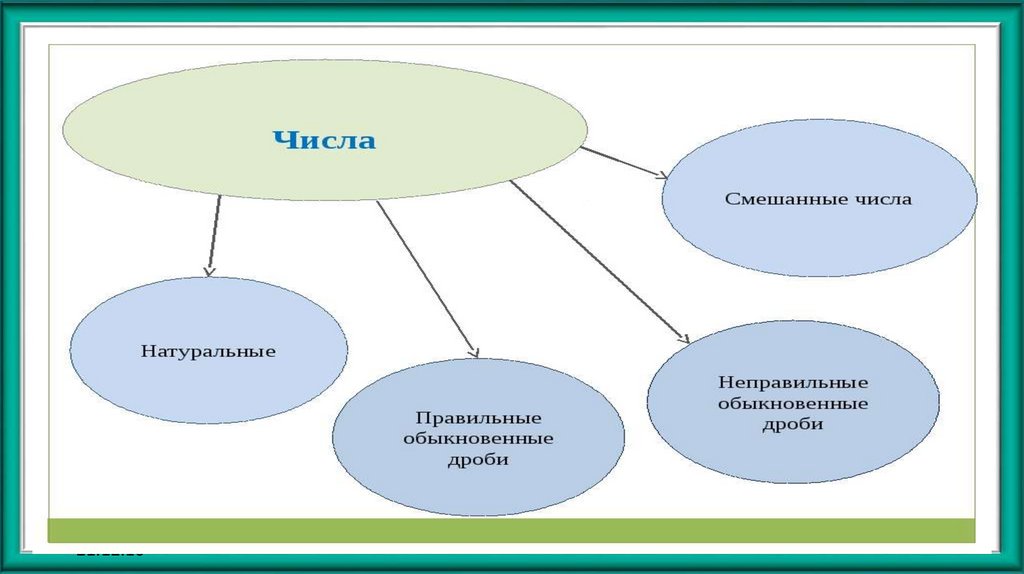
6. 2. Виды обыкновенных дробей
7. 2. Виды обыкновенных дробей
1).Если числитель дроби
меньше его
знаменателя, то такая
дробь называется
правильной
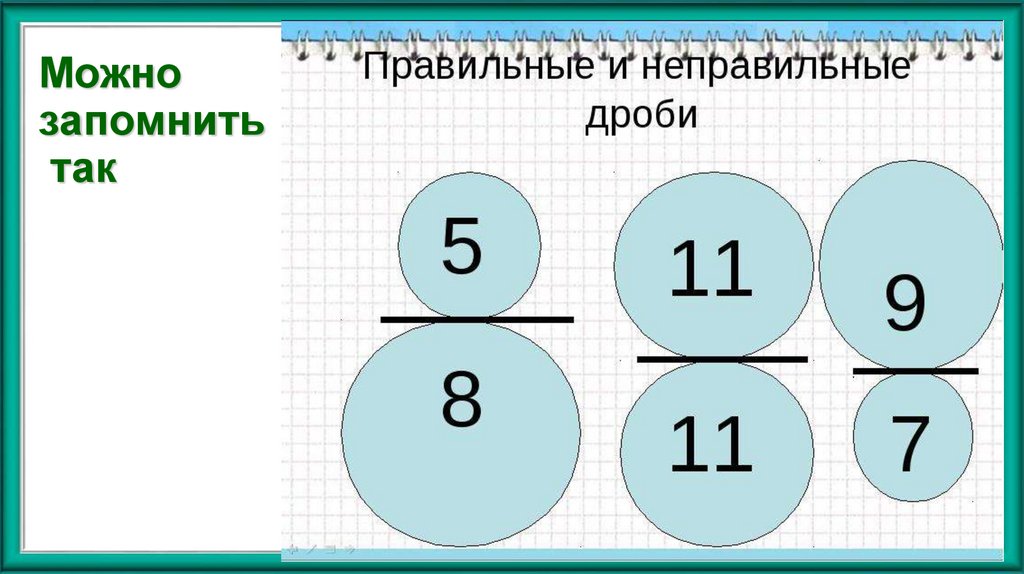
8. 2. Виды обыкновенных дробей
2).11
8
НЕПРАВИЛЬНАЯ ДРОБЬ –
это дробь, в которой
ЧИСЛИТЕЛЬ БОЛЬШЕ
ЗНАМЕНАТЕЛЯ
или РАВЕН ЕМУ
8 11
,
8 8
- НЕПРАВИЛЬНЫЕ ДРОБИ
9. Можно запомнить так
10. Запомним
11. Определите вид каждой дроби
12. ДРОБНЫЕ ЧИСЛА МОЖНО
СРАВНИВАТЬ,СКЛАДЫВАТЬ,
ВЫЧИТАТЬ,
УМНОЖАТЬ
и ДЕЛИТЬ
13. 3. Сравнение обыкновенных дробей
РассмотримЗначит: из двух дробей с одинаковыми
знаменателями та больше, у которой числитель
больше
и та меньше, у которой числитель меньше
14. 3. Сравнение обыкновенных дробей
РассмотримЗначит: из двух дробей с одинаковыми
числителями та дробь больше, у которой
знаменатель меньше
15. Запомним
• Все правильные дроби меньшеединицы, а
неправильные – больше или равны единице.
3
8
11
1,
1,
1
8
8
8
• Каждая неправильная дробь больше любой
правильной дроби, а каждая правильная дробь
меньше любой неправильной дроби
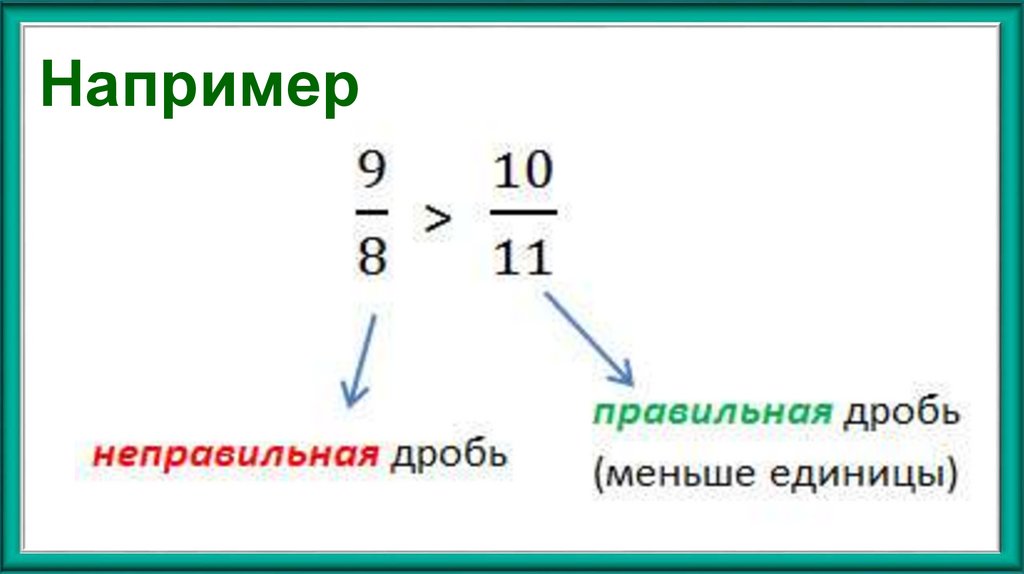
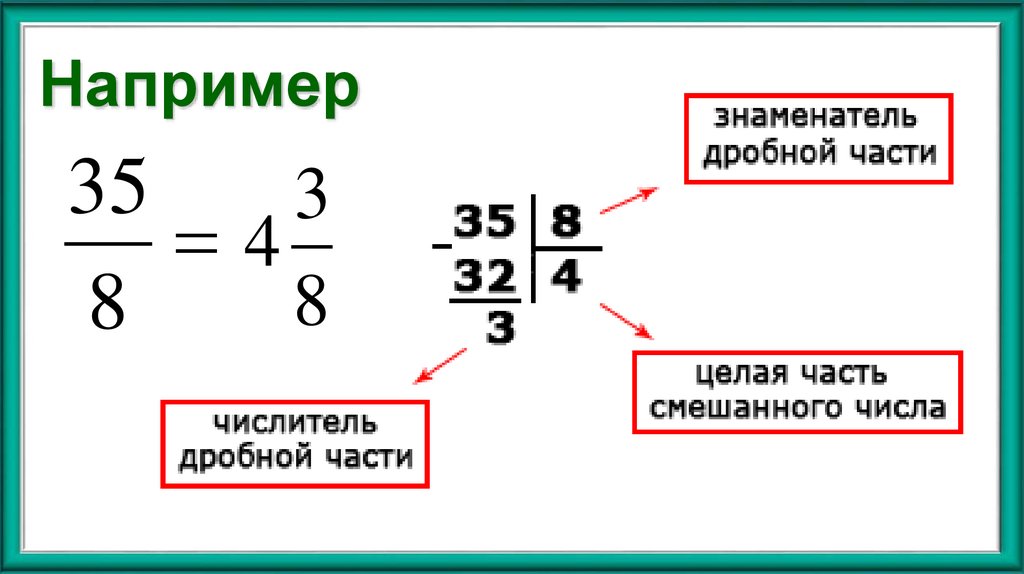
16. Например
17.
18. 4). Сложение и вычитание дробей с одинаковыми знаменателями
а). Правило сложениядробей
а b a b
с c
c
Например.
19. 4). Сложение и вычитание дробей с одинаковыми знаменателями
б). Правило вычитаниядробей
a b a b
c c
c
Например.
20. Запомним
а b a bс c
c
a b a b
c c
c
21. Вычислите
22. 5). Умножение и деление дробей
а). Правило умножениядробей
а b a b
с d c d
Например.
23. 5). Умножение и деление дробей (6 кл)
б). Правило делениядробей
a b a d a d
:
c d c b c b
Например.
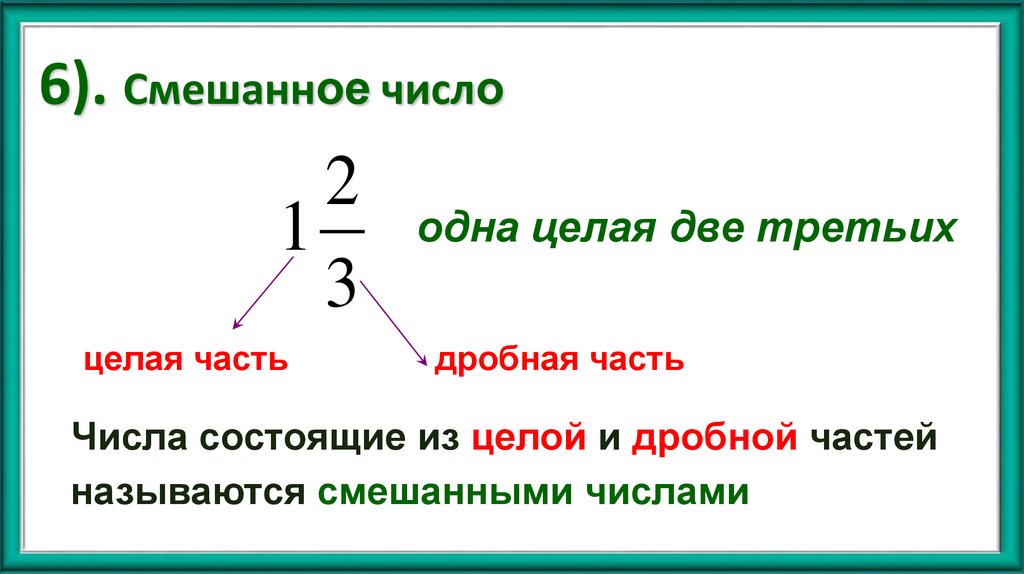
24. 6). Смешанное число
21
3
целая часть
одна целая две третьих
дробная часть
Числа состоящие из целой и дробной частей
называются смешанными числами
25. Рассмотрим где находятся смешанных числа на координатном (числовом) луче?
26. 7).
Например.27. Например
28. Сами
29. 8).
30. Например
353
4
8
8
31. Сами
32. Запомним
33. 9). Сложение и вычитание смешанных чисел
а). ПРИ СЛОЖЕНИИсмешанных чисел
целые части
СКЛАДЫВАЮТ
отдельно, а дробные отдельно
Например.
34. 9). Сложение и вычитание смешанных чисел
б). ПРИ ВЫЧИТАНИИсмешанных чисел
целые части
ВЫЧИТАЮТ отдельно,
а дробные - отдельно
Например.
35. 9). При вычитании смешанных чисел бывают случаи
а). Как вычесть дробь из единицы36. 9). При вычитании смешанных чисел бывают случаи
б). Как вычесть дробь из целого числа?37. 9). При вычитании смешанных чисел бывают случаи
в). Как вычесть, если дробная частьуменьшаемого меньше дробной части
вычитаемого?
38. 9). При вычитании смешанных чисел бывают случаи
39. Проверить решение
40. Выполните действия самостоятельно
41.
42.
21.12.1643.
44.
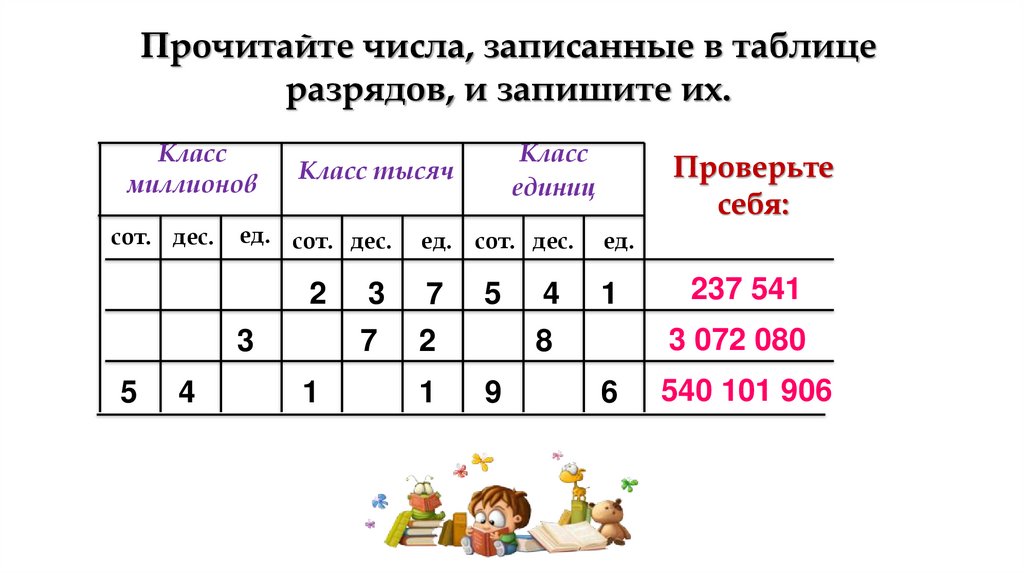
Прочитайте числа, записанные в таблицеразрядов, и запишите их.
Класс
миллионов
сот. дес.
Класс тысяч
ед. сот. дес.
2
3
5
4
Класс
единиц
1
Проверьте
себя:
ед. сот. дес.
ед.
5
1
3
7
7
2
1
4
3 072 080
8
9
237 541
6
540 101 906
45. тысячные
Какменяется
положение
единицы
в каждой
следующей
строке
Какое
арифметическое
действие
этому
Прочитайте
числа,
записанные
всоответствует
таблице
разрядов
.
Как
меняется
величина
соответствующего
числа?
по сравнению с предыдущей?
изменению?
А Целая
можно ли и
единицу
уменьшить
в10
раз?
Дробная
часть
часть
Класс
миллионов
Класс тысяч Класс единиц
Вывод:
сот. дес. ед. сот. дес. ед. сот. дес. ед.
1
д
е
с
я
т
ы
е
с
о
т
ы
е
т
ы
ся
ч
н
ы
е
д т
е ы с ыт
с ся т ся
я чн очн
т ые ые
и
м
и
л
л
и
о
н
н
ы
е
1 000 000
1
перемещая
единциу на один разряд
100 000
1
10 000
вправо, мы
каждый
раз
уменьшали
1
1 000
1
100
соответствующее
число
в
10
раз
и
1
10
1
делали это, пока
не дошли 1до
1
1
10
1
последнего разряда – разряда
единиц.
1
100
1
1
1000
46.
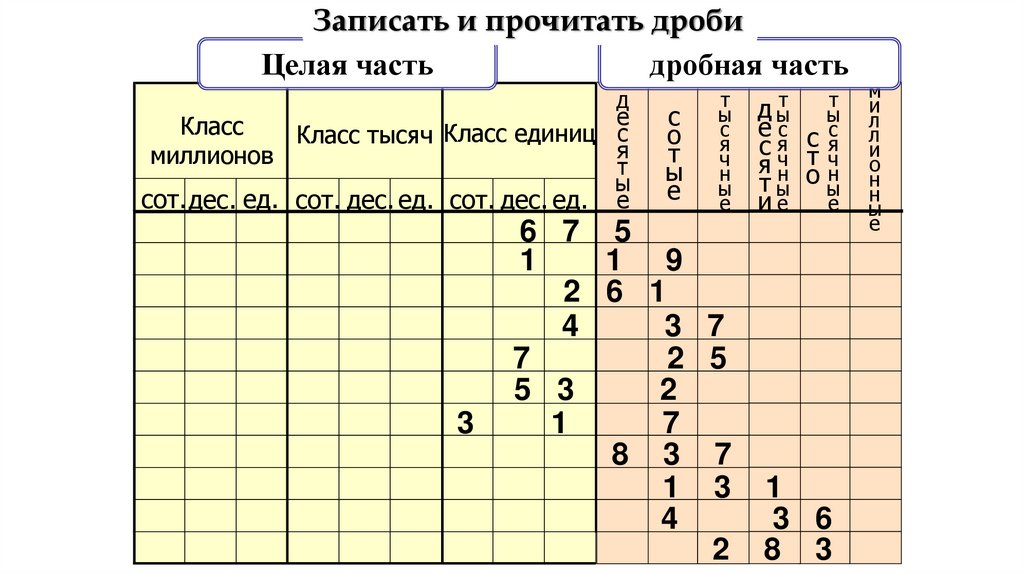
Записать и прочитать дробидробная часть
Целая часть
д
е
Класс
Класс тысяч Класс единиц с
я
миллионов
т
ы
сот. дес. ед. сот. дес. ед. сот. дес. ед. е
3
с
о
т
ы
е
6 7 5
1
1 9
2 6 1
4
3
7
2
5 3
2
1
7
8 3
1
4
т
ы
с
я
ч
н
ы
е
д ыт
ес
с чя
ян
ты
ие
т
ы
с яс
тч
н
оы
е
7
5
7
3
2
1
3 6
8 3
м
и
л
л
и
о
н
н
ы
е
47.
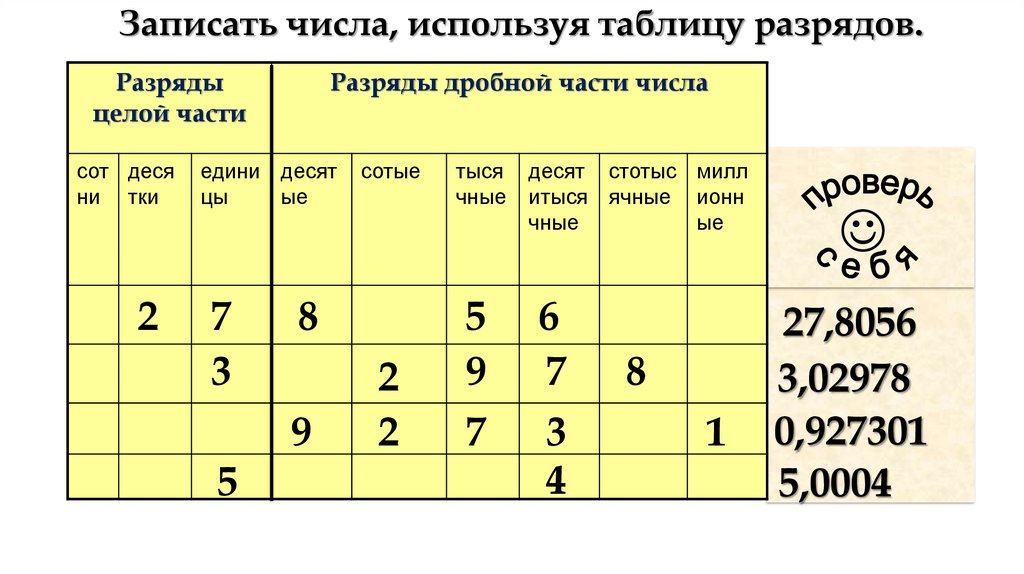
Записать числа, используя таблицу разрядов.Разряды
целой части
сот деся
ни тки
2
Разряды дробной части числа
едини десят
цы
ые
7
3
8
9
5
сотые
2
2
тыся
чные
десят стотыс милл
итыся ячные ионн
чные
ые
5
9
7
6
7
3
4
8
1
27,8056
3,02978
0,927301
5,0004
48.
Чтобы не ошибиться при переходе от десятичнойдроби к обыкновенной и наоборот, полезно помнить:
В десятичной дроби после запятой
должно быть столько же цифр, сколько
нулей в знаменателе соответствующей
ей обыкновенной дроби.
49.
Какие из дробей можно представить ввиде десятичных
Как понять, можно ли записать
обыкновенную дробь в виде
десятичной?
50.
Записать в виде десятичной дроби:Записать в виде обыкновенной дроби или
смешанного числа:
51.
Сравнение десятичныхдробей.
Сравним числа 37,634 и 37,628.
Сравнить числа: 6,27 и 6,2499.
Цифры в разрядах десятков,
единиц и десятых долей у них
одинаковые.
Уравняем число знаков после
запятой (припишем к дроби 6,27
два нуля получим 6,2700).
Смотрим на разряд сотых.
У первого числа разряд сотых
долей больше, значит, и оно само
больше:
37,634>37,628.
Сравниваем дроби с
одинаковым числом знаков
после запятой: 6,2700 и 6,2499.
6,2700>6,2499.
.
52.
СРАВНИТЕ ЧИСЛА:
5,38 и 5,29;
0,73 и 0,76;
23,514 и 24,279;
16,737 и 9,859;
137,3589 и137,3598.
ПРОВЕРЬ!
1) > 2) < 3) < 4) <
5) <.
Сравните.
5,83 и 5,8298:
15,8 и 15,79959:
0,795 и0,78598:
3,132 и 3,2;
57 и57,39;
982,1 и 983,09;
5,709 и 5,71.
53. Сложение и вычитание дробей
• Правило:Сложение и вычитание
осуществляется по
разрядам, начиная с
младших разрядов(запятая
должна находится под
запятой)
5,17
+ 2,5
7,67
7,72
-2,8
4,92
46,0
- 5,4
40,6
54.
Ученик выполнил действия и записал ответ, забывпоставить запятые. Исправьте его ошибку.
84,365+4,731=89096;
28,01- 9,51=1846;
3,1297+0,0854=32151;
510,666- 343,366=167300;
5,7893- 1,5685=4,2108;
0,37517+0,92318=129835.
55.
Правильно ли выполнены действия?Если не правильно, то объясните, в чем ошибка?
3,26
+ 2,5
3,51;
2,72
- 1,3
25,9;
3,26
+ 2, 5
5,31;
2,72
- 1, 3
1,6 9;
2,72
- 1,3
1 ,42.
3,26
+ 2,5
5,75;
2,72
- 1,3
2,59
3,26
+ 2,5
3,51;
56.
Самостоятельная работа.• Напишите по порядку 5 чисел, первое из которых равно
8,7, а каждое следующее на 0,5 больше предыдущего.
•Напишите по порядку 5 чисел, первое из которых 9,75, а
каждое следующее на 0,5 меньше предыдущего.
•Дополните:
•до единицы числа: 0.7; 0,03; 0,52; 0,006:
•до десяти числа: 2,3, 7,84; 6,05; 9,99:
•до ста числа: 47,34; 53,4; 29,13; 63,09.
57. Умножение дробей
Правило:
1.
Перемножить натуральные числа, не
обращая внимание на запятые;
Подсчитать сколько десятичных
знаков в каждом из множителей;
В полученном произведении отделить
справа столько знаков, сколько их в
обоих множителях.
2.
3.
3,2
* 2,5
160
+64
8,00
32*25=800
3,2(1знак)
2,5(1знак)
800(2знака)
3,2*2,5=8
8,00
58. Деление дробей
Правило:
1.
В делителе перенести
запятую в конец;
В делимом перенести
запятую на столько
знаков, сколько их в
делителе;
Выполнить деление
2.
3.
5,62:0,2 =56,2:2=28,1
9,702:2,31=970,2:231=4,2
59. Самостоятельная работа
• Вычисли:45,6:0,2
7,068:1,24
• Товарный поезд имеет длину в
1км и движется со скоростью 50
км/ч.За какое время он пройдет
туннель длиной 1км?
• Восстановите цифры:
977,6:3,?5=3??,8



















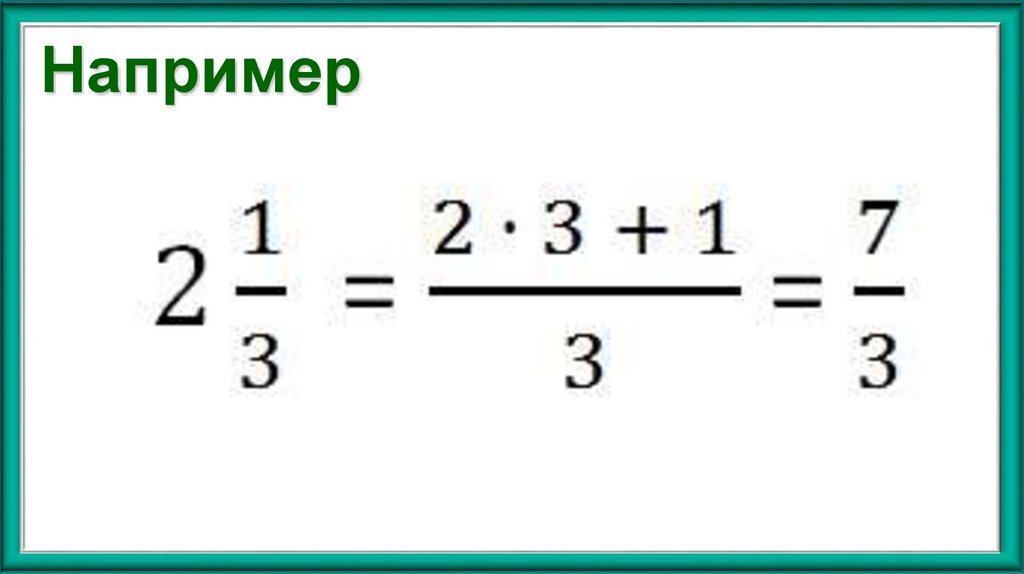



























 mathematics
mathematics








