Similar presentations:
Статистическое изучение динамики
1. Статистическое изучение динамики
1.Динамические ряды: их виды,правила построения и исследования.
2. Показатели анализа рядов
динамики. Средние показатели в
рядах динамики
3. Методы выравнивания рядов
динамики и выявления тенденции
ряда.
4. Индексы в оценке динамики и
взаимосвязей. Стандартизация.
2. Ряды динамики (хронологические, временные) -
Ряды динамики (хронологические,временные) ряды изменяющихся во времени
значений статистических показателей
расположенных в хронологическом
порядке.
Составными элементами рядов динамики
являются:
- цифровые значения изучаемого
показателя - уровни ряда динамики (У);
- периоды (или моменты) времени, к
которым они относятся (t).
3. Уровень ряда динамики –
это размер (величина, объем) того илииного явления или процесса,
достигнутый за определенный период
или к определенному моменту.
Элементами времени могут быть:
- моменты (начало, конец года, квартала,
месяца и т.п.) времени –моментный ряд
- периоды (год, квартал, месяц, сутки и
т.п.) времени – интервальный ряд
4. Интервал -
ИнтервалВ моментном ряду динамики– это
промежуток времени между
датами учета сведений
В интервальном ряду – тот же
промежуток времени, за который
обобщены приводимые сведения,
когда они накапливались.
5. Виды рядов динамики
в зависимости от способа выражения уровнейряды динамики ( абсолютных и производных
показателей)
в зависимости от характера приводимых
показателей (моментные и интервальные ряды
динамики)
в зависимости от расстояния между уровнями
(полные и неполные)
в зависимости от числа показателей
(изолированные и комплексные)
в зависимости от наличия основной тенденции
изучаемого процесса (стационарные и
нестационарные )
6. При составлении ряда динамики :
проводят периодизацию развитияявления
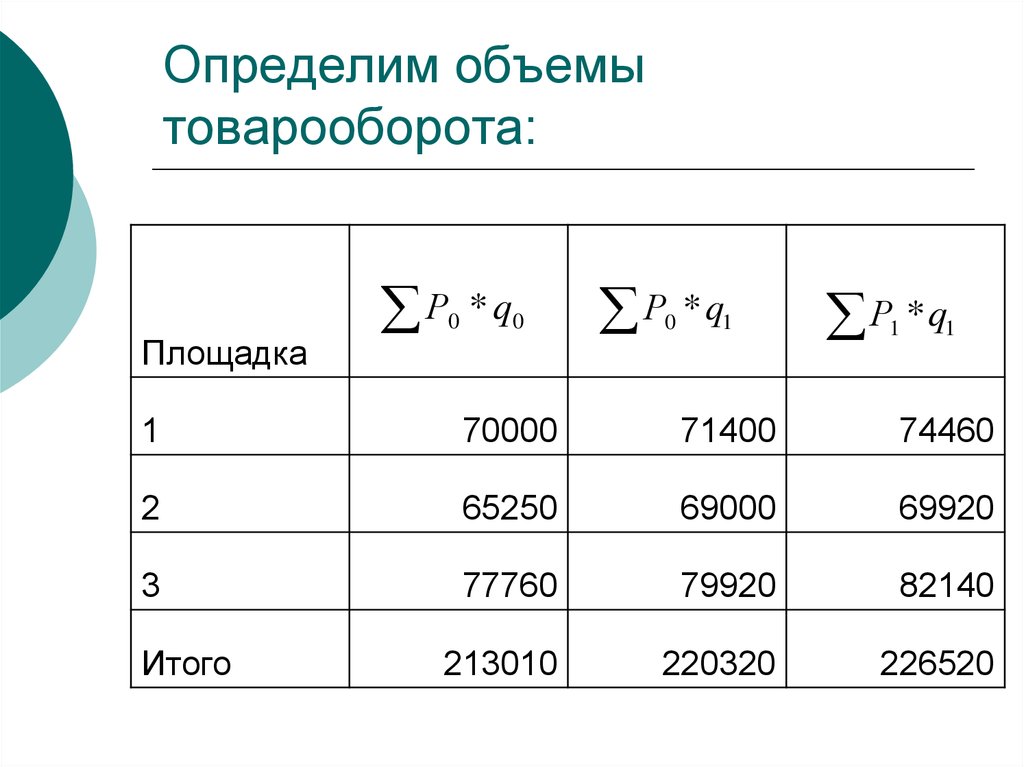
приводят к сопоставимому виду (по
территории, кругу охватываемых
объектов, единицам измерения,
времени регистрации, ценам,
методологии расчета)
решают вопрос о величине временных
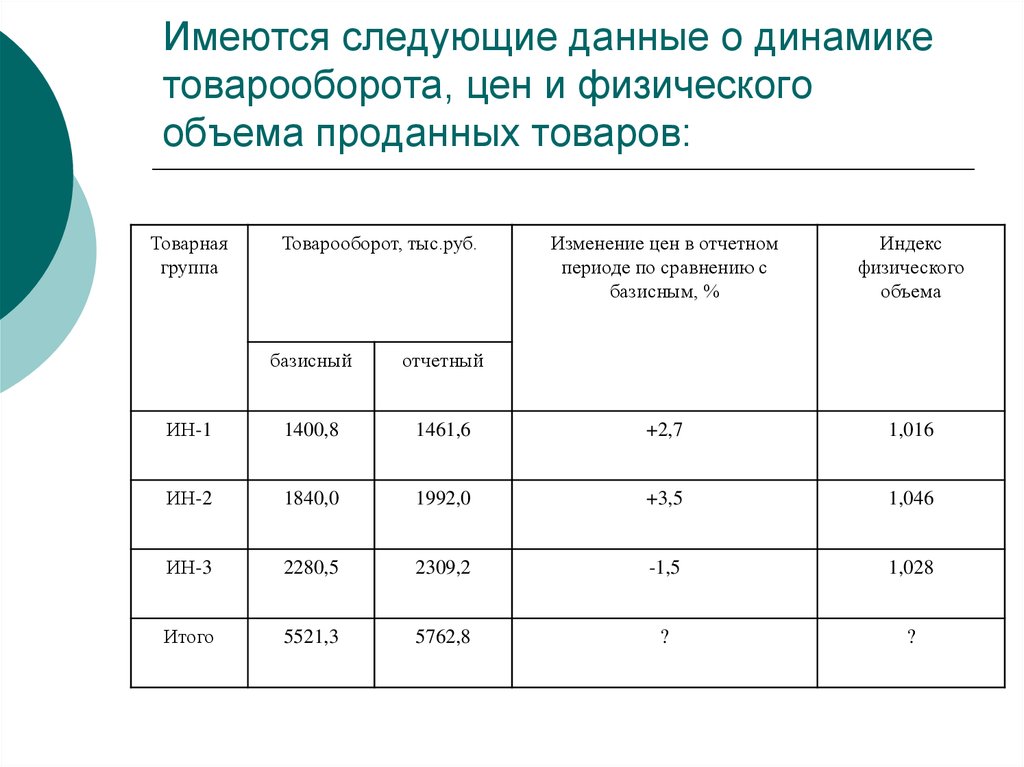
интервалов
упорядочивают уровни рядов динамики
во времени
7. Периодизация может осуществляться несколькими методами:
Исторический методМетод параллельной
периодизации
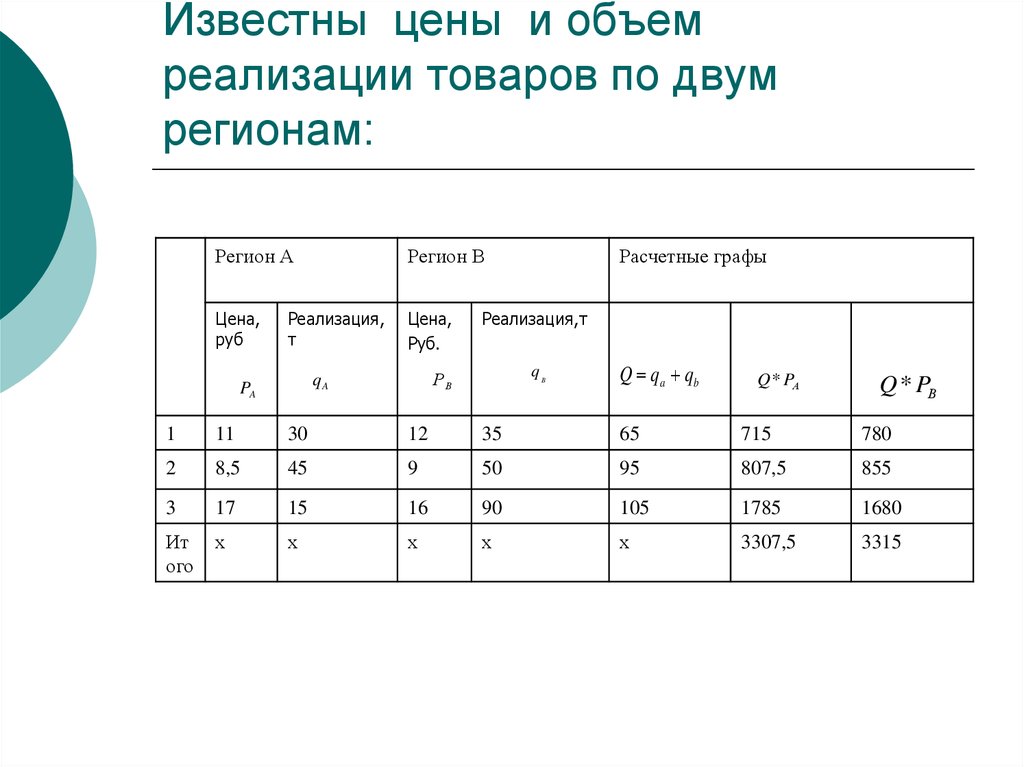
Методы многомерного
статистического анализа
8. Анализа рядов динамики позволяет:
— дать представление об изменениях показателейза прошедший период;
— охарактеризовать интенсивность отдельных
изменений;
— определить средние показатели временного
ряда;
— выявить основные тенденции и закономерности
изменений изучаемого явления;
— выявить факторы, обусловливающие
изменение явления во времени;
— осуществить прогноз о возможном уровне
явления на перспективу
9. Показатели анализа рядов динамики
абсолютный приросттемп роста
темп прироста
абсолютное значение одного процента
прироста
Система средних показателей динамики:
средний уровень ряда,
средние показатели анализа рядов
динамики
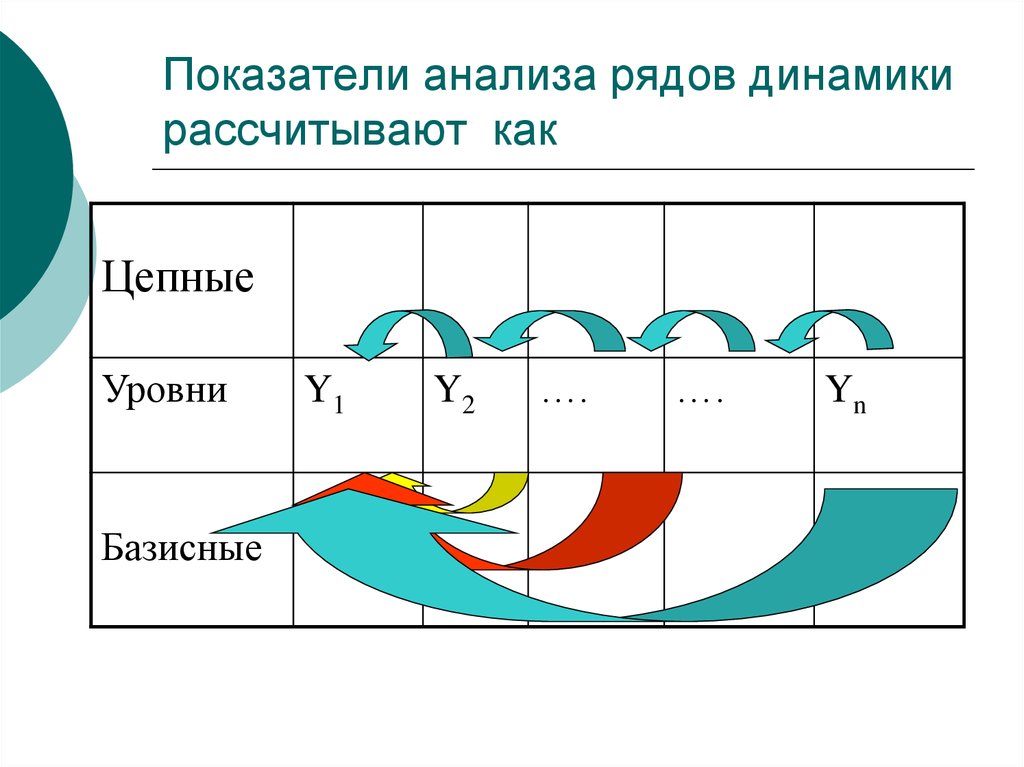
10. Показатели анализа рядов динамики рассчитывают как
ЦепныеУровни
Базисные
Y1
Y2
….
….
Yn
11. Абсолютный прирост
-Цепной:
iцеп =Yi—Yi-1
Базисный: iб
=Yi—Y1
Средний:
на основе цепных абсолютных
приростов:
цеп i
-
k
на основе базисного абсолютного
прироста:
баз
п 1
12. Коэффициент роста:
Цепной:Базисный:
Среднегодовой:
или
К р Yi : Yi 1
К р Yп : Y1
К р k ПК р цеп
Yn
К р n 1
Y1
п 1 ПК р цеп
13. Темпы роста :
Тр =Кр *100Темп прироста:
Тпр =Тр -100
Среднегодовой темп роста и
прироста: Т К *100
р
р
Т пр Т р 100
14. Абсолютное содержание 1% прироста:
Yi Yi 1А
Tp 100
Или
А= Yi-1 :100
15. Средний уровень ряда динамики:
Моментного:0.5Y1 Y2 Y3 .... 0.5Yn
Y
n 1
Интервального:
Y
Yi
n
Yt
Y
t
i i
i
16. При анализе социально-экономических явлений во времени выявляют три компонента динамики:
- основные тенденциями, которыевыражают, как правило,
долговременные изменения (тренд);
- систематические и кратковременные
изменения (сезонные колебания);
- несистематические случайные
колебания, которые часто обусловлены
субъективными и иными частными
причинами
17. Тренд —
это долговременная компонента рядадинамики, выражающая длительную,
ведущую тенденцию развития явления
Изучение тенденции ряда включает
два основных этапа:
ряд динамики проверяется на наличие
тренда;
производится выравнивание
временного ряда и непосредственное
выделение тренда с экстраполяцией
полученных результатов
18. Проверка на наличие тренда в ряду динамики может быть осуществлена:
- методом средних величин;- фазочастотным критерием знаков
первой разности (Валлиса и
Мура);
- критерием Кокса и Стюарта.
- методом серий
19. Выделение тренда проводят:
1.2.
3.
Способом укрупнения
интервалов
Методом скользящей средней
Методом аналитического
выравнивания
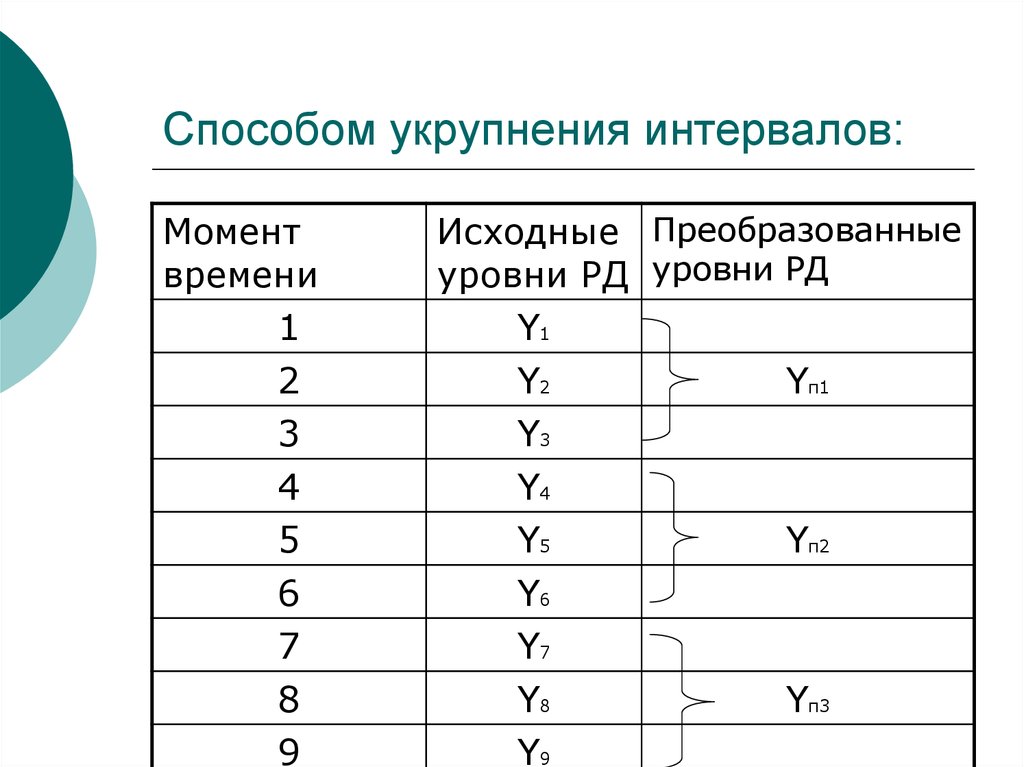
20. Способом укрупнения интервалов:
Моментвремени
1
2
3
4
5
6
7
8
9
Исходные Преобразованные
уровни РД уровни РД
Y1
Y2
Yп1
Y3
Y4
Y5
Yп2
Y6
Y7
Y8
Yп3
Y9
21. Методом скользящей средней:
временя1
2
3
4
5
6
7
8
Исходные Преобразованные
уровни РД уровни РД
Y1
Y2
Yп1
Y3
Yп2
Y4
Yп3
Y5
Yп4
Y6
Y7
Y8
Yп5
Yп6
Yп7
22. При аналитическом выравнивании используются следующие зависимости:
-линейная:
f (t ) а0 а1t
- параболическая:
-
f (t ) а 0 а1t a 2 t 2
экспоненциальные:
f (t ) ехр(а 0 а1t a 2 t )
2
23. Для оценки параметров (а0, а1, а2,...) используют:
метод наименьших квадратов,который обеспечивает
наименьшую сумму квадратов
отклонений фактических уровней
от выровненных:
min (Yi f (t ))
2
24. Yt=a0+a1tt.
Yt - значения выравненногоряда, которые необходимо
вычислить;
t - показатель времени (месяцы,
годы, и т.д.);
а0, и a1 - параметры прямой,
определенные из системы
нормальных уравнений:
25. система нормальных уравнений:
а0 * n а1 t Ya0 t a1 t 2 Y * t
26. Оценку надежности уравнения регрессии проводят на основе
критерия Фишера (F) - при этомфактический уровень (Fфакт)
сравнивается с теоретическим (F
табличным) значением:
Fфакт
2
ост
2
факт
(n k )
2
ост
(k 1)
2
(
Y
f
(
t
))
n
2
2
факт
Y2 ост
2
(
f
(
t
)
Y
)
n
27. Проанализируем динамику числа обращений в отдел социальной защиты по одному из районов области:
база 2007Число
обращений
,тыс.
2008
2009
2010
2011
40,2
37,0
33,6
33,1
32,5
Абсолютный
Цеп.
-
-3,2
-3,4
-0,5
-0,6
прирост
базис
-
-3,2
-6,6
-7,1
-7,7
Коэффициент
Цеп.
-
0,921
0,908
0,985
0,982
роста
базис
-
0,921
0,836
0,823
0,808
Темп роста
Цеп.
-
92,1
90,8
98,5
98,2
базис
-
92,1
83,6
82,3
80,8
Цеп.
-
-7,9
-9,2
-1,5
-1,8
базис
-
-7,9
-16,4
-17,7
-19,2
-
0,402
0,370
0,336
0,331
Темп прироста
Абс.содер- е %
прироста
28. Среднегодовые показатели динамики:
Средний абсолютный прирост:по базисным - (-7,7)/4=-1,9 (тыс. ) или
по цепным - (-3,2-3,4-0,5-0,6)/4=-1,9(тыс.)
Средний коэффициент роста:
по базисным -
К р 4 32,5 / 40,2 4 0,808 0,948
по цепным – К р 4 0,92 * 0,908 * 0,985 * 0,982 4 0,808 0,948
Средний темп роста:
Т р К р *100 0,948 *100 94,8(%)
Средний темп прироста: Т
пр
Т р 100 94,8 100 5,2(%)
29. Средний уровень ряда динамики:
определяем по формуле средней арифметическойпростой (ряд интервальный):
У1 У 2 .... У n 1 У n
У
n
(40,2 37 33,6 33,1 32,5) / 5
176,4 / 5 35,3 (тыс.)
30. Среднегодовые показатели ряда динамики используют для прогноза:
а) прибавляя последовательно к последнему уровню ряда динамикисреднегодовой абсолютный прирост
Yn t Yn * t
Yn+t - - экстраполируемый уровень ряда динамики,
n+t - номер этого уровня (года);
n - номер конечного уровня (года) периода, за который рассчитан
среднегодовой абсолютный прирост
t - срок прогноза (период упреждения)
Таким образом, ожидаемое число обращенийй через два года составит:
32,5+ 2*(-1,9)=28,7 (тыс. человек)
31. На основе относительных показателей (Кр):
б) умножая уровень ряда динамики на среднегодовойкоэффициент роста столько раз, на сколько лет мы
прогнозируем уровень ряда динамики:
Yn t Yn * К
t
р
ожидаемое число обращений населения через два года
составит:
32,5*0,948*0,948= 29,2 (тыс.человек).
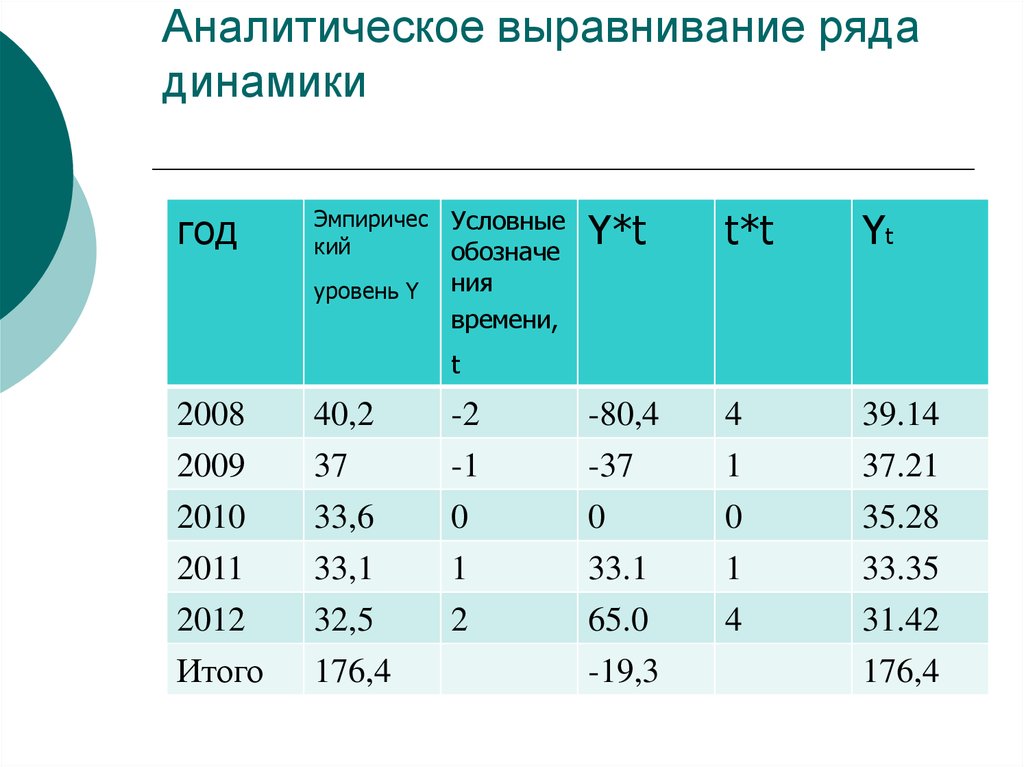
32. Аналитическое выравнивание ряда динамики
годЭмпиричес Условные
кий
обозначе
уровень Y
Y*t
t*t
Yt
ния
времени,
t
2008
2009
40,2
37
-2
-1
-80,4
-37
4
1
39.14
37.21
2010
2011
33,6
33,1
0
1
0
33.1
0
1
35.28
33.35
2012
32,5
2
65.0
4
31.42
Итого
176,4
-19,3
176,4
33. Параметры и уравнение тренда:
из первого уравнения системы определяют а0 –среднийn
уровень ряда динамики:
1 У i
а0
176,4 : 5 35,28
n
из второго уравнения системы определяем а1:
а1
Yt 19,3 :10 0,193
t
2
уравнение тренда: Yt=35,28-1,93t,
через два года (t=4) ожидается, что число обращений в
районе составит: 35,28-1,93*4=27,56 (тыс.)
34. Сезонные колебания -
Сезонные колебанияколебание уровней ряда
динамики, возникающие под
влиянием смены времени года
Сезонные колебания строго
цикличны – повторяются строго
через год (квартал, месяц,
неделя, день, часы в сутках), хотя
сама длительность года имеет
колебания
35. Уровень сезонности оценивается с помощью:
1)индексов сезонности:
I t .сез
I t сез
Yt
Y
или
i
t сез
Т
2) метода гармонического анализа
36. Индексы сезонности:
Если тренда нет или он незначителен, то длякаждого месяца (квартала) его рассчитывают по
Y
формуле:
I i сез t
Yср
где Yt – средний уровень показателя за месяц
(квартал t);
Yср - общий средний уровень показателя
Если тенденция имеется, то сначала проводят
аналитическое выравнивание, а затем
рассчитывают индекс сезонности по формуле:
I i сез
Yt
Y
где Y -выровненный уровень
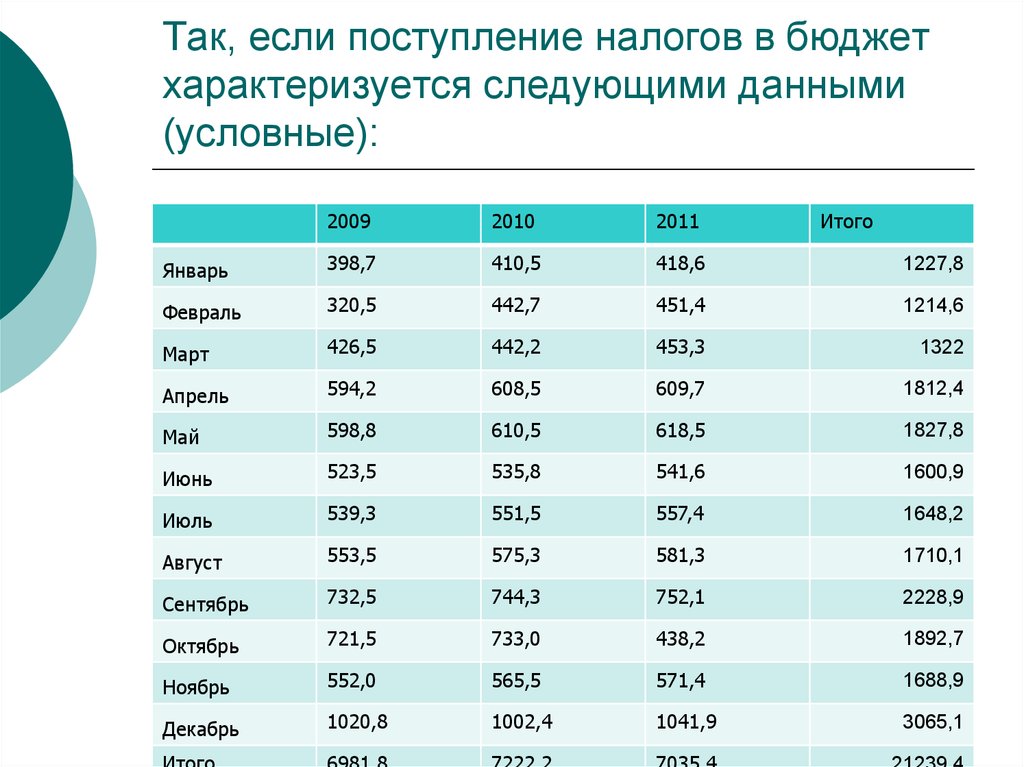
37. Так, если поступление налогов в бюджет характеризуется следующими данными (условные):
20092010
2011
Итого
Январь
398,7
410,5
418,6
1227,8
Февраль
320,5
442,7
451,4
1214,6
Март
426,5
442,2
453,3
1322
Апрель
594,2
608,5
609,7
1812,4
Май
598,8
610,5
618,5
1827,8
Июнь
523,5
535,8
541,6
1600,9
Июль
539,3
551,5
557,4
1648,2
Август
553,5
575,3
581,3
1710,1
Сентябрь
732,5
744,3
752,1
2228,9
Октябрь
721,5
733,0
438,2
1892,7
Ноябрь
552,0
565,5
571,4
1688,9
Декабрь
1020,8
1002,4
1041,9
3065,1
38. Таблица по расчету индексов сезонности
Сумма за 3 годаЯнварь
Февраль
Март
Апрель
Май
Июнь
Июль
Август
Сентябрь
Октябрь
Ноябрь
Декабрь
Средний уровень
Индекс сезонности
1227,8
409,3
0,693692
1214,6
404,9
0,686234
1322
440,7
0,746914
1812,4
604,1
1,023984
1827,8
609,3
1,032685
1600,9
533,6
0,904489
1648,2
549,4
0,931213
1710,1
570,0
0,966186
2228,9
743,0
1,259301
1892,7
630,9
1,069352
1688,9
563,0
0,954208
3065,1
1021,7
1,731744
39. Последовательность расчета индекса сезонности
определяем средний размер поступлений налоговза каждый месяц:
так, в январе (398,7+410,5+418,6):3=1227,8:3=409,3
определяем средний размер поступлений налогов в
среднем за период:
(6981,8+7222,2+7035,2):36=21239,4:36=590,0
Индекс сезонности:
409,3:590,0=0,694 (т.е. в январе поступило налогов
69,4% от среднемесячного уровня
40. Гармонический анализ
выполняют представляя временной ряд как суммупериодических колебательных процессов
T /2
Yt f (t )
n 1
2
an cos nt
T
2
bn sin nt
T
где Yt фактический уровень ряда в момент
(интервал) времени t
f (t) - выровненный уровень или трендовое
значение ряда в тот же момент (интервал) времени
an , bn - параметры колебательного процесса
(гармоники) с номером
41. Индекс –
относительная величина,показывающая, во сколько раз
уровень изучаемого явления в
данных условиях отличается от
уровня того же явления в
других условиях.
42. Различие условий может проявляться
-во времени (индексы динамики)-в пространстве (территориальные
индексы)
-в выборе в качестве базы сравнения
какого-либо условного уровня
(например, структуру той или иной
группы населения –
стандартизованные индексы,
планового уровня –индексы
планового задания, выполнения
плана)
43. Различают:
Индивидуальные индексыОбщие (агрегатные) индексы
Индексы средних величин
Средние из индивидуальных
(средний арифметический,
средний гармонический)
Территориальные индексы
44. Индивидуальные индексы-
Индивидуальные индексыотносительная величина, получаемая присравнении уровней, например,
iQ Q1 / Q0 , гдеQ qp
- товарооборота:
iq q1 / q0
- Физ-го объема товарооборота:
i р Р1 / Р0
- цен на товары:
- Причем, iQ i p * i q
где i – обозначение индивидуального индекса
q. p- индексируемые величины
1 и 0 –обозначение уровней отчетного и
базисного периода соответственно
45. Общие (агрегатные) индексы
Относительные величины в видесравнения агрегатов (сумм
произведений взвешивающего
показателя на объемный Q = р ∙
q ), например, индекс общего
объема товарооборота в
агрегатной форме:
IQ
p
p
1
q1
0
q0
.
46. Соответственно, общие индексы-
Соответственно, общиеиндексы
Цен- соотношение товарооборота
отчетного периода с товарооборотом
отчетного периода в сопоставимых ценах
(базисного периода):
p q
Ip
p
1
1
0
q1
.
Физического объема- соотношение
товарооборота отчетного периода в
сопоставимых ценах с товарооборотом
базисного периода:
Iq
p
p
0
q1
0
q0
.
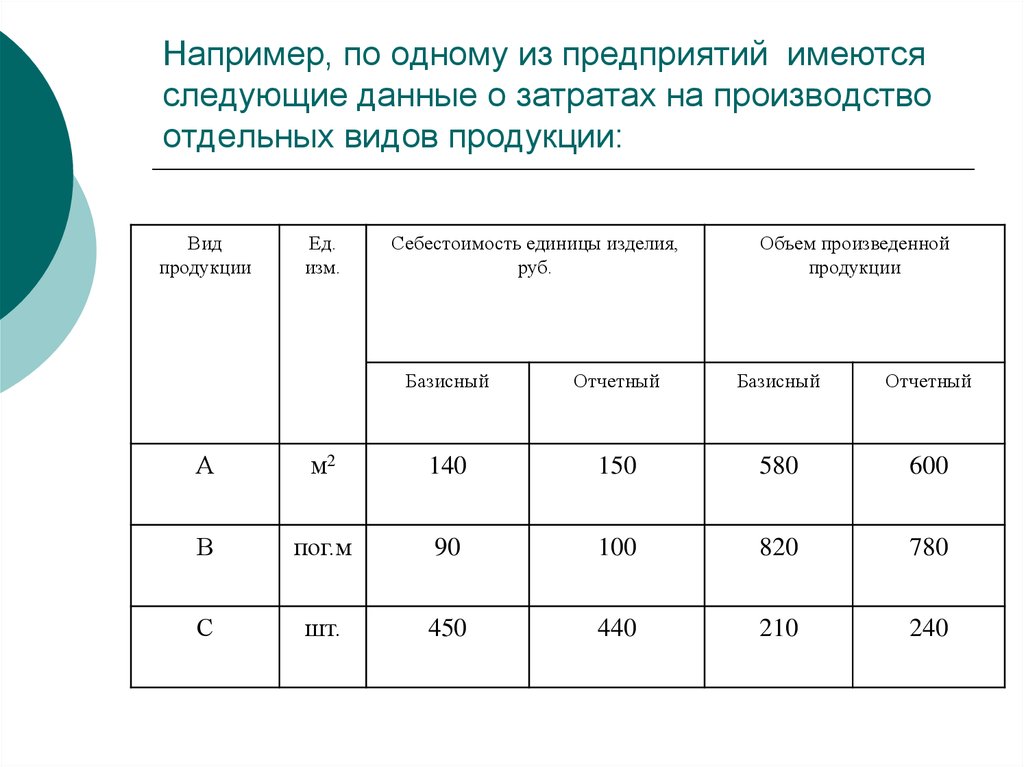
47. Например, по одному из предприятий имеются следующие данные о затратах на производство отдельных видов продукции:
Видпродукции
Ед.
изм.
Себестоимость единицы изделия,
руб.
Объем произведенной
продукции
Базисный
Отчетный
Базисный
Отчетный
А
м2
140
150
580
600
В
пог.м
90
100
820
780
С
шт.
450
440
210
240
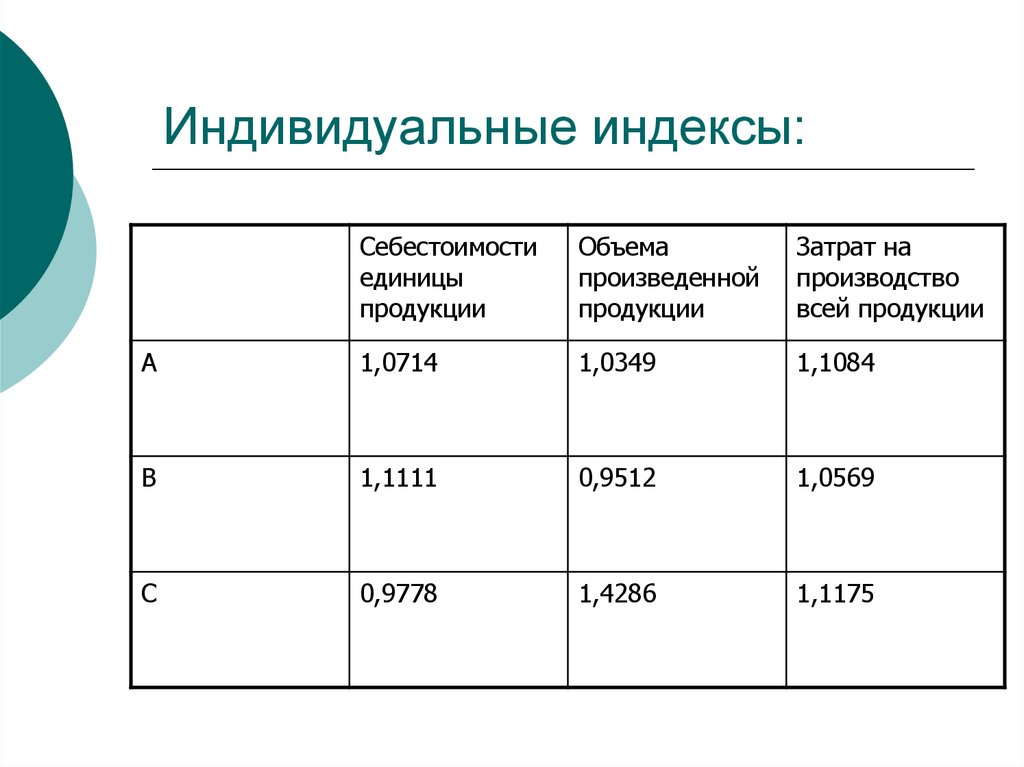
48. Индивидуальные индексы:
Себестоимостиединицы
продукции
Объема
произведенной
продукции
Затрат на
производство
всей продукции
А
1,0714
1,0349
1,1084
В
1,1111
0,9512
1,0569
С
0,9778
1,4286
1,1175
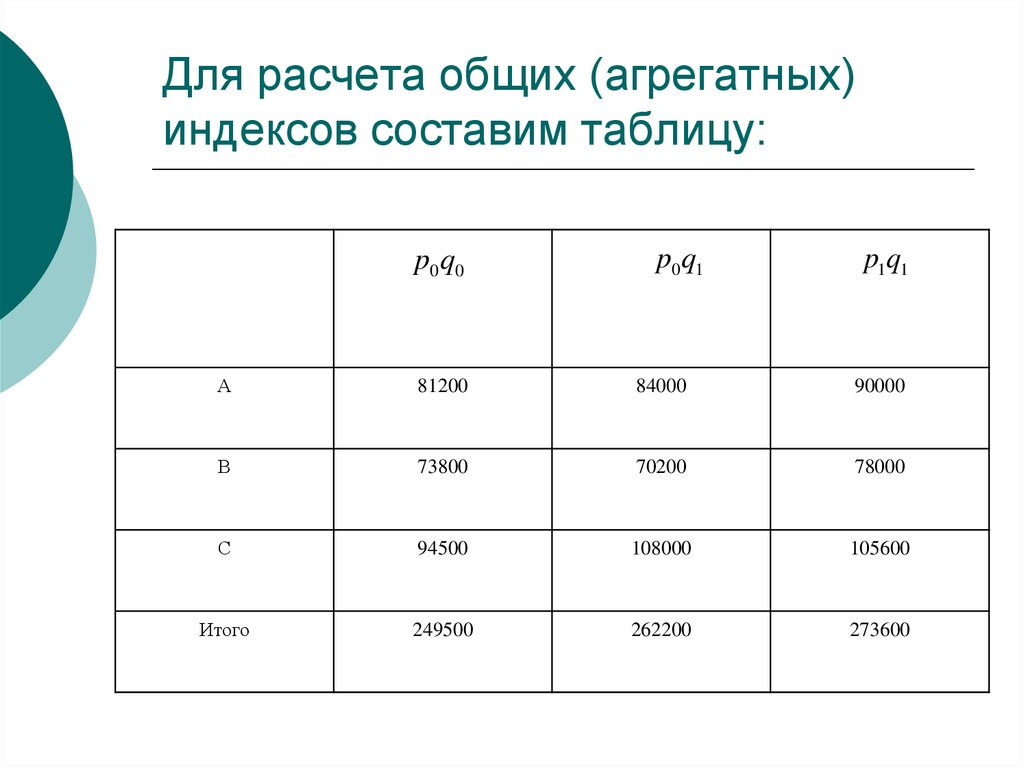
49. Для расчета общих (агрегатных) индексов составим таблицу:
p0 q0p0 q1
p1q1
А
81200
84000
90000
В
73800
70200
78000
С
94500
108000
105600
Итого
249500
262200
273600
50. Агрегатные индексы:
Затрат:I рq
Iр
Iq
р q
р q
1
1
0
0
273600
1,0966 или 109,7%( 9,7%)
249500
Себестоимости единицы продукции:
р q
р q
1
1
0
1
273600
1,0435 или 104,3 ( 4,3%).
262200
Физического объема продукции:
р q
р q
0
1
0
0
262200
1,0509 или105,1 (5,1%).
249500
51. Разностное сравнение числителя и знаменателя индексов показывает прирост затрат:
Общей суммы:на 273600 - 249500 = 24100 рублей
вследствие изменения
себестоимости единицы продукции:
на 273600-262200=11400 ( рублей )
вследствие изменения физического
объема:
на 262200-249500=12700 ( рублей )
24100=11400+12700
52. Индексы средних величин
индекс переменного состава отношение двух средних величин(учитывает одновременно и
структурные изменения в составе
совокупности, и изменение уровня
качественного признака у отдельных
объектов): р q
р q
Iя
q
1
1
1
:
q
0
0
0
53. индекс постоянного (или фиксированного) состава
Агрегатный индекс, полученный по типуиндекса цен (фондоотдачи,
себестоимости единицы продукции и
т.п.) - отражает изменение среднего
уровня качественного показателя под
влиянием изменения самого
качественного показателя у отдельных
единиц совокупности:
I пост
р q р q
:
q
q
1
1
1
0
1
1
54. Индекс структурных изменений
I стрр q р q
:
q
q
0
1
1
0
0
0
рd
р d
0 1
0
0
где do – удельные веса, доли предприятий в общем
объеме выпускаемой продукции в базисном периоде,
d1 – удельные веса или доли каждого предприятия в
общем объеме выпускаемой продукции в отчетном
периоде:
do = q0 / q0,
d1 = q1 / q1.
Между индексом переменного состава, постоянного
состава и структурных сдвигов существует
соотношение
Iпер.сост = Iстр *Iпост.сос
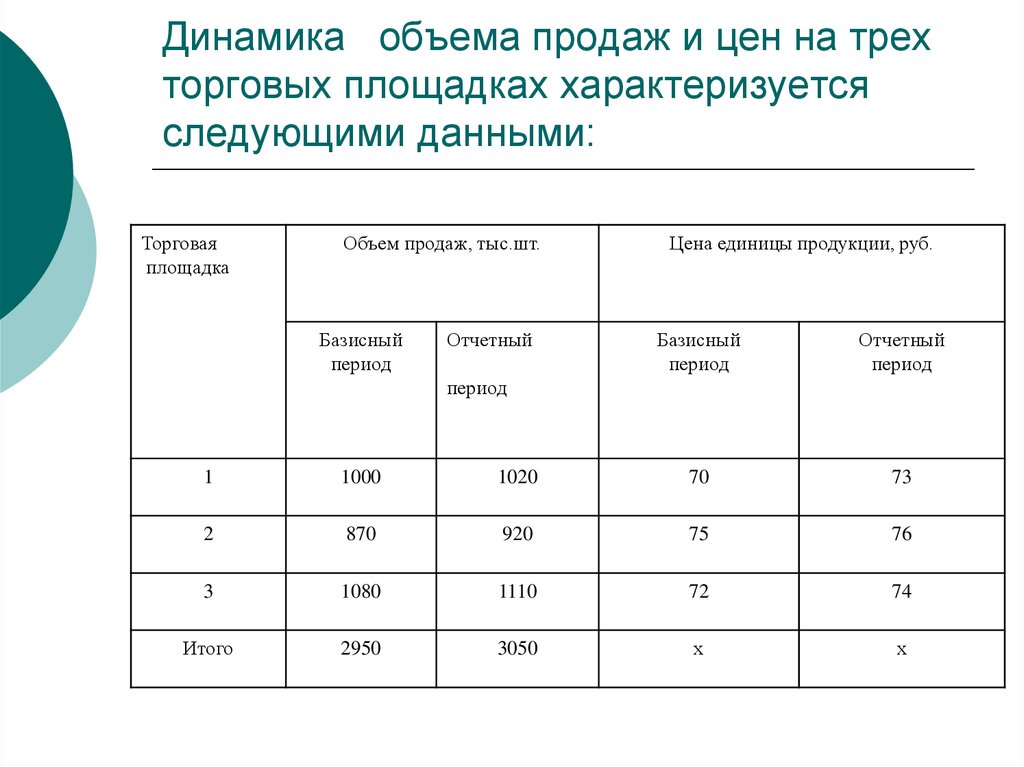
55. Динамика объема продаж и цен на трех торговых площадках характеризуется следующими данными:
Торговаяплощадка
Объем продаж, тыс.шт.
Базисный
период
Отчетный
Цена единицы продукции, руб.
Базисный
период
Отчетный
период
период
1
1000
1020
70
73
2
870
920
75
76
3
1080
1110
72
74
Итого
2950
3050
х
х
56. Определим объемы товарооборота:
Р0
Площадка
* q0
Р *q
0
1
Р *q
1
1
1
70000
71400
74460
2
65250
69000
69920
3
77760
79920
82140
213010
220320
226520
Итого
57. Индексы
IяПеременного состава:
р q : р q
q
q
1
1
0
1
0
226520 213010
:
74,26 : 72,21 1,028
3050
2950
Постоянного состава:
I пост
р q : р q
q
q
1
1
1
0
0
0
0
226520 219040
:
74,26 : 71,82 1,034
3050
3050
Структурных сдвигов:
I стр
р q : р q
q
q
0
1
1
0
0
0
71,82 : 72,21 0,995
58. Индексы общего объема товарооборота может быть рассчитан как индекс средний из индивидуальных
по форме среднего арифметическогоиндекса:
IQ
p
p
1
q1
0
q0
i p
p
p
0
iq q0
0
q0
i i p
p q
p
q
0
0
0
q0
i p q
p q
Q
0
0
0
по форме средней гармонической
величины
IQ
p
p
1
q1
0
q0
p
p
1
1
q1
i p q1 iq
0
p q
p q i
1
1
1
1
Q
59. Индекс физического объема товарооборота может быть рассчитан как индекс средний из индивидуальных
по форме среднего арифметическогоиндекса:
Iq
p q p i q
p q p q
0
1
0
0
0
q
0
0
0
i p q
p q
q
0
0
0
0
60. Индекс цен рассчитывают как индекс средний из индивидуальных
по форме средней гармоническойвеличины:
Iр
p q
p q
p q p q i
1
1
0
1
1
1
1
1
p
61. Имеются следующие данные о динамике товарооборота, цен и физического объема проданных товаров:
Товарнаягруппа
Товарооборот, тыс.руб.
Изменение цен в отчетном
периоде по сравнению с
базисным, %
Индекс
физического
объема
базисный
отчетный
ИН-1
1400,8
1461,6
+2,7
1,016
ИН-2
1840,0
1992,0
+3,5
1,046
ИН-3
2280,5
2309,2
-1,5
1,028
Итого
5521,3
5762,8
?
?
62. Индекс товарооборота может быть определен по формуле
Агрегатного индекса:p q 1461,6 1992,0 2309,2 5762,8 1,044
I
p q 1400,8 1840,0 2280,5 5521,3
среднего арифметического индекса:
1
1
0
0
Q
IQ
i i p q
p q
p
q
0
0
1400,8 *1,027 *1,016 1840,0 *1,035 *1,046 2280,5 * 0,985 *1,028
5762,8 / 5521,3 1,044
1400,8 1840,0 2280,5
средней гармонического индекса:
IQ
0
0
1461.6 1992.0 2309.2
p q
5762.8 : 5521,3 1,044
p q / iQ 1461.6 /(1.027 *1.016) 1992.0 /(1.035 *1.046) 2309.2 /(0.985 *1.028)
1
1
1
1
объем продаж в фактически действовавших ценах увеличился на
4,4% или на 241,5 тыс.руб
63. Индексы изменения общей суммы товарооборотав связи с изменением
физического объема:p0 q1 iq p0 q0 1400,8 *1,016 1840,0 *1,046 2280,5 *1,028 5692,21
Iq
1,031
1400,8 1840,0 2280,5
5521,30
p0 q0 p0 q0
Iр
в связи с изменением цен:
p
p
1
q1
0
q1
p q
pq
i
1
1
1 1
p
1461,6 1992,0 2309,2 5762,8
1,012
1461,6 1992,0 2309,2 5692,2
1,027
1,035
0,985
1,044=1,031*1,012
64. Территориальные индексы -
Территориальные индексы это разновидность относительныхвеличин сравнения, когда
сопоставляются сложные
показатели, относящиеся к
одному и тому же периоду
времени, но к разным
территориям (городам, районам,
областям, государствам).
65. Построение территориальных индексов
товарооборота – это отношениесуммы выручки от продажи в
одном из районов к аналогичному
показателю в другом. Один из
районов (например, “В”) берется
за базу сравнения, т.е.
I a, А В
p
p
A
qA
В
qВ
66. Территориальные индексы
физического объематоварооборота
p q
I p, А В
цен
p q
I p, А В
A
В
p
p
A
q
В
q
где р – средняя межрайонная цена товара каждого вида,
q– суммарный по двум районам объем продаж каждого
вида товара.
67. Известны цены и объем реализации товаров по двум регионам:
Регион АРегион В
Цена,
руб
Цена,
Руб.
Реализация,
т
Реализация,т
qВ
РВ
qA
PA
Расчетные графы
Q q a qb
Q * PА
Q * PВ
1
11
30
12
35
65
715
780
2
8,5
45
9
50
95
807,5
855
3
17
15
16
90
105
1785
1680
Ит
ого
х
х
х
х
х
3307,5
3315
68. Территориальные индексы
РР
В
qВ
А
А
12 * 35 9 * 50 16 * 90
2310
2,39
товарооборота:
q
11* 30 8,5 * 45 17 *15 967,5
p q 3315,0 : 3307,5 1,002
I
цен:
p q
IВ/ А
A
p, А Б
Б
Цены в регионе В на 0,2% превышают цены региона А.
физического объема:
для его определения
необходимо рассчитать средние цены по каждому товару:
Р1 =(11,0*30+12,0*35)/65=11,54; Р2 8,76 Р3 16,1
I q, А Б
p q
p q
В
А
11,54 * 35 8,76 * 50 16,1* 90 2290,9
2,33
11,54 * 30 8,76 * 45 16,1*15 981,9

























































 economics
economics








