Презентация_С_математика_9 клас

1.

співбесіда з математики

2.

Абітурієнту необхідно мати:
2 кулькові сині ручки, олівець,
лінійку
Забороняється користуватися:
калькулятором, мобільним
телефоном, будь-якими іншими
джерелами інформації.

3.

Завдання співбесіди
складаються з двох частин
Перша частина
Друга частина містить
містить 6 завдань
2 завдання, розв'язок
тестової форми. Для
яких має
кожного із завдань
супроводжуватися
запропоновано чотири
обґрунтуванням
варіанти відповіді,
серед яких тільки один
правильний

4.

Завдання з вибором відповіді вважається
виконаним правильно, якщо вступник у відповіді
записує букву, якою позначена правильна
відповідь.
Якщо абітурієнт в тестовому завданні позначив
правильну відповідь, то він отримує десять (10)
балів; якщо неправильна відповідь виправлена
на правильну – п’ять (5) балів.
Максимальна кількість балів, яку вступник
може отримати за виконання першої частини
екзаменаційного білету, дорівнює шістдесят (60)
балів.

5.

Друга частина передбачає два завдання
оцінювання кожного у 20 балів за критеріями:
- завдання виконано в повному обсязі – 20
балів;
- завдання
виконано
з
незначними
арифметичними помилками – 1-19 балів;
- завдання виконано неправильно – 0 балів.
Максимальна кількість балів за виконання
другої частини співбесіди, дорівнює сорок (40)
балів.
Отже, правильне розв’язання 6 завдань першої
частини
та
2
завдань
другої
частини
екзаменаційного білету дає можливість отримати
максимальну оцінку 200 балів.

6.

А Б В Г
Місце для
розв’язання
завдань ІІ частини

7.

ВЛАСТИВОСТІ СТЕПЕНЯ
m
n
a a =
m+n
a
m
n
m-n
a :a = a
m
n
(а ) = mn
а
n
n
n
(ab) = a b

8. Формули скороченого множення

(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
a2-b2 = (a+b)(a-b)

9.

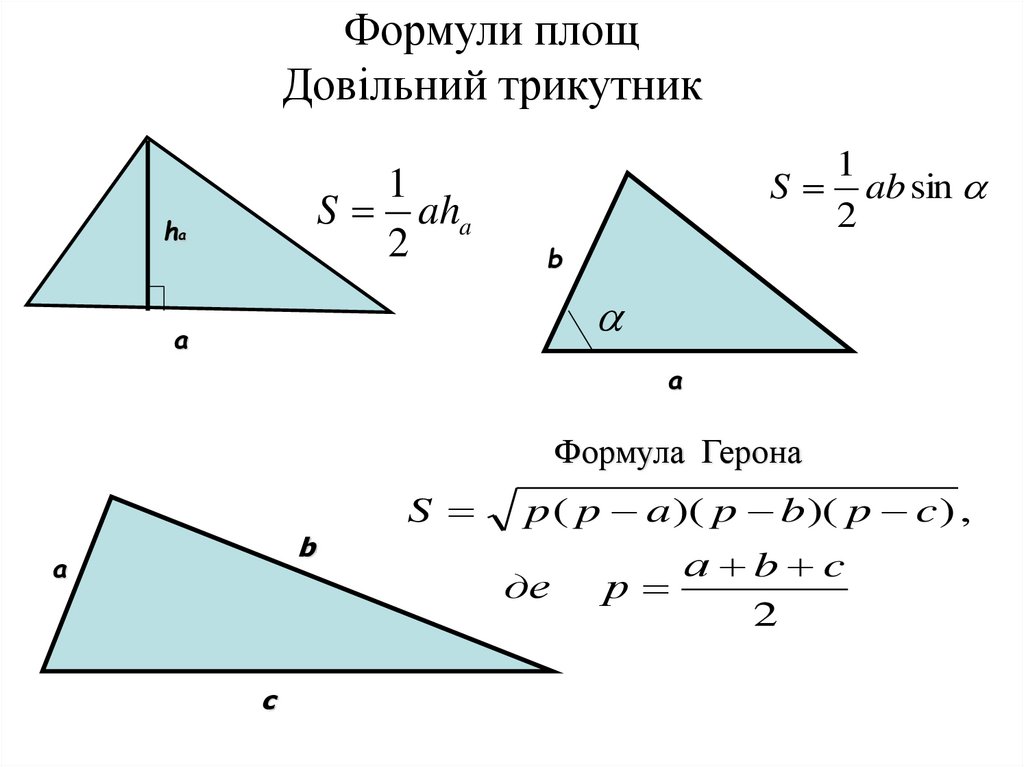
Формули площ
Довільний трикутник
1
S aha
2
ha
1
S ab sin
2
b
a
a
Формула Герона
S
p ( p a )( p b)( p c ) ,
b
a
де
c
а b c
р
2

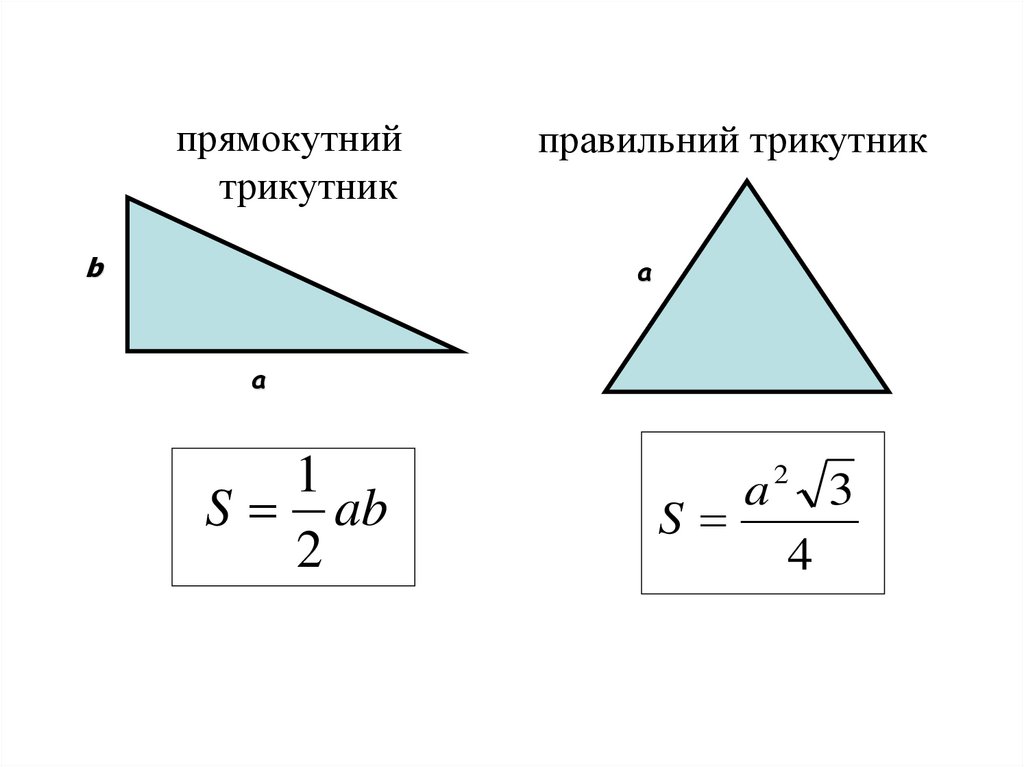
10.

прямокутний
трикутник
b
правильний трикутник
a
a
1
S ab
2
S
a
2
4
3

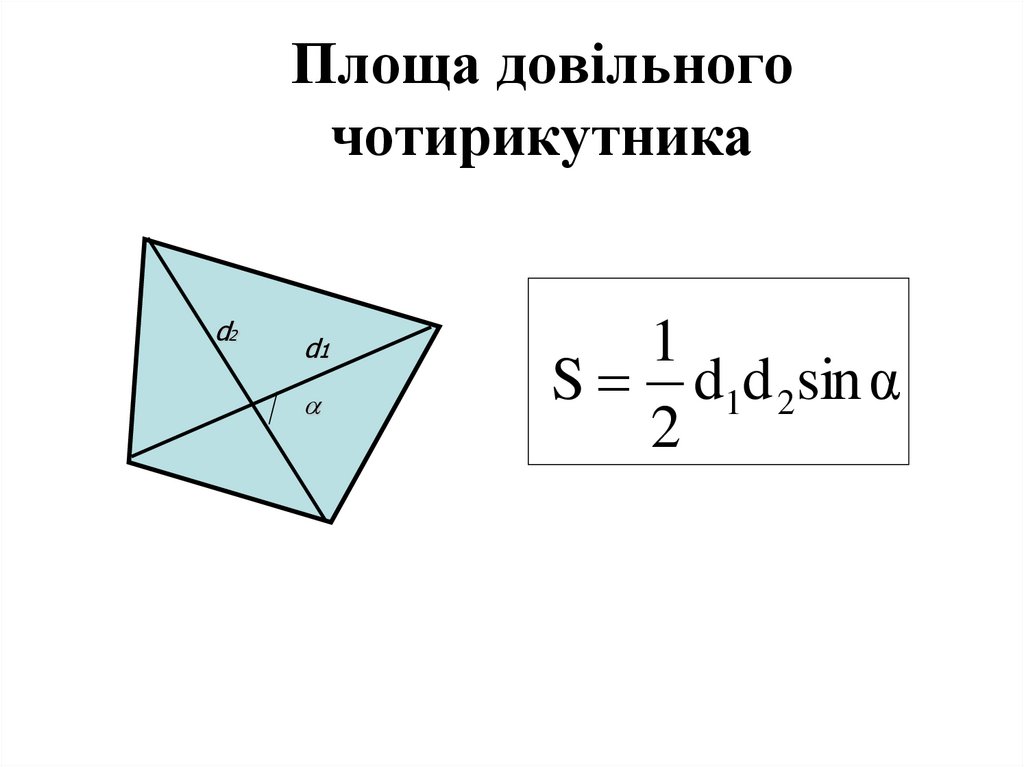
11. Площа довільного чотирикутника

d2
d1
1
S d1d 2sin α
2

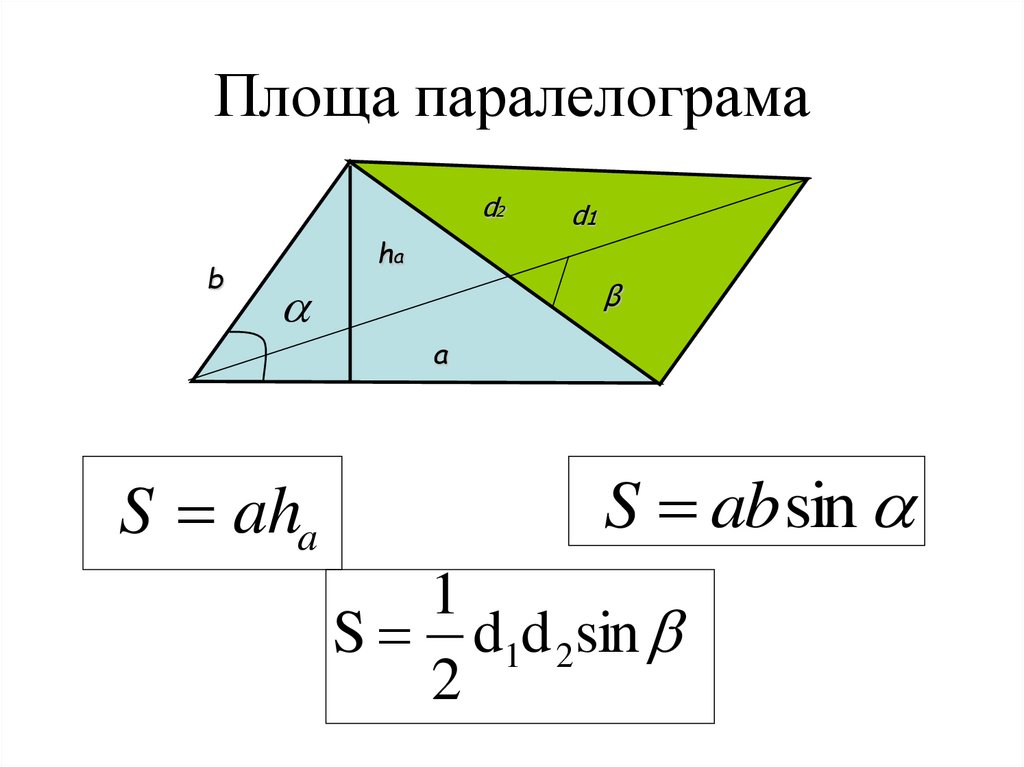
12. Площа паралелограма

d2
b
d1
ha
β
a
S aha
S ab sin
1
S d1d 2sin
2

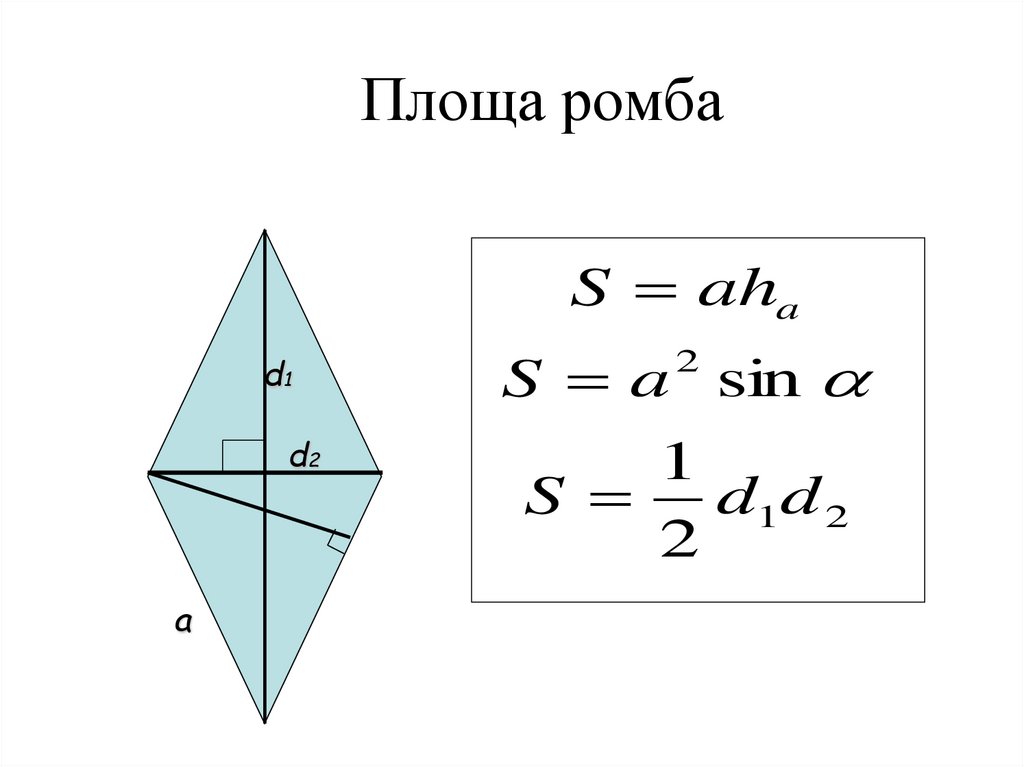
13. Площа ромба

S aha
d1
d2
а
S a sin
1
S d1d 2
2
2

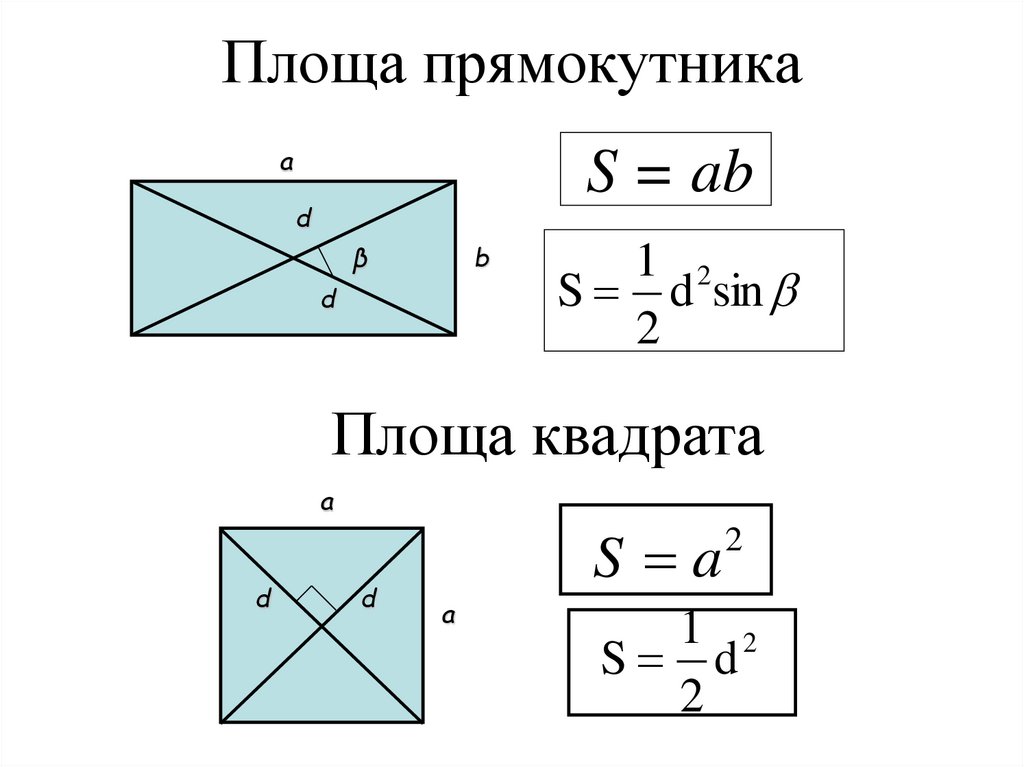
14. Площа прямокутника

a
S = ab
d
b
β
d
1 2
S d sin
2
Площа квадрата
a
d
d
S a
a
2
1 2
S d
2

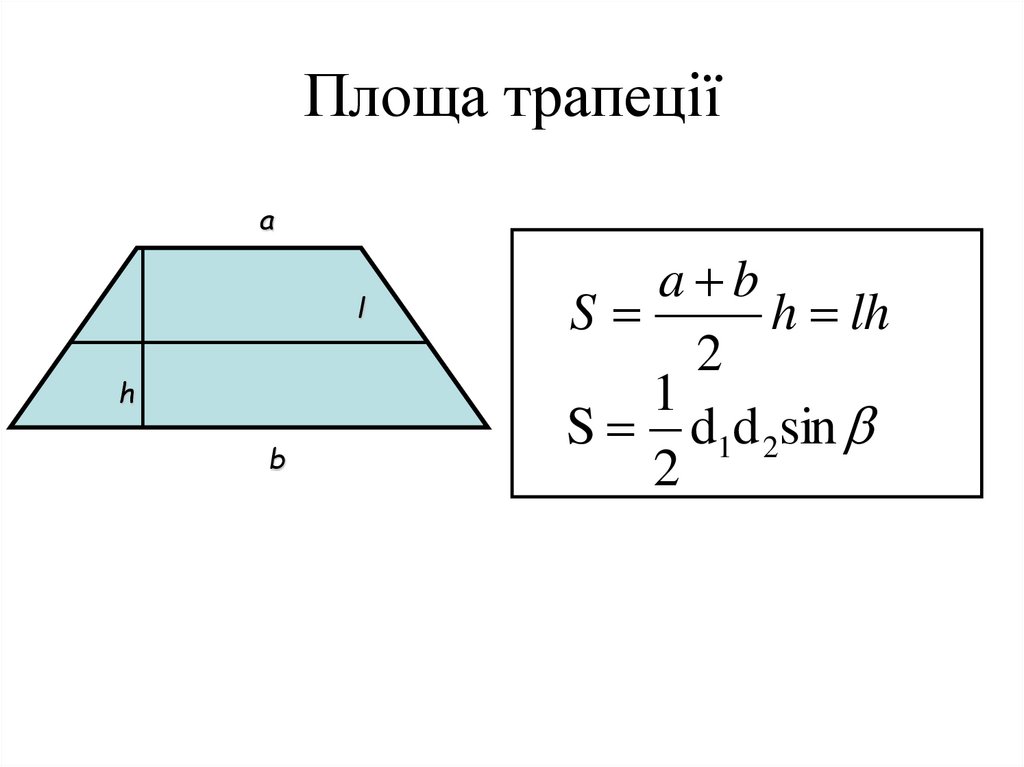
15. Площа трапеції

a
l
h
b
a b
S
h lh
2
1
S d1d 2sin
2

16. Зразок завдань з математики:

Виконайте завдання, обравши один правильний, на Вашу думку, варіант відповіді.
1. Обчисліть значення виразу (2,3 + 0,7) :
А)1;
Б) 12;
В) 9;
Г) 3.
2. Округліть число 19,254 з точністю до десятих.
А) 19,2;
Б) 19,25;
В) 19,3;
Г) 19,26.
3. Розв'яжіть нерівність –Зx ≥ 12 .
А)х ≥ –4;
Б)х ≥ 4;
В) х ≤ 4;
Г)х ≤ –4.
4. Скільки коренів має рівняння 2x2 – 5х + 4 = 0?
А) два корені; Б) один корінь; В) жодного кореня;
Г) безліч коренів.
5. Виконайте ділення:
А) n12;
Б) n2;
В) n8;
Г) n4
6. В рівнобічному трикутнику кут при основі дорівнює
бічними сторонами?
А) 70 ; Б) 110 ;
.
Чому дорівнює кут між
Г) 60 .
В) 145 ;
Таблиця для занесення відповідей на І частину екзаменаційної роботи
№ завдання
Правильна відповідь
Позначки вчителя
1
2
3
4
5
6

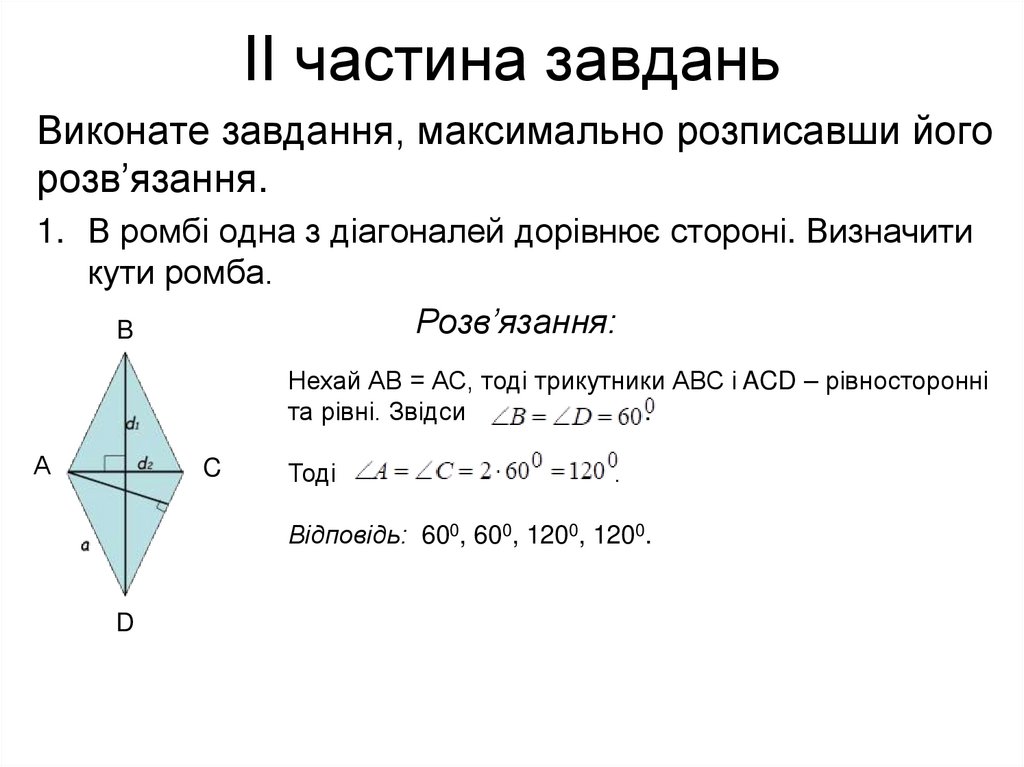
17. ІІ частина завдань

Виконате завдання, максимально розписавши його
розв’язання.
1. В ромбі одна з діагоналей дорівнює стороні. Визначити
кути ромба.
Розв’язання:
B
Нехай АВ = АС, тоді трикутники АВС і ACD – рівносторонні
та рівні. Звідси
.
А
C
Тоді
.
Відповідь: 600, 600, 1200, 1200.
D

18.

x 1 x2 2x 1
:
Подайте у вигляді дробу вираз
.
2
3x
9x
Розв’язання: